学习笔记:树与图上的计数问题
Prüfer 序列
\(n\) 个点的有标号无根树可以与一个长度为 \(n - 2\) 的 Prüfer 序列对应。
从树到 Prüfer 序列
- \(f\) 为空序列。
- 如果当前树上多于两个节点,假设当前标号最小的叶子为 \(x\),与 \(x\) 相连的节点标号为 \(y\),那么把 \(x\) 从树上删除,把 \(y\) 加入 \(f\) 末尾。
- 重复 2. 直到树上只有两个节点。
性质
- 在构造完 Prufer 序列后原树中会剩下两个节点,其中一个一定是编号最大的点 \(n\)。
- 每个节点在序列中出现的次数是其度数减 \(1\),因此没有出现的就是叶节点。
实现
可以 \(O(n)\) 实现这个转换。
由于最后一定会留下 \(n\),不妨钦定 \(n\) 为根(把 \(n\) 拎起来)。
定义:
- \(f_i\) 为 \(i\) 的父节点。
- \(d_i\) 为 \(i\) 的儿子数量。
- \(p_i\) 为 prufer 序列的第 \(i\) 项。
流程:
定义 \(i\) 表示当前编号最小的叶子的指针,\(cur\) 为当前序列填到哪一项。
- \(p_{cur} = f_i\)。
- 将 \(d_{p_{cur}}\) 减 \(1\),表示删去 \(i\) 这个节点。
- 如果 \(d_{p_{cur}} = 0\) 且 \(p_{cur} < i\),那么 \(p_{cur}\) 比当前最小值还要小,直接令 \(p_{cur + 1} = f_{p_{cur}}\) 。
void Tree_to_Prufer() {
for(int i = 1; i < n; ++ i) {
cin >> f[i];
++ d[f[i]];
}
for(int cur = 0, i = 1; cur < n - 2; ++ i) {
while(d[i]) ++ i;
p[++ cur] = f[i];
while(cur < n - 2 && -- d[p[cur]] == 0 && p[cur] < i) {
p[cur + 1] = f[p[cur]];
++ cur;
}
}
for(int i = 1; i <= n - 2; ++ i) cout << p[i] << ' ';
}
从 Prüfer 序列到树
- 找到当前不在 \(f\) 中且还未使用的最小元素 \(x\)。(等价于是叶子节点)
- \(x\) 与 \(f\) 的第一个元素连边。
- 删除 \(f\) 的第一个元素,如果 \(f\) 非空,重复上述过程。(把叶子删掉,当前节点度数减一)
- 最后还剩两个点未使用,将他们连边。
代码实现类似。
void Prufer_to_Tree() {
for(int i = 1; i <= n - 2; ++ i) {
cin >> p[i];
++ d[p[i]]; // 以 $n$ 为根,儿子数量
}
p[n - 1] = n;
for(int cur = 1, i = 1; cur <= n - 1; ++ cur, ++ i) {
while(d[i]) ++ i;
f[i] = p[cur];
while(cur < n - 1 && -- d[p[cur]] == 0 && p[cur] < i) {
f[p[cur]] = p[cur + 1];
++ cur;
}
}
for(int i = 1; i <= n - 1; ++ i) cout << f[i] << ' ';
}
Caylay 定理
\(n\) 个点的有标号无根树有 \(n^{n -2}\) 种。
例题
P6086 【模板】Prufer 序列
P2290 [HNOI2004] 树的计数
题意:给定每个点的度数 \(d_i\),求不同的有标号无根树个数。
相当于 \(d_i - 1\) 个 \(i\) 排进长为 \(n - 1\) 的序列的方案数。
即
由于保证了答案小于 \(10^{17}\),可以不用高精,全程用一个大于 \(10^{17}\) 的质数取模(如 \(\text{4179340454199820289}\))。
特判无解,根据 prufer 序列的性质,一定有 \(\sum d_i - 1 = n - 2\)。
CF1267F Foolpruf Security
题意:二分图 \(G\) 左部有 \(n\) 个节点,标号 \(1, 2, \cdots, n\),右部 \(m\) 个节点,标号 \(n + 1, n + 1, \cdots, n + m\)。
满足图 \(G\) 是一棵树。
给定其 prufer 序列的两个子序列 \(a, b\),其中 \(\forall a_i \le n\) 且 \(\forall b_i > n\),让你重构一张可能的图,或判无解。
prufer 序列最后剩下的两个点,一定一个在左边,一个在右边。
于是左边删了 \(m - 1\) 个点,则 prufer 序列中不大于 \(n\) 的元素被添加 \(m - 1\) 次。
同理,大于 \(n\) 的元素右 \(n - 1\) 个。
因此如果 \(|a| \ge m\) 或 \(|b| \ge n\),则判无解,否则如果长度不够,随便填满。
代码与模板类似,稍加改动使得左右端点分局两侧。
void Prufer_to_Tree() {
b[n] = n + m;
for(int ia = 1, ib = 1, j = 1; ia <= m - 1 || ib <= n; ++ j) {
while(d[j]) ++ j;
int cur;
if(j <= n) {
cout << j << ' ' << b[ib] << '\n';
cur = b[ib];
}
else {
cout << j << ' ' << a[ia] << '\n';
cur = a[ia];
}
while(1) {
if(cur <= n) {
if(ia <= m - 1 && -- d[a[ia]] == 0 && a[ia] < j) {
cout << a[ia] << ' ' << b[ib] << '\n';
++ ia;
cur = b[ib];
}
else break;
}
else {
if(ib <= n && -- d[b[ib]] == 0 && b[ib] < j) {
cout << b[ib] << ' ' << a[ia] << '\n';
++ ib;
cur = a[ia];
}
else break;
}
}
cur <= n ? ++ ia : ++ ib;
}
}
BZOJ4766 文艺计算姬
题意:完全二分图 \(K(n, m)\) 的生成树个数。
根据上题结论,将其 prufer 序列分为大于 \(n\) 和不大于 \(n\) 的两部分,长度分别为 \(n - 1\) 和 \(m - 1\)。
所以总方案为 \(m^{n - 1}n^{m - 1}\)。
E-Valuable Forests
题意:定义树 \(T\) 的权值 \(w(T) = \sum_{i = 1}^n\deg(i)^2\),森林 \(G\) 的权值为 \(\sum_{T\in G} w(T)\),求所有 \(n\) 元有标号森林的权值和。
定义 \(f(n)\) 表示不同 \(n\) 元森林个数。
枚举元素 \(n\) 所在树的大小,在剩下 \(n - 1\) 个元素里选 \(i - 1\) 个与 \(n\) 构成一棵树,这棵树有 \(i^{i - 2}\) 种形态。
定义 \(g(n)\) 表示不同 \(n\) 元树的权值和。
枚举每个点 \(i\) 的权值 \(d\),则贡献为满足恰有 \(d - 1\) 个位置是 \(i\) 的 prufer 序列个数。
定义 \(F(n)\) 为 \(n\) 元森林权值和。
枚举 \(n\) 所在树的大小 \(i\),\(g(i)\) 的贡献为 \(n - i\) 元森林数量,\(F(n - i)\) 贡献为 \(i^{i - 2}\)。
Matrix Tree Theorem
设无向图 \(G= (V, E), \ D = \text{diag}(d_1, d_2, \cdots, d_n)\),\(d_i\) 是 \(i\) 的度数,\(G\) 的拉普拉斯矩阵 \(L = D - E\),则 \(G\) 的生成树个数为 \(\det(L_0)\),其中 \(L_0\) 为 \(L\) 去掉第 \(i\) 行第 \(i\) 列(\(i\) 任取)。
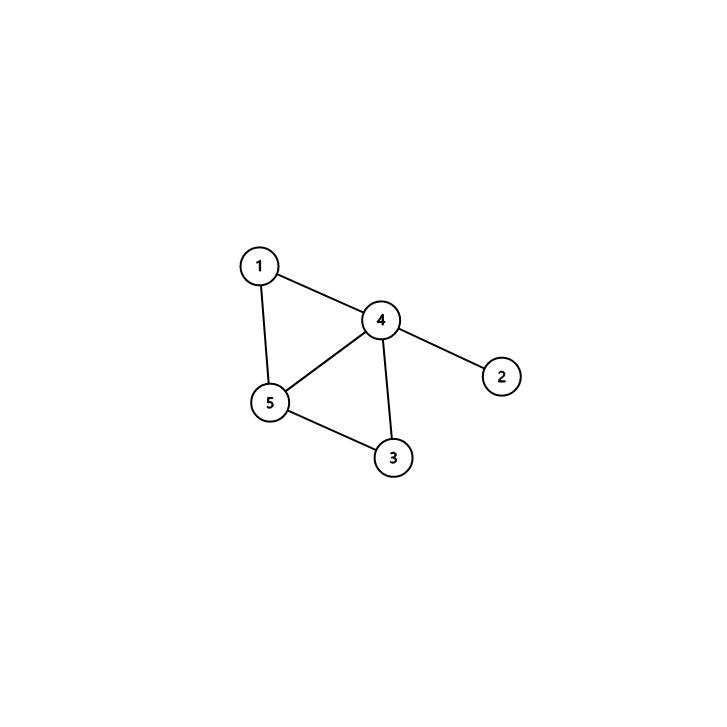
删去第 \(4\) 行第 \(4\) 列:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号