学习笔记：Burnside引理、Pólya定理

等价类

在计数问题中，需要明确计数的对象中哪些是视为相同的，哪些是不同的。我们可以在对象的集合上定义一种 等价关系，然后对 等价类 计数。

关系

对于一个集合 \(X\)，它的关系是集合 \(X\times X\) 的一个子集 \(R\)。如果对于 \(x, \ y \in X\)，有 \((x, y) \in R\)，我们称 \(x, \ y\) 有关系 \(R\)，记作 \(xRy\)。

1. \(\text{等于 }\subseteq \mathbb{R^2}, \ \text{等于 } = \{(x, y)\in \mathbb{R^2} \mid x = y\}\)。

   如果 \(x \text{等于} y\)，那么 \((x, y) \in \text{等于}, \ x = y\)。

2. \(\equiv_m\subseteq \mathbb Z^2, \ \equiv_m = \{(x, y) \in\mathbb Z^2\mid x = y + km\}\)。

   如果 \(x\equiv_my\)，那么 \((x, y) \in \equiv_m, \ x = y + km\)。

等价关系

如果关系 \(R\) 满足：

• 自反性：\(\forall x\in X, \ xRx\)。
• 对称性：\(\forall x, y \in X, \ xRy\Leftrightarrow yRx\)。
• 传递性：\(\forall x, y, z \in X, \ xRy\land yRz\Rightarrow xRz\)。

则称 \(R\) 是 \(X\) 上的一个等价关系。

等价类

假设关系 \(R\) 是 \(X\) 上的一个等价关系，对于 \(x\in X\)，令 \(\mathbf{x}_R = \{y \in X\mid xRy\}\)，则

• 如果 \(xRy\) 成立，那么 \(\mathbf x_R = \mathbf y_R\)（\(xRz \land xRy \Rightarrow yRz\)）。
• 如果 \(xRy\) 不成立，那么 \(\mathbf x_R \cap \mathbf y_R = \varnothing\)（\(xRz \land yRz \Rightarrow xRy\)）。

则称 \(\mathbf x_R\) 为代表元 \(x\) 的一个 \(R\) 等价类，所有 \(R\) 的等价类构成集合 \(X\) 的一个分划。

例：给一个 \(n\) 元环的节点涂上颜色，\(m\) 种颜色，通过旋转得到的方案算同一种方案，求方案数。

定义关系 \(R = \{\text{(方案一, 方案二)}\mid 方案一通过旋转得到方案二\}\)。

自反性：\((\text{方案一, 方案一})\in R\)。

对称性：\((\text{方案一, 方案二})\in R\Leftrightarrow (\text{方案二, 方案一})\in R\)。

传递性：\((\text{方案一, 方案二})\in R \land \text{方案二, 方案三})\in R\Rightarrow (\text{方案一, 方案三})\in R\)。

所以 \(R\) 是 \(\{所有方案\}\) 上的一个等价关系，将问题转化为求 的 \(\{所有方案\}\) 的 \(R\) 等价类有多少。

一般来说，我们可以把等价关系描述为：两个对象等价当且仅当一个对象可以通过 "某些操作" 变为另一对象，这促使我们考虑所有 "操作" 的集合的性质。

置换群

我们用置换群来刻画 "操作" 的集合。

置换

设 \(n\) 元集合 \(A = \{a_1, a_2\dots,a_n\}\)，将 \(A\) 上的一个一一映射 \(g:A\rightarrow A\) 称为 \(A\) 上的一个置换。

置换 \(g = [p_1, p_2,\dots, p_n]\) 表示 \(\forall i.g(a_i) = a_{p_i}\)。

• \(n\) 元集合上的置换有 \(n!\) 个。
• 将置换 \(g\) 的每个 \(i\) 指向 \(p_i\)，得到一个环的森林。

置换的复合

\(A\) 的置换 \(g, h\) 的复合是一个新的置换，记为 \(g\circ h\)，满足 \((g\circ h)(a_i) = g(h(a_i))\)。

例：假设 \(A = \{1,2, \dots, n\}, \ g = [2, 3, \dots, n, 1], \ h = [2, 3, \dots, n, 1]\)，则 \(g\circ h = [3,4,\dots,1,2]\)。

群

设集合 \(G\) 和一个定义在 \(G\) 上的二元运算 \(\circ:G\times G\rightarrow G\)，满足：

• 结合律：\(\forall a, b, c\in G.(a\circ b)\circ c = a\circ (b\circ c)\)。
• 单位元：\(\exists e\in G.\forall a\in G.a\circ e = e\circ a = a\)。
• 逆元：\(\forall a \in G.\exists b \in G. a\circ b = b\circ a = e\)，记为 \(a^{-1}\)。

则称 \((G, \circ)\) 是一个群。

1. \((\mathbb R,+)\)。

   结合律：\(\forall a, b, c\in \mathbb R.(a + b)+ c = a+ (b + c)\)。

   单位元：\(e = 0.\forall a\in \mathbb R.a + 0 = 0 + a = a\)。

   逆元：\(\forall a \in \mathbb R.a^{-1} = -a. a + (-a) = (-a) + a = 0\)。

2. 令 \(S_n\) 为全部 \(n\) 元置换的集合，\(\circ\) 为置换的复合，则 \((S_n, \circ)\) 是一个群。（对称群）

   结合律：\(\forall f, g, h\in S_n.(f\circ g)\circ h = f\circ (g\circ h)\)。

   \[\begin{cases} ((f\circ g) \circ h)(a_i) = (f\circ g) (h(a_i)) = f(g(h(a_i)))\\ \\ (f\circ (g \circ h))(a_i) = f(g\circ h(a_i)) = f(g(h(a_i)))\\ \end{cases} \]

   单位元：\(e = [1,2, \dots, n], \ \forall f\in S_n.f\circ e = e\circ f = f\)。

   逆元：\(\forall f \in G\)，\(f^{-1}\) 是其反函数。

置换群

\(G\) 是置换的集合，\(\circ\) 为置换的复合，且 \((G, \circ)\) 是一个群，称 \((G, \circ)\) 是一个置换群。（对称群的子群）

例：

设 \(n\) 元环的 \(n\) 个节点分别为 \(a_1, a_2\cdots, a_n\)，旋转操作可以看成 \(A = \{a_1, a_2, \cdots, a_n\}\) 上的 \(n\) 个置换，其中 \(g_i = [i + 1, i + 2,\cdots,n, 1\cdots,i]\)。

设集合 \(G = \{g_0, g_1, \cdots, g_{n - 1}\}\)，则 \((G, \circ)\) 是一个置换群，称为正 \(n\) 边形旋转群。

若 \(g_i, g_j\in G\)，则 \(g_i\circ g_j = g_{i + j\bmod n} \in G\)，所以复合运算关于 \(G\) 是封闭的。

单位元：\(g_0\)。逆元：\(g_i^{-1} = g_{n - i\bmod n}\)。

---

群对集合的作用

一个操作会将一个对象改变为另一个对象，形式化的：

设 \((G, \circ)\) 是一个群，其单位元为 \(e\)，群 \(G\) 对集合 \(X\) 的作用是一个 \(G\times X\) 到 \(X\) 的映射 \(f\)。

我们把 \(f(g, x)\) 记做 \(g_f(x)\) 或（没有歧义的情况下记成）\(g(x)\)，满足：

• \(\forall x\in X, f(e, x) = x\)。

• \(\forall g, h\in G.f(g\circ h, x) = f(h, f(h, x))\)。

• \(X\) 上的 \(G\) 关系：\(R_G = \{(x, y\mid x, y\in X \land (\exists g\in G.y = g(x))\}\)，即 \(y\) 通过 \(G\) 的作用能变成 \(x\)。

  具体的讲，一种染色方案能通过正 \(n\) 边形旋转群上的作用变为另一种，则称这两种方案是等价的。

• \(R_G\) 是等价关系，它将 \(X\) 划分为若干个等价类，每个等价类称为 \(X\) 上的 \(G\text{-}\)轨道。

例：

设 \(n\) 元环的 \(n\) 个节点分别为 \(a_1, a_2\cdots, a_n\)，令 \(A = \{a_1, a_2, \cdots, a_n\}\)。设颜色集合 \(B = \{b_1, b_2\cdots, b_m\}\)，染色操作可以看成 \(A\) 到 \(B\) 的映射，令 \(X\) 是所有这些映射的集合，即 \(X = \{x\mid x: A\rightarrow B\}\)。

令 \(G = \{g_0, g_1,\dots, g_{n - 1}\}\) 是正 \(n\) 边形旋转群，定义 \(G\times X\) 到 \(X\) 的映射 \(f\)。

其中 \(\forall i \in [0, n), x \in X.y = f(g_i, x)\) 满足 \(\forall j \in [0, n), \ y(a_j) =x(g(a_j) )\)，可以证明 \(f\) 是 \(G\) 对 \(X\) 的一个作用，简记 \(y = f(g_i, x)\) 或 \(y = g_i(x)\)。

实际意义就是先把 \(a_i\) 通过置换变为新的节点 \(a_j\)，再看 \(a_j\) 在原来的 \(x\) 上会被染成什么颜色，把这个颜色安排给 \(a_i\)。

\(X\) 上的 \(G\) 关系为 \(R_G = \{(x, y\mid x, y\in X \land (\exists g\in G.y = g(x))\}\)，\(xR_Gy\) 当且仅当染色方案 \(x\) 能通过旋转得到 \(y\)。

不同的染色方案，即 \(X\) 上 \(G\text{-}\) 轨道的数量。

---

Burnside 引理

定理

设有限群 \((G, \circ)\) 作用在有限集 \(X\) 上，则 \(X\) 的 \(G\text{-}\) 轨道数量为

\[N = \dfrac{1}{|G|}\sum_{g \in G} \psi(g) \]

其中 \(\psi(g)\) 表示满足 \(g(x) = x\) 的 \(x\) 的数量。

简单应用

给一个六元环的节点染色，共 \(m\) 种颜色，通过旋转得到的算一种方案，求方案数。

令 \(X = \{\{a_1, a_2, \dots, a_6\}\rightarrow\{b_1, b_2,\dots,b_m\}\}\)，\(G\) 是正六边形旋转群，分别是：

• \(e = [1, 2, 3, 4, 5, 6], \ \psi(e) = m^6\)。
• \(g_1 = [2, 3, 4, 5, 6, 1], \ \psi(g_1) = m\)。
• \(g_2 = [3, 4, 5, 6, 1, 2], \ \psi(g_1) = m^2\)。
• \(g_3 = [4, 5, 6, 1, 2, 3], \ \psi(g_1) = m^3\)。
• \(g_4 = [5, 6, 1, 2, 3, 4], \ \psi(g_1) = m^2\)。
• \(g_5 = [6, 1, 2, 3, 4, 1], \ \psi(g_1) = m\)。

因此 \(N = \dfrac{1}{6}(m^6 + m^3 + 2m^2 + 2m)\)。

对于每一种置换 \(g_i\)，让 \(a_j\) 向 \(g_i(a_j)\) 连边：

\(e = [1, 2, 3, 4, 5, 6]\)

\(g_1 = [2, 3, 4, 5, 6, 1]\)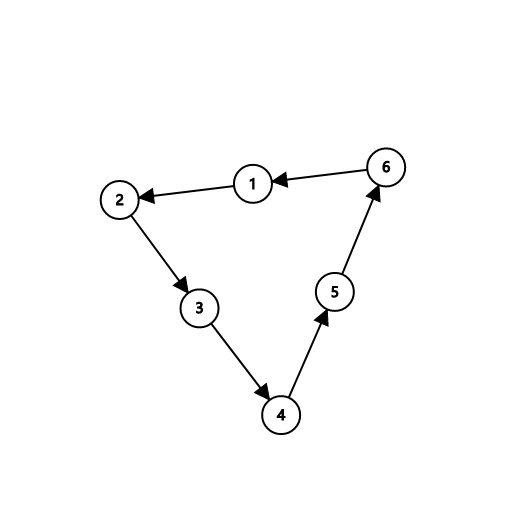

\(g_2 = [3, 4, 5, 6, 1, 2]\)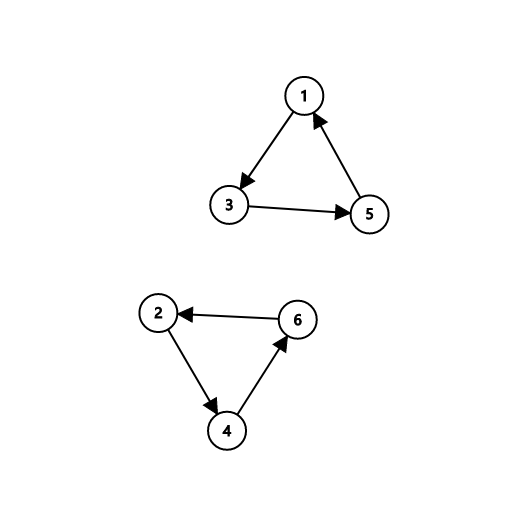

\(g_3 = [4, 5, 6, 1, 2, 3]\)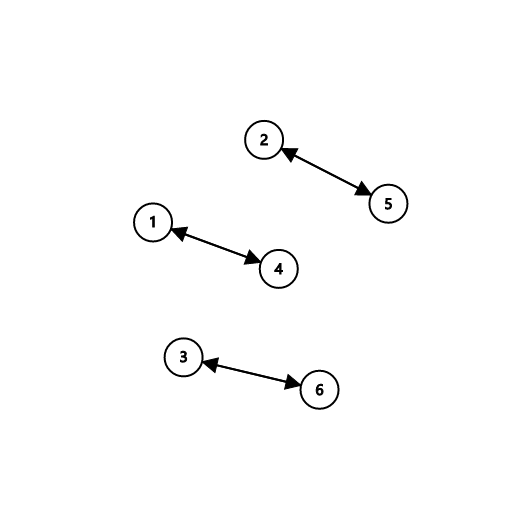

不难观察到，同一环内颜色只有相同才能保持不变，不同环间颜色任取。

于是每个 \(g_i\) 对应的不动点也非常好计算了。

推广到更一般的情况。

给一个 \(n\) 元环的节点染色，共 \(m\) 种颜色，通过旋转得到的算一种方案，求方案数。

• \(\psi(g_i) = m^{\gcd(n, i)}\)。

• \[\begin{aligned} N = &= \dfrac{1}{n}\sum_{i = 0}^{n - 1}m^{(n, i)}\\ \\ &= \dfrac{1}{n}\sum_{d \mid n}\sum_{i = 0}^{n - 1}[(n, i) = n/d]m^{n/d}\\ \\ &= \dfrac{1}{n}\sum_{d \mid n}\sum_{i = 0}^{n - 1}[(d, di/n) = 1]m^{n/d}\\ \\ &= \dfrac{1}{n}\sum_{d \mid n}\sum_{j = 0}^{d - 1}[(d, j) = 1]m^{n/d}\\ \\ &= \dfrac{1}{n}\sum_{d \mid n}\varphi(d)m^{n/d} \end{aligned} \]

---

置换群的轮换指标

置换群的轮换指标

• 轮换的形式：把置换群中的每个环上的节点按顺序记录下来，它是置换的另一种表现形式，比如 \(g = [3, 4, 5, 6, 1, 2] = (135)(246)\)。
• 置换形：如果 \(n\) 元置换 \(g\) 有 \(b_i\) 个长度为 \(i\) 的环，则称这个 \(g\) 形为 $ 1^{b_1}2\cdots n^{b_n}$。

设 \((G, \circ)\) 是一个 \(n\) 元置换群，则它的轮换指标为：

\[P_G(x_1, x_2,\dots,x_n) = \dfrac{1}{n}\sum_{g \in G} x_1^{b_1}x_2^{b_2}\cdots x_n^{b_n} \]

1. 正 \(n\) 边形旋转群的轮换指标：

\[P_G = \dfrac{1}{n}\sum_{d \mid n} \varphi(d)x_d^{n/d} \]

2. 正 \(n\) 边形二面体群（旋转，翻转为同一方案）的轮换指标：

   首先考虑群的大小，有 \(n\) 个旋转置换和 \(n\) 个翻转置换。

   如果 \(n\) 为偶数，

   那么它的一个翻转置换可能形为 \(1^22^{\frac{n - 2}{2}}\)（对角线作对称轴），可能形为 \(2^{n/2}\)（对边中点连线作对称轴），各 \(n / 2\) 个。

   如果 \(n\) 为奇数，则其所有翻转置换都形为 \(1^12^{\frac{n - 1}{2}}\)。

   所以正 \(n\) 边形二面体群的轮换指标为

   \[P_G = \dfrac{1}{2n}\sum_{d \mid n} \varphi(d)x_d^{n/d} + \begin{cases}\dfrac{1}{2}x_1x_2^{\frac{n - 1}{2}} & n\text{ 为奇数}\\ \\ \dfrac{1}{4}x_1^2x_2^{\frac{n - 2}{2}} + \dfrac{1}{4}x_2^{\frac{n}{2}}& n\text{ 为偶数}\end{cases} \]

有关正方体的置换群

顶点置换群

\[P_G = \dfrac{1}{24}(x_1^8 + 8x_1^2x_3^2 + 9x_2^4 + 6x_4^2) \]

边置换群

\[P_G = \dfrac{1}{24}(x_1^{12} + 8x_3^4 + 6x_1^2x_2^5 + 3x_2^6 + 6x_4^3) \]

面置换群

\[P_G = \dfrac{1}{24}(x_1^6 + 8x_3^2 + 6x_2^3 + 3x_1^2x_2^2 + 6x_1^2x_4) \]

证明：对置换分类，然后再看轮换个数。

• 不动：即恒等变换。
• 以两个相对面的中心连线为轴的 \(90^\circ\) 旋转：相对面有 3 种选择，旋转的方向有两种选择，共 6 个置换。
• 以两个相对面的中心连线为轴的 \(180^\circ\) 旋转：相对面有 3 种选择，旋转方向的选择对置换不再有影响，共 3 个置换。
• 以两条相对棱的中点连线为轴的 \(180^\circ\) 旋转：相对棱有 6 种选择，旋转方向对置换依然没有影响，共 6 个置换。
• 以两个相对顶点的连线为轴的 \(120^\circ\) 旋转：相对顶点有 4 种选择，旋转的方向有两种选择，共 8 个置换。

UVA10601 Cubes

题意：用 \(12\) 根木条搭建正方体，最多 \(6\) 种颜色，给出每根木条颜色，求能搭建不同的正方体的数量（不能在旋转翻转等操作后重合）。

\[P_G = \dfrac{1}{24}(x_1^{12} + 8x_3^4 + 6x_1^2x_2^5 + 3x_2^6 + 6x_4^3) \]

依次考虑公式的每一项，设第 \(i\) 种颜色有 \(c_i\) 个。

• \(x_1^{12}\) 表示染 \(12\) 个长度为 \(1\) 的环，不同的方案为 \(\dfrac{12!}{c_1!\cdots c_6!}\)。
• \(x_3^{4}\) 表示染 \(4\) 个长度为 \(3\) 的环，环内颜色相同，当且仅当 \(\forall c_i \bmod 3 = 0\) 时有 \(\dfrac{4！}{(c_1/3)!\cdots (c_6/3)!}\) 种不同的方案。
• 枚举两个一元环颜色，\(\sum\limits_{i ,j= 1}^6\dfrac{5!}{(c_1'/2)!\cdots (c_6'/2)!}\)。

后两项同样处理。

submission

Pólya 定理

• 集合 \(X\) 可以看成是给集合 \(A = \{a_1, a_2, \cdots, a_n\}\) 的每个元素赋予样式（颜色，种类等）的映射的集合。
• 引入表示式样的集合 \(B\)，令 \(X = \{f\mid f:A\rightarrow B\}\)，记为 \(B^A\)。
• \(G\) 在 \(B^A\) 上的作用：\(A\) 上的置换群 \(G\) 对 \(B^A\) 的作用为：\(g(f):a \to f(g(a))\)。
• 式样清单：\(G\) 作用在 \(B^A\) 上的 \(G\text{-}\) 轨道的集合称为 \(B^A\) 关于 \(G\) 的式样清单。

Pólya 定理（简化版）

\(B^A\) 关于 \(G\) 的式样清单记为 \(\mathcal{F}\)，则

\[|\mathcal{F}| = P_G(|B|, |B|, \dots, |B|) \]

Pólya 定理

• 种类的权值：假设 \(B\) 上的每个元素 \(b\) 都赋予了权值 \(w(b)\)。
• \(f \in B^A\) 的权值：定义 \(w(f) := \prod_{a \in A} w(f(a))\)。
• \(G\text{-}\) 轨道的权值（等价类）：\(w(F):=w(f)\)，任选一个 \(f \in F\)。

\[\sum_{F\in\mathcal{F}}w(F) = P_G(\sum_{b \in B}w(b), \sum_{b \in B}w(b)^2,\dots, \sum_{b \in B}w(b)^n) \]

具体应用

给 \(3\times 3\) 的方格染色，通过旋转或翻转可以得到的方案算同一方案，求有多少种方案满足恰好 \(2\) 个红格子，\(3\) 个蓝格子，\(4\) 个白格子。

先考虑群内置换数。

旋转置换：\(0^\circ, 90^\circ, 180^\circ, 270^\circ\)，共 \(4\) 个。

翻转置换：左右翻，上下翻，两条对角线，共 \(4\) 个。

有

\[P_G = \dfrac{1}{8}(x_1^9 + x_1x_2^4 + 2x_1x_4^2 + 4x_1^3x_2^3) \]

定义红色权值为 \(r\)，蓝色权值为 \(b\)，白色权值为 \(1\)。

将 \(x_i\) 替换为 \(r^i + b^i + 1\)。

\[f(r, b) = \dfrac{1}{8}[(r + b + 1)^9 + (r + b + 1)(r^2 + b^2 + 1)^4 + 2(r + b + 1)(r^4 + b^4 + 1)^2 + 4(r^3 + b^3 + 1)^3(r^2 + b^2 + 1)^3] \]

要求的东西恰为 \([r^2b^3]\) 的系数。（用多项式做不现实，常用 dp）

例题

E-远山的占卜

题意：\(2n\) 个元素排成一圈，\(k\) 种颜色，两种染色等价表示可以通过旋转或 翻转对角元素 得到，问本质不同的染色数。

由于对角是等效的，不妨把对角元素绑定，相当于一个 pair，那么元素对的颜色共 \(\dfrac{k(k + 1)}{2}\) 种。

\(n\) 个元素对的排列可以唯一对应一种 \(2n\) 个元素的排列。

则问题转化为 \(n\) 个点，\(\dfrac{k(k + 1)}{2}\) 种颜色的基本染色问题。

submission

POJ2888 Magic Bracelet

题意：长度为 \(n\) 的环形项链，\(m\)种颜色，每个珍珠可以任选一种颜色染色，但是规定了\(k\)对禁止关系\((a,b)\)，即不能存在颜色分别为 \(a,b\) 的珍珠相邻。

求本质不同的方案数。(通过旋转得到的项链为本质相同)

\[P_G = \dfrac{1}{n}\sum_{d \mid n} \varphi(d)x_d^{n/d} \]

回归到求 \(n / d\) 个长度为 \(d\) 的环的合法染色。

对于一个位置 \(p\)，\(p + d\) 与它在同一循环内，颜色相同。

因此，只要考虑 \([0, n/d)\) 的合法染色即可，注意 \(0\) 与 \(n/d - 1\) 也视作相邻。

构造颜色的邻接矩阵 \(G\)，\(G_{i, j} = [i, j\text{ 可以相邻}]\)。

一个染色方案唯一对应于一条经过 \(n / d\) 条边的路径。

很明显用矩阵快速幂做。

由于 \(c_0 = c_{n / d}\)（\(c\) 为颜色），最终方案为 \(\sum G^{n / d}_{i, i}\)，表示从颜色 \(i\) 经过 \(n / d\) 条边走回颜色 \(i\) 的不同路径数。

submisson

UVA11255 Necklace

题意：有\(n\)个珠子，其中\(a\)个白色，\(b\)个灰色，\(c\)个黑色，\((n=a+b+c)\)。用这 \(n\) 个珠子组成项链，能组成多少种不同的项链？若两条项链，其中一条通过旋转和翻转能变成另一条，则这两条项链视为相同。

\[P_G = \dfrac{1}{2n}\sum_{d \mid n} \varphi(d)x_d^{n/d} + \begin{cases}\dfrac{1}{2}x_1x_2^{\frac{n - 1}{2}} & n\text{ 为奇数}\\ \\ \dfrac{1}{4}x_1^2x_2^{\frac{n - 2}{2}} + \dfrac{1}{4}x_2^{\frac{n}{2}}& n\text{ 为偶数}\end{cases} \]

求 \(tot\) 个环，第 \(k\) 个环的长度为 \(sz_k\) 的合法方案，满足任意环内颜色相同。

定义 \(f_{k, i, j}\) 表示前 \(k\) 个环，用 \(i\) 个白，\(j\) 个灰的方案数。

讨论第 \(k\) 个环的颜色，稍微注意点边界。

\[f_{k, i, j} = f_{k - 1, i, j} + f_{k - 1, i - sz_k, j} + f_{k - 1, i, j - sz_k} \]

submission