学习笔记：FFT与拉格朗日插值

多项式的表示形式

系数表示与点值表示

假设 \(f(x)\) 是一个 \(n\) 次多项式，则 \(f(x)\) 的系数表示为 \(f(x) = a_nx^n + a_{n - 1}x^{n - 1} + \cdots + a_0\)

\(f(x)\) 的点值表示为 \((x_0, f(x_0)), \ (x_1, f(x_1)), \dots, (x_n, f(x_n))\)，其中 \(\forall i \neq j, \ x_i \neq x_j\)。

• \(n + 1\) 个点值可以表示一个 \(n\) 次多项式。

• 在点值表示下 \(n\) 次多项式的乘法复杂的为 \(O(n)\)。

  设 \(h(x) = f(x) \cdot g(x)\)，则 \(\forall i \in [0, n], \ h(x_i) = f(x_i) \cdot g(x_i)\)。

复数与单位根

复数的指数形式

\(a + bi = re^{i\theta}\)，其中 \(r = \sqrt {a^2 + b^2}, \ \tan \theta = \dfrac{b}{a}\)。

欧拉公式：\(e^{ix} = \cos x + i\sin x\)。

单位根

\(x^n = 1\) 在复数域上的根称为 \(n\) 次单位根。\(n\) 次单位根有 \(n\) 个，形式为 \(\omega_{n}^k = e^{i\frac{2k\pi}{n}}\)。

单位根在复平面上等分单位圆。

单位根的性质：

• \(\omega_n^k = \omega_{2n}^{2k}\)。
• \(\omega_{2n}^{k + n} = -\omega_{2n}^{k}\)

快速傅里叶变换(Fast Fourier Transform)

离散傅里叶变换(Discrete Fourier Transform)

将多项式 \(A(x) = a_0 + a_1x + \dots + a_{n - 1}x^{n - 1}\) 转化为其点值形式 \((\omega_n^k, \ A(\omega_n^k)), \ (k = 0, 1, \dots, n - 1)\)。

不妨令 \(n\) 为 \(2\) 的整次幂。

把原式拆成奇偶两部分，即 \(A(x) = (a_0 + a_2x^2 + \cdots + a_{n - 2}x^{n - 2}) + (a_1 + a_3x^3 + \cdots + a_{n - 1}x^{n - 1})\)。

令 \(B(x) = a_0 + a_2x + \cdots + a_{n - 2}x^{n / 2 - 1}, \ \ C(x) = a_1 + a_3x + \cdots + a_{n - 2}x^{n / 2 - 1}\)。

则 \(A(x) = B(x^2) + xC(x^2)\)。

对于 \(k \in [0, n / 2 - 1]\)

\[\begin{aligned} A(\omega_n^k) &= B(\omega_n^{2k}) + \omega_n^{k}C(\omega_n^{2k})\\ \\ &= B(\omega_{n / 2}^{k}) + \omega_n^{k}C(\omega_{n / 2}^{k})\\ \end{aligned} \]

对于另一半的点值，可用 \(A(\omega_n^{k + n / 2})\) 表示，即

\[\begin{aligned} A(\omega_n^{k + n / 2}) &= B(\omega_n^{2k + n}) + \omega_n^{k + n / 2}C(\omega_n^{2k + n})\\ \\ &= B(\omega_{n / 2}^{k}) - \omega_n^{k}C(\omega_{n / 2}^{k})\\ \end{aligned} \]

具体的讲，当 \(n = 8\) 时，各项存在如下关系：

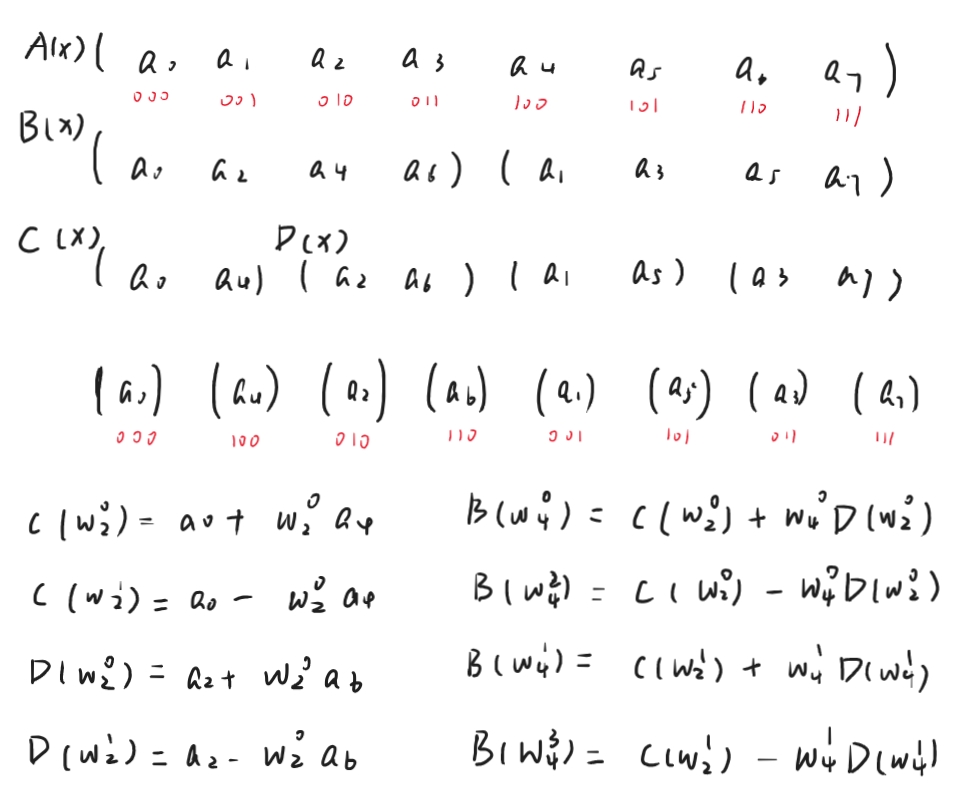
\(T(n) = 2T(n / 2) + O(n)\)。

可以直观看出，以这种方式将系数表示转化为点表示的时间复杂度为 \(O(n \log n)\)。

对于具体实现

• 分治（递归，常数大）。

• 蝴蝶变换（bit-reversal permutation）(非递归，常数小)。

  观察上图第一行和最后一行各项的二进制表示，互相颠倒。

  因此可以预处理最后一行的系数，自下而上递推。

逆离散傅里叶变换(Inverse DFT)

将多项式的点值表示 \((\omega_n^k, \ b_k), \ (k = 0, 1, \dots, n - 1)\) 转化为其系数表示 \(A(x) = a_0 + a_1x + \dots + a_{n - 1}x^{n - 1}\)。

设 \(n \times n\) 的矩阵 \(\Omega\)，其中 \(\Omega_{i, j} = \omega_n^{ij}\)，设向量 \(a = (a_0, a_1, \dots, a_{n - 1}), \ b = (b_0, _1, \dots, b_{n - 1})\)。

则 IDFT 相当于求解方程 \(\Omega a = b\)。

\[\begin{pmatrix} (\omega_n^0)^0 & (\omega_n^0)^1 & \cdots & (\omega_n^0)^{n - 1}\\ (\omega_n^1)^0 & (\omega_n^1)^1 & \cdots & (\omega_n^1)^{n - 1}\\ \vdots & \vdots& \ddots & \vdots \\ (\omega_n^{n- 1})^0 & (\omega_n^{n - 1})^1 & \cdots & (\omega_n^{n - 1})^{n - 1}\\ \end{pmatrix} \begin{pmatrix} a_0\\ a_1\\ \vdots\\ a_{n - 1} \end{pmatrix} = \begin{pmatrix} b_0\\ b_1\\ \vdots\\ b_{n - 1} \end{pmatrix} \]

如果我们能够求出 \(\Omega\) 的逆，则 \(a = \Omega^{-1}b\)。

设

\[M = \overline\Omega\cdot\Omega = \begin{pmatrix} (\omega_n^{-0})^0 & (\omega_n^{-0})^1 & \cdots & (\omega_n^{-0})^{n - 1}\\ (\omega_n^{-1})^0 & (\omega_n^{-1})^1 & \cdots & (\omega_n^{-1})^{n - 1}\\ \vdots & \vdots& \ddots & \vdots \\ (\omega_n^{-(n- 1)})^0 & (\omega_n^{-(n - 1)})^1 & \cdots & (\omega_n^{-(n- 1)})^{n - 1}\\ \end{pmatrix} \begin{pmatrix} (\omega_n^0)^0 & (\omega_n^0)^1 & \cdots & (\omega_n^0)^{n - 1}\\ (\omega_n^1)^0 & (\omega_n^1)^1 & \cdots & (\omega_n^1)^{n - 1}\\ \vdots & \vdots& \ddots & \vdots \\ (\omega_n^{n- 1})^0 & (\omega_n^{n - 1})^1 & \cdots & (\omega_n^{n - 1})^{n - 1}\\ \end{pmatrix} \]

其中

\[\begin{aligned} M_{i, j} &= (\omega_{n}^{-i})^{0}\cdot (\omega_{n}^{0})^{j} + (\omega_{n}^{-i})^{1}\cdot (\omega_{n}^{1})^{j} + \cdots(\omega_{n}^{-i})^{n - 1}\cdot (\omega_{n}^{n - 1})^{j}\\ \\ &= (\omega_{n}^{j-i})^{0} + (\omega_{n}^{j-i})^{1} + \cdots(\omega_{n}^{j-i})^{n - 1} \end{aligned} \]

相当于等比数列求和

\[M_{i, j} \begin{cases} \dfrac{1 - (w_n^{j - i})^n}{1 - w_n^{j - i}} = 0 \quad & w_n^{j - i} \neq 1\text{ 即 } i \neq j \\ \\ n \quad & i = j \end{cases} \]

令 \(\overline\Omega\) 满足 \(\overline\Omega_{i, j} = \omega^{-ij}\)，有 \(\overline\Omega\cdot\Omega = nI\)，因此

\[a = \dfrac{1}{n}\overline\Omega b \]

相当于给定 \(B(x) = b_0 + b_1x + \cdots + b_{n - 1}x^{n - 1}\)，求点值 \(a_k = B(\omega_n^{-k}), \ (0 \le k < n)\)。

例题

A * B Problem Plus

题意：给定 \(a, \ b\)，求 \(a \times b\)，\(a, \ b < 10^{50001}\)（范围可以更大）。

将 \(a\) 看作 \(a_0 + a_110^1 + a_210^2 + \cdots\)，fft 后再处理进位。

submission

SP8372 TSUM

题意：给定长度为 \(N\) 的数列 \(s\)，对于任意可能存在的 \(V\)，求满足 \(s_i + s_j + s_k = V, \ \ i < j < k\) 的对数，\(|s_i| \le 20000, \ N \le 40000\)。

构造多项式 \(A(x) = \sum x^{s_i}\)。

那么 \(\sum\limits_{i}\sum\limits_{j}\sum\limits_{k}[s_i + s_j + s_k = V] = [x^V]A^3(x)\)。

这样求得的数对不一定满足偏序关系，也不一定互不相同。

偏序关系很好处理，最后将答案除上 \(3!\) 即可。

现要除去存在位置相同的数对，考虑容斥。

性质 \(a_1: i = j\)，性质 \(a_2: i = k\)，性质 \(a_3:j = k\)。

1. 减去满足三个性质中一个的方案。

   钦定两个位置相等。

   令 \(B(x) = \sum x^{2s_i}\)，产生的方案为 \([x^V](A(x)B(x))\)。

2. 加上满足三个性质中两个的方案。

   \(i = j = k\)。

   令 \(C(x) = \sum x^{3s_i}\)，这部分的方案为 \([x^V]C(x)\)。

3. 减去满足三个性质中三个的方案。

   与第二部分相同。

则最终答案 \(D(x) = A^3(x) - 3B(x) + 2C(x)\)。

可以先对 \(A(x), \ B(x), \ C(x)\) 分别做 dft，计算出 \(D(x)\) 的点值，最后再对 \(D(x)\) 做 idft。

submission

FFT 在字符串匹配中的应用

普通的单模式串匹配

问题概述：给定模式串 \(a\)（长度为 \(m\)）、文本串 \(b\)（长度为 \(n\)），求所有位置 \(x\)，满足 \(B\) 串以 \(x\) 结尾的连续 \(m\) 个字符与 \(a\) 串完全相同。

定义匹配函数 \(C(x, y) = [a_x - b_y]^2\)，当 \(C(x, y) = 0\) 时则称 \(a\) 的第 \(x\) 个字符与 \(B\) 的第 \(y\) 个字符匹配。

定义完全匹配函数 \(P(x) = \sum\limits_{i = 0}^{m - 1}[a_i - b_{(x -m + i + 1)}]^2\)。

当且仅当 \(P(x) = 0\) 时以 \(x\) 结尾的连续 \(m\) 个字符与 $$ 匹a配。

令 \(s\) 串满足 \(s_i = a_{(m - i - 1)}\)，即 \(a\) 串的翻转。

于是 \(P(x) = \sum\limits_{i = 0}^{m - 1}[s_{(m - i + 1)} - b_{(x -m + i + 1)}]^2\)。

暴力展开：\(P(x) = \sum\limits_{i = 0}^{m - 1} s_{(m - i + 1)}^2 + \sum\limits_{i = 0}^{m - 1}b_{(x -m + i + 1)}^2 - \sum\limits_{i = 0}^{m - 1}2\cdot s_{(m - i + 1)}b_{(x - m + i + 1)}\)。

第一项为常数。

第二项可以预处理 \(f(x) = \sum_{i = 0}^xb_i^2\)，计算 \(f(x) - f(x - m)\)。

第三项等效于求 \(g(x) = \sum\limits_{i + j = x}s_ib_j\)。

则 \(P(x) = T + f(x) - f(x - m) - 2g(x)\)。

把字符串当作多项式，即 \(B(x) = b_0 + b_1x + b_2x^2 + \cdots\)。

则 \(g\) 为 \(S\) 与 \(B\) 的卷积。

最后检验多项式 \(P\) 有多少系数为 \(0\) 的项。

带通配符的单模式串匹配

问题概述：给定模式串 \(a\)（长度为 \(m\)），文本串 \(b\)（长度为 \(n\)），串的某些字符是 “通配符”（可以与任意字符匹配）。求所有位置 \(x\)，满足 \(b\) 串以 \(x\) 结尾的连续 \(m\) 个字符与 \(a\) 串完全相同。

总结思路：

1. 定义匹配函数。
2. 定义完全匹配函数。
3. 快速计算每一位的完全匹配函数（翻转模式串化为卷积）。

设通配符的数值为 \(0\)。

定义匹配函数 \(C(x, y) = [a_x - b_y]^2a_xb_y\)。

则完全匹配函数 \(P(x) = \sum\limits_{i = 0}^{m - 1}[a_i - b_{(x -m + i + 1)}]^2a_ib_{(x - m + i + 1)}\)。

将 \(a\) 翻转，\(P(x) = \sum\limits_{i = 0}^{m - 1}[s_{(m - i + 1)} - b_{(x -m + i + 1)}]^2\cdot s_ib_{(x - m + i + 1)}\)。

暴力展开：

\[\begin{aligned} P(x) &= \sum\limits_{i = 0}^{m - 1}[s_{(m - i + 1)} - b_{(x -m + i + 1)}]^2\cdot s_{(m - i + 1)}b_{(x -m + i + 1)}\\ \\ &= \sum\limits_{i = 0}^{m - 1} s_{(m - i + 1)}^3b_{(x - m + i + 1)} + \sum\limits_{i = 0}^{m - 1}s_{(m - i + 1)}b_{(x - m + i + 1)}^3 - \sum\limits_{i = 0}^{m - 1}2\cdot s_{(m - i + 1)}^2b_{(x - m + i + 1)}^2\\ \\ &= \sum_{i + j = x}s_i^3b_j + \sum_{i + j = x}s_ib_j^3 -2 \cdot \sum_{i + j = x}s_i^2b_j^2\\ \end{aligned} \]

把右边写成多项式乘积的形式，则

\[\begin{aligned} \\ P(x) = \sum s_i^3x^i \cdot \sum b_ix^i +\sum s_ix^i \cdot \sum b_i^3x^i -2\cdot \sum s_i^2x^i\cdot \sum b_i^2x^i\\ \\ \end{aligned} \]

例题

P4173 残缺的字符串

模板题。

#include<bits/stdc++.h>
using namespace std;
using namespace numbers;

using ll = long long;
constexpr int N = 6e5 + 5, tot = 1 << 19;

struct Complex {
	double x, y;
	Complex operator + (const Complex &o) const {
		return {x + o.x, y + o.y};
	}
	Complex operator - (const Complex &o) const {
		return {x - o.x, y - o.y};
	}
	Complex operator * (const Complex &o) const {
		return {x * o.x - y * o.y, x * o.y + y * o.x};
	}
} a[N], b[N], c[N];

int rev[N];

void fft(Complex a[], int Inv) {
	for(int i = 0; i < tot; ++ i) {
		if(i < rev[i]) {
			swap(a[i], a[rev[i]]);
		}
	}
	for(int mid = 1; mid < tot; mid <<= 1) {
		auto w1 = Complex({cos(pi / mid), Inv * sin(pi / mid)});
		for(int i = 0; i < tot; i += mid * 2) {
			auto wk = Complex({1, 0});
			for(int j = 0; j < mid; ++ j, wk = wk * w1) {
				auto x = a[i + j], y = a[i + j + mid];
				a[i + j] = x + wk * y;
				a[i + j + mid] = x - wk * y;
			}
		}
	}
	if(Inv == -1) {
		for(int i = 0; i < tot; ++ i) {
			a[i].x /= tot;
		}
	}
}

string s, t;
int m, n, A[N], B[N];

int main() {
	cin.tie(0)->sync_with_stdio(0);
	
	cin >> m >> n >> s >> t;
	reverse(s.begin(), s.end());
	for(int i = 0; i < m; ++ i) {
		A[i] = s[i] == '*' ? 0 : s[i] - 'a' + 1;
	}
	for(int i = 0; i < n; ++ i) {
		B[i] = t[i] == '*' ? 0 : t[i] - 'a' + 1;
	}
	
	for(int i = 0; i < tot; ++ i) {
		rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << 18);
	}
	
	for(int i = 0; i < tot; ++ i) {
		a[i] = Complex({A[i] * A[i] * A[i], 0});
		b[i] = Complex({B[i], 0});
	}
	fft(a, 1), fft(b, 1);
	for(int i = 0; i < tot; ++ i) {
		c[i] = c[i] + a[i] * b[i];
	}
	
	for(int i = 0; i < tot; ++ i) {
		a[i] = Complex({A[i], 0});
		b[i] = Complex({B[i] * B[i] * B[i], 0});
	}
	fft(a, 1), fft(b, 1);
	for(int i = 0; i < tot; ++ i) {
		c[i] = c[i] + a[i] * b[i];
	}
	
	for(int i = 0; i < tot; ++ i) {
		a[i] = Complex({A[i] * A[i], 0});
		b[i] = Complex({B[i] * B[i], 0});
	}
	fft(a, 1), fft(b, 1);
	for(int i = 0; i < tot; ++ i) {
		c[i] = c[i] - Complex({2, 0}) * a[i] * b[i];
	}
	
	fft(c, -1);
	
	vector<int> ans;
	for(int i = m - 1; i < n; ++ i) {
		ll v = c[i].x + 0.5;
		if(v == 0) {
			ans.push_back(i - m + 2);
		}
	}
	
	cout << ans.size() << '\n';
	for(int x : ans) cout << x << ' ';
	return 0;
}

CF528D

题意：给定只含 ATGC 的两个字符串 \(s, \ t\) 和一个非负整数 \(k\)，求有多少 \(i\) 满足任意 \(j \in [0, |t|)\)，都存在 \(p \in [0, |s|)\) 使得 \(|i + j - p|\le k\) 且 \(s_p = t_j\)。

记 \(s\) 的长度为 \(n\)，\(t\) 的长度为 \(m\)。

预处理第 \(i\) 个位置能否与字符 \(c\) 匹配，记做 \(b_{i, c}\)。

定义完全匹配函数 \(P(x)\)，表示以 \(x\) 结尾的字符串与 \(t\) 匹配的个数，匹配成功当且仅当 \(P(x) = m\)。

\(P(x) = \sum\limits_{c\in t}\sum\limits_{t_i = c}b_{(x - m + i + 1, c)}\)。

单独考虑每个字符，记 \(f(x, A) = \sum_{i = 0}^{m - 1}[t_i = A][b_{x - m + i + 1, A}]\)。

按照套路将 \(t\) 翻转。

则 \(f(x, A) = \sum_{i = 0}^{m - 1}[t'_{m -i - 1} = A][b_{x - m + i + 1, A}]\)。

令 \(T(x) = \sum_{i \ge 0} [t'_i = A]x^i, \ B(x) = \sum_{i \ge 0}[b_{i, A}]x^i\)，则 \(f(i, A) = [x^i]T(x)B(x)\)

submission

拉格朗日插值

拉格朗日插值定理

\(n\) 个点值 \((x_i, y_i), \ (1\le i \le n)\)，满足 \(x_i \neq x_j, \ (i\neq j)\)，它们 唯一 确定一个 \(n - 1\) 次多项式 \(f(x)\) 满足

\[f(x) = \sum_{i = 1}^ny_i\prod_{j \neq i}\dfrac{x - x_j}{x_i - x_j} \]

构造一个多项式 \(f(x) = f_1(x) + f_2(x) + \cdots + f_n(x)\)。

满足 \(f_i(x_j) = \begin{cases}y_j & i = j\\0 & i \neq j\end{cases}\)。

待定系数，\(f_1(x) = A(x - x_2)(x - x_3)\cdots(x - x_n)\)。

带入 \(x_1\)，解出 \(A = \dfrac{y_1}{(x_1 - x_2)(x_1 - x_3)\cdots(x_1 - x_n)}\)，其余 \(f_i\) 同理。

• 与 \(\text{CRT}\) 的关系？

  多项式模多项式：如果 \(f(x) = q(x)g(x) + r(x)\)，其中 \(r(x)\) 的次数小于 \(g(x)\)，则记做 \(f(x)\equiv r(x)\pmod {g(x)}\)。

  多项式互质：两个多项式的公因式只有常数，则称这两个多项式互质。

  对于任意 \(i \in [1, n]\)：

  \[f(x) - f(x_i) =a_1(x - x_i) + a_2(x - x_i^2) + \cdots a_{n - 1}(x^{n - 1} - x_i^{n - 1}) \equiv 0 \pmod{x - x_i} \]

  有同余方程组

  \[\begin{cases} f(x) \equiv f(x_1) \pmod {x - x_1}\\ \\ f(x) \equiv f(x_2) \pmod {x - x_2}\\ \\ \vdots\\ \\ f(x) \equiv f(x_{n - 1}) \pmod {x - x_{n - 1}}\\ \end{cases} \]

  显然有模数两两互质，满足中国剩余定理的使用条件。

• 暴力实现：先算 \(g(x) = \prod(x - x_i)\)，再求 \(n\) 次 \(g(x) / (x - x_i)\)，复杂度 \(O(n^2)\)。

• 特殊情况1：只要求一个 \(f(x_0)\)，复杂度 \(O(n^2)\)。

• 特殊情况2：只要求一个 \(f(x_0)\)，满足 \(x_i = i\)，复杂度 \(O(n)\)（可以预处理）。

例题

CF622F

题意：求 \(\sum_{i = 1}^ni^k\pmod {10^9 + 7}, \ n \le 10^9, \ k \le 10^6\)。

\(f(n) = \sum_{i = 1}^ni^k\) 是关于 \(n\) 的 \(k + 1\) 次多项式。

证明：

对于第二类斯特林数，满足公式

\[n^m = \sum\limits_{i = 0}^m\begin{Bmatrix}m\\i\end{Bmatrix}n^{\underline{i}} \]

那么

\[f(n) = \sum\limits_{i = 1}^n \sum\limits_{j = 0}^k\begin{Bmatrix}k\\j\end{Bmatrix}i^{\underline{j}} = \sum\limits_{j = 0}^k\begin{Bmatrix}k\\ j\end{Bmatrix}j!\cdot \sum\limits_{i = 1}^n\begin{pmatrix}i\\ j\end{pmatrix} \]

有组合恒等式

\[\sum\limits_{l = 0}^n\begin{pmatrix}l\\ k\end{pmatrix} =\begin{pmatrix}n + 1\\ k + 1\end{pmatrix} \]

则

\[f(n)= \sum\limits_{i = 0}^k\begin{Bmatrix}k\\ i\end{Bmatrix}i!\begin{pmatrix}n + 1\\ i + 1\end{pmatrix}= \sum\limits_{i = 0}^k\begin{Bmatrix}k\\ i\end{Bmatrix}\dfrac{(n + 1)^{\underline{i + 1}}}{i + 1} \]

所以求出 \([0, k + 1]\) 的函数值，直接拉插即可。

submission

Polynomia

题意：\(f(n)\) 是 \(n\) 次多项式，给定 \(f(i), \ i \in[0, n]\)，询问 \(s(R) - s(L - 1)\)。

\(f(n)\) 是 \(n\) 次多项式，则其前缀和为 \(n + 1\) 次多项式。

先对 \(f(n)\) 做一遍拉插求出 \(f(n + 1)\)，因而得到 \(s(n + 1)\)，再对 \(s\) 做拉插。

submission

reference

Ebola:浅谈FFT在字符串匹配中的应用