专题:数学
欧拉函数
定义
公式
对于所有质数,显然有 \(\phi(n) = n - 1\)。
对于 \(n = p_1^{a_1}p_2^{a_2}\cdots p_k^{a_k}\),
证明
- 如何求 \(p_i \mid x\) 的个数?\(\lfloor \dfrac{n}{p_i} \rfloor\)。
- 是否 \(\phi(n) = \sum \lfloor \dfrac{n}{p_i} \rfloor\)?重复计算了 \(p_1p_2 \mid x\) 的数量。
因此,我们对上式做一个容斥,得到
\(O(\sqrt n)\) 内求 \(\phi(n)\)
将质因数分解的过程与求 \(\phi\) 结合,直接套用公式。
结束循环时,\(n\) 一定是一个大于 \(\sqrt n\) 的质数,指数不可能超过 \(1\),因此直接乘 \(n - 1\)。
ll get_phi(ll n) {
ll phi = 1;
for(int i = 2; i <= n / i; ++ i) {
if(n % i == 0) {
phi *= (i - 1);
n /= i;
while(n % i == 0) n /= i, phi *= i;
}
}
if(n > 1) phi *= (n - 1);
return phi;
}
\(O(n)\) 求 \([1, n]\) 的欧拉函数
与欧拉筛相结合。
任意 \(n = p_1^{\alpha_1} \times p_2^{\alpha_2} \ldots \times p_k^{\alpha_k}\),只会被 \(i = p_1^{\alpha_1 - 1} \times p_2^{\alpha_2} \ldots \times p_k^{\alpha_k}\) 和 \(p_1\) 筛到。
- 若 \(p_1 > 1\),\(\phi(n) = \phi(i) \times p_1\)。
- 若 \(p_1 = 1\),\(\phi(n) = \phi(i) \times (p_1 - 1)\)。
int not_prime[N], prime[N], idx, phi[N];
void get_phi(int n) {
phi[1] = 1;
for(int i = 2; i <= n; ++ i) {
if(!not_prime[i]) prime[++ idx] = i, phi[i] = i - 1;
for(int j = 1; j <= idx && prime[j] * i <= n; ++ j) {
not_prime[prime[j] * i] = 1;
if(i % prime[j] == 0) {
phi[i * prime[j]] = phi[i] * prime[j];
break;
}
phi[i * prime[j]] = phi[i] * (prime[j] - 1);
}
}
}
欧拉定理
- 如果 \(\gcd(n, P) = 1\),那么 \(n^{\phi(P)} \equiv 1(\bmod P)\)。
费马小定理
当 \(P\) 本身即为质数时,得到欧拉定理的特殊形式,
求逆元
整数 \(n\) 在模 \(P\) 意义上存在逆元,当且仅当 \(\gcd(n, P) = 1\)。
proof:方程 \(nx = Py + 1\) 有解的充要条件为 \(\gcd(n, P) = 1\)。
\(O(\log n)\) 求 \(n^{-1}\)
在满足 \((n, P) = 1\) 的前提下,求解方程 \(nx = Py + 1\)。
\(x\) 即为 \(n^{-1}\)。
特别的,当 \(P\) 为质数时,\(n^{-1} = n^{P - 2}\),此时更常用的解法是快速幂。
\(O(n)\) 求 \([1, n]\) 的逆元
对于整数 \(i\),有 \(\lfloor \dfrac{P}{i} \rfloor \cdot i + P \% i = P\)。
所以
两边同乘 \(i^{-1} \cdot (P \% i)^{-1}\),得到
由于 \(P \% i < i\),可在 \(O(n)\) 时间内递推求得。
int inv[N];
void get_inv(int n, int P) {
inv[1] = 1;
for(int i = 2; i <= n; ++ i) {
inv[i] = -(P / i) * inv[P % i] % P;
}
}
例题
CF963A
题意:求 \(\sum \limits_{i=0}^{n} s_{i} a^{n - i} b^{i}\)。
把式子化成 \(a^n\sum \limits_{i=0}^{n} s_{i} a^{- i} b^{i}\)。
后面的部分可以进一步表示为首项为 \(\sum \limits_{i=0}^{k - 1} s_{i} a^{- i} b^{i}\),公比为 \(a^{-k}b^k\),项数为 \(\lfloor \dfrac{n + 1}{k} \rfloor\) 的等比数列。
最后处理余数。
submission
同余方程组的一般解
拓展中国剩余定理(EXCRT)
先考虑 \(k = 2\) 的情况。
设 \((y_{1_0}, y_{2_0})\) 是满足 \(y_1m_1 - y_2m_2 = a_2 - a_1\) 的一组解。
有 \(y_1 = y_{1_0} + k\dfrac{m_2}{(m_1, m_2)}\)。
所以
联立
推广到 \(k > 2\)
给出合并两组方程的实现,其中 mul 是龟速乘。
auto merge(ll a1, ll m1, ll a2, ll m2) {
ll y1, y2;
ll r = exgcd(m1, m2, y1, y2);
if((a2 - a1) % r != 0) {
cout << "NO";
exit(0);
}
ll m = m1 / r * m2;
y1 = mul(y1, (a2 - a1) / r, m);
ll a = (mul(y1, m1, m) + a1) % m;
return make_pair(a, m);
}
例题
POJ2891
POJ1006
CF338D
题意:给定 \(n\),\(m\) 和长度为 \(k\) 的序列,询问是否存在 \(1 \le x \le n\),\(1 \le y \le m - k + 1\),使得 \(\forall a[i] = \gcd(x, y + i - 1)\) 成立。
根据题意,一定有 \(\forall a_i \mid x,a_i \mid y + i - 1\),列出同余方程。
设 \(L = [a_1, a_2, \dots, a_k]\),显然有
对于 \(x = \lambda \cdot L\),必须满足 \(\gcd(\lambda, y) = 1\),否则 \(\gcd(x, y) > a_1\)。
\(x\) 钦定的情况下,我们要最小化 \(y\),否则会越界。
\(\lambda> 1\) 只会对 \(y\) 造成限制。
\(\rightarrow x = L\) 最优。
此时
所以只需检验 \(x = L\),\(y\) 等于满足 \(y \equiv y_0\) 的最小正整数解即可。
submission
同余方程组的构造解
中国剩余定理(CRT)
适用范围:模数两两互质。
设 \(M = [m_1, m_2, \cdots, m_k] = \prod m_i\)。
根据一般解的结论,\(x \equiv x_0 \pmod M\)。
待定系数:\(x \equiv \lambda_1a_1 + \lambda_2a_2 + \cdots + \lambda_ka_k \quad \pmod M\)。
满足第 \(i\) 个方程的充分条件是:
令 \(M_i = \dfrac{M}{m_i}\),\(M_i'M_i \equiv 1 \pmod {m_i}\)。
则
拓展欧拉定理
欧拉降幂公式
证明
例题
CF17D
题意:求 \((b - 1) b^{n - 1} \% c\),\(n, b \le 10^{10^6}\),\(c \le 10^9\)。
讨论 \(n - 1\) 与 \(\phi(c)\) 的关系,套用公式。
submission
CF906D
题意:给定数列 \(a_1,a_2,...,a_n\) 和模数 \(m\),每次询问一个区间 \([l,r]\),求 \(a_l^{a_{l+1}^{{...}^{a_r}}} mod m\) 的值。
考虑求 \(a_1^{a_2^{{...}^{a_k}}}\)。
递归地降幂。
第 \(1\) 层:讨论 \(a_1^{a_2^{{...}^{a_k}}}\) 与 \(\phi_1 = m\) 的关系,试图往 \(0\) 层降幂(实际没有)。
第 \(2\) 层:讨论 \(a_2^{a_3^{{...}^{a_k}}}\) 与 \(\phi_2 = \phi(\phi_1)\) 的关系,往第 \(1\) 层降幂。
第 \(3\) 层:讨论 \(a_3^{a_4^{{...}^{a_k}}}\) 与 \(\phi_3 = \phi(\phi_2)\) 的关系,往第 \(2\) 层降幂。
\(\vdots\)
第 \(k\) 层:讨论 \(a_k\) 与 \(\phi_k = \phi(\phi_{k - 1})\) 的关系,往第 \(k - 1\) 层降幂。
直接做是 \(O(nq\log V)\) 的,(每层回溯算结果要一只 log)。
如何优化?
当第 \(i\) 层的 \(\phi_i = 1\) 时,始终满足 \(a_i^{a_{i + 1}^{{...}^{a_k}}} \ge 1\),因此直接返回 \(1\)。
由于欧拉函数衰减很快,总复杂度 \(O(q\log^2V)\)。
submission
威尔逊定理
当 \(p\) 为质数时,有
证明
当 \(p = 2\) 时,\((2 - 1)! \equiv -1 \pmod 2\)
当 \(p > 2\) 时,即证 \(\prod\limits_{i = 2}^{p - 2} \equiv 1 \pmod p\)
方程 \(x^2 \equiv 1 \pmod p\) 成立当且仅当 \(x \equiv 1\) 或 \(x \equiv p - 1\)
所以 \(\forall x \in [2, p - 2]\),\(x^{-1} \in [2, p - 2]\) 且 \(x^{-1} \ne x\)
也就是 \(\dfrac{n - 3}{2}\) 对数两两匹配互为逆元。
推广
合数 \(n = p_1^{\alpha_1}\dots p_k^{\alpha_k}\)。
当 \(n\) 不为完全平方数时,\(p_1 \ne \dfrac{n}{p_1}\) 且 \(p_1, \ \dfrac{n}{p_1} < n\),所以 \(n \mid (n - 1)!\)。
当 \(n = p^2 时\):
如果 \(2p < n\),\(2p^2 \mid (n - 1)!\)
否则 \(n = 4\),\((4 - 1)! \equiv 2 \pmod 4\)
简单排列组合
隔板法
引入
求不定方程 \(x_1 + x_2 + \dots + x_k = n\) 的解的数量,满足 \(x_i \in N^*\),\(x_i \ge 1\)。
假想 \(n\) 个球,想要划分为不为空的 \(k\) 段。
这个问题等效于在 \(n - 1\) 个空隙中选出 \(k - 1\) 个并插入隔板。
所以解的数量为 \(C_{n - 1}^{k - 1}\)。
推广
1.求 $ x_1 + x_2 + \dots + x_k \le n$ 的解的数量,\(\forall x_i \ge a_i\)。
令 \(y_i = x_i - a_i + 1\),此时 \(y_i \ge 1\)。
将问题化归为 \(\sum \limits_{i = 1}^k y_i = n - \sum\limits_{i = 1}^k a_i + k\) 的解的数量,即可用上述结论求解。
特别的,当 \(\forall a_i = 0\) 时,方案数为 \(C_{n + k - 1}^{k - 1}\)。
2.求 $ x_1 + x_2 + \dots + x_k \le n$ 的解的数量。
增设 \(x_{k + 1} \ge 0\),满足 \(\sum \limits_{i = 1}^{k + 1} x_i = n\),用上述结论求解。
网格路径计数
问题引入:在 \(n \times m\) 的网格上,每次只能向右或向下,求 \((0, 0)\) 走到 \((n, m)\) 的路径数。
法1:\(O(nm)\) dp。
法2:组合意义。
把路径等效成长度为 \(n + m\) 的操作序列,只包括 '右' 和 '下' 两种元素。
一种方法是套用多重集不同排列的结论,方案为 \(\dfrac{(n + m)!}{n!m!}\)。
另一种方法是先假设操作序列空白,从中选 \(n\) 个填入 '下',其余填 '右',方案为 \(C_{n + m}^{m}\)。
例题
CF630C
题意:求有多少长度不大于 \(n\),只含 '7','8' 的数字, \(n \le 55\)。
数据很小,暴力求 \(\sum \limits_{i = 1}^{n} 2_i\) 没问题,也可以直接算 \(2^{n + 1} - 2\)。
CF629A
CF817B
CF131C
CF869C
题意:三种颜色岛屿各 \(a\),\(b\),\(c\) 座,相同颜色的岛屿的距离不小于 \(3\)(或不连通),求建桥的方案数。
- 一座岛不能和相同颜色的连边。
- 一座岛不能和两座颜色相同的岛连边。
所以对于岛 \(A_i\),最多向 \(B\) 连一条边,向 \(C\) 连一条边,且两边决策互不干扰。
枚举不同颜色的岛间连了几条边。
若 \((A, B)\) 连了 \(i\) 条边,则可选方案为 \(C_a^i \times C_b^i \times i!\)。
分开计算两两间的合法方案,最后相乘。
submisson
CF300C
题意:只含 \(a\),\(b\) 的数是好数,数位之和也是 '好数' 的 '好数' 是 '极好的数',求长度为 \(n\) 的 '极好的数' 个数。
数位之和取决于数字中 \(a\),\(b\) 的个数。
枚举有 \(i\) 个 \(a\)。
若 \(i \times a + (n - i) \times b\) 是 '好数',则在答案中加上 \(\dfrac{n!}{i!(n - i)!}\)。
submission
CF1312D
题意:求满足如下条件的长度为 \(n\) 的序列 \(a\) 的个数:
- \(\forall 1 \leq i \leq n\),都有 \(1 \leq a_i \leq m\)。
- \(a\) 中存在且仅存在一对相同的元素
- 存在一个位置 \(p\),使得 \(a_1 \sim a_p\) 为严格单增序列,\(a_p \sim a_n\) 为严格单减序列。
\(2 \leq n\le m \leq 2 \times 10^5\)。
钦定一对相同的元素 \(v\),剩下 \(n - 2\) 个数互不相同,共 \(C_{m - 1}^{n - 2}\) 种。
由于 \(a_p\) 一定大于 \(v\),减去所有数都小于 \(v\) 的 \(C_{v - 1}^{n - 2}\) 种情况。
至此,我们把整个序列划分为 【左 $\ \ \ v \ \ $ 左 $\ \ \ a_p \ \ $ 右 $\ \ \ v \ \ $ 右】。
还未分配的 \(n - 3\) 个元素要么在左,要么在右,与 \(2^{n - 3}\) 种合法方案一一对应。
所以答案为 \(2^{n - 3} \sum (C_{m - 1}^{n - 2} - C_{v - 1}^{n - 2})\)
CF991E
题意:给定正整数 \(n \le 10^{18}\),求满足条件的 \(m\) 的个数:
- \(m\) 没有前导零。
- \(m\) 中的数字 \(n\) 中都出现过。
- \(n\) 中的数字 \(m\) 中都出现过。
与 CF300C 相同,枚举每个数字的个数。
设 \(c_i\) 表示数字 \(i\) 出现的个数。
根据均值不等式,\(\prod \limits_{i = 0}^{9} c_i \le (\dfrac{\sum \limits_{i = 0}^{9} c_i}{10}) ^ {10} \le 613.11\),所以直接枚举的复杂的是正确的。
设 \(m = \sum \limits_{i = 0}^{9} c_i\),即当前数字位数。
讨论贡献:
- \(c_0 = 0 \rightarrow \dfrac{m!}{\prod \limits_{i = 0}^{9} c_i ! }\)
- \(c_0 \neq 0 \rightarrow \dfrac{m!}{\prod \limits_{i = 0}^{9} c_i ! } - \dfrac{(m - 1)!}{(c_0 - 1)!\prod \limits_{i = 1}^{9} c_i ! }\)
CF140E
题意:一棵 \(n\) 层的树,每层由 \(l_i\) 个小球组成。
-
同一层相邻的小球的颜色都不相同。
-
相邻的两层的小球颜色集合不相同。
一共有多少种合法装饰方案,对 \(p\) 取模。
钦定颜色列表 \([c_1, c_2, c_3, \dots, c_i, \cdots]\),令 \(f_{i, j}\) 表示一层内前 \(i\) 个位置恰好用前 \(j\) 种颜色的方案。
- 如果 \([1, i - 1]\) 用了 \(j - 1\) 种颜色,位置 \(i\) 只能放 \(c_j\)。
- 如果 \([1, i - 1]\) 用了 \(j\) 种颜色,位置 \(i\) 可以放 \(c_k\),\(c_k != a_{i - 1}\)。
因此
令 \(g_{i, j}\) 表示第 \(i\) 层,钦定颜色列表,且恰好用 \(j\) 种颜色的方案,
\(s_i\) 表示第 \(i\) 层的方案总数。
由于每层的颜色列表可以随意选择并排列:
\(g_{i, j}\) 不能从全部 \(s_{i - 1}\) 种前置状态转移过来,
如果 \(j \le l_{i - 1}\),则有 \(g_{i - 1, j} \times j!\) 个状态与当前钦定的颜色集合相同,所以
注意:
- 本题的 \(p\) 不是特殊的,采用 \(A_m^i = \prod \limits_{j = 1}^{i} (m - j + 1)\) 计算。
HDU7133
题意:长度为 \(n\) 的所有排列按字典序排序组成长度为 \(n!n\) 的新序列,有多少子串是 \(m\) 元排列?
完整排列的方案
把 \(\{1, 2, \dots, m - 1, m\}\) 看作整体,与剩余 \(n - m\) 个数进行排列。
算上内部顺序共 \(m!(n - m + 1)!\)。
跨块方案
Hint 1:已知排列 \(\{p_i\}\),怎么构造下一个排列?
- 找到最大的 \(k\) 使得 \(\{p_{k + 1}, \dots ,p_n\}\) 是最长下降后缀,即 \(p_k < p_{k + 1}\),\(\forall i \in [k + 1, n), p_i > p_{i + 1}\),
- 将 \(p_k\) 与后缀中第一个大于他的数字交换。
- 将 \(\{p_{k + 1}, \dots ,p_n\}\) 升序排序。
eg:13542 最长下降后缀为 542,前一位为 3,交换 3 和 4 得到 14532,重新排序得到 14235,即为下一个排列。
假设当前排列为 \(\{p_i\}\),下一个排列为 \(\{q_i\}\)。
性质 1:\(\{p_i\}\) 首尾元素 \(\le m\),大于 \(m\) 的都在中间。
| \(A\) | \(B\) | \(C\) |
|---|---|---|
| \(\le m\) | \(> m\) | \(\le m\) |
最终排列由 \(\{p_i\}\) 的 \(C\) 和 \(\{q_i\}\) 的 \(A\) 构成。
所以 \(\forall i \in C, p_i \le m\)。
把中间 \(n - m\) 个元素当成整体,插入剩下 \(m\) 个元素的 \(m - 1\) 个空隙中。
满足性质 1 的方案有 \(m!(n - m)!(m - 1)\)。
假设存在 \(i \in A, p_i > m\),则存在 \(i \in B, p_i \le m\)。
根据提示 1,最长后缀不存在于 \(A\),\(A\) 中元素不发生改变,\(\forall i \in A, p_i = q_i\)。
而 \(\forall i \in A, q_i \le m\),矛盾。
性质 2:\(\{p_i\}\) 的首部与 \(\{p_i\}\) 完全相同。
由性质 1 推出,\(A_p\) 与 \(C_p\) 关于 \(\{1, 2, \dots, m\}\) 互补。
又因为 \(C_p\) 与 \(A_q\) 互补,所以 \(A_p = A_q\)。
不满足性质 2 当且仅当首部发生改变,也就是 \(BC\) 段严格递减。
枚举尾部长度,不满足性质的方案共 \((n - m)!\sum \limits_{i = 1}^{m - 1} C_m^i (m - i)! = m!(n - m)!\sum \limits_{i = 1}^{m - 1} \dfrac{1}{i!}\)。
预处理 \(\dfrac{1}{i!}\) 前缀和,跨块总贡献为 \(m!(n - m)! (m - 1 - \sum \limits_{i = 1}^{m - 1} \dfrac{1}{i!})\)
容斥原理
引入
- 求 \(1\) 到 \(n\) 中既不是 \(2\) 的倍数也不是 \(3\) 的倍数的个数。
-
求 1 到 \(n\) 的全排列中 \(1\) 和 \(2\),\(3\) 和 \(4\) 都不相邻的方案。
将 \(1\),\(2\) 绑定,\(1\),\(2\) 相邻的方案数为 \(2!(n - 1)!\),同理 \(3\),\(4\)。
- \(n\) 件不同物品放入 \(3\) 个不同盒子,求方案数。
- 无限制条件 \(\rightarrow 3^n\)
- A(B,C)为空 \(\rightarrow 2^n\)
- AB(AC,BC)为空 \(\rightarrow 1\)
- ABC 为空 \(\rightarrow 0\)
一般形式
贡献法证明。
\(\forall x \in S - \bigcup\limits_{i = 1}^n A_i\),都在 \(i = 0\) 时产生 \(1\) 的贡献。
如果 \(x \in A_1, A_2, A_3, \dots, A_k\),则产生 \(\sum\limits_{i = 1}^{k} (-1)^i C_k^i\) 的贡献。
将 \((1 + 1)^k\) 与 \((1 - 1)^k\) 的二项式展开相加得到 \(C_k^i\) 的偶数项和,相减得到奇数项和。
可以证明 \(\sum\limits_{i = 1}^{k} (-1)^i C_k^i = 0\)。
- \(m\) 个物品分配给 \(n\) 个人,每个人至少一件,求分配方案数。
- \(2n\) 个元素 \(a_1, a_2, \dots, a_n\) 和 \(b_1, b_2, \dots, b_n\),求有多少个排列满足任意 \(a_i\) 不与 \(b_i\) 相邻。
- 欧拉函数证明。
不定方程的解的数量
求不定方程 \(x_1 + x_2 + \dots + x_k = n\) 的解的数量,满足 \(x_i \in N\),\(l_i \le x_i \le r_i\)。
只有下界的情况在隔板法中讲过。
利用容斥原理,把问题转化为 \(\forall i, x_i \ge l_i\) 的方案减去 \(\exists i, x_i \ge r_i + 1\) 的方案。
令 \([x]\) 表示一组解。
- \(S \leftarrow \{[x] \mid \forall i, \ x_i \ge l_i\}\)
- \(A_i \leftarrow \{[x] \mid a_i \ge r_i + 1, \quad \forall j \ne i, \ x_j \ge l_j\}\)
其中
等效于枚举 \(x_i\) 的下界是 \(l_i\) 还是 \(r_i + 1\),复杂度 \(O(2^k)\)。
错排问题
求 \(\forall i \in [1, n], a_i \le i\) 的排列数。
- \(S \leftarrow \{\{p\}\}\)
- \(A_i \leftarrow \{\{p\} \mid a_i = i\}\)
性质:\(n \rightarrow +\infty,\quad d(n) \rightarrow \dfrac{1}{e}\)。
容斥原理的符号形式
设 \(S\) 是一个有限集,\(a_1, a_2, \dots, a_n\) 是 \(n\) 种性质。
- 记 \(N(a_i)\) 为 \(S\) 中有 \(a_i\) 性质的元素的数量。特殊的,记 \(N(1) = |S|\)。
- 记 \(N(1 - a_i)\) 为 \(S\) 中没有 \(a_i\) 性质的元素的数量。
- \(N(a_{i_1}a_{i_2}\dots a_{i_k})\) 为 \(S\) 中同时有 \(a_{i_1}, a_{i_2},\dots, a_{i_k}\) 性质的元素的数量。
- \(N(a \pm b) = N(a) \pm N(b)\)。
- 当且仅当 \(a\) 与 \(b\) 独立时 \(N(ab) = N(a)N(b)\)。
则容斥原理可以写成
公式中枚举的 \(i\) 表示不满足的性质数。
符号形式在集合关系与多项式运算之间建立了桥梁。
- \((1 - A)(1 - B) = 1 - (A + B) + AB\)
- \(|S - A \cup B| = |S| - (|A| + |B|) + |A \cap B|\)
- \(N((1 - A)(1 - B)) = N(1 - (A + B) + AB) = |S| - (|A| + |B|) + |A \cap B|\)
容斥原理的推广
有了符号形式,我们可以方便在总方案中表示性质的有无,并通过多项式展开求解容斥关系。
因此可以解决有些性质有,有些性质没有的方案数。
如
- 求 \(1\) 到 \(n\) 中不是 \(2\) 也不是 \(3\) 的倍数,但是是 \(5\) 的倍数的数量。
- 求刚好有 \(k\) 个位置使得 \(p_i = i\) 的排列数。
由于 \(a_1\dots a_k\) 与 \((1 - a_{k + 1})\dots (1 - a_n)\) 独立,能够分开计算。
例题
NC15079
NC16513
NC19857
题意:\(n\) 对情侣围成一圈,求任意情侣不相邻的方案。
前置:长度为 \(n\) 的圆排列共 \((n - 1)!\)。
将选出的 \(i\) 对情侣绑定,将原集合等效成 \(2n - i\) 个元素进行排列。
本题卡空间,在线算组合又卡时间,容斥做法拿到 70pts 就够了,时空复杂度更优的做法。
submission
CF547C
题意:维护一个可重集,每次查询集合中互质数对的个数。
- 两个数互质取决于是否有共同的质因子。
- 小于 \(5\times 10^5\) 的数最多有 \(7\) 个不同质因子。
令 \(cnt_x\) 表示当前集合中能被 \(x\) 整除的数的个数。
考虑新增一个元素 \(cur = p_1^{\alpha_1}\dots p_k^{\alpha_k}\)。
令性质 \(a_i\) 表示能被 \(p_i\) 整除。
则
删除同理。
submission
[CQOI2012] 局部极小值
题意:在 \(n \times m\) 的矩阵中,\(1\) 到 \(n \times m\) 的每个整数恰好出现一次,\(n \le 4, m \le 7\)。
一个数是局部最小值当前仅当小于所有周围的数。
给定局部最小值的位置和非局部最小值的位置,求满足此要求的矩阵个数。
令性质 \(a_{i, j}\) 表示 \((i, j)\) 是局部最小值。
则要求的方案为 \(N(a_{i_1, j_1} \dots a_{i_k, j_k} (1 - a_{i_{k + 1},j_{k + 1}})\dots (1 - a_{i_{nm},j_{nm}}))\)。
于是转化为求解子问题 \(N(\prod a_{i, j})\)。
\(4 \times 7\) 的矩阵中最多有 \(8\) 个局部最小值,所以子问题规模小于 \(\sum\limits_{i = 0}^{8} C_{28}^i\),大约在 \(10^4\),可以接受。
通过搜索枚举子问题。
当钦定某些位置是局部最小时,如何求方案数?
不妨从小到大填充矩阵。
设 \(f_{i, s}\) 表示当前填到 \(i\),且局部最小的状态(填/没填)为 \(s\) 时的方案。
\(cnt_s\) 表示状态为 \(s\) 时填了多少个钦定位置。
如果当前填的位置钦定了局部最小,那么 \(f_{i, s} = \sum\limits_{j \in s} f_{i - 1, s - j}\)。
如果当前填的位置没有钦定,
用 \(nums_s\) 表示状态 \(s\) 下已经能填的非钦定位置个数。
如
此时只有 \((2, 3)\) 能填,否则会在后续产生矛盾。
则这部分的贡献为 \(\max(0, nums_s - (i - 1 - cnt_s)) \times f_{i - 1, s}\)。
\(i - 1 - cnt_s\) 为前 \(i - 1\) 个数中已经用掉的位置。
第二类斯特林数(Stirling Number)
第二类斯特林数(斯特林子集数)\(\begin{Bmatrix}n\\ k\end{Bmatrix}\),也可记做 \(S_2(n,k)\),表示将 \(n\) 个两两不同的元素,划分为 \(k\) 个互不区分的非空子集的方案数。
递推式
我们插入一个新元素时,有两种方案:
- 将新元素放入一个现有的非空子集,有 \(k\begin{Bmatrix}n-1\\ k\end{Bmatrix}\) 种方案。
- 将新元素单独放入一个子集,有 \(\begin{Bmatrix}n-1\\ k-1\end{Bmatrix}\) 种方案;
边界是 \(\begin{Bmatrix}n\\ 0\end{Bmatrix}=[n=0]\)。
通项公式
不妨先认为 \(k\) 个集合互不相同,转化成经典容斥问题,最后乘上 \(\dfrac{1}{k!}\)。
则
重要公式
我们记下降阶乘幂 \(x^{\underline{n}}=\dfrac{x!}{(x-n)!}=\prod_{k=0}^{n-1} (x-k)\)。
则可以利用下面的恒等式将普通幂转化为下降幂:
考虑各式组合意义。
- \(x^n \rightarrow\) \(n\) 个不同的球放入 \(x\) 个不同的盒子。
- \(\begin{pmatrix}x\\ k\end{pmatrix} \rightarrow\) \(x\) 个盒子中选出 \(k\) 个。
- \(\begin{Bmatrix}n\\ k\end{Bmatrix} \rightarrow\) \(n\) 个不同的球放入 \(k\) 个相同的盒子且都不为空。
- \(k! \rightarrow\) 将选出的 \(k\) 个盒子排列。
正确性显然。
积性函数
定义
若函数 \(f(n)\) 满足 \(f(1)=1\) 且 \(\forall x,y\in\mathbf{N}^*,~(x,y)=1\) 都有 \(f(xy)=f(x)f(y)\),则 \(f(n)\) 为 积性函数。
若函数 \(f(n)\) 满足 \(f(1)=1\) 且 \(\forall x,y\in\mathbf{N}^*\) 都有 \(f(xy)=f(x)f(y)\),则 \(f(n)\) 为 完全积性函数。
例如:
- 单位函数:\(\varepsilon(n)=[n=1]\)。(完全积性)
- 恒等函数:\(\operatorname{id}_k(n)=n^k\),\(\operatorname{id}_{1}(n)\) 通常简记作 \(\operatorname{id}(n)\)。(完全积性)
- 常数函数:\(1(n)=1\)。(完全积性)
- 除数函数:\(\sigma_{k}(n)=\sum_{d\mid n}d^{k}\)。\(\sigma_{0}(n)\) 通常简记作 \(d(n)\) 或 \(\tau(n)\),\(\sigma_{1}(n)\) 通常简记作 \(\sigma(n)\)。
- 欧拉函数:\(\varphi(n)=\sum_{i=1}^n[(i,n)=1]\)
- 莫比乌斯函数:\(\mu(n)=\begin{cases}1&n=1\\0&\exists d>1,d^{2}\mid n\\(-1)^{\omega(n)}&\text{otherwise}\end{cases}\),其中 \(\omega(n)\) 表示 \(n\) 的本质不同质因子个数,它是一个加性函数。
"加性函数"
此处加性函数指数论上的加性函数 (Additive function)。对于加性函数 \(f\),当整数 \(a,b\) 互质时,均有 \(f(ab)=f(a)+f(b)\)。
应与代数中的加性函数 (Additive map) 区分。
性质
若 \(f(x)\) 和 \(g(x)\) 均为积性函数,则以下函数也为积性函数:
设 \(x=\prod p_i^{k_i}\)
若 \(F(x)\) 为积性函数,则有 \(F(x)=\prod F(p_i^{k_i})\)。
若 \(F(x)\) 为完全积性函数,则有 \(F(x)=\prod F(p_i)^{k_i}\)。
质因数分解求 \(f(n)\)
\(f(n) = f(p_1^{\alpha_1})\dots f(p_k^{\alpha_k})\)。
对 \(f(p_1^{\alpha_1})\) 依次求解然后相乘即可。
ll get_f(int n) {
ll ret = 1;
for(int i = 2; i <= n / i; ++ i) {
if(n % i == 0) {
int cnt = 0;
while(n % i == 0) {
++ cnt;
n /= i;
}
ret = ret * calc_f(i, cnt);
}
}
if(n > 1) {
ret = ret * calc_f(n, 1);
}
return ret;
}
欧拉筛求 \(f(1), f(2), \dots, f(n)\)
根据定义:\(f(1) = 1\)。
\(n = p_1^{\alpha_1} \dots p_k^{\alpha_k}\) 一定会被 \(m = p_1^{\alpha_1 - 1} \dots p_k^{\alpha_k}\) 筛到。
- 如果 \(\alpha_1 = 1\),则 \((n, m) = 1\),\(f(n) = f(m) \cdot f(p_1)\)。
- 如果 \(\alpha_1 > 1\),则 \((n, m) \ne 1\),\(f(n) = \dfrac{f(m)}{f(p_1^{\alpha_1 - 1})} \cdot f(p_1^{\alpha_1})\)。
因此,对于质数的幂次 \(p^{cnt}\),暴力调用 calc_f(p, cnt)。
否则,记录数组 \(cnt_i\) 表示 \(i\) 中最小质因子的次数,根据上述分类求解。
void init(int n) {
f[1] = 1;
for(int i = 2; i <= n; ++ i) {
if(v[i] == 0) {
p[++ idx] = i;
cnt[i] = 1;
f[i] = calc_f(i, 1);
}
for(int j = 1; p[j] <= n / i; ++ j) {
v[i * p[j]] = 1;
if(i % p[j] == 0) {
cnt[i * p[j]] = cnt[p[j]] + 1;
f[i * p[j]] = f[i] / calc_f(p[j], cnt[p[j]]) * calc_f(p[j], cnt[p[j]] + 1);
break;
}
cnt[i * p[j]] = 1;
f[i * p[j]] = f[i] * calc_f(p[j], 1);
}
}
}
例题
NC229685
题意:求 \(n\) 的正因子个数,\(q\) 次询问,\(n \le 10^7\)。
若 \(n = p_1^{\alpha_1}\dots p_k^{\alpha_k}\),则 \(f(n) = (\alpha_1 + 1)\dots(\alpha_k + 1)\)。
若 \((p, q)\) 互质,则 \(f(p)\cdot f(q) = (\alpha_1 + 1)\dots(\alpha_k + 1)(\beta_1 + 1)\dots(\beta_l + 1) = f(p\cdot q)\)
NC23047
题意:求 \(\bigoplus\limits_{i = 1}^n (i^n \bmod (10^9 + 7))\),\(n \le 1.3 \times 10^7\)。
定义 \(f(i) = i^n\)。
对于 \(\forall p, q, \ \ f(pq) = (pq)^n = p^nq^n\),是完全积性的。
CF757E
题意:定义函数 \(f_r(n)\):
- \(f_0(n)\) 为满足 \(p\cdot q=n\) 且 \(\gcd(p,q)=1\) 的有序对 \((p,q)\) 个数;
- \(\displaystyle f_{r + 1}(n)=\sum_{u\cdot v=n}\frac{f_{r}(u)+f_{r}(v)}{2}\).
一共 \(q\) 组询问,每组询问给出 \(r,n\),求 \(f_r(n)\) 模 \(10^9+7\) 的结果。
数据范围:\(q\le10^6\),\(0\le r\le10^6\),\(1\le n\le10^6\).
对于 \(n = p_1^{\alpha_1}\dots p_k^{\alpha_k}\),只有 \(p = \prod\limits_{i \in S}p_i^{\alpha_i} , \ q = \prod\limits_{i \notin S}p_i^{\alpha_i}\) 时会对 \(f_0(n)\) 造成贡献。
所以 \(f_0(n) = 2^k = 2^{\sigma(n)}\).
对于 \((p, q) = 1\),\(\{p_i\} \cap\{q_i\} = \phi\).
所以 \(\sigma(pq) = \sigma(p) + \sigma(q)\).
所以 \(f_0(pq) = f_0(p)\cdot f_0(q)\),于是我们证明了 \(f_0\) 是积性函数。
现在考虑 \(r \ge 1\).
注意到 \((u, v)\) 与 \((v, u)\) 都有贡献,所以 \(\forall d \mid n\) 对 \(f_r(n)\) 的贡献为 \(2 \times \dfrac{f_{r - 1}(d)}{2}\)。
考虑积性函数 \(f(n)\),以及函数 \(g(n) = \sum\limits_{d\mid n}f(d)\).
对于 \((p, q) = 1\),有
所以 \(g(n)\) 也是积性函数。
因为 \(f_0\) 是积性函数,所以 \(\forall r, (p, q) = 1, \ f_r(p\times q) = f_r(p) \times f_r(q)\).
于是目标 \(f_r(n) = f_r(p_1^{\alpha_1})\times \dots \times f_r(p_k^{\alpha_k})\),只需预处理 \(\forall r, p, \alpha, \ \ f_r(p^{\alpha})\) 即可。
不妨从 \(f_0\) 开始递推。
- \(\alpha = 0\),\(f_0 = 1\).
- \(\alpha > 0\),\(f_0 = 2\).
\(f_0(p^{\alpha})\) 的值与 \(p\) 无关。
根据递推式 \(f_r(p^{\alpha}) = \sum\limits_{i = 0}^{\alpha} f_{r - 1}(p^i)\),\(f_r\) 只与 \(f_{r - 1}\) 有关,所以 \(\forall r\),\(f_r(p^{\alpha})\) 的值与 \(p\) 无关。
记 \(dp_{r, i} = f_r(p^i)\).
莫比乌斯反演
引入
- 如果 \(f(n) = \sum\limits_{i = 1}^ng(i)\),则 \(g(n)\) 可通过 \(f(n) - f(n - 1)\) 反求。
- 如果 \(f(n) = \sum\limits_{d \mid n} g(d)\),怎么通过 \(f\) 反求 \(g(n)\)?
如果 \(n = p_1^{\alpha_1}\dots p_k^{\alpha_k}\).
令性质 \(a_i\) 不整除 \(p_i^{\alpha_i}\),则 \(N(a_i) = f(p_1^{\alpha_1}\dots p_i^{\alpha_i - 1}\dots p_k^{\alpha_k})\).
则
引入莫比乌斯函数 \(\mu(n) = [n = p_1\dots p_i](-1)^i\).
即
于是
定理(莫比乌斯反演)
设 \(f:\mathbb{N} \rightarrow \mathbb{R}, \ g:\mathbb{N} \rightarrow \mathbb{R}\) 是两个函数,则
环计数问题
题意:\(n\) 个数围成一圈,每个数取值范围在 \(1\) 到 \(r\),求有多少个这样的环,两个环不相同当且仅当不能通过旋转重合。
将 \(n\) 个数展开成序列并无限延伸。
定义周期 \(d\) 为满足 \(\forall a_i = a_i + d\) 的最小正整数。
显然 \(d \mid n\),否则与 \(\forall a_i = a_i + n\) 矛盾。
令 \(f(d)\) 表示周期为 \(d\) 的不同环的个数。
一个环对应 \(d\) 个不同的序列(分别以 \(a_1, a_2\dots a_d\) 开头)。
所有不同的序列共 \(r^n\) 个。
所以
总方案数为 \(\sum\limits_{d = 1}^n f(d)\).
定理(莫比乌斯反演2)
设 \(f:\mathbb{N} \rightarrow \mathbb{R}, \ g:\mathbb{N} \rightarrow \mathbb{R}\) 是两个函数,且存在正整数 \(N\),使得 \(\forall n > N, \ f(n) = g(n) = 0\).
则
例题
NC14648
题意:给定序列 \(\{a_i\}, \ \{b_i\}\),有多少对 \((x, y) = 1\) 满足 \(a_{b_x} = b_{a_y}\).
定义 \(g(d) = \sum\limits_{x, y}[(x, y) = d][a_{b_x} = b_{a_y}]\),考虑反演:
则
其中 \(\forall f_i\) 可以在 \(O(\dfrac{n}{1} + \dfrac{n}{2} + \cdots + \dfrac{n}{n}) = O(n\ln n)\) 内求出。
AT_abc162_e
题意:给定\(n,k\),求
和上题套路一致,设 \(g(d) = \sum [\gcd(a_i) = d]\).
有反演:
若 \(d \mid \gcd(a_i)\),则 \(\forall i, \ d \mid a_i\),所以 \(f(d) = \lfloor \dfrac{k}{d} \rfloor^n\).
最终答案为 \(\sum g(d) \cdot d\).
AT_agc038_c
题意:给定数组 \(A\),求 \(S = \sum\limits_{i=1}^{N}\sum\limits_{j=i+1}^{N}\mathrm{lcm}(A_i,A_j)\) .
令 $g(d) = \sum\limits_{i, j}[(A_i, A_j) = d] \cdot\mathrm{lcm}(A_i,A_j) $.
由于 \(\mathrm{lcm}(a, b) = \dfrac{ab}{\gcd(a, b)}\),则 $\sum\limits_{d = 1}^{\max(A_i)} g(d) - \sum\limits_{i = 1}^nA_i= 2S $
最后对 \(g(d) \cdot d\) 做反演即可。
狄利克雷(Dirichlet)卷积
定义
设 \(f:\mathbb{N^+} \rightarrow \mathbb{R}, \ g:\mathbb{N^+} \rightarrow \mathbb{R}\),则他们的狄利克雷卷积为
性质
-
如果 \(f(n), \ g(n)\) 是积性函数,则 \(h(n) = (f*g)(n)\) 也是积性函数。
证明:
假设 \((p, q) = 1\),则
\[\begin{aligned} h(pq) &= \sum_{\begin{aligned}d_1\mid p \\d_q\mid 2 \end{aligned}} f(d_1d_2) \cdot g(\dfrac{pq}{d_1d_2})\\ &= \sum_{\begin{aligned}d_1\mid p \\d_q\mid 2 \end{aligned}} f(d_1)\cdot f(d_2) \cdot g(\dfrac{p}{d_1})\cdot g(\dfrac{q}{d_1})\\ &= h(p) \cdot h(q) \end{aligned} \] -
\(f = g * 1 \Leftrightarrow g = f * \mu\).
证明:
\[f(n) = \sum_{d \mid n} g(n) \Longleftrightarrow g(n) = \sum_{d\mid n} \mu(n / d)\cdot f(d) \] -
满足交换律与结合律。
\[\begin{aligned} f * g &= g * f \\ (f * g) * h &= f * (g * h) \end{aligned} \] -
\(\epsilon = \mu * 1\).
证明:
设 \(\mu\) 的和函数 \(F(n) = \sum\limits_{d \mid n}\mu(d)\).
\(F(1) = \mu(1) = 1\).
\[\begin{aligned} F(p^k) &= \mu(1) + \mu(p) + \mu(p^2) + \cdots + \mu(p^k) \\ &= 1 + (-1) + 0 + \cdots + 0\\ &= 0 \end{aligned} \]\(F(n) = \prod F(p_i^k) = 0\).
所以 \(\epsilon(n) = F(n)= [n = 1]\).
-
\(id = \phi * 1\).
即证 \(n = \sum\limits_{d \mid n} \phi(d)\).
将 \(m \in [1, n]\) 分类, \(m\) 属于 \(C_d\) 类当且仅当 \((m, n) = d\) 即 \((m / d, n / d) = 1\).
所以 \(C_d\) 的大小为小于 \(n / d\) 且与之互素的正整数个数,恰与 \(\phi(n / d)\) 相等。
\[n = \sum|C_d| = \sum \phi(n/d) = \sum \phi(d) \] -
\(\phi = \mu * id\).
证明:
对于 \(n = p_1^{a_1} \cdots p_k^{a_k}\),令性质 \(a_i\) 表示能够被 \(p_i\) 整除。
\[\begin{aligned} \phi(n) &= N((1 - a_1)\cdots(1 - a_k)) \\ &= \sum_{S \subseteq\{1, \dots, k\}} (-1)^{|S|} \dfrac{n}{\prod\limits _{i \in S}p_i}\\ &= \sum_{d \mid n} [d = p_{x_1}\cdots p_{x_i}] (-1)^i \dfrac{n}{i}\\ &= \sum_{d \mid n} \mu(d) \cdot \dfrac{n}{i}\\ &= (\mu * id)(n) \end{aligned} \]引理:\(\dfrac{\phi(n)}{n} = \sum\limits_{d \mid n}\dfrac{\mu(d)}{d}\)
杜教筛
引入
-
求 \(\Phi(n) = \sum\limits_{i = 1}^{n} \phi(n)\)。
对于欧拉函数,有 \(\phi * I = id\),即 \(\phi(n) = n - \sum\limits_{d \mid n, d < n}\phi(n)\)。
所以
\[\begin{aligned} \sum_{i = 1}^n\phi(i) &= \sum_{i = 1}^n (i - \sum_{d \mid i, d < i}\phi(d))\\ &= \dfrac{n(n + 1)}{2} - \sum_{i = 2}^n\sum_{d \mid i, d < i}\phi(d)\\ &= \dfrac{n(n + 1)}{2} - \sum_{\frac{i}{d} = 2}^n\sum_{d = 1}^{\lfloor\frac{n}{\lfloor\frac{i}{d}\rfloor}\rfloor}\phi(d)\\ &= \dfrac{n(n + 1)}{2} - \sum_{i = 2}^n\sum_{d = 1}^{\lfloor\frac{n}{i}\rfloor}\phi(d)\\ &= \dfrac{n(n + 1)}{2} - \sum_{i = 2}^n\Phi(\lfloor\frac{n}{i}\rfloor)\\ \end{aligned} \]于是只需预处理 \(O(\sqrt{n})\) 个 \(\Phi(\lfloor\dfrac{n}{i}\rfloor)\),就可以算出 \(\Phi(n)\)。
第三第四步将枚举因数化为枚举倍数,是常见减小复杂度的做法。
-
求 \(M(n) = \sum\limits_{i = 1}^{n} \mu(n)\)。
和欧拉函数类似,利用 \(\mu(n) = [n = 1] - \sum\limits_{d \mid n, d < n}\mu(d)\)。
\[\begin{aligned} \sum_{i = 1}^n\mu(n) &= \sum_{i = 1}^n [i = 1] - \sum\limits_{d \mid i, d < i}\mu(d)\\ &= 1 - \sum_{i = 2}^n\sum_{d \mid i, d < i}\mu(d)\\ &= 1 - \sum_{i = 2}^n\sum_{d = 1}^{\lfloor\frac{n}{i}\rfloor}\mu(d)\\ &= 1 - \sum_{i = 2}^nM(\lfloor\frac{n}{i}\rfloor)\\ \end{aligned} \]
推导
对于一个数论函数 \(f(n)\),杜教筛可以在低于线性复杂度内求 \(S(n) = \sum\limits_{i = 1}^nf(i)\).
如果利用整除分块把相等的一起算,就加快了速度。
根据 \(f(n)\) 的性质,构造 \(S(n)\) 关于 \(S(\lfloor\dfrac{n}{i}\rfloor)\) 的递推式,方法如下。
构造两个积性函数 \(h, \ g\),满足 \(h\) 易于求和,\(g\) 易于计算 且\(h = f * g\)。
则 \(h(i) = \sum\limits_{d \mid i}g(d)\cdot f(\dfrac{i}{d})\),对 \(h(i)\) 求和,有
-
公式法求 \(\sum_{i = 1}^n\phi(n)\)。
\(h = id, \ f = \phi, \ g = I\)。
所以 \(\sum\limits_{i = 1}^n id(i) = \sum\limits_{i = 1}^n S(\lfloor\dfrac{n}{d}\rfloor)\),即 \(S(n) = \sum\limits_{i = 1}^n id(i) - \sum\limits_{i = 2}^n S(\lfloor\dfrac{n}{d}\rfloor)\)。
同理,可用 \(\epsilon = \mu * I\) 求出 \(M(n)\)。
实现
对于 \(n < N^{\frac{2}{3}}\) 预处理,否则暴力递归然后记忆化。
复杂度证明:[Auferstanden].
#include<bits/stdc++.h>
#include<bits/extc++.h>
using namespace std;
using uint = unsigned int;
using ll = long long;
constexpr int N = 3e6 + 5, V = 3e6;
__gnu_pbds::gp_hash_table<int, int> Mu;
__gnu_pbds::gp_hash_table<int, ll> Phi;
int mu[N], p[N], v[N], idx;
ll phi[N];
void init() {
phi[1] = mu[1] = 1;
for(int i = 2; i <= V; ++ i) {
if(v[i] == 0) {
mu[i] = -1;
phi[i] = i - 1;
p[++ idx] = i;
}
for(int j = 1; j <= idx && p[j] <= V / i; ++ j) {
v[i * p[j]] = 1;
if(i % p[j] == 0) {
phi[i * p[j]] = phi[i] * p[j];
mu[i * p[j]] = 0;
break;
}
mu[i * p[j]] = -mu[i];
phi[i * p[j]] = phi[i] * (p[j] - 1);
}
}
for(int i = 1; i <= V; ++ i) {
mu[i] += mu[i - 1];
phi[i] += phi[i - 1];
}
}
ll get_Phi(uint n) {
if(n <= V) return phi[n];
if(Phi.find(n) != Phi.end()) return Phi[n];
ll ans = (ll)n * (n + 1) / 2;
for(uint i = 2, j; i <= n; i = j + 1) {
if(n / i == 0) break;
j = n / (n / i);
ans -= get_Phi(n / i) * (j - i + 1);
}
return Phi[n] = ans;
}
int get_Mu(uint n) {
if(n <= V) return mu[n];
if(Mu.find(n) != Mu.end()) return Mu[n];
int ans = 1;
for(uint i = 2, j; i <= n; i = j + 1) {
if(n / i == 0) break;
j = n / (n / i);
ans -= get_Mu(n / i) * (j - i + 1);
}
return Mu[n] = ans;
}
int main() {
cin.tie(0)->sync_with_stdio(0);
init();
int T;
cin >> T;
while(T --) {
uint n; cin >> n;
cout << get_Phi(n) << ' ' << get_Mu(n) << '\n';
}
return 0;
}
矩阵乘法
引入
如果 \(C = AB\),则 \(c_{ij} = \sum\limits_{k = 1}^{n}a_{ik} \cdot b_{kj}\),即 \(A\) 的第 \(i\) 行与 \(B\) 的第 \(j\) 列的点积。
-
假设有 \(n\) 个地点,\(i\) 到 \(j\) 做飞机有 \(a_{ij}\) 种选择,坐火车有 \(b_{ij}\) 种选择。求从 \(i\) 先做飞机再坐火车到 \(j\) 的方案。
枚举中转点 \(k\)。
\(c_{ij} = \sum\limits_{k = 1}^na_{ik}\cdot b_{kj}\),写成矩乘即 \(C = AB\)。
矩阵快速幂优化线性递推
- \(f(n) = a_1f(n - 1) + a_2f(n - 2) + a_3f(n - 3)\).
-
\(f(n) = a_1f(n - 1) + a_2f(n - 2) + C\).
\[\begin{pmatrix} f_n\\ f_{n - 1}\\ C \end{pmatrix} = \begin{pmatrix} a_1 & a_2 & 1\\ 1 & 0 & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} f_{n - 1}\\ f_{n - 2}\\ C \end{pmatrix} \]或
\[\begin{pmatrix} f_n\\ f_{n - 1}\\ 1 \end{pmatrix} = \begin{pmatrix} a_1 & a_2 & C\\ 1 & 0 & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} f_{n - 1}\\ f_{n - 2}\\ 1 \end{pmatrix} \] -
\(f(n) = a_1f(n - 1) + a_2f(n - 2) + c_2n^2 + c_1n + c_0\).
\[\begin{pmatrix} f_n\\ f_{n - 1}\\ (n + 1)^2\\ n + 1\\ 1 \end{pmatrix} = \begin{pmatrix} a_1 & a_2 & c_2 & c_1 & c_0\\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 2 & 1 \\ 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} f_{n - 1}\\ f_{n - 2}\\ n^2\\ n\\ 1 \end{pmatrix} \] -
\(f(n) = a_{11}f(n - 1) + a_{12}g(n - 1), \ g(n) = a_{21}f(n - 1) + a_{22}g(n - 2)\).
\[\begin{pmatrix} f_n\\ g_n\\ \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12}\\ a_{21} & a_{22}\\ \end{pmatrix} \begin{pmatrix} f_{n - 1}\\ g_{n - 1}\\ \end{pmatrix} \] -
若 \(f(n)\) 与 \(g(n)\) 是线性递推的,则 \(h(n) = f(n)\cdot g(n)\) 也能线性递推。
\[\begin{aligned} &\\ f(n) &= f(n - 1) + f(n - 2)\\ &\\ f^2(n) &= f^2(n - 1) + f^2(n - 2) + 2\cdot f(n - 1) \cdot f(n - 2)\\ &\\ f(n - 1) \cdot f(n - 2) &= \begin{cases} f(n - 1)\cdot (f(n - 1) - f(n - 3)) \\ (f(n - 2) + f(n - 3))\cdot f(n - 2) \end{cases}\\ &\\ 2\cdot f(n - 1) \cdot f(n - 2) &= f^2(n - 1) + f^2(n - 2) - f^2(n - 3)\\ &\\ f^2(n) &= 2\cdot f^2(n - 1) + 2\cdot f^2(n - 2) - f^2(n - 3) \end{aligned} \]
例题
CF1117D
题意:有多少长度为 \(n\) 的 \(01\) 串,使得任意极长全 \(0\) 字串的长度都被 \(m\) 整除?(\(n \le 10^{18}, \ m \le 100\))
定义 \(f_{i, 0/1}\) 为长度为 \(i\),结尾为 \(0/1\) 的方案数。
上下相加得到 \(f_i = f_{i - 1} + f_{i - m}\)。
构造矩阵乘法加速递推。
于是有 \(F_{n} = AF_{n - 1} = A^2F_{n - 2} = A^{n - m}F_m\)。
预处理 \(F_m\),时间复杂度 \(O(m + m^3\log n)\)。
注意特判 \(n < m\) 的情况。
NC17890
题意:\(m \times n\) 的方格,每个格子可以填白色或黑色,左右两个不同为白,左右两列不同为全黑,求合法方案数。(\(n\le10^{18}, m \le5\))
先朴素动态规划。
\(f_{i, s}\) 表示第 \(i\) 列状态为 \(s\) 时的方案,'0' 表示白,'1' 表示黑。
考虑 \(s\) 能从哪些 \(s'\) 转移来。
- \(s\ |\ s' = 2^m - 1\)。
- 若 \(s = 2^m - 1\),\(s'\ne 2^m - 1\)。
所以
又可以看成 \(F_n = A\cdot F_{n - 1} = A^{n - 1}\cdot F_1\) 的形式。
CF718C
题意:给定数列 \(\{a\}\),支持两种操作。
- 区间 \([l, r]\) 加 \(x\)。
- 求 \(\sum_{i = l}^rf(a_i)\),\(f(1) = f(2) = 1, \ f(n) = f(n - 1) + f(n - 2)\)。
写成向量的形式
根据递推式,可以写出 \(\vec F(0) = \begin{pmatrix}1\\0\end{pmatrix}\)。
于是可以用 \(\vec{F(a_i)}_{1, 1}\) 来替代原序列,将操作转化为
- 区间 \([l, r]\) 左乘 \(\begin{pmatrix} 1 & 1\\ 1 & 0\\ \end{pmatrix}^x\)。
- 查询 \(\sum_{i = l}^r\vec{F(a_i)}_{1, 1}\)。
用一个 \(2 \times 1\) 的向量表示线段树的节点,\(2 \times 2\) 的向量表示懒标记,维护区间矩阵乘法。
P6327 区间加区间 sin 和
题意:给出一个长度为 \(n\) 的整数序列 \(a_1,a_2,\ldots,a_n\),进行 \(m\) 次操作,操作分为两类。
操作 \(1\):给出 \(l,r,v\),将 \(a_l,a_{l+1},\ldots,a_r\) 分别加上 \(v\)。
操作 \(2\):给出 \(l,r\),询问 \(\sum\limits_{i=l}^{r}\sin(a_i)\)。
\(\sin(x + v)\) 和 \(\cos(x + v)\) 都是线性递推的。
线段树维护即可。
斐波*
题意:斐波那契数列 \(\{fib\}\) 满足
\(S\) 是一个可重集合 \(\left\{s_1,s_2,...,s_{|S|}\right\}\)。
\(f(S)\) 定义为
支持两种操作。
- 把 \(a_p\) 变为 \(v\)。
- 计算 \(\sum_{i=l}^{r}\sum_{j=i}^{r}f(\left\{a_i,a_{i+1},..,a_j\right\})\) 。
定义 \(g(n) = fib^2(n)\)。
证明参考上文 矩阵快速幂优化线性递推.5。
写成向量形式。
虽然 \(\vec{G(0)}\) 不存在,但仍可通过递推式求出 \(\vec{G(0)} = \begin{pmatrix}0\\1\\1\\\end{pmatrix}\)。
用向量的第一个元素表示答案。
往集合里新增一个元素 \(a\)。
其中 \(I\) 是单位矩阵。
所以
将 \((I + A^{a_i})\) 视作元素 \(v_i\)。
题目要求的 \(\sum_{i=l}^{r}\sum_{j=i}^{r}f(\left\{a_i,a_{i+1},..,a_j\right\})\) 即
即区间 \([l, r]\) 内所有子区间的元素积之和。
考虑分治。
将 \([l, r]\) 分为 \([l, mid]\) 和 \([mid + 1, r]\)。
讨论贡献来源,令 \(\{l, r\}\) 表示 \(\prod_{i = l}^r v_i\)。
- 子区间单独属于左区间或右区间,向下递归。
- 子区间跨块,贡献为 \(\sum\limits_{i = l}^{mid}\{i, mid\} \cdot \sum\limits_{i = mid + 1}^{r} \{mid + 1, i\}\).
具体实现用线段树内维护 \(4\) 个信息。
对于代表区间 \([l, r]\) 的节点。
- \(ans\) 表示 \([l, r]\) 的答案。
- \(self = \prod_{i = l}^r v_i\)
- \(left = \sum_{i = l}^r\{l, i\}\)
- \(right = \sum_{i = l}^r\{i, r\}\)
struct Node {
Matrix ans, self, l, r;
Node() { self = I; }
void operator = (Matrix x){
ans = self = l = r = x;
}
friend Node operator + (Node L, Node R) {
Node x;
x.ans = L.ans + R.ans + L.r * R.l;
x.self = L.self * R.self;
x.l = L.l + R.l * L.self;
x.r = R.r + L.r * R.self;
return x;
}
} t[N << 2];
线性方程组
Gauss-Jordan 消元法
思想很简单,即
- 选主元。
- 选主元不为零的行为主行。
- 用主行消去主行外的所有主元。
判断无解或无穷解。
如果最终增广矩阵如下。
最后一行系数矩阵为零,而增广矩阵非零,无解。
如果增广矩阵也为零呢?
可以得到
其中 \(x_2, \ x_4 \in \R\) ,有无穷多组解,\(x_2, \ x_4\) 确定,则解确定。
增广矩阵每一行第一个非零元对于的变量称为 首变量(lead variable),化简过程种跳过的变量称为 自由变量(free variable)。
因此 \(x_1, x_3, x_5\) 为首变量,\(x_2, x_4\) 为自由变量。
时间复杂度 \(O(n^3)\)。
#include<bits/stdc++.h>
using namespace std;
using db = double;
constexpr int N = 105;
db a[N][N];
int n;
bool neq(db x, db y) {
return fabs(x - y) > 1e-6;
}
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> n;
for(int i = 1; i <= n; ++ i) {
for(int j = 1; j <= n + 1; ++ j) {
cin >> a[i][j];
}
}
int cur = 1;
for(int k = 1; k <= n; ++ k) { \\ 选主元
for(int i = cur; i <= n; ++ i) {
if(neq(a[i][k], 0)) { \\ 选主行
for(int j = k; j <= n + 1; ++ j) {
swap(a[cur][j], a[i][j]);
}
break;
}
}
if(neq(a[cur][k], 0)) { \\ 消元
db x = a[cur][k];
for(int j = k; j <= n + 1; ++ j) {
a[cur][j] /= x;
}
for(int i = 1; i <= n; ++ i) {
if(i == cur) continue;
db x = a[i][k];
for(int j = k; j <= n + 1; ++ j) {
a[i][j] -= x * a[cur][j];
}
}
++ cur; \\ 主行移至下一行
}
}
for(int i = cur; i <= n; ++ i) {
if(neq(a[i][n + 1], 0)) {
cout << -1;
exit(0);
}
}
if(cur != n + 1) {
cout << 0;
}
else {
for(int i = 1; i <= n; ++ i) {
cout << "x" << i << "=" << fixed << setprecision(5) << a[i][n + 1] << '\n';
}
}
return 0;
}
异或方程组
异或可看成模 \(2\) 意义下的加法,写法与加法无异。
有几个优化的点。
bitset<N> a[N]替代系数矩阵。- 交换用
swap(a[i], a[cur])。 - 消元用
a[i] ^= a[cur])。
时间复杂度 \(O(\dfrac{n^3}{w})\)。
例题
POJ1222
题意:\(5 \times 6\) 的方格,改变一盏灯的状态会改变周围所有灯的状态,给出一种开关方案使得所有灯熄灭。
令 \(x_{i, j} = 0 / 1\) 表示 \((i, j)\) 有无操作。
如果 \((i, j)\) 初状态为 \(a_{i, j}\),则达到末状态需要满足 \(a_{i, j} \oplus\)
对 \(30\) 个未知数与 \(30\) 个方程进行高斯消元。
如果处理无穷多组解的情况?将自由变量全赋值为 \(0\),第 \(i\) 行的首变量即列的增广一列的值。
CF1344F
题意:一个包含三原色 RYB 的序列混合的结果定义为:
- 如果序列开头两项颜色相同,将这两项删去。
- 如果序列开头两项颜色不同,将这两项替换为与这两种颜色不同的颜色。
- 特别地,如果序列为空,则混合的结果是白色
W。
有一个长为 \(n\) 的颜色序列(某些位置为空),给出 \(k\) 个操作:
mix:选择一个子序列和混合时的顺序(忽略空位置),给出其混合后的结果。RY:选择一个子序列,将所有R变为Y,所有Y变为R,B和空位置不变。RB:选择一个子序列,将所有R变为B,所有B变为R,Y和空位置不变。YB:选择一个子序列,将所有Y变为B,所有B变为Y,R和空位置不变。
你需要根据 mix 操作的信息确定一种可能的原序列。保证 \(n, k \leqslant 10^3\)。


将 WRYB 依次赋值为 \(0, 1, 2, 3\),可以发现 mix 操作即对取出元素做异或。
将 \((00)_2, (01)_2, (10)_2, (11)_2\) 表示为 \((b_ia_i)_2\)。
RY,交换选定数的 \(a_i, b_i\)。RB,\(b_i \leftarrow a_i \oplus b_i\)。YB,\(a_i \leftarrow a_i \oplus b_i\)。
动态维护当前的 \(a_i\) 和 \(b_i\) 与初始值的关系,设 \(i\) 初始为 \((b_0a_0)_2\)。
- \(t_i = (00) \iff a_i = 0\)。
- \(t_i = (01) \iff a_i = a_{i_0}\)。
- \(t_i = (10) \iff a_i = b_{i_0}\)。
- \(t_i = (11) \iff a_i = a_{i_0} \oplus b_{i_0}\)。
\(b_i\) 同理维护一个 \(t_i'\)。
把 \(a_{i_0}\),\(b_{i_0}\) 表示为 \(2n\) 个未知数。
对于一次 mix 操作,可以对分别对当前 \(\{a_i\}\) 和\(\{b_i\}\) 异或得到关于 \(a_{i_0}\),\(b_{i_0}\)的两组方程。
高斯消元求出所有\(a_{i_0}, \ b_{i_0}\)。
线性基
引入
线性基即高中数学向量基底拓展到 \(n\) 维的情况。
线性基内元素线性无关,即不能互相表示。
线性基可以表示出任意当前线性空间内的元素。
异或线性基
对于一组基 \(\{b\}\),其内元素不能通过异或运算互相表示。
-
高斯消元求线性基
求解 \(\{a\} = {1, 3, 4, 6, 7}\) 的一组基底。
把一个 \(n\) 位二进制数看作 \(n\) 维向量。
\[\begin{bmatrix} 1 & 0 & 0\\ 1 & 1 & 0\\ 0 & 0 & 1\\ 0 & 1 & 1\\ 0 & 1 & 1\\ \end{bmatrix} \]执行高斯消元。
\[\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ 0 & 0 & 0\\ 0 & 0 & 0\\ \end{bmatrix} \]剩下 \(3\) 个非零元素 \(\{1, 2, 4\}\)即为 \(\{a\}\) 的一组基。
显然可用 \(1, 2, 4\) 表示出 \(3, 6, 7\) 却无法互相表示。
引理:大小为 \(sz\) 的基底能组成 \(2^{sz}\) 个不同的数。
证明:高斯消元得到的基底互不相交,任意组合互不相同。
-
在线求线性基
高斯消元是离线的,复杂且有局限性。
设 \(b_i\) 为基底中最高位为 \(i\) 的元素。
用如下方法插入新元素,其实际意义与高斯消元无异。
void insert(int x) { for(int i = 30; i >= 0; -- i) { if(x >> i & 1) { if(b[i] == 0) { b[i] = x; return; } x ^= b[i]; } } } -
求线性基内得到的最大(小)元素
高斯消元得到的基底元素交集为空,全部异或起来即最大值。
在线插入法可以如下贪心:
int get_max() { int cur = 0; for(int i = 30; i >= 0; -- i) { cur = max(cur, cur ^ b[i]); } return cur; } -
判断某个元素是否在线性空间内存在
低位操作不会影响高位,从高到低贪心。
bool exist(int x) { int cur = 0; for(int i = 30; i >= 0; -- i) { if((x >> i & 1) != (cur >> i & 1)) { cur ^= b[i]; } } return x == cur; }
例题
CF1101G
题意:
给定 \(\{a_i\}\),试将其划分为尽可能多的非空子段,满足每一个元素出现且仅出现在其中一个子段中,且在这些子段中任取若干段,它们包含的所有数的异或和不能为\(0\).
如果不存在方案输出 \(-1\),否则输出所有合法的划分方案中最大的划分数。
表示成前缀异或。
设 \(i_1, i_2, \dots i_k\) 为划分点。
则 \(\{s_{i_2}\oplus s_{i_1 - 1}, \dots s_{i_k}\oplus s_{i_{k - 1} - 1}\}\) 互相组合不能表示出零。
表示出零,当且仅当存在元素能被其他元素表示。
所以 \(\{s_{i_2}\oplus s_{i_1 - 1}, \dots s_{i_k}\oplus s_{i_{k - 1} - 1}\}\) 的线性基(等效于 \(\{s_i\}\) 的线性基)为极大符合条件集合。
线性基的大小唯一确定,无解的情况为 \(s_n = 0\)。
形式幂级数
多项式与形式幂级数
- 多项式:\(A(x) = \sum_{i = 0}^na_ix^i\)。
- 形式幂级数:\(A(x) = \sum_{i \ge 0}a_ix^i\)。
其中 \(a_i \in K\),\(K\) 是一个域,通常考虑 \(K = \mathbb{R}\) 或 \(K = \mathbb{Z}_{p}\)。
注意这里的 \(x\) 可以理解为独立于域 \(K\) 的一个符号。
形式幂级数的运算
设 \(A(x) = \sum_{i \ge 0} a_ix^i, \ B(x) = \sum_{i \ge 0} b_ix^i\)。
- 加法:\(A(x) + B(x) = \sum_{i \ge 0} (a_i + b_i)x^i\)。
- 减法:\(A(x) - B(x) = \sum_{i \ge 0} (a_i - b_i)x^i\)。
- 乘法:\(A(x)\times B(x) = \sum_{k \ge 0} (\sum_{i = 0}^ka_i b_{k - i})x^k\)。
可以验证,形式幂级数在以上定义的 \(+, -, \times\) 下形成一个环。
记号:记形式幂级数(或多项式)\(A(x)\) 的 \(x^n\) 项的系数为 \([x^n]A(x)\)。
形式幂级数的逆元
-
形式幂级数的逆元:\(A(x)B(x) = 1\)。
-
逆元存在的条件:\([x^0]A(x) \neq 0\)。
-
暴力计算的方法:递推。
设 \(A(x) = a_0 + a_1x + a_2x^2 +\cdots, \ B(x) = b_0 + b_1x + b_2x^2 + \cdots\)。
则 \(A(x)B(x) = a_0b_0 + (a_0b_1 + a_1b_0)x + \cdots + (a_0b_n + a_1b_{n - 1} + \cdots + a_nb_0)x^n + \cdots\)。
\(A(x)B(x) = 1\) 当且仅当
\[\begin{cases} a_0b_0 = 1\\ a_0b_1 + a_1b_0 = 0\\ \vdots\\ a_0b_n + a_1b_{n - 1} + \cdots + a_nb_0 = 0\\ \vdots \end{cases} \]所以 \(b_0 = a_0^{-1}\),\(b_n = (a_1b_{n - 1} +\cdots+ a_nb_0) \cdot a_0^{-1}\)。
常见的逆
-
\(A(x) = 1 + x + x^2 + \cdots\) 和 \(B(x) = 1 - x\),即 \(A(x) = \dfrac{1}{1 - x}\)。
-
\(A(x) = 1 + ax + a^2x^2 + \cdots\) 和 \(B(x) = 1 - ax\),即 \(A(x) = \dfrac{1}{1 - ax}\)。
-
\(A(x) = 1 + f(x) + f^2(x) + \cdots\) 和 \(B(x) = 1 - f(x)\),即 \(A(x) = \dfrac{1}{1 - f(x)}\)。
-
\(A(x) = {k - 1\choose 0} + {k \choose1}x + {k + 1\choose2}x^2 + \cdots\) 和 \(B(x) = (1 - x)^k\),即 \(A(x) = \dfrac{1}{(1 - x)^k}\)。
\(A(x) = (1 + x + x^2 + \cdots)^k = \dfrac{1}{(1 - x)^k}\)。
即不定方程 \(x_1 + x_2 + \cdots+ x_k = n, \ \forall x_i \ge0\) 的常生成函数。
同时,我们知道该方程的解的数量为 \(n + k - 1\choose k - 1\)。
所以有 \([x^n]A(x) = {n + k - 1\choose k - 1} = {n + k - 1\choose n}\)。
常生成函数(Ordinary Generating Function)
定义
一个数列 \(\{a_n\}\) 对应的常生成函数为 \(A(x) = \sum_{n \ge 0} a_nx^n\)。
-
两种物体,其中取 \(i\) 个第 \(1\) 种物体的方案数为 \(a_i\),取 \(j\) 个第 \(2\) 种物体的方案数为 \(b_i\),求取 \(k\) 个物体的方案数 \(c_k\)。
\[C(x) = \sum_{k \ge 0} c_k = \sum_{k \ge 0} \sum_{i = 0}^ka_ib_{k - i} = A(x) B(x) \]所以 \(c_k = [x^k](A(x)B(x))\)。
-
取 \(n\) 个水果,苹果个数必须是偶数,香蕉个数必须是 \(3\) 的倍数,草莓个数不超过 \(5\),求方案数。
令 \(a_i\) 为取 \(i\) 个苹果的方案数,则 \(a = \{1, 0, 1, 0, 1\cdots\}\)。
所以
- \(A(x) = 1 + x^2 + x^4 + \cdots\)。
- \(B(x) = 1 + x^3 + x^6 + \cdots\)。
- \(C(x) = 1 + x^2 + x^3 + x^4 + x^5\)。
取 \(n\) 个水果的方案为 \(A(x)B(x)C(x)\) 第 \(x^n\) 项的系数。
可以先 \(O(n^2)\) 求 \(A(x)\) 与 \(B(x)\) 乘积的前 \(n\) 项,再 \(O(n^2)\) 求 \(A(x)B(x)\) 与 \(C(x)\) 乘积的前 \(n\) 项。
不定方程的解的数量
求不定方程 \(x_1 + x_2 = n\) 的解的数量,其中 \(l_1 \le x_1 \le r_1, \ l_2 \le x_2 \le r_2\)。
令数列 \(\{a_n\}\) 表示 \(x_1 = n\) 的解的数量,则 \(\forall n \in [l_1, r_1], \ a_n = 1\)。
那么 \(\{a_n\}\) 的常生成函数 \(F_1(x) = \sum_{i = l_1}^{r_1} x^i\)。
所以解的数量为 \([x^n] (F_1(x)F_2(x))\)。
同理,推广到 \(k\) 元不定方程,解的数量为 \([x^n](\prod F_i(x))\) 。
拓展:求 \(x_1 + 2x_2 + 3x_3 = n\) 的正整数解个数。
\(F_1(x) = \sum_{n \ge 1} x^n = x + x^2 + x^3 + \cdots\)。
\(F_2(x) = \sum\limits_{n \ge 1, \ 2 \mid n} x^n = x^2 + x^4 + x^6 + \cdots\)。
\(F_3(x) = \sum\limits_{n \ge 1, \ 3 \mid n} x^n = x^3 + x^6 + x^9 + \cdots\)。
相乘即可。
定理
设 \(S = \{a_1, a_2, a_3, \dots a_k\}\),且 \(a_i\) 可以取的次数集合为 \(M_i\),记 \(F_i = \sum\limits_{u \in M_i}x^u\),则从 \(S\) 中取 \(n\) 个元素的方案 \(g(n)\) 的常生成函数 \(G(x) = \sum_{i \ge 0}g(i)x^i\),满足
递推关系
-
斐波那契数列满足 \(a_0 = 0, a_1 = 1, a_2 = 1, a_n = a_{n - 1} + a_{n - 2}\),求其常生成函数。
\[\begin{aligned} \\ A(x) &= a_0 + a_1x + a_2x^2 + a_3x^3 +\cdots\\ \\ &= a_0 + a_1x + (a_0 + a_1)x^2 + (a_1 + a_2)x^3 + \cdots\\ \\ &= x + (a_0x^2 + a_1x^3 + \cdots) + (a_1x^2 + a_2x^3 + \cdots)\\ \\ &= x + xA(x) + x^2A(x) \end{aligned} \]所以 \(A(x) = \dfrac{x}{1 - x - x^2}\)。
-
利用常生成函数,求解斐波那契通项公式。
待定系数解得
所以
-
假设数列 \(\{a_n\}\) 存在递推关系 \(a_n = c_1a_{n - 1} + c_2a_{n - 2} + \cdots + c_ka_{n - k}\),求其常生成函数。
\[\begin{aligned} A(x) &= a_0 + a_1x + \cdots + a_{k - 1}x^{k - 1} + \sum_{n \ge k}(c_1a_{n - 1} +\cdots + c_ka_{n - k})x^n\\ \\ &= a_0 + \cdots + a_{k - 1}x^{k - 1} + c_1x(A(x) -\sum_{i \le k - 2}a_ix^i) + c_2x^2(A(x) - \sum_{i \le n - 3}a_ix^i) + \cdots + c_kx^kA(x)\\ \\ &= (c_1x + \cdots + ck_x^k)A(x) + B(x) \end{aligned} \]\(A(x)\) 可以表示为 \(\dfrac{B(x)}{1 - (c_1x + \cdots + ck_x^k)}\)。
若想将 \(A(x)\) 还原为 \(\sum a_ix^i\) 的形式,待定系数 \(A(x) = B(x) \sum \dfrac{v_i}{1 - u_ix}\)。
例题
A-背包
那么 \([x^n]G(x) = [x^{n - 1}]\dfrac{1}{(1 - x)^4} = \begin{pmatrix}n + 2\\ 3\end{pmatrix} = \dfrac{n(n + 1)(n + 2)}{6}\)。
CF451E
题意:\(n\) 种花,分别 \(f_1, f_2\dots,f_n\) 个,求取 \(s\) 朵花的方案数,\(n \le 20, s \le 10^{18}\)。
不妨令 \(F(x) = \prod (1 - x^{f_i + 1})\)。
则
\(n\) 很小,暴力展开 \(F(x)\) 的系数。
P6078 [CEOI2004] Sweets
题意:\(n\) 种糖,分别 \(m_1, m_2\dots,m_n\) 个,求吃至少 \(a\),不多于 \(b\) 的方案数 ,\(n \le 10, a \le 10^7\)。
\(F(x) = \prod (1 - x^{m_i + 1})\)。
引理:\(\sum_{i = a}^b\begin{pmatrix}i\\j\end{pmatrix} = \begin{pmatrix} b + 1\\ j + 1\end{pmatrix} - \begin{pmatrix} a\\ j + 1\end{pmatrix}\)。
证明:
其中
所以 \(\sum_{i = a}^b\begin{pmatrix}i\\j\end{pmatrix} = \begin{pmatrix} b + 1\\ j + 1\end{pmatrix} - \begin{pmatrix} a\\ j + 1\end{pmatrix}\)。
所以原问题答案为
题目模数 \(P = 2004\) 不好处理。
对于模数非质数的除法,可以先把模数乘上除数,再将运算结果除以除数得到答案。
不妨先令答案乘上 \(n!\),同时 \(P \leftarrow P \cdot n!\),最后再除以 \(n!\)。
指数生成函数(Exponential Generating Function)
定义
一个数列 \(\{a_n\}\) 的指数生成函数为 \(A(x) = \sum\limits_{n \ge 0}a_n\dfrac{x^n}{n!}\)。
对于 \(\{a_n\} = \{1, 1, 1, \cdots\}\),\(A(x) = 1 + \dfrac{x}{1!} + \dfrac{x^2}{2!} + \dfrac{x^3}{3!} + \cdots = e^x = \exp (x)\)。
-
两种物体,其中取 \(i\) 个第 \(1\) 种物体的方案数为 \(a_i\),取 \(j\) 个第 \(2\) 种物体的方案数为 \(b_i\),求取 \(k\) 个物体并排成一排的方案数 \(c_k\)。
\(c_k = \sum\limits_{i = 0}^k a_ib_{k - i}\dfrac{k!}{i!(k - i !)}\)。
\(C(x) = \sum\limits_{k \ge 0} \dfrac{c_k}{k!} = \sum\limits_{k \ge 0}\sum\limits_{i = 0}^k \dfrac{a_i}{i!}\cdot \dfrac{b_{k - i}}{(k - i !)} = A(x) B(x)\)。
-
用 \(1, 2, 3, 4\) 组成 \(6\) 位数,每个数字出现次数不得大于 \(2\),求不同的六位数个数。
\(\{a\} = \{1, 1, 1, 0, 0 \cdots\}, \ F(x) = 1 + \dfrac{x}{1!} + \dfrac{x^2}{2!}\)。
\(G(x) = F^4(x)\)。
则不同的六位数个数为 \(6! [x^6]G(x)\)。
定理
设 \(S = \{a_1, a_2, a_3, \dots a_k\}\),且 \(a_i\) 可以取的次数集合为 \(M_i\),记 \(F_i = \sum\limits_{u \in M_i}x^u\),则从 \(S\) 中取 \(n\) 个元素排成一排的方案 \(g(n)\) 的指数生成函数 \(G(x) = \sum_{i \ge 0}g(i)\dfrac{x^i}{i!}\),满足
公式(定义)
- \(\exp(x) = 1 + \dfrac{x}{1!} + \dfrac{x^2}{2!} + \cdots = \sum_{n \ge 0}\dfrac{x^n}{n!}\)。
- \(\exp(ax) = 1 + \dfrac{ax}{1!} + \dfrac{a^2x^2}{2!} + \cdots = \sum_{n \ge 0}\dfrac{a^nx^n}{n!}\)。
- \(\exp(f(x)) = 1 + \dfrac{f(x)}{1!} + \dfrac{f^2(x)}{2!} + \cdots = \sum_{n \ge 0}\dfrac{f^n(x)}{n!}\)。
- \(\dfrac{\exp(x) + \exp(-x)}{2} = \sum_{n \ge 0} [2 \mid n] \dfrac{x^n}{n!}\)。
- \(\dfrac{\exp(x) - \exp(-x)}{2} = \sum_{n \ge 0} [2 \nmid n] \dfrac{x^n}{n!}\)。
例题
POJ3734
题意:\(n\) 个格子排成一列,每个格子可以被涂成红、黄、蓝或绿,偶数个格子是红和绿,求方案数。
CF891E
题意: \(n\) 个数,\(k\) 次操作,每次随机选择一个数 \(x \in [1,n]\),把 \(a_x\) 减一,并将答案增加除 \(a_x\) 外所有数的乘积。
求最终答案的期望,对 \(10^9 + 7\) 取模。
第一次操作对答案的贡献为
以此类推,当前轮的贡献为当前所有数之积减去下一轮所有数之积。
最终结果可以表示为 \(\prod a_i - \prod(a_i - x_i)\),\(x_i\) 为 \(i\) 被操作的次数。
所以后项的期望值
令 \(F_i(x) = \sum_{j \ge 0} \dfrac{a_i - j}{j!}x^j\)。
则
设 \(G(x) = \prod(a_i - x)\)。
那么
由于 \(i > n\) 时 \(G(x)\) 系数为 \(0\),所以枚举到 \(\min(n, k)\) 即可。
Catalan 数
推导
\(n + 1\) 个数相乘 \(x_0x_1x_2\cdots x_n\),求其结合顺序的方案数。如 \(n = 3\) 时,有 \(5\) 种方案:
枚举最后一步在哪划分,得到递推式
考虑其生成函数
则 \(C(x) = \dfrac{1 \pm \sqrt{1 - 4x}}{2x}\)。
若满足 \(g^2(x) = f(x)\),则 \([x^0]g(x) > 0\) 的记作 \(\sqrt {f(x)}\),\([x^0]g(x) < 0\) 的记作 \(-\sqrt {f(x)}\)。
由于 \(4x\) 不存在逆元(常数项为 \(0\)),必然被分子约掉。
而分子上如果取正号,则常数项不为 \(0\),不能约去常数项为 \(0\) 的式子。
所以 \(C(x) = \dfrac{1 - \sqrt{1 - 4x}}{2x}\)。
利用广义二项式定理,展开
广义组合数:\(\alpha \in \mathbb{R}, \ \begin{pmatrix}\alpha\\0\end{pmatrix} = 1,\ \begin{pmatrix}\alpha\\k\end{pmatrix} = \dfrac{\alpha(\alpha - 1) \cdots(\alpha - k + 1)}{k!}\)。
广义二项式定理:\((x + y)^\alpha = \sum\limits_{k = 0}^{+\infty}\begin{pmatrix}\alpha\\k\end{pmatrix}x^{\alpha - k}y^k\)。
可以推出卡特兰数的通项公式
多项式的表示形式
系数表示与点值表示
假设 \(f(x)\) 是一个 \(n\) 次多项式,则 \(f(x)\) 的系数表示为 \(f(x) = a_nx^n + a_{n - 1}x^{n - 1} + \cdots + a_0\)
\(f(x)\) 的点值表示为 \((x_0, f(x_0)), \ (x_1, f(x_1)), \dots, (x_n, f(x_n))\),其中 \(\forall i \neq j, \ x_i \neq x_j\)。
-
\(n + 1\) 个点值可以表示一个 \(n\) 次多项式。
-
在点值表示下 \(n\) 次多项式的乘法复杂的为 \(O(n)\)。
设 \(h(x) = f(x) \cdot g(x)\),则 \(\forall i \in [0, n], \ h(x_i) = f(x_i) \cdot g(x_i)\)。
复数与单位根
复数的指数形式
\(a + bi = re^{i\theta}\),其中 \(r = \sqrt {a^2 + b^2}, \ \tan \theta = \dfrac{b}{a}\)。
欧拉公式:\(e^{ix} = \cos x + i\sin x\)。
单位根
\(x^n = 1\) 在复数域上的根称为 \(n\) 次单位根。\(n\) 次单位根有 \(n\) 个,形式为 \(\omega_{n}^k = e^{i\frac{2k\pi}{n}}\)。
单位根在复平面上等分单位圆。
单位根的性质:
- \(\omega_n^k = \omega_{2n}^{2k}\)。
- \(\omega_{2n}^{k + n} = -\omega_{2n}^{k}\)
快速傅里叶变换(Fast Fourier Transform)
离散傅里叶变换(Discrete Fourier Transform)
将多项式 \(A(x) = a_0 + a_1x + \dots + a_{n - 1}x^{n - 1}\) 转化为其点值形式 \((\omega_n^k, \ A(\omega_n^k)), \ (k = 0, 1, \dots, n - 1)\)。
不妨令 \(n\) 为 \(2\) 的整次幂。
把原式拆成奇偶两部分,即 \(A(x) = (a_0 + a_2x^2 + \cdots + a_{n - 2}x^{n - 2}) + (a_1 + a_3x^3 + \cdots + a_{n - 1}x^{n - 1})\)。
令 \(B(x) = a_0 + a_2x + \cdots + a_{n - 2}x^{n / 2 - 1}, \ \ C(x) = a_1 + a_3x + \cdots + a_{n - 2}x^{n / 2 - 1}\)。
则 \(A(x) = B(x^2) + xC(x^2)\)。
对于 \(k \in [0, n / 2 - 1]\)
对于另一半的点值,可用 \(A(\omega_n^{k + n / 2})\) 表示,即
具体的讲,当 \(n = 8\) 时,各项存在如下关系:
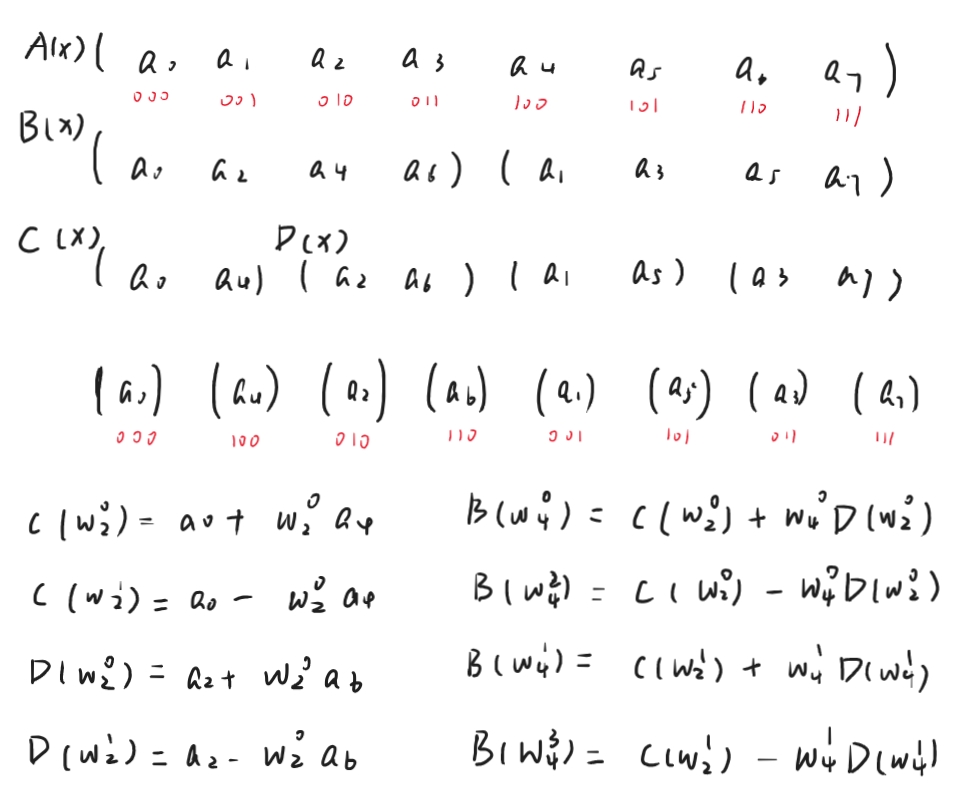
\(T(n) = 2T(n / 2) + O(n)\)。
可以直观看出,以这种方式将系数表示转化为点表示的时间复杂度为 \(O(n \log n)\)。
对于具体实现
-
分治(递归,常数大)。
-
蝴蝶变换(bit-reversal permutation)(非递归,常数小)。
观察上图第一行和最后一行各项的二进制表示,互相颠倒。
因此可以预处理最后一行的系数,自下而上递推。
逆离散傅里叶变换(Inverse DFT)
将多项式的点值表示 \((\omega_n^k, \ b_k), \ (k = 0, 1, \dots, n - 1)\) 转化为其系数表示 \(A(x) = a_0 + a_1x + \dots + a_{n - 1}x^{n - 1}\)。
设 \(n \times n\) 的矩阵 \(\Omega\),其中 \(\Omega_{i, j} = \omega_n^{ij}\),设向量 \(a = (a_0, a_1, \dots, a_{n - 1}), \ b = (b_0, _1, \dots, b_{n - 1})\)。
则 IDFT 相当于求解方程 \(\Omega a = b\)。
如果我们能够求出 \(\Omega\) 的逆,则 \(a = \Omega^{-1}b\)。
设
其中
相当于等比数列求和
令 \(\overline\Omega\) 满足 \(\overline\Omega_{i, j} = \omega^{-ij}\),有 \(\overline\Omega\cdot\Omega = nI\),因此
相当于给定 \(B(x) = b_0 + b_1x + \cdots + b_{n - 1}x^{n - 1}\),求点值 \(a_k = B(\omega_n^{-k}), \ (0 \le k < n)\)。
例题
A * B Problem Plus
题意:给定 \(a, \ b\),求 \(a \times b\),\(a, \ b < 10^{50001}\)(范围可以更大)。
将 \(a\) 看作 \(a_0 + a_110^1 + a_210^2 + \cdots\),fft 后再处理进位。
SP8372 TSUM
题意:给定长度为 \(N\) 的数列 \(s\),对于任意可能存在的 \(V\),求满足 \(s_i + s_j + s_k = V, \ \ i < j < k\) 的对数,\(|s_i| \le 20000, \ N \le 40000\)。
构造多项式 \(A(x) = \sum x^{s_i}\)。
那么 \(\sum\limits_{i}\sum\limits_{j}\sum\limits_{k}[s_i + s_j + s_k = V] = [x^V]A^3(x)\)。
这样求得的数对不一定满足偏序关系,也不一定互不相同。
偏序关系很好处理,最后将答案除上 \(3!\) 即可。
现要除去存在位置相同的数对,考虑容斥。
性质 \(a_1: i = j\),性质 \(a_2: i = k\),性质 \(a_3:j = k\)。
-
减去满足三个性质中一个的方案。
钦定两个位置相等。
令 \(B(x) = \sum x^{2s_i}\),产生的方案为 \([x^V](A(x)B(x))\)。
-
加上满足三个性质中两个的方案。
\(i = j = k\)。
令 \(C(x) = \sum x^{3s_i}\),这部分的方案为 \([x^V]C(x)\)。
-
减去满足三个性质中三个的方案。
与第二部分相同。
则最终答案 \(D(x) = A^3(x) - 3B(x) + 2C(x)\)。
可以先对 \(A(x), \ B(x), \ C(x)\) 分别做 dft,计算出 \(D(x)\) 的点值,最后再对 \(D(x)\) 做 idft。
FFT 在字符串匹配中的应用
普通的单模式串匹配
问题概述:给定模式串 \(a\)(长度为 \(m\))、文本串 \(b\)(长度为 \(n\)),求所有位置 \(x\),满足 \(B\) 串以 \(x\) 结尾的连续 \(m\) 个字符与 \(a\) 串完全相同。
定义匹配函数 \(C(x, y) = [a_x - b_y]^2\),当 \(C(x, y) = 0\) 时则称 \(a\) 的第 \(x\) 个字符与 \(B\) 的第 \(y\) 个字符匹配。
定义完全匹配函数 \(P(x) = \sum\limits_{i = 0}^{m - 1}[a_i - b_{(x -m + i + 1)}]^2\)。
当且仅当 \(P(x) = 0\) 时以 \(x\) 结尾的连续 \(m\) 个字符与 $$ 匹a配。
令 \(s\) 串满足 \(s_i = a_{(m - i - 1)}\),即 \(a\) 串的翻转。
于是 \(P(x) = \sum\limits_{i = 0}^{m - 1}[s_{(m - i + 1)} - b_{(x -m + i + 1)}]^2\)。
暴力展开:\(P(x) = \sum\limits_{i = 0}^{m - 1} s_{(m - i + 1)}^2 + \sum\limits_{i = 0}^{m - 1}b_{(x -m + i + 1)}^2 - \sum\limits_{i = 0}^{m - 1}2\cdot s_{(m - i + 1)}b_{(x - m + i + 1)}\)。
第一项为常数。
第二项可以预处理 \(f(x) = \sum_{i = 0}^xb_i^2\),计算 \(f(x) - f(x - m)\)。
第三项等效于求 \(g(x) = \sum\limits_{i + j = x}s_ib_j\)。
则 \(P(x) = T + f(x) - f(x - m) - 2g(x)\)。
把字符串当作多项式,即 \(B(x) = b_0 + b_1x + b_2x^2 + \cdots\)。
则 \(g\) 为 \(S\) 与 \(B\) 的卷积。
最后检验多项式 \(P\) 有多少系数为 \(0\) 的项。
带通配符的单模式串匹配
问题概述:给定模式串 \(a\)(长度为 \(m\)),文本串 \(b\)(长度为 \(n\)),串的某些字符是 “通配符”(可以与任意字符匹配)。求所有位置 \(x\),满足 \(b\) 串以 \(x\) 结尾的连续 \(m\) 个字符与 \(a\) 串完全相同。
总结思路:
- 定义匹配函数。
- 定义完全匹配函数。
- 快速计算每一位的完全匹配函数(翻转模式串化为卷积)。
设通配符的数值为 \(0\)。
定义匹配函数 \(C(x, y) = [a_x - b_y]^2a_xb_y\)。
则完全匹配函数 \(P(x) = \sum\limits_{i = 0}^{m - 1}[a_i - b_{(x -m + i + 1)}]^2a_ib_{(x - m + i + 1)}\)。
将 \(a\) 翻转,\(P(x) = \sum\limits_{i = 0}^{m - 1}[s_{(m - i + 1)} - b_{(x -m + i + 1)}]^2\cdot s_ib_{(x - m + i + 1)}\)。
暴力展开:
把右边写成多项式乘积的形式,则
例题
P4173 残缺的字符串
模板题。
#include<bits/stdc++.h>
using namespace std;
using namespace numbers;
using ll = long long;
constexpr int N = 6e5 + 5, tot = 1 << 19;
struct Complex {
double x, y;
Complex operator + (const Complex &o) const {
return {x + o.x, y + o.y};
}
Complex operator - (const Complex &o) const {
return {x - o.x, y - o.y};
}
Complex operator * (const Complex &o) const {
return {x * o.x - y * o.y, x * o.y + y * o.x};
}
} a[N], b[N], c[N];
int rev[N];
void fft(Complex a[], int Inv) {
for(int i = 0; i < tot; ++ i) {
if(i < rev[i]) {
swap(a[i], a[rev[i]]);
}
}
for(int mid = 1; mid < tot; mid <<= 1) {
auto w1 = Complex({cos(pi / mid), Inv * sin(pi / mid)});
for(int i = 0; i < tot; i += mid * 2) {
auto wk = Complex({1, 0});
for(int j = 0; j < mid; ++ j, wk = wk * w1) {
auto x = a[i + j], y = a[i + j + mid];
a[i + j] = x + wk * y;
a[i + j + mid] = x - wk * y;
}
}
}
if(Inv == -1) {
for(int i = 0; i < tot; ++ i) {
a[i].x /= tot;
}
}
}
string s, t;
int m, n, A[N], B[N];
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> m >> n >> s >> t;
reverse(s.begin(), s.end());
for(int i = 0; i < m; ++ i) {
A[i] = s[i] == '*' ? 0 : s[i] - 'a' + 1;
}
for(int i = 0; i < n; ++ i) {
B[i] = t[i] == '*' ? 0 : t[i] - 'a' + 1;
}
for(int i = 0; i < tot; ++ i) {
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << 18);
}
for(int i = 0; i < tot; ++ i) {
a[i] = Complex({A[i] * A[i] * A[i], 0});
b[i] = Complex({B[i], 0});
}
fft(a, 1), fft(b, 1);
for(int i = 0; i < tot; ++ i) {
c[i] = c[i] + a[i] * b[i];
}
for(int i = 0; i < tot; ++ i) {
a[i] = Complex({A[i], 0});
b[i] = Complex({B[i] * B[i] * B[i], 0});
}
fft(a, 1), fft(b, 1);
for(int i = 0; i < tot; ++ i) {
c[i] = c[i] + a[i] * b[i];
}
for(int i = 0; i < tot; ++ i) {
a[i] = Complex({A[i] * A[i], 0});
b[i] = Complex({B[i] * B[i], 0});
}
fft(a, 1), fft(b, 1);
for(int i = 0; i < tot; ++ i) {
c[i] = c[i] - Complex({2, 0}) * a[i] * b[i];
}
fft(c, -1);
vector<int> ans;
for(int i = m - 1; i < n; ++ i) {
ll v = c[i].x + 0.5;
if(v == 0) {
ans.push_back(i - m + 2);
}
}
cout << ans.size() << '\n';
for(int x : ans) cout << x << ' ';
return 0;
}
CF528D
题意:给定只含 ATGC 的两个字符串 \(s, \ t\) 和一个非负整数 \(k\),求有多少 \(i\) 满足任意 \(j \in [0, |t|)\),都存在 \(p \in [0, |s|)\) 使得 \(|i + j - p|\le k\) 且 \(s_p = t_j\)。
记 \(s\) 的长度为 \(n\),\(t\) 的长度为 \(m\)。
预处理第 \(i\) 个位置能否与字符 \(c\) 匹配,记做 \(b_{i, c}\)。
定义完全匹配函数 \(P(x)\),表示以 \(x\) 结尾的字符串与 \(t\) 匹配的个数,匹配成功当且仅当 \(P(x) = m\)。
\(P(x) = \sum\limits_{c\in t}\sum\limits_{t_i = c}b_{(x - m + i + 1, c)}\)。
单独考虑每个字符,记 \(f(x, A) = \sum_{i = 0}^{m - 1}[t_i = A][b_{x - m + i + 1, A}]\)。
按照套路将 \(t\) 翻转。
则 \(f(x, A) = \sum_{i = 0}^{m - 1}[t'_{m -i - 1} = A][b_{x - m + i + 1, A}]\)。
令 \(T(x) = \sum_{i \ge 0} [t'_i = A]x^i, \ B(x) = \sum_{i \ge 0}[b_{i, A}]x^i\),则 \(f(i, A) = [x^i]T(x)B(x)\)
拉格朗日插值
拉格朗日插值定理
\(n\) 个点值 \((x_i, y_i), \ (1\le i \le n)\),满足 \(x_i \neq x_j, \ (i\neq j)\),它们 唯一 确定一个 \(n - 1\) 次多项式 \(f(x)\) 满足
构造一个多项式 \(f(x) = f_1(x) + f_2(x) + \cdots + f_n(x)\)。
满足 \(f_i(x_j) = \begin{cases}y_j & i = j\\0 & i \neq j\end{cases}\)。
待定系数,\(f_1(x) = A(x - x_2)(x - x_3)\cdots(x - x_n)\)。
带入 \(x_1\),解出 \(A = \dfrac{y_1}{(x_1 - x_2)(x_1 - x_3)\cdots(x_1 - x_n)}\),其余 \(f_i\) 同理。
-
与 \(\text{CRT}\) 的关系?
多项式模多项式:如果 \(f(x) = q(x)g(x) + r(x)\),其中 \(r(x)\) 的次数小于 \(g(x)\),则记做 \(f(x)\equiv r(x)\pmod {g(x)}\)。
多项式互质:两个多项式的公因式只有常数,则称这两个多项式互质。
对于任意 \(i \in [1, n]\):
\[f(x) - f(x_i) =a_1(x - x_i) + a_2(x - x_i^2) + \cdots a_{n - 1}(x^{n - 1} - x_i^{n - 1}) \equiv 0 \pmod{x - x_i} \]有同余方程组
\[\begin{cases} f(x) \equiv f(x_1) \pmod {x - x_1}\\ \\ f(x) \equiv f(x_2) \pmod {x - x_2}\\ \\ \vdots\\ \\ f(x) \equiv f(x_{n - 1}) \pmod {x - x_{n - 1}}\\ \end{cases} \]显然有模数两两互质,满足中国剩余定理的使用条件。
-
暴力实现:先算 \(g(x) = \prod(x - x_i)\),再求 \(n\) 次 \(g(x) / (x - x_i)\),复杂度 \(O(n^2)\)。
-
特殊情况1:只要求一个 \(f(x_0)\),复杂度 \(O(n^2)\)。
-
特殊情况2:只要求一个 \(f(x_0)\),满足 \(x_i = i\),复杂度 \(O(n)\)(可以预处理)。
例题
CF622F
题意:求 \(\sum_{i = 1}^ni^k\pmod {10^9 + 7}, \ n \le 10^9, \ k \le 10^6\)。
\(f(n) = \sum_{i = 1}^ni^k\) 是关于 \(n\) 的 \(k + 1\) 次多项式。
证明:
对于第二类斯特林数,满足公式
那么
有组合恒等式
则
所以求出 \([0, k + 1]\) 的函数值,直接拉插即可。
Polynomia
题意:\(f(n)\) 是 \(n\) 次多项式,给定 \(f(i), \ i \in[0, n]\),询问 \(s(R) - s(L - 1)\)。
\(f(n)\) 是 \(n\) 次多项式,则其前缀和为 \(n + 1\) 次多项式。
先对 \(f(n)\) 做一遍拉插求出 \(f(n + 1)\),因而得到 \(s(n + 1)\),再对 \(s\) 做拉插。
reference
阶与原根
阶
若正整数 \(m, \ a\),满足 \((a, m) = 1\),则使 \(a^n\equiv 1 \pmod m\) 的最小正整数 \(n\) 称为 \(a\) 模 \(m\) 的阶,记作 \(\delta_m(a)\)。
\(\delta_7(1) = 1, \ \delta_7(2) = 3, \ \delta_7(3) = 6\)。
原根
若 \(\delta_m(a) = \varphi(m)\),则称 \(a\) 为 \(m\) 的一个原根。
欧拉定理:若 \((a, m) = 1\),则 \(a^{\varphi(m)}\equiv 1\pmod m\)。
阶的性质
假设 \((a, m) = 1, \ \delta = \delta_m(a)\),则
-
\(a^0, a^1, \dots, a^{\delta - 1}\) 在模 \(m\) 意义下两两不同。
证明:
如果存在 \(a^x \equiv a^y \pmod m, \ x < y \le \delta - 1\)。
则 \(a^{y - x} \equiv 1\),且 \(y - x < \delta\),与阶的最小性矛盾。
-
\(a^{\gamma}\equiv a^{\gamma'} \pmod m \iff \gamma \equiv \gamma'\pmod \delta\)。
-
\(\delta \mid \varphi(m)\)。
证明:
令 \(\varphi(m) = q\delta + r, \ (0 \le r < \delta)\)。
如果 \(r > 0\),则 \(a^{q\delta + r} \equiv a^{r} \equiv a^{\varphi(m)}\equiv 1 \pmod m\),则有 \(r < \delta\),与 \(\delta_m(a) = \delta\) 矛盾。
所以 \(r = 0\)。
-
设 \(m \in\mathbb{N^*}, \ a, b\in \mathbb{Z}, \ (a, m) = (b, m) = 1\),则
\[\delta_m(ab) = \delta_m(a)\delta_m(b) \]的充要条件为 \((\delta_m(a), \delta_m(b)) = 1\)。
-
设 \(k\in \mathbb{N}, \ m \in \mathbb{N^*}, \ a\in \mathbb{Z}, \ (a, m) = 1\),则
\[\delta_m(a^k) = \dfrac{\delta_m(a)}{(\delta_m(a), k)} \]证明:
注意到:
\[\begin{aligned} & a^{k\delta_m(a^k)}=(a^k)^{\delta_m(a^k)}\equiv 1 \pmod m \\ \implies & \delta_m(a)\mid k\delta_m(a^k) \\ \implies & \dfrac{\delta_m(a)}{\left(\delta_m(a),k\right)}\mid\delta_m(a^k) \end{aligned} \]另一方面,由 \(a^{\delta_m(a)}\equiv 1 \pmod m\),可知:
\[(a^k)^{\frac{\delta_m(a)}{(\delta_m(a),k)}}=(a^{\delta_m(a)})^{\frac{k}{(\delta_m(a),k)}}\equiv 1 \pmod m \]故:
\[\delta_m(a^k)\mid\dfrac{\delta_m(a)}{(\delta_m(a),k)} \]综合以上两点,得:
\[\delta_m(a^k)=\dfrac{\delta_m(a)}{(\delta_m(a),k)} \]
原根的存在与判定
原根的存在定理
只有模 \(2,\ 4,\ p^a,\ 2p^a\) (\(p\) 是奇质数)存在原根。
原根的判定定理
设 \(m > 1\),\(g\) 为正整数且 \((g, m) = 1\)。则 \(g\) 是 \(m\) 的原根当且仅当对于任意 \(\varphi(m)\) 的质因子 \(q_i\),\(g^{\varphi(m)/q_i} \not\equiv 1 \pmod m\)。
证明:如果 \(\delta < \varphi(m)\) 且 \(\delta \mid \varphi(m)\),则一定存在一个 \(q_i\) 使得 \(\delta \mid\varphi(m) / q_i\)。
原根个数
若 \(m\) 有原根,则它原根的个数为 \(\varphi(\varphi(m))\)。
证明:
若 \(m\) 有原根 \(g\),则:
所以若 \(\left(k,\varphi(m)\right)=1\),则有:\(\delta_m(g^k)=\varphi(m)\),即 \(g^k\) 也是模 \(m\) 的原根。
而满足 \(\left(\varphi(m),k\right)=1\) 且 \(1\leq k \leq \varphi(m)\) 的 \(k\) 有 \(\varphi(\varphi(m))\) 个。所以原根就有 \(\varphi(\varphi(m))\) 个。
指标(离散对数)
定义
对于质数 \(p\),假设 \(g\) 是 \(p\) 的一个原根,则 \(g^0, \ g^1, \dots, g^{p - 2}\) 在模 \(p\) 意义下是 \(1, 2, \dots, p - 1\) 的一个排列。
假设对于 \(x \in [1, p)\) 有 \(g^c\equiv x \pmod p\),则称 \(x\) 的指标为 \(c\),记作 \(\operatorname{ind}(x) = c\)(或 \(\operatorname{ind}_g(x) = c\))。
性质
对于任意 \(x, y \in [1, p)\),存在
类似于实数运算中的对数,因此指标亦称离散对数。
BSGS (baby step giant step)
给定质数 \(p\),求最小满足 \(g^c \equiv x \pmod {p}\) 的非负整数 \(c\) 的值。
令 \(c = aB + b\),其中 \(B = \lceil\sqrt{p}\rceil\)。
因为 \(c < \varphi(p) = p - 1\),所以 \(a, \ b < B\)。
-
BS:枚举 \(b = 0, \ 1, \ \dots, B - 1\),将 \(xg^{b}\) 计入哈希表。
-
GS:枚举 \(a = 1, \ 2, \ \dots, B\),若存在 \(g^{aB} = xg^b\),则最小满足条件的 \(c = aB - b\)。
这样枚举会漏掉 \(c = 0\) 的解,单独特判即可。
最小性证明:
对于 \(xg^b \bmod p\) 相同的 \(b\),大的会在哈希表中覆盖小的,从而使 \(aB - b\) 最小。
\(B > b\),所以 \(a\) 对答案的贡献大于 \(b\),从小到大枚举 \(a\) 使答案最小。
例题
Discrete Roots
题意:给出两个质数 \(p, k\) 和一个整数 \(a\),求 \(x^k = a \pmod p\) 的所有解。
所以只需处理 \(p\) 的原根以及 \(a\) 的指标,中间的同余方程可用 exgcd 求解。
特判 \(a = 0\) 的情况。
快速数论数论变换(NTT)
即把 FFT 中 \(\mathbb{C}\) 上的运算变成 \(\mathbb{Z}_p\) 上的运算。
-
假设素数 \(p\) 满足 \(p = r2^l + 1\),\(g\) 是 \(p\) 的原根。
-
用 \(g_n = g^{\frac{p - 1}{n}}\) 替代 \(\omega_n\)。
-
\(g_{2n}^{2k} \equiv g_n^k \pmod p, \ (2n < 2^l)\)。
-
\(g_{2n}^{n} \equiv -1 \pmod p, \ (2n < 2^l)\)。
\(g_{2n}^n = g^{\frac{p - 1}{2}}\)。
由于 \((g^{\frac{p - 1}{2}})^2 \equiv g^{p - 1} \equiv 1\pmod p\),所以 \(g_{2n}^n\) 只可能同余 \(1\) 或 \(-1\)。
又因为 \(g\) 为原根,\(\delta_{p}(g) = p - 1\)。
若 \(g^{\frac{p - 1}{2}} \equiv 1\) 则与阶的最小性矛盾,所以 \(g^{\frac{p - 1}{2}}\equiv-1\pmod p\)。
-
\(\sum_{k = 0}^{n - 1}g_{n}^{ik}g_{n}^{-kj} \equiv \begin{cases} n & i = j\\ 0 & i \neq j \end{cases}\pmod p\),其中 \(i, j \in [0, n)\)。
优点:快,精确。
限制:模数要满足 \(p = 2^l + 1\)。
常见模数:
-
\(65537 = 2^{16} + 1, \ g = 3\)。
-
\(998244353 = 119 \cdot 2^{23} + 1, \ g = 3\)。
-
\(1004535809 = 479 \cdot 2^{21} + 1, \ g = 3 \quad > 10^{9}\)。
-
\(4179340454199820289 = 29 \cdot 2^{57} + 1, \ g = 3 \quad> 4\cdot 10^{18}\)。
分治 FFT(NTT)
-
在模 \(998244353\) 意义下,计算 \(f(x) = \prod (x - a_i)\) 的各项系数。
-
计算 \([l, mid]\) 之积。
-
计算 \([mid + 1, r]\) 之积
-
\([l, mid]\) 与 \([mid + 1, r]\) 相乘。
时间复杂度 \(O(n\log^2n)\)。
-
-
在模 \(998244353\) 意义下,计算 \(f(x) = \prod f_i(x)\) 的各项系数,其中 \(\sum\deg(f_i(x)) \le 10^5\)。
可以和上题一样分治。
也可以按照次数维护一个优先队列,每次相乘当前最小的两个,即一棵哈夫曼树。
例题
P4721 【模板】分治 FFT
题意:给定 \(g_1 \dots g_{n - 1}\),求 \(f_0\dots f_{n - 1}\),满足 \(f_0 = 1\) 且 \(f_i = \sum_{j = 1}^ig_jf_{i - j}\)。
后式是一个卷积的形式,考虑分治。
假设当前正在处理区间 \([l, r]\)。
- 递归 \([l, mid]\),求出 \(f_l\dots f_{mid}\)。
- 计算 \(f_l\dots f_{mid}\) 对 \(f_{mid + 1}\dots f_r\) 的贡献。
- 递归 \([mid + 1, r]\)。
具体怎么求贡献?
令 \(\forall i \in [l, mid], \ a_{i - l} = f_l\)。
\(\forall i \in [1, r - l], \ b_{i - 1} = g_i\)。
对于 \(\forall i \in [mid + 1, r]\),加上 \([x^{i - l - 1}]A*B\) 的贡献。
void solve(int l, int r) {
if(l == r) {
return;
}
int mid = l + r >> 1;
solve(l, mid);
bit = 0;
while((1 << bit) < (r - l)) ++ bit;
tot = 1 << bit;
for(int i = 0; i < tot; ++ i) {
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << bit - 1);
}
memset(a, 0, tot * 8);
memset(b, 0, tot * 8);
for(int i = l; i <= mid; ++ i) a[i - l] = f[i];
for(int i = 1; i <= r - l; ++ i) b[i - 1] = g[i];
ntt(a, 1), ntt(b, 1);
for(int i = 0; i < tot; ++ i) a[i] = (ll)a[i] * b[i] % P;
ntt(a, -1);
for(int i = mid + 1; i <= r; ++ i) {
f[i] = (f[i] + a[i - l - 1]) % P;
}
solve(mid + 1, r);
}
C-挑选队友
题意:\(m\) 个群,\(n\) 位选手,选其中的k名,每个群中都应有至少一名,求方案数。
考虑生成函数 \(F_i(x) = \sum_{j = 1}^{s_i}\begin{pmatrix}s_i\\j\end{pmatrix}x^j\)。
则答案即 \([x^k]\prod F_i(x)\)。
实测分治时传 vector 的效率也不差。
D-tokitsukaze and Another Protoss and Zerg
和上题基本一致,生成函数略有不同。
如果星族选 \(0\) 个,则虫族可选任意一个非空子集。
所以 \(F_i(x) =(2^{b_i} - 1) + \sum_{j = 1}^{a_i}\begin{pmatrix}a_i\\j\end{pmatrix}x^j\)。
牛顿迭代
推导
给定多项式 \(g(x)\),求满足 \(g(f(x)) = 0\) 的形式幂级数 \(f(x)\)。
设 \(g(x) = b_0 + b_1x + \cdots b_kx^{k}, \ f(x) = a_0 + a_1x + \cdots\)。
设当前求出 \(f\) 的前 \(n\) 项。
-
\(n = 1\) 时,解 \(g(a_0) = 0\)。
-
假设已经求出前 \(n\) 项 \(f(x) \equiv a_0 + a_1x + \cdots a_{n - 1}x^{n - 1}\pmod {x^n}\)。
则 \(f(x) \equiv f_0(x) - \dfrac{g(f_0(x))}{g'(f_0(x))}\pmod{x^{2n}}\)。
证明:
对于 \(g(f(x))\),有泰勒展开
观察到 \(f(x) - f_0(x)\) 次数最小也有 \(x^n\)$。
所以在模 \(x^{2n}\) 意义下,从第三项开始都为 \(0\)。
根据定义 \(g(f(x)) = 0\)。
则 \(f(x) \equiv f_0(x) - \dfrac{g(f_0(x))}{g'(f_0(x))}\pmod{x^{2n}}\)。
多项式求逆
设 \(h(x)\) 是给定的形式幂级数,求它的逆 \(f(x)\),则 \(g(f(x)) = \dfrac{1}{f(x)} - h(x)\)。
得到的迭代式为(求导时 \(h(x)\) 可当做常数,\(f(x)\) 看成自变量)
边界 \([x^0]f(x) = [x^0]h^{-1}(x)\)。
时间复杂度 \(O(\sum\limits_{i = 1}^{\log N} i \cdot 2^i) = O(N\log N)\)。
介于本人不会求导,给出另一种推导方式。
已知 \(f_0(x) = f(x) \bmod {x^n}\)。
设 \(f_1(x) = f(x) \bmod x^{2n}\)。
有 \([f_1(x) - f_0(x)]^2 \equiv \pmod {x^{2n}}\)。
即
\[f_1^2(x) - 2f_1(x)f_0(x) + f_0^2(x) \equiv 0 \pmod{x^{2n}} \]在模 \(x^{2n}\) 意义下,\(f_1(x) * h(x) = 1\)。
两边同乘 \(h(x)\)。
\[f_1(x) - 2f_0(x) + f_0^2(x)h(x) \equiv 0 \pmod{x^{2n}} \]
void polyinv(ll *f, const ll *h, int n){
static ll d[N], g[N];
int V = 1; while(V < n + n - 1) V <<= 1;
memcpy(d, h, n * 8), memset(d + n, 0, (V - n) * 8);
memset(f, 0, V * 8), memset(g, 0, V * 8);
f[0] = qpow(h[0], P - 2);
for(int w = 2; w / 2 < n; w <<= 1){
memcpy(g, d, w * 8);
for(int i = 0; i < w * 2; ++i) rev[i] = (rev[i >> 1] >> 1) | (i & 1 ? w : 0);
ntt(f, w << 1, 1), ntt(g, w << 1, 1);
for(int i = 0; i < w * 2; ++i) f[i] = (2 - f[i] * g[i]) % P * f[i] % P;
ntt(f, w << 1, -1);
memset(f + w, 0, w * 8);
}
memset(f + n, 0, (V - n) * 8);
}
-
\(n\) 为项数而不是次数。
-
\(w\) 是 \(f_1(x)\) 的长度,当前已知长度为 \(w / 2\) 的 \(f_0(x)\)。
-
由于要算 \(f_0^2(x) * h(x)\),所以 ntt 要开到 \(4\) 倍 \(w / 2\)。
-
做完 idft 后只需保留前 \(w\) 项,否则后续有影响。
多项式开方
设 \(h(x)\) 是给定的形式幂级数,求它的开方 \(f(x)\),则 \(g(f(x)) = f(x)^2 - h(x)\)。
得到的迭代式为:
void polysqrt(ll *f, const ll *h, int n){
static ll d[N], g[N], f_inv[N];
int V = 1; while(V < n + n - 1) V <<= 1;
memcpy(d, h, n * 8), memset(d + n, 0, (V - n) * 8);
memset(f, 0, V * 8), memset(g, 0, V * 8), memset(f_inv, 0, V * 8);
f[0] = 1;
constexpr int i2 = 499122177;
for(int w = 2; w / 2 < n; w <<= 1){
memcpy(g, d, w * 8);
for(int i = 0; i < w * 2; ++i) rev[i] = (rev[i >> 1] >> 1) | (i & 1 ? w : 0);
polyinv(f_inv, f, w);
ntt(f, w << 1, 1), ntt(g, w << 1, 1), ntt(f_inv, w << 1, 1);
for(int i = 0; i < w * 2; ++i) f[i] = (f[i] + f_inv[i] * g[i]) % P * i2 % P;
ntt(f, w << 1, -1);
memset(f + w, 0, w * 8);
}
memset(f + n, 0, (V - n) * 8);
}
例题
CF438E The Child and Binary Tree
题意:给定集合 \(\{c_1, c_2, \dots, c_n\}\quad(c_i \ge 1)\),有根二叉树的点权都属于该集合,左右儿子区分,问满足点权和 \(s = 1, 1, \dots,m\) 有多少不同二叉树。
令 \(f_n\) 表示点权和为 \(n\) 时的方案数。
令 \(v_i\) 表示 \(i\) 这个点权是否在集合中出现。
枚举左右子树的权值
下式可写成卷积的形式:
令 \(F(x) = \sum_{i \ge 1} f_0x^{i}\)。
\(G(x) = \sum_{i \ge 1}[v_i]x^{i}\)。
那么
由于题目保证了 \(c_i > 0\),所以 \([x^0]G(x) = 0\)。
则 \(F = F^2G + 1\)。
解方程:
-
\(\lim\limits_{x\rightarrow 0}F(x) = f_0 = 1\)。
-
\(\lim\limits_{x\rightarrow 0}G(x) = 0\)。
取正号时,有 \(\lim\limits_{x\rightarrow 0}F(x) = +\infty\),舍去。
取负号时,有 \(\lim\limits_{x\rightarrow 0}F(x) = 1\),成立。
所以
\([x^0]G(x) = 0\),无法求逆,考虑上下同乘 \(1 + \sqrt{1 - 4G}\)。
得
法2:牛顿迭代。
\(g(F(x)) = G(x)F^2(x) - F(x) + 1 = 0\)。
-
\(F(x) \equiv 1 \pmod {x}\)。
-
\(F(x) \equiv F_0(x)- \dfrac{G(x)F_0^2(x) + 1}{2G(x)F_0(x) - 1} \pmod {x^{2n}}\)。
F-卷积
题意:定义 \(F(x)=\sum_{i=1} f_ix^i\) ,其中 \(f_i=af_{i-1}+bf_{i-2}|(i>=2),f_0=0,f_1=1\) 。
给定 \(n, a, b\),求 \([x^{n}]\sum_{i\ge 1}F^i(x)\),(\(n \le 2\times 10^6\))。
则 \(F(x) = \dfrac{1}{1 - ax - bx^2}\)。
\(\sum_{i\ge1}F^i(x) = \dfrac{F(x)}{1 - F(x)} = \dfrac{x}{1 -(a + 1)x - bx^2}\)。
令 \(G(x) = \dfrac{1}{1 -(a + 1)x - bx^2}\),则答案转化为求 \([x^{n -1}]G(x)\)。
到此步为止,已经可以 \(O(n\log n)\) 多项式求逆了。
复杂度依旧吃紧。
继续观察。
将 \(G(x)\) 与 \(F(x)\) 比对,形式出奇一致。
得到 \(g_i = (a + 1)g_{i - 1} + bg_{i - 2}\),求 \(g_{n - 1}\)。
可以 \(O(n)\) 计算,也可以 \(O(4\log N)\) 矩阵快速幂。
形式幂级数的更多运算
形式幂级数与幂级数的比较
- 形式幂级数本质是序列(\(x^i\) 无意义),幂级数本质是极限。
- 形式幂级数通过带入 \(x\) 还原成幂级数。
- 假设系数在 \(\mathbb{C}\) 上,可以证明形式幂级数与具有正收敛半径的幂级数在 '通常' 的所有运算上服从同样规律(加减乘除求导积分……)。
形式幂级数的更多运算
假设 \(f(x) = a_0 + a_1x + a_2x^2 + \cdots + a_nx^{n} + \cdots\)。
求导
定义 \(f(x)\) 的导数为 \(a_1 + 2a_2x + \cdots + (n + 1)a_{n + 1}x^{n} + \cdots\),记做 \(f'(x)\) 或 \(\dfrac{df(x)}{d(x)}\)。
对于形式幂级数而言,
求导是序列上的一个变换,即 \(\{a_0, a_1, \cdots, a_n,\cdots\} \Rightarrow \{a_1, 2a_2, \cdots, (n + 1)a_{n + 1},\cdots\}\)
积分
定义 \(f(x)\) 的积分为 \(a_0x + \dfrac{a_1}{2}x^2 + \cdots + \dfrac{a_{n - 1}}{n}x^{n} + \cdots\),记做 \(\int f(x)dx\) 或 \(\int_{0}^{x} f(y)dy\)。
即 \(\{a_0, a_1, \cdots, a_n,\cdots\} \Rightarrow \{0, a_0, \dfrac{a_1}{2}, \cdots, \dfrac{a_{n - 1}}{n},\cdots\}\)。
推论:如果 \([x^0]f(x) = 0\),令 \(g(x) = f'(x)\),则 \(\int g(x)dx = f(x)\)。
复合
假设 \(f(x) = a_1x + a_2x^2 + \cdots + a_nx^{n} + \cdots, \ g(x) = b_0 + b_1x + b_2x^2 + \cdots + b_nx^{n} + \cdots\)。
则 \(g\) 复合 \(f\) 定义为 \(c_0 + c_1x + \cdots c_nx^n + \cdots\),满足 \(c_0 = b_0, \ c_n = \sum\limits_{k = 1}^{n}b_k\sum\limits_{i_1 + i_2 + \cdots+ i_k = n}\prod a_{i_j}\)。
记做 \(g \circ f\) 或 \(g(f(x))\)。
如果 \(f\) 的常数项不为 \(0\)。
那么 \(c_0 = b_0 + b_0a_0 + b_0a_0^2 + \cdots + b_na_0^n + \cdots\)。
则 \(c_0\) 本身就是一个极限的形式,涉及到收不收敛的问题,这是在形式幂级数中不愿看到的。
因此在定义复合时,一般令 \([x^0]f(x) = 0\)。
再考虑 \(c_n = \sum\limits_{k = 1}^{n}b_k\sum\limits_{i_1 + i_2 + \cdots+ i_k = n}\prod a_{i_j}\)。
如果 \(i_j > n\),那么 \(\sum{i_j} > n\),所以 \(c_n\) 的定义不需要考虑收敛。
- \(\exp(x) = \sum_{n \ge0} \dfrac{1}{n!}x^n\)。
- \(\ln (1 + x) = \sum_{n \ge 1}(-1)^{n + 1}\dfrac{x^n}{n}\)。
- \(\ln (1 - x) = -\sum_{n \ge 1}\dfrac{x^n}{n}\)。
- 设形式幂级数 \(f(x)\) 满足 \([x^0]f(x) = 0\),则可定义 \(\exp(f(x))\) 和 \(\ln(1 + (f(x))\)。(或 \([x^0] = 1\) 可定义 \(\ln(f(x))\))。
- \(g(x) = \exp(f(x)) \iff f(x) = \ln(g(x))\)。
推论:\((g \circ f)' = (g' \circ f) \cdot f'\)。
假设 \(f(x) = \sum_{i \ge 1} a_ix^i, \ g(x) = \sum_{i \ge0}b_i, \ g(f(x)) = \sum_{i \ge0}c_ix^i\)。
满足
即证 \((n + 1)c_{n + 1} = \sum\limits_{i = 0}^{n}(i + 1)a_{i + 1}{}d_{n - i}\)。
左边:
右边:
左边等于右边。
计算 \(\ln(f(x))\)
(满足 \([x^0]f(x) = 1\))重要观察:
\(O(n)\) 求导,\(O(n\log n)\) 求逆,\(O(n)\) 积分。
计算 \(\exp(f(x))\)
(满足 \([x^0]f(x) = 1\))如果 \(g(x) = \exp(f(x))\),那么 \(\ln(g(x)) =f(x)\)。
构造牛顿迭代 \(h(g(x)) = \ln(g(x)) - f(x)\)。
有递推式
例题
三轮
题意:\(n\) 种商品,每种商品体积为 \(v_i\),都有 \(10^5\) 件,输出凑成 \(1\) 到 \(m\) 的体积的总方案数。
对质数 \(19260817\) 取模 。(\(n, m, v_i \le 5\times 10^4\))
\(v_i\) 至少为 \(1\),可认为每种商品都有无穷件。
考虑其生成函数 \(F_i(x) = 1 + x^{v_i} + x^{2v_i} + \cdots = \dfrac{1}{1 - x^{v_i}}\)。
所以 \(G(x) = \prod\limits_{i = 1}^{k} \dfrac{1}{1 - x^{v_i}}\) 。
由于 \(v_i\) 很大,无法分治 ntt 求解。
将积化为和,两边取对数。
第二类斯特林数
第二类斯特林数(斯特林子集数)\(\begin{Bmatrix}n\\ k\end{Bmatrix}\),也可记做 \(S_2(n,k)\),表示将 \(n\) 个两两不同的元素,划分为 \(k\) 个互不区分的非空子集的方案数。
递推关系
我们插入一个新元素时,有两种方案:
- 将新元素放入一个现有的非空子集,有 \(k\begin{Bmatrix}n-1\\ k\end{Bmatrix}\) 种方案。
- 将新元素单独放入一个子集,有 \(\begin{Bmatrix}n-1\\ k-1\end{Bmatrix}\) 种方案;
边界是 \(\begin{Bmatrix}n\\ 0\end{Bmatrix}=[n=0]\)。
通项公式
不妨先认为 \(k\) 个集合互不相同,转化成经典容斥问题,最后乘上 \(\dfrac{1}{k!}\)。
则
重要公式
记下降阶乘幂 \(x^{\underline{n}}=\dfrac{x!}{(x-n)!}=\prod_{k=0}^{n-1} (x-k)\)。
则可以利用下面的恒等式将普通幂转化为下降幂:
考虑各式组合意义。
- \(x^n \rightarrow\) \(n\) 个不同的球放入 \(x\) 个不同的盒子。
- \(\begin{pmatrix}x\\ k\end{pmatrix} \rightarrow\) \(x\) 个盒子中选出 \(k\) 个。
- \(\begin{Bmatrix}n\\ k\end{Bmatrix} \rightarrow\) \(n\) 个不同的球放入 \(k\) 个相同的盒子且都不为空。
- \(k! \rightarrow\) 将选出的 \(k\) 个盒子排列。
正确性显然。
指数生成函数
不妨将盒子染成 \(k\) 种不同颜色,每种颜色在长度为 \(n\) 的排列中必须出现一次。
对于第一种颜色,\(F_1(x) = x + \dfrac{x^2}{2!} + \dfrac{x^3}{3!} + \cdots = \exp(x) - 1\)(没有零次项,因为必须出现)。
全部的合法方案为 \([x^n]\prod F_i\)。
最后将染色去除,得到 \(G(x) = \dfrac{1}{k!}(\exp(x) - 1)^k\)。
第二类斯特林数·列
利用公式
其中
如果 \([x^0]f(x) \neq 1\) 则不能直接求对。
考虑给每项除以一个公因式 \(a_ix^i\),满足第 \(i\) 项是系数非 \(0\) 的最低项。
最后再乘上 \((a_ix^i)^k\)。
EGF 求得的系数为 \(\dfrac{a_n}{n!}\)。
第二类斯特林数·行
令 \(F(x) = \sum_{i \ge 0} \dfrac{(-1)^i}{i!}x^i \,, \ G(x) = \sum_{i \ge 0} \dfrac{i^n}{i!}x^i\)。
于是 \(S_2(n) = F * G\)。
第一类斯特林数
有 \(k\) 个轮换的 \(n\) 元置换的方案,记为 \(c(n, k)\) 或 \(\begin{bmatrix}n\\k\end{bmatrix}\)。
置换向原位置连边,形成若干个环,即轮换。
对于置换 \(\sigma = \begin{pmatrix}1 & 2 & 3 & 4 & 5\\3 & 5 & 1 & 2 & 4\end{pmatrix}\),有两个轮换:
递推关系
边界:\(\begin{bmatrix}0\\0\end{bmatrix} = \begin{bmatrix}1\\1\end{bmatrix} = 1\)。
-
自己向自己连边,单独成环。
-
已经有了 \(k\) 个环,在 \(n - 1\) 个空隙里选一个插入。
重要公式
上升幂转普通幂
假设 \(x^{\overline{n}} = \sum\limits_{k = 0}^nf(n, k)x^k\)。
联立
得到 \(f\) 的递推式:\(f(n, k) = f(n - 1, k - 1) + (n - 1)\cdot f(n - 1, k)\)。
发现 \(f\) 与第一类斯特林数递推式相同,初值相同,证毕。
下降幂转普通幂
用 \(-x\) 带入 \(1\) 中的 \(x\):
把左式的负号移至右式,即证。
指数生成函数
等效于 \(n\) 个不同球放入 \(k\) 个互不区分且非空的盒子,装有 \(i\) 个球的盒子有 \((i - 1)!\) 种不同形态,求方案数。
\(i\) 个球只用大小为 \(i\) 的盒子的方案为 \((i - 1)!\)。
先将盒子编号,对于每个盒子,有生成函数 \(F(x) = x + \dfrac{x^2}{2!} + 2!\cdot\dfrac{x^3}{3!} + \cdots = -\ln(1 - x)\)。
有 \(k\) 个盒子,则 \(G(x) = \dfrac{1}{k!}[-\ln(1 - x)]^k\)。
第一类斯特林数·列
第一类斯特林数·行
展开
显然可以分治 ntt \(O(n\log^2n)\) 求(但被出题人卡了)。
考虑倍增。
令 \(f(x) = \prod\limits_{i = 0}^{n - 1}(x + i) = \sum\limits_{i = 0}^{n}a_ix^i\),则 \((x + n)^\overline{n} = f(x + n)\)。
问题转化为已知多项式 \(f(x)\),快速求 \(f(x + c)\)。
第二个求和式可以写成 \(g(x) = \sum i!\cdot a_ix^{i}, \ h(x) = \sum \dfrac{c^i}{i!}x^{n - i}\) 的卷积。
则 \([x^j]f(x + c) = [x^{j + n}]g*h\)。
时间复杂度 \(T(n) = T(n / 2) + O(n\log n) = O(n\log n)\)。
有符号的第一类斯特林数
定义:\(S_1(n, k) = (-1)^{n + k}\begin{bmatrix}n\\k\end{bmatrix}\)。
重要公式
指数生成函数
两类斯特林数的关系及斯特林反演
证明:
对于公式 \(x^{n} = \sum\limits_{k = 0}^n\begin{Bmatrix}n\\k\end{Bmatrix}x^\underline{k}\),可以写成向量之积:
对于 有符号 第一类斯特林数:
我们有 \(S_1\times S_2 = I\)。
则在 \(S_1\) 中取一行 \(n\),在 \(S_2\) 中取一列 \(m\),两个向量之积为 \(1\) 当且仅当 \(m = n\)。
即 \(\sum_{k \ge 0} (-1)^{n + k}\begin{bmatrix}n\\k\end{bmatrix}\begin{Bmatrix}k\\m\end{Bmatrix} = [n = m]\)。
斯特林反演
证明:
整数拆分
\(n\) 的 \(k\) 无序拆分
\(n\) 个无标号球分配到 \(k\) 个无标号盒子的方案数,满足每个盒子不为空,记为 \(p(n, k)\)。
递推关系
假设第 \(i\) 个盒子(第 \(i\) 行)里有 \(a_i\) 个球,满足 \(a_1 \ge a_2\cdots\ge a_k \ge 1\)。
分两部分考虑。
- 第 \(k\) 个盒子有且仅有新加入的一个球,方案为 \(p(n - 1, k - 1)\)。
- 第 \(k\) 个盒子不止一个球,把黄色一列去掉,方案为 \(p(n - k, k)\)。
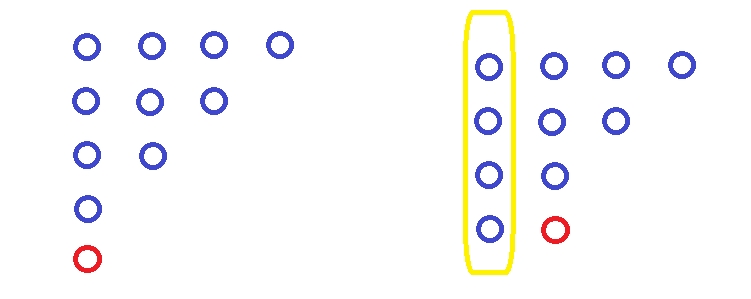
常生成函数
考虑上图中有多少有 \(i\) 个球的列。
\(i\) 个球时,只能有 \(1\) 列,一种方案。
\(2i\) 个球时,只能有 \(2\) 列,一种方案。
因此其常生成函数为 \(F_i(x) = 1 + x^{i} + x^{2i} + \cdots = \dfrac{1}{1 - x^i}\)。
记 \(G_k = \prod_{i = 1}^kF_i\)。
由于至少要有一列为 \(k\),所以
- 快速求 \(P_k\) 的前 \(n\) 项:对后式先取 \(\ln\) 再 \(\exp\),详见 形式幂级数的更多运算-例题-三轮。\[\sum\limits_{i = 1}^{k} \ln\dfrac{1}{1 - x^{i}} = \sum\limits_{i = 1}^{k} \sum_{j \ge 1} \dfrac{x^{ij}}{j} \]
\(n\) 的无序拆分
\(n\) 个无标号球分配到一些无标号盒子的方案数,满足每个盒子不为空,记为 \(p(n)\)。
可知 \(p(n) = \sum_{k = 1}^np(n, k)\)。
常生成函数
延续上板的思考方向,行的个数没有限制,所以只要一些长度为 \(i\) 的凑出 \(n\) 个球即可。
那么
递推关系
证明繁琐,当结论记。
产生贡献的项只有 \(O(\sqrt N)\) 个,复杂度 \(O(N\sqrt N)\)。
主要运用于模数不友好的情况。
生成函数模型
分配问题总结
\(n\) 个球放入 \(k\) 个盒子,球方案数。
p(n + k, k):把每行之前都加一个球,则 \(k\) 个盒子都不为空
分配问题(加强版1)
把 \(n\) 个球放入 \(k\) 个盒子,装有 \(i\) 个球的盒子有 \(f_i\) 种形态,不同形态算不同方案,有多少种方案?
设 \(\{f_i\}_{i\ge1}\) 的常生成函数 \(F(x) = \sum_{i\ge1}f_ix^i\),其指数生成函数 \(E(x) = \sum_{i \ge 1}\dfrac{f_i}{i!}x^i\)(有没有常数项取决于需不需要每个盒子都有球)。
则
分配问题(加强版2)
把 \(n\) 个球放入一些盒子且每个盒子都不为空,装有 \(i\) 个球的盒子有 \(f_i\) 种形态,不同形态算不同方案,有多少种方案?
设 \(\{f_i\}_{i\ge1}\) 的常生成函数 \(F(x) = \sum_{i\ge1}f_ix^i\),其指数生成函数 \(E(x) = \sum_{i \ge 1}\dfrac{f_i}{i!}x^i\)。
即对加强版 \(1\) 做个 \(\sum_{i\ge0}\)。
无标号/无标号:
考虑大小为 \(i\) 的盒子的常生成函数(即 \([x^n]\) 表示只用大小为 \(i\) 的盒子放入 \(n\) 个球的方案)。
对于盒子的第一种形态 \(g(x) = 1 + x^i + x^{2i} + \cdots\)。
以此类推,其常生成函数为 \(g^{f_i - 1}(x)\)。
所以无标号/无标号的常生成函数为
例题
CF961G Partitions
题意:
给出 \(n\) 个物品,每个物品有一个权值 \(w_i\)。
定义一个集合 \(S\) 的权值 \(W(S)=|S|\sum\limits_{x\in S}w_x\)。
定义一个划分的权值为 \(W'(R)=\sum\limits_{S\in R}W(S)\)。
求将 \(n\) 个物品划分成 \(k\) 个集合的所有方案的权值和。答案对 \(10^9+7\) 取模。
\(n,k\le2\times10^5\),\(w_i\le10^9\)。
感性理解,每个数的贡献是相同的,所以答案一定是 \(P\cdot \sum a_i\) 的形式。
枚举当前元素所在集合大小。
单独计算后面一个求和式,把 \(k - j - 1\) 当作常数 \(t\)。
则
时间复杂度 \(O(n\log n)\)。
还有一种更为精巧的解法:
考虑 \(w_i\) 会对答案产生多少次贡献?
在一个大小为 \(|S|\) 的集合中,\(w_i\) 贡献 \(|S|\) 次,等效于集合中每一个元素都使 \(w_i\) 产生一次贡献。
分两部分讨论
-
自己使自己的产生的贡献,显然每一种划分产生一次,共 \(\begin{Bmatrix}n\\k\end{Bmatrix}\) 次。
-
其他元素使自己的产生的贡献,把其余 \(n - 1\) 个球划分好 \(k\) 个集合,对于每种划分,当前元素可以任选一个集合放进去,因此 \(n - 1\) 个物品都会有一次贡献,共 \((n - 1)\begin{Bmatrix}n - 1\\k\end{Bmatrix}\)。
综上 \(P = \begin{Bmatrix}n\\k\end{Bmatrix} + (n - 1)\begin{Bmatrix}n-1\\k\end{Bmatrix}\)。
CF960G Bandit Blues
题意:给定 \(n, \ a, \ b\),定义 \(A\) 为一个排列中是前缀最大值的数的个数,定义 \(B\) 为一个排列中是后缀最大值的数的个数,求长度为 \(n\) 的排列中满足 \(A = a\) 且 \(B = b\) 的排列个数。\(n \le 10^5\),对 \(998244353\) 取模。
首先,排列里最大值一定同时是前缀最大和后缀最大,如果存在 \(a/b = 0\),无解。
令 \(f(i, j)\) 表示 \(i\) 个数的排列有 \(j\) 个前缀最大的方案。
不妨从大到小一个一个填。
- 填到序列的最前面,一定是前缀最大,有 \(f(i - 1, j - 1)\) 种情况。
- 由于所有数都比他大,填到任意一个数后面,有 \((i - 1)f(i - 1, j)\) 种情况。
所以 \(f(i, j) = f(i - 1, j - 1) + (n - 1) f(i - 1, j)\),恰为第一类斯特林数的递推式,由于边界相同,所以 \(f(i, j) = \begin{bmatrix}i\\j\end{bmatrix}\)。
枚举最大值左边的元素个数。
则答案为 \(\sum\limits_{i = 0}^{n - 1}\begin{pmatrix}n - 1\\i\end{pmatrix}\begin{bmatrix}i\\a - 1\end{bmatrix}\begin{bmatrix}n - i - 1\\b - 1\end{bmatrix}\)。
可以直接求出两列斯特林数,但形式仍不够优美。
考虑式子的组合意义:选出 \(i\) 个排成 \(a - 1\) 个环 \(\rightarrow\) 剩下 \(n - 1 - i\) 个排成 \(b - 1\) 个环。
也就是 \(n - 1\) 个元素排成 \(a + b - 2\) 个环,选其中 \(a - 1\) 个分给左边。
于是答案化简为 \(\begin{bmatrix}n - 1\\a + b- 2\end{bmatrix}\begin{pmatrix}a + b - 2\\a - 1 \end{pmatrix}\)。
第一列斯特林数没有实用的通项公式,随便求出一行或一列即可。
附录:模板
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
constexpr int N = 5e5 + 5, P = 998244353; // g = 3
ll gg[30], ig[30], fac[N], ifac[N], inv[N];
ll qpow(ll a, ll b) {
ll ret = 1;
while(b) {
if(b & 1) ret = ret * a % P;
b >>= 1;
a = a * a % P;
}
return ret;
}
void init() {
gg[0] = ig[0] = 1;
for(int i = 1; i < 30; ++ i) gg[i] = qpow(3, (P - 1) / (1 << i));
for(int i = 1; i < 30; ++ i) ig[i] = qpow(gg[i], P - 2);
fac[0] = 1;
for(int i = 1; i < N; ++ i) {
inv[i] = (i == 1) ? 1 : -(P / i) * inv[P % i] % P;
fac[i] = fac[i - 1] * i % P;
}
ifac[N - 1] = qpow(fac[N - 1], P - 2);
for(int i = N - 1; i >= 1; -- i) {
ifac[i - 1] = ifac[i] * i % P;
}
}
int rev[N];
void ntt(ll *a, int tot, int ty) {
for(int i = 0; i < tot; ++ i) {
if(i < rev[i]) {
swap(a[i], a[rev[i]]);
}
}
int t = 1;
for(int mid = 1; mid < tot; mid <<= 1, ++ t) {
ll g1 = gg[t];
if(ty == -1) {
g1 = ig[t];
}
for(int i = 0; i < tot; i += mid * 2) {
ll gk = 1;
for(int j = 0; j < mid; ++ j, gk = gk * g1 % P) {
ll x = a[i + j], y = a[i + j + mid];
a[i + j] = (x + gk * y) % P;
a[i + j + mid] = (x - gk * y) % P;
}
}
}
if(ty == -1) {
ll tmp = qpow(tot, P - 2);
for(int i = 0; i < tot; ++ i) {
a[i] = a[i] * tmp % P;
}
}
}
void polymul(ll *f, const ll *g, const ll *h, int n, int m) { // 项数,非次数
static ll a[N], b[N];
int tot = 1, bit = 0;
while(tot < n + m - 1) ++ bit, tot <<= 1;
for(int i = 0; i < tot; ++ i) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << bit - 1);
memcpy(a, g, n * 8), memset(a + n, 0, (tot - n) * 8);
memcpy(b, h, m * 8), memset(b + m, 0, (tot - m) * 8);
ntt(a, tot, 1), ntt(b, tot, 1);
for(int i = 0; i < tot; ++ i) a[i] = a[i] * b[i] % P;
ntt(a, tot, -1);
memcpy(f, a, tot * 8);
}
void polyinv(ll *f, const ll *h, int n){
static ll d[N], g[N];
int V = 1; while(V < n + n - 1) V <<= 1;
memcpy(d, h, n * 8), memset(d + n, 0, (V - n) * 8);
memset(f, 0, V * 8), memset(g, 0, V * 8);
f[0] = qpow(h[0], P - 2);
for(int w = 2; w / 2 < n; w <<= 1){
memcpy(g, d, w * 8);
for(int i = 0; i < w * 2; ++i) rev[i] = (rev[i >> 1] >> 1) | (i & 1 ? w : 0);
ntt(f, w << 1, 1), ntt(g, w << 1, 1);
for(int i = 0; i < w * 2; ++i) f[i] = (2 - f[i] * g[i]) % P * f[i] % P;
ntt(f, w << 1, -1);
memset(f + w, 0, w * 8);
}
memset(f + n, 0, (V - n) * 8);
}
void polysqrt(ll *f, const ll *h, int n){
static ll d[N], g[N], f_inv[N];
int V = 1; while(V < n + n - 1) V <<= 1;
memcpy(d, h, n * 8), memset(d + n, 0, (V - n) * 8);
memset(f, 0, V * 8), memset(g, 0, V * 8), memset(f_inv, 0, V * 8);
f[0] = 1;
constexpr int i2 = 499122177;
for(int w = 2; w / 2 < n; w <<= 1){
memcpy(g, d, w * 8);
for(int i = 0; i < w * 2; ++i) rev[i] = (rev[i >> 1] >> 1) | (i & 1 ? w : 0);
polyinv(f_inv, f, w);
ntt(f, w << 1, 1), ntt(g, w << 1, 1), ntt(f_inv, w << 1, 1);
for(int i = 0; i < w * 2; ++i) f[i] = (f[i] + f_inv[i] * g[i]) % P * i2 % P;
ntt(f, w << 1, -1);
memset(f + w, 0, w * 8);
}
memset(f + n, 0, (V - n) * 8);
}
void polyder(ll *f, const ll *h, int n) { // 项数,非次数
for(int i = 0; i <= n - 1; ++ i) {
f[i] = (i + 1) * h[i + 1] % P;
}
f[n - 1] = 0;
}
void polyint(ll *f, const ll *h, int n) { // 项数,非次数
for(int i = n - 1; i >= 1; -- i) {
f[i] = h[i - 1] * inv[i] % P;
}
f[0] = 0;
}
void polyln(ll *f, const ll *h, int n) { // h[0] = 1
static ll a[N], b[N];
polyinv(a, h, n);
polyder(b, h, n);
polymul(a, a, b, n, n);
polyint(f, a, n);
}
void polyexp(ll *f, const ll *h, int n) { // h[0] = 0
static ll d[N], g[N], f_ln[N];
int V = 1; while(V < n + n - 1) V <<= 1;
memcpy(d, h, n * 8), memset(d + n, 0, (V - n) * 8);
memset(f, 0, V * 8), memset(g, 0, V * 8), memset(f_ln, 0, V * 8);
f[0] = 1; //ln(h[0])
for(int w = 2; w / 2 < n; w <<= 1){
memcpy(g, d, w * 8);
for(int i = 0; i < w * 2; ++i) rev[i] = (rev[i >> 1] >> 1) | (i & 1 ? w : 0);
polyln(f_ln, f, w);
ntt(f, w << 1, 1), ntt(g, w << 1, 1), ntt(f_ln, w << 1, 1);
for(int i = 0; i < w * 2; ++i) f[i] = (1 - f_ln[i] + g[i]) % P * f[i] % P;
ntt(f, w << 1, -1);
memset(f + w, 0, w * 8);
}
memset(f + n, 0, (V - n) * 8);
}
void polypow(ll *f, ll *h, string K, int n) {
int cur = 0;
while(cur < n && h[cur] == 0) ++ cur;
ll k1 = 0, k2 = 0;
for(auto ch : K) {
if((k1 * 10 + ch - '0') * cur >= n || cur == n) {
for(int i = 0; i < n; ++ i) f[i] = 0;
return;
}
k1 = (k1 * 10 + ch - '0') % P;
k2 = (k2 * 10 + ch - '0') % (P - 1);
}
ll h_cur = h[cur], icur = qpow(h_cur, P - 2);
for(int i = cur; i < n; ++ i) {
f[i - cur] = h[i] * icur % P;
}
polyln(f, f, n - cur);
for(int i = 0; i < n - cur; ++ i) f[i] = f[i] * k1 % P;
polyexp(f, f, n - cur);
h_cur = qpow(h_cur, k2);
for(int i = n - 1; i >= k1 * cur; -- i) f[i] = f[i - k1 * cur] * h_cur % P;
for(int i = 0; i < k1 * cur; ++ i) f[i] = 0;
}
void Stirling2ndCol(ll *f, int n, int k) { //S2(0...n, k)
for(int i = 1; i <= n; ++ i) {
f[i] = ifac[i];
}
polypow(f, f, to_string(k), n + 1);
for(int i = 0; i <= n; ++ i) {
f[i] = f[i] * ifac[k] % P * fac[i] % P;
}
}
void Stirling2ndRow(ll *f, int n) { // S2(n, 0...n)
static ll g[N];
for(int i = 0; i <= n; ++ i) {
f[i] = (i & 1) ? -ifac[i] : ifac[i];
g[i] = qpow(i, n) * ifac[i] % P;
}
polymul(f, f, g, n + 1, n + 1);
}
void Stirling1stCol(ll *f, int n, int k) { //c(0...n, k)
for(int i = 2; i <= n; ++ i) {
f[i] = 0;
}
f[0] = 1, f[1] = -1;
polyln(f, f, n + 1);
for(int i = 0; i <= n; ++ i) f[i] = -f[i];
polypow(f, f, to_string(k), n + 1);
for(int i = 0; i <= n; ++ i) {
f[i] = f[i] * ifac[k] % P * fac[i] % P;
}
}
void Offset(ll *f, ll *h, int n, int c) { // f <-- h(x + c) 偏移 n次多项式
static ll g[N], d[N];
for(int i = 0; i <= n; ++ i) {
g[i] = fac[i] * h[i] % P;
d[i] = (i == 0 ? 1 : d[i - 1] * c % P);
}
for(int i = 0; i <= n; ++ i) d[i] = d[i] * ifac[i] % P;
reverse(d, d + n + 1);
polymul(f, g, d, n + 1, n + 1);
for(int i = 0; i <= n; ++ i) {
f[i] = f[i + n] * ifac[i] % P;
}
memset(f + n + 1, 0, n);
}
void Stirling1stRow(ll *f, int n) { // c(n, 0...n)
static int stk[30], tp;
static ll g[N];
tp = 0;
while(n) {
stk[++ tp] = n;
n >>= 1;
}
f[0] = 0, f[1] = 1;
n = 1;
while(-- tp) {
Offset(g, f, n, n);
polymul(f, f, g, n + 1, n + 1);
n <<= 1;
if(stk[tp] == n + 1) {
f[n + 1] = f[n];
for(int i = n; i >= 1; -- i) {
f[i] = (f[i] * n + f[i - 1]) % P;
}
++ n;
}
}
}
void Partition(ll *f, int n) {
memset(f, 0, (n + 1) * 8);
for(int i = 1; i <= n; ++ i) {
for(int j = i; j <= n; j += i) {
f[j] = (f[j] + inv[i]) % P;
}
}
polyexp(f, f, n + 1);
}
ll n, k, f[N];
int main() {
cin.tie(0)->sync_with_stdio(0);
init();
return 0;
}
Reference
《线性代数》(机械工业出版社)

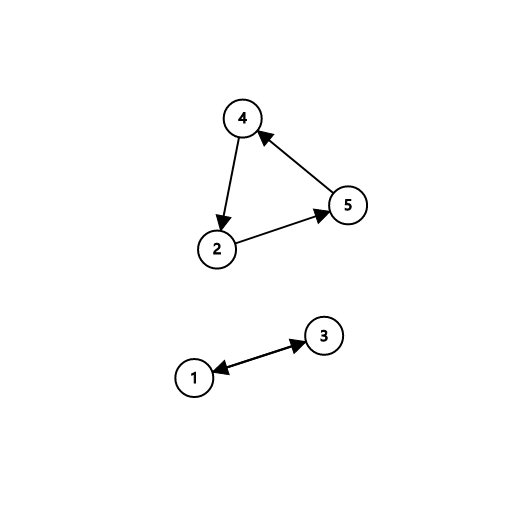

 浙公网安备 33010602011771号
浙公网安备 33010602011771号