【例题收藏】◇例题·V◇ Gap

◇例题·V◇ Gap

搜索训练开始了……POJ的数据比ZOJ强多了！！看来不得不写正解了

+传送门+

---

 

◇ 题目

<简要翻译>

有一个四行九列的矩阵——在第1~4行、2~8列上填上数字 11~17,21~27,31~37,41~47（不一定有序）。例子如下：

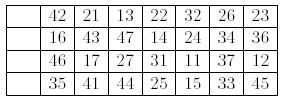
现在我们将数字11移动在第一行第一列，21移动在第二行第一列，31移动在第三行第一列，41移动在第四行第一列，上面的例子移动后如下：

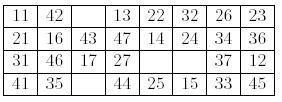
若一个数x（不是最右边的一列）的右边位置是空位，设x十位为a，个位为b，若b≠7，我们可以把数(10*a+b+1)放在右边的空格处。

比如上图的35的右边是空格，且个位是5（不是7），我们可以把36移动到右边的空格处：

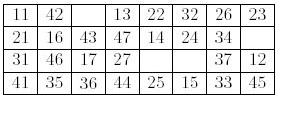
最后的目标是把矩阵变成下面这样：

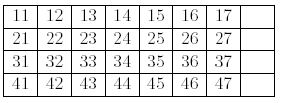
最少需要移动多少次（不包含一开始移动11,21,31,41）？

<输入输出>

包含多组数据，第一行是整数T，表示数据组数。

每组数据包含一个4*7的矩阵，表示一开始的矩阵的第1~4行、2~8列。

输出最少需要移动多少次，如果不能达到目标，输出-1。

---

 

◇ 解析

A) 准备

为了方便最后判断，先const一个常量矩阵gal，表示目标矩阵。输入过后，按照题目要求先模拟把11,21,31,41移动到第一列。

B) 哈希

算是一个矩阵Hash的模板吧……也不知道原理是什么。大概意思就是把矩阵的元素排成一列（第二行接在第一行后面，其他类似），然后将该序列的每一个元素都拆分成相等的位数。因为这道题的矩阵中的元素最大只有两位，所以只需要把每一个元素都拆分成十位和个位就行了。

然后我们得到了一个长度为cnt的序列A，则 hash=7^cnt*A[0]+7^cnt-1*A[1]+7^cnt-2*A[2]+...+7¹*A[cnt-1]+7⁰*A[cnt]

最后hash先与上一个0x7fffffff再模上一个 MOD=1000007。

ll Hash(const int A[][8]) {
	int cnt=0;
	ll ret=0,chc[105]= {};
	for(int i=0; i<4; i++)
		for(int j=0; j<8; j++)
			chc[++cnt]=A[i][j]%10,
			chc[++cnt]=A[i][j]/10;
	for(int i=1; i<=cnt; i++)
		ret=ret*7+chc[i];
	return (ret&0x7fffffff)%MOD;
}

所以我们可以把目标状态的hash值储存为ovr，则只需要判断当前状态的hash值是否是ovr就可以了。

C) BFS

普通的DFS，就像八数码一样……实在想加快的话可以用双向搜索，因为我们知道终止状态……QwQ

---

 

◇ 源代码

/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;

typedef long long ll;
const int gal[4][8]= {
	11,12,13,14,15,16,17,0,
	21,22,23,24,25,26,27,0,
	31,32,33,34,35,36,37,0,
	41,42,43,44,45,46,47,0
};
const int MOD=1000007;

struct QUEUE {
	int A[4][8],pos[4][2];
	int stp;
} beg;
bool vis[MOD+5];
int ovr;

void Clear() {
	memset(&beg,0,sizeof &beg);
	memset(vis,false,sizeof vis);
}
ll Hash(const int A[][8]) {
	int cnt=0;
	ll ret=0,chc[105]= {};
	for(int i=0; i<4; i++)
		for(int j=0; j<8; j++)
			chc[++cnt]=A[i][j]%10,
			           chc[++cnt]=A[i][j]/10;
	for(int i=1; i<=cnt; i++)
		ret=ret*7+chc[i];
	return (ret&0x7fffffff)%MOD;
}
pair<int,int> Search(int A[][8],int val) {
	for(int i=0; i<4; i++)
		for(int j=0; j<8; j++)
			if(A[i][j]==val)
				return make_pair(i,j);
}
int BFS() {
	int hash_beg=Hash(beg.A);
	if(hash_beg==ovr) return 0;
	vis[hash_beg]=true;
	queue<QUEUE> que;
	que.push(beg);
	while(!que.empty()) {
		QUEUE pre=que.front();
		que.pop();
		for(int i=0; i<4; i++)
			for(int j=0; j<7; j++)
				if(!pre.A[i][j+1]) {
					if(pre.A[i][j]%10==7 || !pre.A[i][j]) continue;
					QUEUE now=pre;
					pair<int,int> res=Search(now.A,pre.A[i][j]+1);
					swap(now.A[i][j+1],now.A[res.first][res.second]);
					now.stp++;
					int HASH=Hash(now.A);
					if(HASH==ovr) return now.stp;
					if(vis[HASH]) continue;
					vis[HASH]=true;
					que.push(now);
				}
	}
	return -1;
}
int main() {
	int T;
	scanf("%d",&T);
	ovr=Hash(gal);
	while(T--) {
		Clear();
		for(int i=0,cnt=0; i<4; i++) {
			for(int j=1; j<8; j++) {
				scanf("%d",&beg.A[i][j]);
				if(beg.A[i][j]%10==1) beg.A[i][j]=0;
			}
			beg.A[i][0]=(i+1)*10+1;
		}
		printf("%d\n",BFS());
	}
	return 0;
}

　　

---

 

The End

Thanks for reading!

- Lucky_Glass

（Tab：如果我有没讲清楚的地方可以直接在邮箱lucky_glass@foxmail.com email我，在周末我会尽量解答并完善博客~📃）