分块:优雅的暴力
分块是一种思想,通过对原数据的适当划分,并在划分后的每一个块上预处理部分信息,从而较一般的暴力算法取得更优的时间复杂度。
分块的应用面十分广泛,包括但不限于数组、树形结构等。
1. 块状数组
块状数组是分块思想最简单的应用。
它将一个数组分成若干块,然后对数组进行区间操作。对于每一个区间操作,区间中的整块可以整体处理,左右的零散块就暴力单独处理。
一般来说,我们会将一个长度为 \(n\) 的数组划分成 \(\sqrt{n}\) 块,每块长 \(\sqrt{n}\)。这样,在进行区间操作的时候,整块的处理是 \(\mathcal O(\sqrt{n})\) 的,零散块的单独处理也是 \(\mathcal O(\sqrt{n})\) 的,那么一次区间操作的复杂度即为 \(\mathcal O(\sqrt{n})\)。
显然,块状数组的效率远远不及线段树、树状数组等 \(\log\) 级别的数据结构,但是块状数组的灵活性却比这些数据结构都要强,可应用的场景也比这些数据结构多得多。
下面给出一种基础的建立块状数组的代码。这份代码对应下面的例题 1。
len = (int)sqrt(n);
int last = 0;
for(int i = 1; i <= n; i++)
{
cin >> a[i];
id[i] = (i - 1) / len + 1;
b[id[i]].sum += a[i];
if(last != id[i])
{
b[id[i - 1]].r = i - 1;
b[id[i]].l = i;
last = id[i];
}
}
b[id[n]].r = n;
例题 1 LibreOJ 6280. 数列分块入门 4
给定一个长度为 \(n\) 的序列 \(\{a_i\}\),需要执行 \(n\) 次操作。操作分为两种:
区间 \([l, r]\) 之间的所有数加上 \(x\);
求 \(\sum\limits_{i = l}^{r}{a_i} \bmod (x + 1)\)。
\(1 \le n \le 5 \times 10^4\)
考虑对序列进行分块,块长为 \(\lfloor \sqrt{n} \rfloor\)。块内维护整块的元素和 \(b_i\) 以及区间修改的标记 \(tag_i\)。这里 \(tag_i\) 记录的是每个块的整体赋值情况,这样就不用对每个块直接修改。
对于修改操作,我们分为两种情况:
-
若 \(l\) 和 \(r\) 在同一个块内,直接暴力修改,单次复杂度为 \(\mathcal O(\sqrt{n})\)。
-
若 \(l\) 和 \(r\) 不在同一个块内,则区间可分成三个部分:
-
以 \(l\) 开头的不完整块;
-
中间的若干完整块;
-
以 \(r\) 结尾的不完整块。
对于以 \(l\) 开头和 以 \(r\) 结尾的不完整块,直接暴力修改,复杂度为 \(\mathcal O(\sqrt{n})\);
对于中间的若干完整块,则修改这些完整块的整体标记 \(tag_i\),复杂度为 \(\mathcal O(\sqrt{n})\),则单次修改的复杂度为 \(\mathcal O(\sqrt{n})\)。
-
对于查询操作,我们同样分为两种情况:
-
若 \(l\) 和 \(r\) 在同一个块内,直接暴力求和,并加上修改标记,单次复杂度为 \(\mathcal O(\sqrt{n})\)。
-
若 \(l\) 和 \(r\) 不在同一个块内,则区间可分成三个部分:
-
以 \(l\) 开头的不完整块;
-
中间的若干完整块;
-
以 \(r\) 结尾的不完整块。
对于以 \(l\) 开头和 以 \(r\) 结尾的不完整块,直接暴力求和,并加上修改标记 \(tag_i\),复杂度为 \(\mathcal O(\sqrt{n})\);
对于中间的若干完整块,则将这些完整块记录的区间和 \(b_i\) 求和,加上修改标记 \(tag_i\),复杂度为 \(\mathcal O(\sqrt{n})\),则单次查询的复杂度为 \(\mathcal O(\sqrt{n})\)。
-
综上,我们即可在 \(\mathcal O(n \sqrt{n})\) 的复杂度内解决此问题。
Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e4 + 5;
int n, len, a[N], id[N];
struct node
{
int l, r, sum, tag;
}b[N];
void update(int l, int r, int w)
{
int x = id[l], y = id[r];
if(x == y)
{
for(int i = l; i <= r; i++)
a[i] += w;
b[x].sum += (r - l + 1) * w;
return;
}
for(int i = l; i <= b[x].r; i++)
a[i] += w;
b[x].sum += (b[x].r - l + 1) * w;
for(int i = b[y].l; i <= r; i++)
a[i] += w;
b[y].sum += (r - b[y].l + 1) * w;
for(int i = x + 1; i < y; i++)
b[i].tag += w;
return;
}
int query(int l, int r, int c)
{
int x = id[l], y = id[r], ans = 0;
if(x == y)
{
for(int i = l; i <= r; i++)
ans = (ans + a[i] + b[x].tag) % (c + 1);
return ans;
}
for(int i = l; i <= b[x].r; i++)
ans = (ans + a[i] + b[x].tag) % (c + 1);
for(int i = b[y].l; i <= r; i++)
ans = (ans + a[i] + b[y].tag) % (c + 1);
for(int i = x + 1; i < y; i++)
ans = (ans + b[i].sum + b[i].tag * (b[i].r - b[i].l + 1)) % (c + 1);
return ans;
}
signed main()
{
cin >> n;
len = (int)sqrt(n);
int last = 0;
for(int i = 1; i <= n; i++)
{
cin >> a[i];
id[i] = (i - 1) / len + 1;
b[id[i]].sum += a[i];
if(last != id[i])
{
b[id[i - 1]].r = i - 1;
b[id[i]].l = i;
last = id[i];
}
}
b[id[n]].r = n;
for(int i = 1; i <= n; i++)
{
int opt, l, r, w;
cin >> opt >> l >> r >> w;
if(opt == 0)
update(l, r, w);
else
cout << query(l, r, w) << "\n";
}
return 0;
}
例题 2 洛谷P2801 教主的魔法
给定一个长度为 \(n\) 的序列 \(\{a_i\}\),需要执行 \(q\) 次操作。操作分为两种:
区间 \([l, r]\) 之间的所有数加上 \(x\);
查询区间 \([l, r]\) 内大于等于 \(x\) 的数的个数。
\(n \le 10^6\),\(q \le 3000\)。
这道题比上面那道题稍难一些。
对于每一个块,我们可以将块内的元素降序排序,单独存至另一个数组 \(t\) 中。
对于查询,分为两种情况:
-
\(l\) 和 \(r\) 在同一个块中,直接暴力统计,复杂度为 \(\mathcal O(\sqrt{n})\)。
-
\(l\) 和 \(r\) 不在同一个块中。
-
对于散块,直接暴力查询,复杂度为 \(\mathcal O(\sqrt{n})\);
-
对于整块,可以对 \(t\) 进行二分,找到 \(x\) 在块中从大到小的排名,即为块中大于等于 \(x\) 的数的个数,累加起来即可。复杂度为 \(\mathcal O(\sqrt{n} \log{\sqrt{n}})\)。
那么对于查询操作,总复杂度为 \(\mathcal O(\sqrt{n} \log{\sqrt{n}})\)。
-
对于修改,同样分为两种情况
-
\(l\) 和 \(r\) 在同一个块中,直接暴力修改,然后对 \(t\) 进行重构。复杂度为 \(\mathcal O(\sqrt{n} \log{\sqrt{n}})\)。
-
\(l\) 和 \(r\) 不在同一个块中。
-
对于散块,暴力修改,并对 \(t\) 进行重构,复杂度为 \(\mathcal O(\sqrt{n} \log{\sqrt{n}})\)。
-
对于整块,直接修改标记 \(tag_i\) 即可。复杂度为 \(\mathcal O(\sqrt{n})\)。
那么修改的复杂度即为 \(\mathcal O(\sqrt{n} \log{\sqrt{n}})\)。
-
综上,我们即可在 \(\mathcal O(q\sqrt{n} \log{\sqrt{n}})\) 的复杂度内解决该问题。
Code
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
int n, m, len, a[N], t[N], id[N];
struct node
{
int l, r, tag;
}b[N];
void Sort(int x)
{
for(int i = b[x].l; i <= b[x].r; i++)
t[i] = a[i];
sort(t + b[x].l, t + 1 + b[x].r);
return;
}
void update(int l, int r, int w)
{
int x = id[l], y = id[r];
if(x == y)
{
for(int i = l; i <= r; i++)
a[i] += w;
Sort(x);
return;
}
for(int i = l; i <= b[x].r; i++)
a[i] += w;
for(int i = b[y].l; i <= r; i++)
a[i] += w;
for(int i = x + 1; i < y; i++)
b[i].tag += w;
Sort(x), Sort(y);
return;
}
int query(int l, int r, int c)
{
int ans = 0, x = id[l], y = id[r];
if(x == y)
{
for(int i = l; i <= r; i++)
if(a[i] + b[x].tag >= c)
ans++;
return ans;
}
for(int i = l; i <= b[x].r; i++)
if(a[i] + b[x].tag >= c)
ans++;
for(int i = b[y].l; i <= r; i++)
if(a[i] + b[y].tag >= c)
ans++;
for(int i = x + 1; i < y; i++)
ans += b[i].r - (lower_bound(t + b[i].l, t + 1 + b[i].r, c - b[i].tag) - t - 1);
return ans;
}
int main()
{
cin >> n >> m;
len = (int)sqrt(n);
int last = 0;
for(int i = 1; i <= n; i++)
{
cin >> a[i];
id[i] = (i - 1) / len + 1;
if(last != id[i])
{
b[id[i - 1]].r = i - 1;
b[id[i]].l = i;
last = id[i];
}
}
b[id[n]].r = n;
for(int i = len; i <= n; i += len)
Sort(id[i]);
for(int i = 1; i <= m; i++)
{
char c;
int l, r, w;
cin >> c >> l >> r >> w;
if(c == 'M')
update(l, r, w);
else
cout << query(l, r, w) << "\n";
}
return 0;
}
以上便是块状数组最简单的应用了。感兴趣的同学可以根据下面的题单进一步加强。
2. 块状链表
由于块状链表使用的并不多,所以笔者在这里只稍微提一下。
块状链表就是将一个数组分块成若干数组,然后用一个链表存起来,每个结点指向一块。
一般来说,这里的分块块长也是 \(\sqrt{n}\)。
这里放出 OI Wiki 上的一张图。
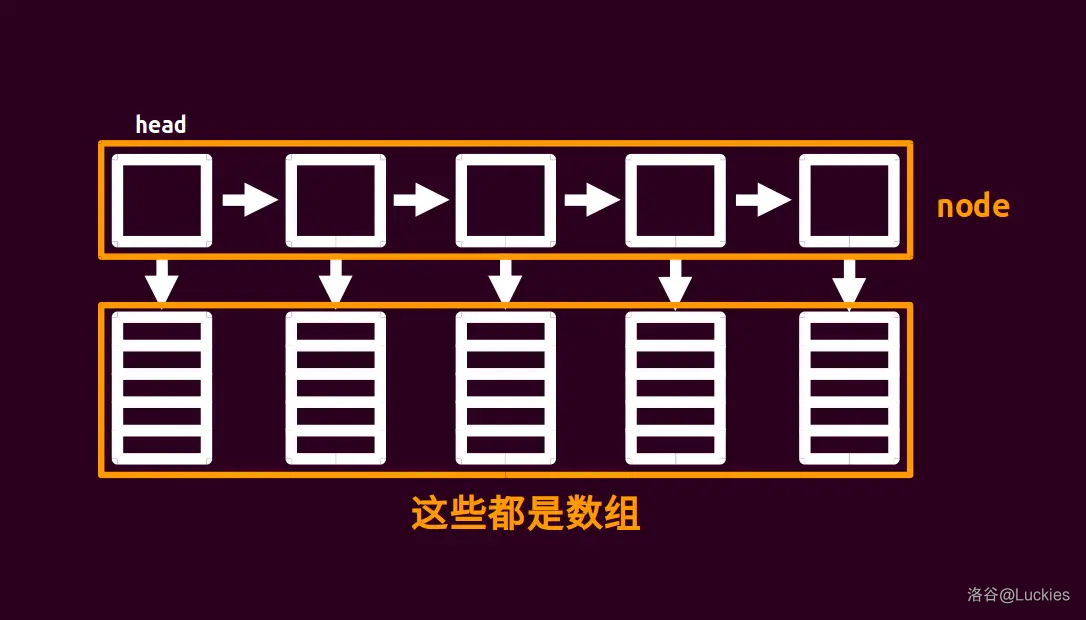
块状链表支持:分裂、插入、查找。复杂度均为 \(\mathcal O(\sqrt{n})\)。
3. 莫队算法
莫队算法是由莫涛提出的算法。莫涛提出莫队算法之前,莫队算法已经在 Codeforces 的高手圈里小范围流传,但是莫涛是第一个对莫队算法进行详细归纳总结的人。莫涛提出莫队算法时,只分析了普通莫队算法,但是经过 OIer 和 ACMer 的集体智慧改造,莫队有了多种扩展版本。
莫队算法可以解决一类离线区间询问问题,适用性极为广泛。同时将其加以扩展,便能轻松处理树上路径询问以及支持修改操作。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号