补题:CCPC Wannafly Winter Camp 2020
还是找到了很大的差距的...
假期需要努力
Day1 (暂时8/10)
Day2 (暂时9/11)
Day3 (暂时7/10)
Day5 (暂时8/10)
Day6 (暂时11/14)
Day7 (暂时6/12)
Overall
| 题号 | A | B | C | D | E | F | G | H | I | J |
| 状态 | * | * | * | o | * | * | * | * |
A. 期望逆序对
可以猜一个结论:在最优排列$p$中,$\frac{l_i+r_i}{2}$(若看成$n$条竖直线段,则为线段中心)应该单调增;证明挺显然的
之后就可以用$n^2$暴力统计$p_i,p_j$成逆序对的概率了

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef pair<int,int> pii; typedef long long ll; const int N=5005; const int MOD=998244353; inline ll quickpow(ll x,int k) { x%=MOD; ll res=1; while(k) { if(k&1) res=res*x%MOD; x=x*x%MOD; k>>=1; } return res; } inline ll rev(ll x) { return quickpow(x,MOD-2); } int n; int l[N],r[N]; int revi[N]; pii ord[N]; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d%d",&l[i],&r[i]); revi[i]=rev(r[i]-l[i]+1); ord[i]=pii(l[i]+r[i],i); } sort(ord+1,ord+n+1); ll ans=0; for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) { int ii=ord[i].second,jj=ord[j].second; ll dvd=1LL*revi[ii]*revi[jj]%MOD; ll low=max(0,l[ii]-l[jj]); ll high=max(0,min(r[ii],r[jj])-l[jj]); ll mul=1LL*(low+high)*(high-low+1)/2; mul+=1LL*max(0,r[ii]-r[jj])*(r[jj]-l[jj]+1); mul%=MOD; ans=(ans+mul*dvd)%MOD; } printf("%lld\n",ans); return 0; }
B. 密码学
反向模拟即可

#include <string> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; const int N=1005; int val[N]; char to[N]; int n,m; string s[N]; int x[N],y[N]; int main() { for(int i=0;i<26;i++) val['a'+i]=i,to[i]='a'+i; for(int i=0;i<26;i++) val['A'+i]=i+26,to[i+26]='A'+i; ios::sync_with_stdio(false); cin>>n>>m; for(int i=1;i<=m;i++) cin>>x[i]>>y[i]; for(int i=1;i<=n;i++) cin>>s[i]; while(m) { int pos=0; for(int j=0;j<s[y[m]].length();j++) { s[y[m]][j]=to[(val[s[y[m]][j]]-val[s[x[m]][pos]]+52)%52]; pos++; if(pos==s[x[m]].length()) pos=0; } m--; } for(int i=1;i<=n;i++) cout<<s[i]<<'\n'; return 0; }
C. 染色图
对于$g(n,k)$,一种比较直觉的构造方案是先把每个点的颜色确定,之后不同颜色的点互相连边
那么一共就有$n\ mod\ k$种颜色有$\lfloor \frac{n}{k}\rfloor +1$个点,有$n-(n\ mod\ k)$种颜色有$\lfloor \frac{n}{k}\rfloor$个点
所以有$g(n,k)=\frac{1}{2} \cdot [(n\text{%}k)\cdot (n- \lfloor \frac{n}{k}\rfloor -1) + (n-n\text{%}k)\cdot (n- \lfloor \frac{n}{k}\rfloor)]$
接着是求$\sum_{i=l}^{r} g(n,i)$
可以用到根号枚举的方法:对于所有的$\lfloor \frac{n}{i}\rfloor$,大于$\sqrt{n}$的最多有$\sqrt{n}$种
于是可以枚举$\lfloor \frac{n}{i}\rfloor$,对于$0\leq \lfloor \frac{n}{i}\rfloor \leq \sqrt{n}$的一并统计,对于$\sqrt{n}<\lfloor \frac{n}{i}\rfloor$的逐个枚举

#include <cmath> #include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int MOD=998244353; int main() { int T; scanf("%d",&T); while(T--) { int n,l,r; scanf("%d%d%d",&n,&l,&r); ll ans=0; int sq=sqrt(n+1); int last=l; for(int i=l;i<=min(sq,r);i++) { last=i+1; ans=(ans+1LL*n*n-n+(n/i)*i-2LL*(n/i)*n+1LL*i*(n/i)*(n/i))%MOD; } for(int i=n/sq;i>=1;i--) { int high=min(n/i,r); int low=max(n/(i+1)+1,last); if(low>r) break; if(high<last) continue; int num=high-low+1; ll sum=1LL*(low+high)*num/2%MOD; ans=(ans+1LL*n*n%MOD*num)%MOD; ans=(ans-1LL*n*num%MOD+MOD)%MOD; ans=(ans+sum*i)%MOD; ans=(ans-2LL*n*i%MOD*num%MOD+MOD)%MOD; ans=(ans+sum*i%MOD*i)%MOD; } printf("%lld\n",ans*499122177%MOD); } return 0; }
D. 生成树
(2020.2.10补)
推荐下rls的矩阵树定理笔记:kimoyami - 矩阵树定理初探
这题应该是一种比较新的套路题
考虑用使用扩展矩阵树定理,根据$G1$构造基尔霍夫矩阵$A$
枚举$G1$的每条边,若其不在$G2$内,那么边权为$1$;若在$G2$内,那么边权为$x$(变量)
删去$A$的第$n$行第$n$列得到$B$
对$B$计算行列式的值,就得到了$|B|=\sum_{i=0}^{n-1}(w_ix^i)$,其中$w_i$就是 有$i$条边在$G2$中 的生成树的个数
由于存在变量$x$,那么可以将$|B|$看做一个函数,即令$f(x)=|B|=\sum_{i=0}^{n-1}(w_ix^i)$
对$f$求导,则有$f'(x)=\sum_{i=1}^{n-1}(i\cdot w_ix^{i-1})$(由于$x^0$求导为$0$,故$i$从$1$开始)
我们惊奇的发现,$f'(1)=\sum_{i=1}^{n-1}(i\cdot w_i)$就是我们所要求的答案
于是下一个问题就是如何对行列式求导
根据 行列式的导数 - 科学空间|Scientific Spaces,有$\frac{d|B|}{dx}=|B|\sum_{i}\sum_{j} \frac{B_{ij}}{|B|}\frac{db_{ij}}{dx}$,其中$\frac{db_{ij}}{dx}$就是对$B$的每个元素分别对$x$求导
而根据代数余子式与逆矩阵的关系,有$B^{-1}=\frac{1}{|B|}B*$,即$(B^{-1})_{ij}=\frac{1}{|B|}B_{ij}$
于是可以得到$f'(x)=|B|\sum_{i}\sum_{j} (B^{-1})_{ij}\cdot \frac{db_{ij}}{dx}$
我们于是需要求三个矩阵,分别是$B$、$B$的逆矩阵、将$B$的各元素对$x$求导所构成的矩阵,然后根据上式算一下即可
复杂度为$O(n^3)$,出在对$B$求行列式值和求逆矩阵

#include <cstdio> #include <cstring> #include <cstdlib> #include <algorithm> using namespace std; const int N=405; const int MOD=998244353; inline int quickpow(int x,int k) { int res=1; while(k) { if(k&1) res=1LL*res*x%MOD; x=1LL*x*x%MOD; k>>=1; } return res; } inline int rev(int x) { return quickpow(x,MOD-2); } struct Determinant { int a[N][N<<1]; Determinant() { memset(a,0,sizeof(a)); } void add(int x,int y,int w) { a[x][x]+=w,a[y][y]+=w; a[x][y]-=w,a[y][y]-=w; } int value(int n) { int ans=1; for(int i=0;i<n;i++) for(int j=i+1;j<n;j++) while(a[j][i]) { int mul=a[i][i]/a[j][i]; for(int k=i;k<n;k++) { a[i][k]=(a[i][k]-1LL*a[j][k]*mul%MOD+MOD)%MOD; swap(a[i][k],a[j][k]); } ans=-ans; } for(int i=0;i<n;i++) ans=1LL*ans*a[i][i]%MOD; return (ans+MOD)%MOD; } int reverse(int n) { for(int i=0;i<n;i++) for(int j=n;j<2*n;j++) a[i][j]=(j-n==i?1:0); for(int i=0;i<n;i++) { int pos=i; if(pos<n && !a[pos][i]) pos++; if(pos==n) return 0; int mul=rev(a[pos][i]); for(int j=0;j<2*n;j++) { swap(a[i][j],a[pos][j]); a[i][j]=1LL*a[i][j]*mul%MOD; } for(int j=0;j<n;j++) if(j!=i) { mul=a[j][i]; for(int k=i;k<2*n;k++) a[j][k]=(a[j][k]-1LL*mul*a[i][k]%MOD+MOD)%MOD; } } for(int i=0;i<n;i++) for(int j=0;j<n;j++) a[i][j]=a[i][j+n]; return 1; } void print(int n,int mul=1) { for(int i=0;i<n;i++) for(int j=0;j<mul*n;j++) printf("%d",a[i][j]),putchar(j==mul*n-1?'\n':' '); } }A,B,C; int n; char G1[N][N],G2[N][N]; int main() { scanf("%d",&n); for(int i=0;i<n;i++) scanf("%s",G1[i]); for(int i=0;i<n;i++) scanf("%s",G2[i]); for(int i=0;i<n;i++) for(int j=0;j<n;j++) if(G1[i][j]=='1') { if(G2[i][j]=='1') C.add(i,j,1); A.add(i,j,1); } B=A; B.reverse(n-1); int ans=0; for(int i=0;i<n-1;i++) for(int j=0;j<n-1;j++) ans=(ans+1LL*B.a[i][j]*C.a[i][j])%MOD; int val=A.value(n-1); ans=1LL*ans*val%MOD; printf("%d\n",ans); return 0; }
E. 树与路径
由于不太可能一次把所有点的答案全部求出来,于是考虑先求出$1$为根时的答案,然后将根慢慢移动到相邻节点
这样就需要计算得到一个值:一次移动根以后,答案的$\Delta$
现在考虑将一个点$x$从其父亲$fa$移动而来
那么,若一条树上路径$(u_i,v_i)$不全经过$x,fa$,那么显然不会对该次移动的$\Delta$产生贡献
否则,就相当于路径的某一端长度减$1$、另一端长度加$1$
假设路径长度为$l$、到$fa$距离为$x$
那么有$\Delta =x(l-x)-(x-1)(l-x+1)=l-2x+1$,若用树上高度$dep$改写,则为$\Delta =l-2(dep[u_i]-dep[fa])+1$
从这个式子可以看出,对于一组从上向下移动的节点,那么该树上路径会使得移动的$\Delta$差$2$递减
这可以通过树上差分来解决
(具体实现需要注意细节)

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=300005; int n,m; vector<int> v[N]; int dep[N]; int to[N][20]; void dfs(int x,int fa) { to[x][0]=fa; dep[x]=dep[fa]+1; for(int i=0;i<v[x].size();i++) { int nxt=v[x][i]; if(nxt==fa) continue; dfs(nxt,x); } } int lca(int x,int y) { if(dep[y]>dep[x]) swap(x,y); for(int i=19;i>=0;i--) if(dep[to[x][i]]>=dep[y]) x=to[x][i]; if(x==y) return x; for(int i=19;i>=0;i--) if(to[x][i]!=to[y][i]) x=to[x][i],y=to[y][i]; return to[x][0]; } ll in[N][2],out[N][2]; ll dlt[N]; ll ans[N]; void push(int x,int fa) { for(int i=0;i<v[x].size();i++) { int nxt=v[x][i]; if(nxt==fa) continue; push(nxt,x); } dlt[x]=in[x][0]+in[x][1]*dep[x]; in[x][0]-=out[x][0]; in[x][1]-=out[x][1]; in[fa][0]+=in[x][0]; in[fa][1]+=in[x][1]; } void calc(int x,int fa) { ans[x]=ans[fa]+dlt[x]; for(int i=0;i<v[x].size();i++) { int nxt=v[x][i]; if(nxt!=fa) calc(nxt,x); } } int main() { scanf("%d%d",&n,&m); for(int i=1;i<n;i++) { int x,y; scanf("%d%d",&x,&y); v[x].push_back(y); v[y].push_back(x); } dfs(1,0); for(int i=1;i<20;i++) for(int j=1;j<=n;j++) to[j][i]=to[to[j][i-1]][i-1]; for(int i=1;i<=m;i++) { int x,y; scanf("%d%d",&x,&y); int anc=lca(x,y); int len=dep[x]+dep[y]-2*dep[anc]; ans[1]+=1LL*(dep[x]-dep[anc])*(dep[y]-dep[anc]); int pos; if(dep[x]-dep[anc]-1>=0) { pos=x; for(int i=0;i<20;i++) if((dep[x]-dep[anc]-1)&(1<<i)) pos=to[pos][i]; in[x][0]+=2*dep[x]-len+1; in[x][1]-=2; out[pos][0]+=2*dep[x]-len+1; out[pos][1]-=2; } if(dep[y]-dep[anc]-1>=0) { pos=y; for(int i=0;i<20;i++) if((dep[y]-dep[anc]-1)&(1<<i)) pos=to[pos][i]; in[y][0]+=2*dep[y]-len+1; in[y][1]-=2; out[pos][0]+=2*dep[y]-len+1; out[pos][1]-=2; } } push(1,0); for(int i=0;i<v[1].size();i++) calc(v[1][i],1); for(int i=1;i<=n;i++) printf("%lld\n",ans[i]); return 0; }
F. 乘法
可以二分答案
对于每次二分出的答案,可以依次枚举$A_i$、并在$B_j$中二分来实现check

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=100005; const ll INF=1000000000005LL; int n,m; ll K; ll a[N],b[N]; int main() { scanf("%d%d%lld",&n,&m,&K); for(int i=1;i<=n;i++) scanf("%lld",&a[i]); for(int i=1;i<=m;i++) scanf("%lld",&b[i]); sort(a+1,a+n+1); sort(b+1,b+m+1); ll l=-INF,r=INF,mid,ans; while(l<=r) { mid=(l+r)>>1; ll cnt=0; for(int i=1;i<=n;i++) { if(a[i]==0) { if(mid>=0) cnt+=m; continue; } ll rem=mid/a[i]; if(rem*a[i]<mid) { if((rem+1)*a[i]>=mid) rem++; if((rem-1)*a[i]>=mid) rem--; } if((rem+1)*a[i]>=mid) { int p=lower_bound(b+1,b+m+1,rem)-b; cnt+=m+1-p; } else { int p=upper_bound(b+1,b+m+1,rem)-b; cnt+=p-1; } } if(cnt>=K) { ans=mid; l=mid+1; } else r=mid-1; } printf("%lld\n",ans); return 0; }
G. 圆凸包
待补,需要学习凸包等平面几何基础知识
H. 最大公约数
题面有点绕
假设$k=p_1^{a_1}\cdot ... \cdot p_m^{a_m}$,那么若令$y=p_1^{a_1+1}\cdot ... \cdot p_m^{a_m+1}$,只要有$gcd(x,y)\neq k$,就能判断A撒谎
不过由于$k<=n$,所以当$k$与某质因数$p_i$的乘积$k\cdot p_i>n$时,显然不会有$gcd(x,y)=k\cdot p_i$
那么答案$y$中该质因数的次数仍为$a_i$而不是$a_i+1$

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; const int N=1000; int p[1005]; vector<int> prime; int n,k; int top; long long val[100005]; int main() { for(int i=2;i<N;i++) if(!p[i]) { prime.push_back(i); for(int j=i+i;j<N;j+=i) p[j]=true; } int T; scanf("%d",&T); while(T--) { scanf("%d%d",&n,&k); memset(val,0,sizeof(val)); top=0; val[top]=k; for(int i=0;i<prime.size();i++) { if(prime[i]>n) break; if(k*prime[i]<=n) { for(int j=0;j<=top;j++) val[j]*=prime[i]; bool flag=false; for(int j=0;;j++) { if(j>top && !flag) break; top=max(top,j); flag=false; if(val[j]>9) flag=true; val[j+1]+=val[j]/10; val[j]%=10; } } } for(int i=top;i>=0;i--) printf("%lld",val[i]); printf("\n"); } return 0; }
I. K小数查询
std做法待补
区间修改一般是线段树的活,所以加上$K$小数查询总会很麻烦,更何况这里的区间修改是jls线段树的那种
所以可以考虑根号分块,每一块内部先排好序(但需要存一下原来的位置)
那么对于修改操作,在两端暴力改、在中间块打上标记
对于查询操作,可以二分答案,然后在两端暴力数、在中间块二分
时间复杂度$O(\sqrt{n}q\cdot (logn)^2)$,不过实际能过
如果时限严格一点的话,由于修改和查询的时间复杂度不同,可以平衡一下块的长度,使得修改和查询的复杂度均约为一个log

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef pair<int,int> pii; const int N=80005; const int SQ=300; int n,m; int lim[SQ]; vector<pii> v[SQ]; vector<int> tmp; inline int check(int l,int r,int x) { int cnt=upper_bound(tmp.begin(),tmp.end(),x)-tmp.begin(); if(l==r) return cnt; for(int i=l+1;i<r;i++) if(x>=lim[i]) cnt+=(int)v[i].size(); else cnt+=upper_bound(v[i].begin(),v[i].end(),pii(x,n))-v[i].begin(); return cnt; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { int x; scanf("%d",&x); v[i/SQ].push_back(pii(x,i)); } for(int i=1/SQ;i<=n/SQ;i++) { lim[i]=1<<30; sort(v[i].begin(),v[i].end()); } while(m--) { int op,l,r,x; scanf("%d%d%d%d",&op,&l,&r,&x); if(op==1) { int low=l/SQ,high=r/SQ; for(int i=0;i<v[low].size();i++) if(v[low][i].second>=l && v[low][i].second<=r) v[low][i].first=min(v[low][i].first,x); for(int i=0;i<v[high].size();i++) if(v[high][i].second>=l && v[high][i].second<=r) v[high][i].first=min(v[high][i].first,x); sort(v[low].begin(),v[low].end()); sort(v[high].begin(),v[high].end()); for(int i=low+1;i<high;i++) lim[i]=min(lim[i],x); } else { tmp.clear(); int low=l/SQ,high=r/SQ; for(int i=0;i<v[low].size();i++) if(v[low][i].second>=l && v[low][i].second<=r) tmp.push_back(min(v[low][i].first,lim[low])); if(low!=high) for(int i=0;i<v[high].size();i++) if(v[high][i].second>=l && v[high][i].second<=r) tmp.push_back(min(v[high][i].first,lim[high])); sort(tmp.begin(),tmp.end()); int l=1,r=1000000000,mid; while(l<r) { mid=(l+r)>>1; if(check(low,high,mid)>=x) r=mid; else l=mid+1; } printf("%d\n",l); } } return 0; }
J. 德州扑克
待补
Overall
| 题号 | A | B | C | D | E | F | G | H | I | J | K |
| 状态 | * | * | * | o | * | * | * | * | * |
A. 托米的字符串
这题应该有不少做法,不过感觉std的比较优秀
首先考虑长度为$1$的所有子串,显然若当前字母为元音字母则贡献为$1$;记一共有$f[1]$个元音字母
然后考虑对所有长度为$1$的子串后面补一个字母,此时其中的元音字母数量之和就是$s_1,...,s_{n-1}$和$s_2,...,s_n$中的元音数量;则所有长度为$2$的子串中,元音字母总数量为$f[2]=f[1]+(s_2,...,s_{n-1}\text{中元音数量})$
之后都是类似的

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=1000010; int n; char s[N]; int p[200]; int cnt[N]; ll f[N]; int main() { p['a']=p['e']=p['i']=p['o']=p['u']=p['y']=1; scanf("%s",s+1); n=strlen(s+1); for(int i=1;i<=n;i++) cnt[i]=cnt[i-1]+p[s[i]]; f[1]=cnt[n]; for(int i=2;i<=n;i++) f[i]=f[i-1]+cnt[n-i+1]-cnt[i-1]; double ans=0.0; for(int i=1;i<=n;i++) ans+=double(f[i])/i; ans=ans*2.0/n/(n+1); printf("%.10f\n",ans); return 0; }
B. 萨博的方程式
这应该是我接触数位dp的第一题?rls把我教懂的
考虑将所有的$x_i$用二进制表示,并且补齐前导$0$使之对齐
那么可能一部分$x_i$在最高位为$0$,其余的为$1$
对于最高位为$0$的那些$x_i$,因为不可能填$1$,所以暂时不考虑
那么唯一需要做决定的就是那些最高位为$1$的$x_i$;我们需要考虑它们要填$1$还是$0$
可以确定:只要将一个可以填$0$的$x_i$填成$1$,那么我们可以保证一定能存在解,因为最高位之后的所有位都没有限制,所以可以根据其他数的填法最后补救
而对于下一个这样的数,若记最高位为$2^k$项,那么将产生$2^k-1$倍的贡献,因为后面的位可以随便填
而对于只能填$0$、或是最高位选择了$1$的$x_i$,能够分别产生$x_i,x_i-2^k+1$倍的贡献,因为需要在限制范围内选择数
于是可以对于最高位动态规划
记$dp[i][j]$表示前$i$个数中,有$j$个数本来可能填$1$、但最终填了$0$
若第$i$个数在最高位填$1$,则向后转移$dp[i+1][j]=dp[i+1][j]+dp[i][j]\cdot (x_i-2^k+1)$(对于$dp[i][1]$需要特殊考虑)
若第$i$个数在最高位填$0$,则向后转移$dp[i+1][j+1]=dp[i+1][j+1]+dp[i][j]\cdot 2^k$
根据$K$选择符合条件的$dp[n+1][j]$累加即可
若当前位数所有可供选择的$x_i$均填了$1$,那么就转化为了次高位的问题了(因为仅根据最高位无法保证有解),完全一样的dp下去即可

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=55; const ll MOD=1000000007; int n; ll K; ll a[N]; ll dp[N][N]; int main() { while(~scanf("%d%lld",&n,&K)) { for(int i=1;i<=n;i++) scanf("%lld",&a[i]); ll ans=0; for(int i=35;i>=0;i--) { memset(dp,0LL,sizeof(dp)); dp[1][0]=1; ll xorsum=0,other=1,before=1; for(int j=1;j<=n;j++) { ll cur=a[j]&(1LL<<i); ll rem=(a[j]&((1LL<<i)-1))+1; xorsum^=cur; if(cur) { dp[j+1][1]=(dp[j+1][1]+before)%MOD; for(int k=1;k<=n;k++) { dp[j+1][k+1]=(dp[j+1][k+1]+dp[j][k]*(1LL<<i))%MOD; dp[j+1][k]=(dp[j+1][k]+dp[j][k]*rem)%MOD; } before=before*rem%MOD; } else { other=1LL*other*rem%MOD; for(int k=0;k<=n;k++) dp[j+1][k]=(dp[j+1][k]+dp[j][k])%MOD; } } ll sum=0; for(int j=((K&(1<<i))^xorsum)?1:2;j<=n;j+=2) sum=(sum+dp[n+1][j]*other)%MOD; ans+=sum; if(xorsum!=(K&(1LL<<i))) break; if(i==0) ans++; } printf("%lld\n",ans%MOD); } return 0; }
C. 纳新一百的石子游戏
题目相当于求有多少种取法可以使剩余石子的xor值为$0$
记$sum=a_1\ xor\ ...\ xor\ a_i$,那么就是求满足$a_j\geq sum\ xor\ a_j,1\leq j\leq i$的$j$的数量
为了计算上式,我们可以考虑比较$a_j$与$sum$在二进制下的形式
若$a_j$的位数小于$sum$的,那么$sum\ xor\ a_j$的位数依然大于$a_j$的,则上式必然不满足
若$a_j$的位数等于$sum$的,那么$sum\ xor\ a_j$的位数显然小于$a_j$的,则上式必然满足
若$a_j$的位数大于$sum$的,那么$sum\ xor\ a_j$的位数与$a_j$的相同,那么就需要知道$sum$的最高位是否在$a_j$中为$1$;为$1$时则上式满足,否则不满足
不过需要特判$sum=0$的情况,此时先手必败

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=100005; int n; ll a[N]; int num[70]; int cnt[70]; int len(ll x) { if(x==0) return -1; int res=0; x>>=1; while(x) { x>>=1; res++; } return res; } int main() { scanf("%d",&n); ll sum=0; for(int i=1;i<=n;i++) { scanf("%lld",&a[i]); sum^=a[i]; int lensum=len(sum); int lena=len(a[i]); num[lena]++; for(int j=0;j<lena;j++) { ll val=a[i]&(1LL<<j); if(val==0) continue; cnt[j]++; } int res=0; if(lensum>=0) { res=num[lensum]; res+=cnt[lensum]; } printf("%d\n",res); } return 0; }
D. 卡拉巴什的字符串
(2022.9.10补)
详见 这里。
E. 阔力梯的树
这种逐子树统计的题目显然是dsu on tree
对于每个子树内结实程度的计算,用set维护一下子树内的$a_i$即可
set内的操作有点麻烦(找前驱、后继什么的)

#include <set> #include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=100005; int n; int p[N]; vector<int> v[N]; int sz[N],son[N]; void dfs(int x) { sz[x]=1; for(int i=0;i<v[x].size();i++) { int nxt=v[x][i]; dfs(nxt); sz[x]+=sz[nxt]; if(!son[x] || sz[son[x]]<sz[nxt]) son[x]=nxt; } } ll res,ans[N]; set<int> s; inline ll pw(ll x) { return x*x; } void add(int x,int tag) { int low=-1,high=-1; if(s.size()>0 && *s.begin()<x) low=*(--s.lower_bound(x)); if(s.size()>0 && *s.rbegin()>x) high=*s.upper_bound(x); if(tag==0) { if(low<0 && high>=0) res-=pw(high-x); if(low>=0 && high<0) res-=pw(x-low); if(low>=0 && high>=0) res=res-pw(high-x)-pw(x-low)+pw(high-low); s.erase(s.find(x)); } else { if(low<0 && high>=0) res+=pw(high-x); if(low>=0 && high<0) res+=pw(x-low); if(low>=0 && high>=0) res=res-pw(high-low)+pw(high-x)+pw(x-low); s.insert(x); } } void traverse(int x,int tag) { add(x,tag); for(int i=0;i<v[x].size();i++) traverse(v[x][i],tag); } void solve(int x,int keep) { for(int i=0;i<v[x].size();i++) { int nxt=v[x][i]; if(nxt!=son[x]) solve(nxt,0); } if(son[x]) solve(son[x],1); for(int i=0;i<v[x].size();i++) { int nxt=v[x][i]; if(nxt!=son[x]) traverse(nxt,1); } add(x,1); ans[x]=res; if(!keep) traverse(x,0); } int main() { scanf("%d",&n); for(int i=2;i<=n;i++) { scanf("%d",&p[i]); v[p[i]].push_back(i); } dfs(1); solve(1,1); for(int i=1;i<=n;i++) printf("%lld\n",ans[i]); return 0; }
F. 采蘑菇的克拉莉丝
有点麻烦,之后组织一下语言

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; typedef pair<int,int> pii; const int N=1000005; struct SegTree { int sz; ll *t; void init(int in) { sz=1; while(sz<in) sz<<=1; t=new ll[sz<<1|1]; for(int i=0;i<(sz<<1);i++) t[i]=0; } ~SegTree() { delete []t; } inline void pushdown(int x) { if(x>=sz) return; t[x<<1]+=t[x]; t[x<<1|1]+=t[x]; t[x]=0; } void add(int k,int l,int r,int a,int b,int x) { pushdown(k); if(a>r || b<l) return; if(a>=l && b<=r) { t[k]+=x; return; } int mid=(a+b)>>1; add(k<<1,l,r,a,mid,x); add(k<<1|1,l,r,mid+1,b,x); } ll query(int k,int p,int a,int b) { pushdown(k); if(a==b) return t[k]; int mid=(a+b)>>1; if(p<=mid) return query(k<<1,p,a,mid); else return query(k<<1|1,p,mid+1,b); } }T[N]; int n,m; vector<pii> v[N]; int val[N]; int fa[N],dep[N],sz[N],son[N]; void dfs1(int x,int f) { sz[x]=1; fa[x]=f; dep[x]=dep[f]+1; for(int i=0;i<v[x].size();i++) { int nxt=v[x][i].first,cost=v[x][i].second; if(nxt==f) continue; val[nxt]=cost; dfs1(nxt,x); sz[x]+=sz[nxt]; if(!son[x] || sz[son[x]]<sz[nxt]) son[x]=nxt; } } int tot; int id[N],top[N]; int pos[N]; vector<int> sp[N]; vector<ll> spv[N]; void dfs2(int x,int t) { top[x]=t; if(x==t) { id[x]=++tot,pos[x]=1; sp[id[x]].push_back(0); } else id[x]=id[t],pos[x]=pos[fa[x]]+1; sp[id[x]].push_back(x); if(son[x]) dfs2(son[x],t); else T[id[x]].init(pos[x]); for(int i=0;i<v[x].size();i++) { int nxt=v[x][i].first; if(nxt==fa[x] || nxt==son[x]) continue; dfs2(nxt,nxt); } } ll num[N]; ll mul,pool[N],poolflow[N]; int main() { scanf("%d",&n); for(int i=1;i<n;i++) { int x,y,w; scanf("%d%d%d",&x,&y,&w); v[x].push_back(pii(y,w)); v[y].push_back(pii(x,w)); } dfs1(1,0); dfs2(1,1); int curpos=1; scanf("%d",&m); while(m--) { int op,x,y; scanf("%d",&op); if(op==1) { scanf("%d%d",&x,&y); mul+=y; poolflow[x]+=y; int cur=x,to; while(1) { to=top[cur]; T[id[cur]].add(1,1,pos[cur],1,T[id[cur]].sz,y); if(to==1) break; pool[fa[to]]+=1LL*val[to]*y; poolflow[fa[to]]+=y; cur=fa[to]; } } else { scanf("%d",&x); curpos=x; } x=curpos; ll add=mul; int idx=id[x]; ll sub=T[idx].query(1,pos[x],1,T[idx].sz); ll ans=(add-sub)*val[x]; if(pos[x]!=(int)sp[id[x]].size()-1) ans+=(sub-poolflow[x])*val[sp[id[x]][pos[x]+1]]; ans+=pool[x]; printf("%lld\n",ans); } return 0; }
G. 糖糖王国的道路修建
待补,需要学习凸包和三角剖分等平面几何知识
H. 叁佰爱抠的序列
相当于对于一个无向满图,构造一种方案使得至少访问每条边一次
当该图的点数为奇数时,每个点都为偶度点,那么一定存在欧拉回路;构造方法就是从$n=3$时一次加两个点慢慢构造
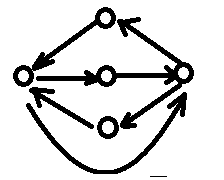
当该图的点数为偶数时,那么不存在欧拉回路,需要增加$\frac{n}{2}-1$条边来消除奇度点;具体做法是从$n=2$时一次加两个点构造
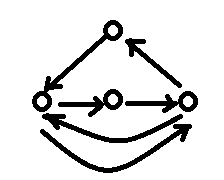
至于一开始满图点数的判断,大约在$\sqrt{2n}$左右检验一下即可

#include <cmath> #include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int LIM=2000000; ll n; int a[LIM+5]; int main() { scanf("%lld",&n); ll m=sqrt(2*n),ans; while(m*(m+1)/2+1>n) --m,ans=m; while(m*(m+1)/2+1<=n) ans=m,m++; if(ans&1) if(ans*(ans+1)/2+ans/2+1>n) ans--; printf("%lld\n",ans+1); if(n>LIM) return 0; if(ans==0) { printf("1\n"); return 0; } int i=0; if(ans&1) { a[++i]=2,a[++i]=1; for(int j=3;j<=ans;j+=2) { a[++i]=j; for(int k=2;k<j;k++) if(k&1) a[++i]=k,a[++i]=j; else a[++i]=k,a[++i]=j+1; a[++i]=j,a[++i]=j+1,a[++i]=1; } } else { a[++i]=1,a[++i]=2,a[++i]=3,a[++i]=1; for(int j=4;j<=ans;j+=2) { a[++i]=j; for(int k=2;k<j;k+=2) a[++i]=k,a[++i]=j+1,a[++i]=k+1,a[++i]=j; a[++i]=j+1,a[++i]=1; } } for(int j=1;j<=i;j++) printf("%d",a[j]),putchar(j<n?' ':'\n'); for(int j=i+1;j<=n;j++) putchar('1'),putchar(j<n?' ':'\n'); return 0; }
I. 堡堡的宝藏
待补,需要学习KM的原理,顺便掌握用单纯型求解的办法
J. 邦邦的2-SAT模板
这个模板的问题在于,当确定一个点的边需要很深的递归、且该递归的结果是矛盾时会使得复杂度为$n^2$
一个$U$形的连边方式就会造成这种结果

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; int main() { int n; scanf("%d",&n); printf("%d\n",n); for(int i=1;i<n;i++) printf("%d %d\n",-i,i+1); printf("%d %d\n",-n,-n); return 0; }
K. 破忒头的匿名信
根据词典建立AC自动机
我们相当于需要将信件内容T剪成几个单词,而判断当前位置是否可能为单词结尾的方法是:不停向fail上跳并检验是否为叶节点
记$dp[i]$表示直到第$i$个字符需要的最小代价
则转移方程为$dp[i]=dp[j]+cost(j+1,i)$,其中$j$是一个可向$i$转移的位置
由于fail树上跳的次数不会很多,所以可以直接dp

#include <queue> #include <string> #include <cstdio> #include <vector> #include <cstring> #include <iostream> #include <algorithm> using namespace std; typedef long long ll; const int N=500005; int n; int p[N]; string s[N]; string t; int tot; int id[N]; int to[N][26],fail[N]; queue<int> Q; ll dp[N]; int main() { ios::sync_with_stdio(false); cin>>n; for(int i=1;i<=n;i++) cin>>s[i]>>p[i]; cin>>t; for(int i=1;i<=n;i++) { int cur=0; for(int j=0;j<s[i].length();j++) { int val=s[i][j]-'a'; if(!to[cur][val]) to[cur][val]=++tot; cur=to[cur][val]; } if(!id[cur] || p[id[cur]]>p[i]) id[cur]=i; } for(int i=0;i<26;i++) if(to[0][i]) Q.push(to[0][i]); while(!Q.empty()) { int cur=Q.front(); Q.pop(); for(int i=0;i<26;i++) { int nxt=to[cur][i]; if(nxt) { int pos=fail[cur]; while(pos && !to[pos][i]) pos=fail[pos]; if(to[pos][i]) fail[nxt]=to[pos][i]; Q.push(nxt); } } } int cur=0; for(int i=0;i<t.length();i++) { int val=t[i]-'a'; while(cur && !to[cur][val]) cur=fail[cur]; if(to[cur][val]) cur=to[cur][val]; int pos=cur; while(pos) { if(id[pos]) { int last=i+1-s[id[pos]].length(); if(last!=0 && dp[last]==0) { pos=fail[pos]; continue; } ll w=dp[last]+p[id[pos]]; if(dp[i+1]==0 || dp[i+1]>w) dp[i+1]=w; } pos=fail[pos]; } } if(dp[t.length()]==0) printf("-1\n"); else printf("%lld\n",dp[t.length()]); return 0; }
Overall
| 题号 | A | B | C | D | E | F | G | H | I | J |
| 状态 | * | * | * | * | * | o | o |
A. 黑色气球
特殊情况是$n=2$
由于数据保证答案唯一,所以气球个数均为$1$

#include <cstdio> #include <cstring> using namespace std; typedef long long ll; const int N=1005; int n; ll a[N][N],sum; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) scanf("%lld",&a[i][j]),sum+=a[i][j]; if(n==2) { printf("1 1\n"); return 0; } ll one=sum/2/(n-1); for(int i=1;i<=n;i++) { ll add=0; for(int j=1;j<=n;j++) add+=a[i][j]; printf("%lld",(add-one)/(n-2)); if(i!=n) putchar(' '); } return 0; }
B. 小吨的点分治
待补
C. 无向图定向
显然最长路在任何时候都不可能超过$n$(极端情况是完全图)
每次考虑在当前的点集外加入一个最大独立集,使得最长路径$+1$
由于整个图中的极大独立集数量不大,所以可以先预处理出来,然后通过$O(2^n\cdot size)$的bfs得到答案($size$为极大独立集数量)

#include <queue> #include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; const int N=20; int n,m; int full; int to[N]; int cur,cover; vector<int> ind; void dfs(int x) { int save=cover; bool flag=false; for(int i=x+1;i<=n;i++) { if(cover&(1<<i)) continue; flag=true; cur^=(1<<i); cover=(save|to[i]); dfs(i); cur^=(1<<i); cover=save; } if(!flag) { if((cover^full^1)&((1<<x)-1)) return; ind.push_back(cur); } } int d[1<<N]; queue<int> Q; int main() { scanf("%d%d",&n,&m); full=(1<<(n+1))-1; for(int i=1;i<=n;i++) to[i]|=(1<<i); for(int i=1;i<=m;i++) { int x,y; scanf("%d%d",&x,&y); to[x]|=(1<<y); to[y]|=(1<<x); } dfs(0); for(int i=0;i<=full;i++) d[i]=N; d[0]=0; Q.push(0); while(!Q.empty()) { int mask=Q.front(); Q.pop(); for(int i=0;i<ind.size();i++) { int nmask=(mask|ind[i]); if(d[nmask]>d[mask]+1) { d[nmask]=d[mask]+1; Q.push(nmask); } } } printf("%d\n",d[full^1]-1); return 0; }
D. 求和
待补,需要掌握莫比乌斯反演
E. 棋技哥
题意即求最小操作步数
考虑最右下角的一个黑色格子,若想将它变成白色,那么就需要在以它为左上角的矩形中进行一次操作
但是由于已经认为它是最右下角的黑格子,所以如果不在该点操作,就会产生在它右下角的新黑色格子,那么一定不是最优操作的情况
于是就可以按照顺序从下至上、从右至左地依次在黑色格子处操作即可

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=505; int n,m; char a[N][N]; int col[N]; int main() { int T; scanf("%d",&T); while(T--) { memset(col,0,sizeof(col)); scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) { a[i][j]=getchar(); while(a[i][j]<'0' || a[i][j]>'1') a[i][j]=getchar(); } int cnt=0; for(int i=n;i>=1;i--) { int sum=0; for(int j=m;j>=1;j--) { sum+=col[j]; if(((a[i][j]=='1')+sum)&1) col[j]++,cnt++,sum++; } } printf((cnt&1)?"call\n":"aoligei\n"); } return 0; }
F. 社团管理
经典的决策单调性问题
这里是待决策点不会成为决策点的情况,所以可以类似整体二分处理
但是$c(i,j)$无法预处理,所以用类似莫队的方法每次查询时暴力移动两端点即可
板子一拖就行了

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=100005; const int K=25; int n,k; int a[N]; ll sum; int lb,rb; int cnt[N]; inline ll w(int l,int r) { while(lb>l) { sum+=cnt[a[--lb]]; cnt[a[lb]]++; } while(rb<r) { sum+=cnt[a[++rb]]; cnt[a[rb]]++; } while(lb<l) { cnt[a[lb]]--; sum-=cnt[a[lb++]]; } while(rb>r) { cnt[a[rb]]--; sum-=cnt[a[rb--]]; } return sum; } ll dp[K][N]; //l,r: 被决策点的下/上界 //L,R: 决策点的下/上界 void Solve(int i,int l,int r,int L,int R) { if(l>r) return; // mid: [l,r]中二分被决策点 // pos: mid的决策点 int pos=-1,mid=(l+r)>>1; for(int j=L;j<=min(mid-1,R);j++) { ll val=dp[i-1][j]+w(j+1,mid); if(val<dp[i][mid]) dp[i][mid]=val,pos=j; } Solve(i,l,mid-1,L,pos); Solve(i,mid+1,r,pos,R); } int main() { scanf("%d%d",&n,&k); for(int i=1;i<=n;i++) scanf("%d",&a[i]); for(int i=0;i<=k;i++) for(int j=0;j<=n;j++) dp[i][j]=1LL<<60; dp[0][0]=0; for(int i=1;i<=k;i++) { sum=0; lb=1,rb=0; memset(cnt,0,sizeof(cnt)); Solve(i,1,n,0,n-1); } printf("%lld\n",dp[k][n]); return 0; }
G. 火山哥周游世界
std是虚树和最远点的思路,待补
(2020.2.20留言:破案了,根本不需要用虚树,树形dp求的就是最远点)
不过用树形dp也很容易处理
考虑以$1$为起点,到达$K$个点的最小代价,这是一个挺经典的树形dp问题
用$dp[i][j]$表示,从$i$点出发,访问其所有子树中的需访问国家,返回/不返回$i$点所需要的代价;$j=0$表示不返回,$j=1$表示返回
这样一来,从$1$为起点的答案已经得到了,但是以其他顶点为起点的答案还无法得到
可以发现,对于其他点$i$,如果将其提为根,那么 原来为$i$儿子的子树信息 在求解$1$为起点时已经得到了,唯一缺少的信息是 原来其父亲的子树内情况
这个可以再通过一次树形dp从$1$向下转移
于是每个点的答案就可以综合两次dp的信息得到

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef pair<int,int> pii; typedef long long ll; const int N=500005; int n,m; int ff[N]; vector<pii> v[N]; bool flag[N]; ll up[N][2],down[N][2]; void pushup(int x,int fa) { ff[x]=fa; ll sum=0,maxdiff=0; for(int i=0;i<v[x].size();i++) { int nxt=v[x][i].first,cost=v[x][i].second; if(nxt==fa) continue; pushup(nxt,x); flag[x]|=flag[nxt]; if(!flag[nxt]) continue; ll one=down[nxt][1]+cost*2; ll zero=down[nxt][0]+cost; sum+=one; maxdiff=max(maxdiff,one-zero); } down[x][1]=sum; down[x][0]=sum-maxdiff; } void pushdown(int x,int fa) { ll sum=up[x][1],max1=up[x][1]-up[x][0],max2=0,son=0; for(int i=0;i<v[x].size();i++) { int nxt=v[x][i].first,cost=v[x][i].second; if(nxt==fa || !flag[nxt]) continue; son=nxt; ll one=down[nxt][1]+cost*2; ll zero=down[nxt][0]+cost; sum+=one; if(max2<one-zero) max2=one-zero; if(max2>max1) swap(max1,max2); } for(int i=0;i<v[x].size();i++) { int nxt=v[x][i].first,cost=v[x][i].second; if(nxt==fa) continue; ll one=0,zero=0; if(flag[nxt]) { one=down[nxt][1]+cost*2; zero=down[nxt][0]+cost; } up[nxt][1]=sum-one+cost*2; up[nxt][0]=sum-one-(max1==one-zero?max2:max1)+cost; } for(int i=0;i<v[x].size();i++) { int nxt=v[x][i].first,cost=v[x][i].second; if(nxt==fa) continue; pushdown(nxt,x); } } int main() { scanf("%d%d",&n,&m); for(int i=1;i<n;i++) { int x,y,w; scanf("%d%d%d",&x,&y,&w); v[x].push_back(pii(y,w)); v[y].push_back(pii(x,w)); } for(int i=1;i<=m;i++) { int x; scanf("%d",&x); flag[x]=true; } pushup(1,0); pushdown(1,0); for(int i=1;i<=n;i++) { ll sum=up[i][1],maxdiff=up[i][1]-up[i][0]; for(int j=0;j<v[i].size();j++) { int nxt=v[i][j].first,cost=v[i][j].second; if(nxt==ff[i] || !flag[nxt]) continue; ll one=down[nxt][1]+cost*2; ll zero=down[nxt][0]+cost; sum+=one; maxdiff=max(maxdiff,one-zero); } printf("%lld\n",sum-maxdiff); } return 0; }
H. 火山哥的序列
(2020.1.23补)
题目的转化思想还是很优秀的,学到了
考虑枚举gcd,那么根据埃氏筛,可以在均摊$log$的时间内找出所有该gcd的倍数
那么考虑在什么情况下该gcd可能对答案产生贡献(即成为一对所枚举$(i,j)$的$g(i,j)$):
如果转化一下思路、将区间问题转化为边界问题,其实仅仅有三种情况
如记该gcd的倍数在$a$数组中的出现位置为$pos_1,pos_2,...,pos_m$,那么被删去区间$(i,j)$满足
(1) 不包含$pos_1,pos_2$:此时$j<pos_1$(被情况(3)包含)或$i>pos_2$
(2) 不包含$pos_1,pos_m$:此时$i>pos_1,j<pos_m$
(3) 不包含$pos_{m-1},pos_m$:此时$j<pos_{m-1}$或$i>pos_m$(被情况(1)包含)
于是考虑用线段树对于每一个$i$,直接求所有$i\leq j\leq n$的$\sum g(i,j)$:
$query(j,j)$(即单点查询$j$)表示:在删去区间左端点为$i$、右端点为$j$时,$g(i,j)=query(j,j)$
如果线段树支持区间和,那么$query(i,n)$就是所有左端点为$i$的答案
考虑初始情况下$i=1$,那么此时观察上面的$3$个条件,仅有(3)可能满足
所以在初始情况下,仅需要在上面枚举gcd时对线段树实现区间取max,即令$t_j=max(t_j,gcd),j<pos_{m-1}$
然后,当我们已经加过$i=1$时的答案后,考虑利用条件(1)、(2)更新线段树上的权值
可以在上面枚举gcd时,将(1)、(2)条件分别塞到下标为$pos_2$、$pos_1$的vector中,操作依次是 令$t_j=max(t_j,gcd),j>pos_2$、令$t_j=max(t_j,gcd),j<pos_m$
区间取max可以用jls线段树实现,可参考我的学习笔记
这道题还是很值得学习的;之前以为jls线段树仅会出现在硬核数据结构题中,没想到会有这么巧妙的形式

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; typedef pair<int,int> pii; const int N=200005; struct Node { int x,y,cnt; ll sum; Node(int a=0,int b=N,int c=1,ll d=0LL) { x=a,y=b,cnt=c,sum=d; } }; int sz; Node t[N<<2]; //将儿子信息合并 inline void pushup(int k) { int l=k<<1,r=k<<1|1; t[k].sum=t[l].sum+t[r].sum; if(t[l].x==t[r].x) { t[k].x=t[l].x; t[k].y=min(t[l].y,t[r].y); t[k].cnt=t[l].cnt+t[r].cnt; } else { if(t[l].x>t[r].x) swap(l,r); t[k].x=t[l].x; t[k].y=min(t[l].y,t[r].x); t[k].cnt=t[l].cnt; } } //用x更新区间:t[k].x<x<t[k].y inline void dec(int k,int x) { if(t[k].x>=x) return; t[k].sum+=1LL*t[k].cnt*(x-t[k].x); t[k].x=x; } inline void pushdown(int k) { dec(k<<1,t[k].x); dec(k<<1|1,t[k].x); } void build(int k,int l,int r,int a,int b) { if(a==b) { t[k]=Node(); return; } int mid=(a+b)>>1; build(k<<1,l,r,a,mid); build(k<<1|1,l,r,mid+1,b); pushup(k); } void modify(int k,int l,int r,int a,int b,int x) { if(a>r || b<l) return; if(a>=l && b<=r) { if(t[k].x>=x) return; if(t[k].y>x) { dec(k,x); return; } } pushdown(k); int mid=(a+b)>>1; modify(k<<1,l,r,a,mid,x); modify(k<<1|1,l,r,mid+1,b,x); pushup(k); } ll query(int k,int l,int r,int a,int b) { if(a>r || b<l) return 0; if(a>=l && b<=r) return t[k].sum; pushdown(k); int mid=(a+b)>>1; return query(k<<1,l,r,a,mid)+query(k<<1|1,l,r,mid+1,b); } int n; int a[N],rev[N]; int cnt,pos[N]; vector<pii> v[N]; int main() { int T; scanf("%d",&T); while(T--) { memset(rev,0,sizeof(rev)); scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]),rev[a[i]]=i; sz=1; while(sz<n) sz<<=1; build(1,1,n,1,sz); for(int i=1;i<N;i++) { cnt=0; for(int j=i;j<N;j+=i) if(rev[j]) pos[++cnt]=rev[j]; sort(pos+1,pos+cnt+1); if(cnt>1) { modify(1,1,pos[cnt-1]-1,1,sz,i); v[pos[1]].push_back(pii(-pos[cnt]+1,i)); v[pos[2]].push_back(pii(pos[2]+1,i)); } } ll ans=0; for(int i=1;i<=n;i++) { ans+=query(1,i,n,1,sz); for(int j=0;j<v[i].size();j++) if(v[i][j].first<0) modify(1,i,-v[i][j].first,1,sz,v[i][j].second); else modify(1,v[i][j].first,n,1,sz,v[i][j].second); v[i].clear(); } printf("%lld\n",ans); } return 0; }
I. N门问题
(2020.2.5补)
计算概率的方法是,每一轮将打开的门的概率 平摊到 除了火山哥所在的 其余门上;感觉题目说的不太清楚...
其实不太会证明为什么$N>10$时概率为$0$...
并且也没有想懂题解的dp,还需要再推一下
但如果已知只需要处理$N\leq 10$的情况时,直接爆搜就可以了
有一个剪枝的办法是,对于所有火山哥视角下概率最优的门,没有奖的门都是等价的,于是只需要搜一个没有奖的门和有奖的门即可
假装这是个EXCRT模板题(

#include <cmath> #include <cstdio> #include <vector> #include <algorithm> using namespace std; typedef long long ll; const int N=105; const int M=50005; double eps=0.0000001; //解决同余方程组a_i*x=b_i(mod m_i) //在主函数依次调用 //fold(a,b,m,n)和excrt(b,m,n) //求解ax+by=gcd(a,b),返回gcd(a,b) ll exgcd(ll a,ll b,ll &x,ll &y) { if(b==0LL) { x=1,y=0; return a; } ll tmp=exgcd(b,a%b,y,x); y=y-a/b*x; return tmp; } inline ll mod(ll x,ll m) { if(x>=m) x-=m; if(x<0) x+=m; return x; } //防止中间结果爆longlong的x*y%m ll mul(ll x,ll y,ll m) { ll res=0,tmp=x; x=mod(x%m+m,m),y=mod(y%m+m,m); while(y) { if(y&1) res=mod(res+tmp,m); tmp=mod(tmp<<1,m); y>>=1; } return res; } //求解方程组x_i=a_i mod m_i ll excrt(ll *a,ll *m,int n) { ll res=0,lcm=1; for(int i=1;i<=n;i++) { ll A,B,C,x,y,gcd; A=lcm,B=m[i],C=a[i]-res; gcd=exgcd(A,B,x,y); //无解 if(C%gcd!=0) return -1; ll tmp=lcm; lcm=lcm/gcd*m[i]; res=res+mul(C/gcd,mul(tmp,x,lcm),lcm); res=mod(res%lcm+lcm,lcm); } return res; } //将a_i的逆元乘到b_i上 //之后要excrt的是b_i与m_i ll fold(ll *a,ll *b,ll *m,int n) { for(int i=1;i<=n;i++) { ll x,y,gcd; gcd=exgcd(a[i],m[i],x,y); //无逆元 if(b[i]%gcd!=0) return -1; a[i]/=gcd,b[i]/=gcd,m[i]/=gcd; exgcd(a[i],m[i],x,y); b[i]=mul(b[i],x,m[i]); } return 1; } int n; double p[N]; double dfs(int x,int pos) { if(x==n-1) return (pos==1?1.0:0.0); vector<int> v; double save[N]; for(int i=1;i<=n;i++) { save[i]=p[i]; if(p[i]>eps && i!=pos) v.push_back(i); } double res=1.0; for(int i=0;i<v.size();i++) { if(v[i]==1) continue; double rem=p[v[i]]/(v.size()-1); p[v[i]]=0.0; for(int j=0;j<v.size();j++) if(j!=i && v[j]!=pos) p[v[j]]+=rem; double maxp=*max_element(p+1,p+n+1),sum=0.0; int cnt=0; for(int j=2;j<=n;j++) if(abs(maxp-p[j])<eps) { if(!cnt) sum+=dfs(x+1,j); cnt++; } sum=sum*cnt; if(abs(maxp-p[1])<eps) sum+=dfs(x+1,1),cnt++; res=min(res,sum/cnt); for(int j=1;j<=n;j++) p[j]=save[j]; } return res; } double ans[N]; ll b[M],m[M]; int main() { for(n=2;n<=10;n++) { for(int i=1;i<=n;i++) p[i]=1.0/n; ans[n]=(dfs(1,n)*(n-1)+dfs(1,1))/n; } int T; scanf("%d",&T); for(int i=1;i<=T;i++) scanf("%lld%lld",&b[i],&m[i]); ll res=excrt(b,m,T); if(res<2) printf("error"); else printf("%.6f",res<11?ans[res]:0.0); return 0; }
J. 简单字符串
待补
Overall
| 题号 | A | B | C | D | E | F | G | H | I | J |
| 状态 | * | * | o | * | * | o | * | * |
A. Alternative Accounts
暴力的做法是对$k=1,2$特判,然后对$k=3$讨论

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=100005; int n,k,m[5]; int a[N]; int cnt[10]; int main() { scanf("%d%d",&n,&k); for(int i=1;i<=k;i++) { scanf("%d",&m[i]); for(int j=1;j<=m[i];j++) { int x; scanf("%d",&x); a[x]|=(1<<(i-1)); } } if(k==1) { printf("%d\n",m[1]); return 0; } if(k==2) { printf("%d\n",max(m[1],m[2])); return 0; } for(int i=1;i<=n;i++) cnt[a[i]]++; int ans=m[1]; int dlt=min(cnt[1],cnt[6]); ans+=cnt[6]-dlt; cnt[1]-=dlt; ans+=max(max(cnt[4]-cnt[3]-cnt[1],cnt[2]-cnt[5]-cnt[1]),0); printf("%d\n",ans); return 0; }
但队友在现场直接一个性质就做完了,即全选 人数最多的一场中 所有账号、或全选 参赛次数大于$2$ 的所有账号
比较显然的是,真正人数都不少于上面的两种取法;不过两者取max即为答案 仍需稍微推导一下
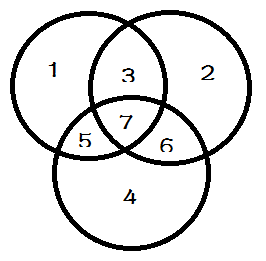
假设$1+3+5+7$是人数最大的一场,那么可以得到$1+3\geq 4+6,1+5\geq 2+6$
如果有$1>6$,那么相当于$1$足够吸收$6$的账号,并且$2$可以摊到$1,5$、$4$可以摊到$1,3$,那么显然取$1+3+5+7$是最优的
如果有$6>1$,那么足够说明$5>2,3>4$,即$2,4$已经分别为$5,3$吸收,那么只剩下$1$需要被$6$吸收,那么取$3+5+6+7$是最优的
能想到这个结论还是很强的...

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=100005; int n,m,k,sum,ans; int a[N]; int main() { scanf("%d%d",&n,&k); for(int i=1;i<=k;i++) { scanf("%d",&m); ans=max(ans,m); for(int j=1;j<=m;j++) { int x; scanf("%d",&x); a[x]++; } } for(int i=1;i<=n;i++) if(a[i]>1) sum++; printf("%d\n",max(sum,ans)); return 0; }
B. Bitset Master
看了题解豁然开朗
确实很巧妙的一题...感觉智商被碾压
考虑题目所描述的合并过程:
将$u,v$两点合并,那么合并后的集合大小为$|S_{u'}|=|S_{v'}|=|S_u|+|S_v|-|S_u\cap S_v|$
然后,$|S_u\cap S_v|$的值恰好就是 上一次利用该边合并时的$|S_u|=|S_v|$;于是可以对每条边记录这个值,合并时也同时更新边权
不过这样做出来的$S_i$是每个点集合的大小,与题目要求的不是同一个东西
如果将合并的边逆序处理,那么得到$S_i$的就是每个点权被合并进的结点数:因为当逆序合并到第$j$条边后,$S_i$表示在合并第$j\text{~}m$条边后 $i$所能到达的不同结点个数,那么合并时的转移仍是$|S_{u'}|=|S_{v'}|=|S_u|+|S_v|-|S_u\cap S_v|$
在以后遇到集合合并问题时,最好能有这道题目的意识

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; const int N=500005; int n,m; int u[N],v[N],p[N]; int val[N],last[N]; int main() { scanf("%d%d",&n,&m); for(int i=1;i<n;i++) scanf("%d%d",&u[i],&v[i]); for(int i=1;i<=m;i++) scanf("%d",&p[i]); for(int i=1;i<=n;i++) val[i]=1; for(int i=m;i>=1;i--) { int x=p[i]; val[u[x]]=val[v[x]]=last[x]=val[u[x]]+val[v[x]]-last[x]; } for(int i=1;i<=n;i++) printf("%d",val[i]),putchar(i<n?' ':'\n'); return 0; }
C. Self-Adjusting Segment Tree
(2020.2.5补)
也是十分巧妙的转化思想
看到$n=500$其实就能感觉出来是区间dp了,但是状态的转移不太直观:对于某个线段树节点,假如它被一个查询包含,那么只有该节点会对答案产生$1$的贡献,而其子节点虽然也被包含、但没有贡献;按照这个思路很难解决这个问题
不过如果对线段树的访问计数更加深入思考的话(虽然我是想不出来啦...),能够这样转化问题:
1. 如果线段树上区间$[l,r]$和查询区间$[ql,qr]$相交、且$[l,r]$不被$[ql,qr]$完全包含,则对答案产生$1$的贡献
2. 如果$[l,r]$被$[ql,qr]$完全包含 且$l\neq r$(即不是叶节点),则对答案产生$-1$的贡献
3. 如果$[l,r]$被$[ql,qr]$完全包含 且$l=r$(即是叶节点),则对答案产生$1$的贡献
1是比较显然的,因为这是定位区间过程中的贡献
而23则是将正常线段树查询时 定位到的logn级别的子区间 进行转化
正确性也是好理解的,因为对于一个长度为$k$的子区间,将其中元素两两合并得到一棵树时,一共有$k$个叶节点和$k-1$个非叶节点,则对答案一共产生$k-(k-1)=1$的贡献
这样一来,可以写出dp方程了:
$dp[i][j]=min\{dp[i][k]+dp[k+1][j]\}+w[i][j]$,其中$w[i][j]$是对于线段树上区间$[i,j]$ 上述12两种情况的贡献
初始状态是$dp[i][i]=i\text{被查询包含的数量}$,差分一下就能得到
$w[i][j]$的求法题解没讲,我的做法是固定$i$,然后对所有查询进行差分:
对于$ql\leq i$的查询,在$j\leq qr$时被包含、贡献为$-1$,在$j>qr$时相交、贡献为$1$;于是在$i$处打上$-1$、在$qr+1$处打上$+2$就行了
对于$ql>i$的查询,在$j\geq ql$时相交、贡献为$1$;在$ql$处打上$+1$即可

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=505; const int M=200005; int n,m; int ql[M],qr[M]; int tag[N]; int w[N][N],dp[N][N]; int dfs(int l,int r) { if(dp[l][r]) return dp[l][r]; dp[l][r]=dfs(l,l)+dfs(l+1,r); for(int i=l+1;i<r;i++) dp[l][r]=min(dp[l][r],dfs(l,i)+dfs(i+1,r)); return dp[l][r]+=w[l][r]; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) scanf("%d%d",&ql[i],&qr[i]); for(int i=1;i<=n;i++) { memset(tag,0,sizeof(tag)); for(int j=1;j<=m;j++) { if(ql[j]<=i && qr[j]>=i) w[i][i]--,tag[qr[j]+1]+=2; if(ql[j]>i) tag[ql[j]]++; } for(int j=i+1;j<=n;j++) w[i][j]=w[i][j-1]+tag[j]; } memset(tag,0,sizeof(tag)); for(int i=1;i<=m;i++) tag[ql[i]]++,tag[qr[i]+1]--; for(int i=1;i<=n;i++) { tag[i]=tag[i-1]+tag[i]; dp[i][i]=tag[i]; } printf("%d\n",dfs(1,n)); return 0; }
D. Circle Union
待补
E. Matching Problem
修改过的数据范围是$n\leq 300$
所以可以$n^3$枚举前$3$位,然后最后一位$O(1)$check一下
写的不够优美...应该有更好的写法

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=305; int n; int a[N]; int b[5],last[5]; int val[5],rem[N][N],vis[N]; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]); for(int i=1;i<=4;i++) { scanf("%d",&b[i]); for(int j=i-1;!last[i] && j>=1;j--) if(b[i]==b[j]) last[i]=j; } for(int i=n;i>=1;i--) { for(int j=1;j<=n;j++) rem[i][j]=rem[i+1][j]; rem[i][a[i]]++; } ll ans=0; for(int i=1;i<=n;--vis[a[i]],i++) { val[1]=a[i],vis[a[i]]++; for(int j=i+1;j<=n;--vis[a[j]],j++) { val[2]=a[j],vis[a[j]]++; if(!last[2] && vis[a[j]]>1) continue; if(last[2] && val[2]!=val[last[2]]) continue; for(int k=j+1;k<=n;--vis[a[k]],k++) { val[3]=a[k],vis[a[k]]++; if(!last[3] && vis[a[k]]>1) continue; if(last[3] && val[3]!=val[last[3]]) continue; if(last[4]) ans+=rem[k+1][val[last[4]]]; else { ans+=n-k; for(int l=1;l<4;l++) if(!last[l]) ans-=rem[k+1][val[l]]; } } } } printf("%lld\n",ans); return 0; }
F. Inversion Pairs
待补
G. Cryptographically Secure Pseudorandom Number Generator
并不是很懂$q<=10^{16}$应该怎么做...等着学习一下标程
本来也想到了差不多在$\sqrt{q}$左右meet in the middle,不过由于快速幂求逆元带log,于是永远TLE
后来搜到一个$O(n)$递推求逆元的式子,参考:减维 - 【乘法逆元】简单说说乘法逆元的求法
rev[1]=1; for(int i=2;i<=n;i++) rev[i]=(P-P/i)*rev[P%i]%P;
这样就直接顺序枚举,直到$i==min\{rev(j),j<i\}$结束

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; typedef pair<ll,ll> pii; ll P; ll rev[1000005]; vector<pii> v; int main() { int T; scanf("%d",&T); while(T--) { v.clear(); scanf("%lld",&P); rev[1]=1; ll minv=1LL<<30; for(int i=2;i<min(minv,P);i++) { rev[i]=(P-P/i)*rev[P%i]%P; if(rev[i]<minv) { v.push_back(pii(i,rev[i])); minv=rev[i]; } } int flag=(v.size() && v.back().first==v.back().second); printf("%d\n",(int)v.size()*2-flag); for(int i=0;i<v.size();i++) printf("%lld %lld\n",v[i].first,v[i].second); for(int i=(int)v.size()-1-flag;i>=0;i--) printf("%lld %lld\n",v[i].second,v[i].first); } return 0; }
H. Geometry PTSD
(2020.2.7补)
这题主要的工作是写checker
$V=\frac{1}{3}Sh$,分别求出$V$和$S$就能得出$h$了
$V$可以用三阶行列式计算,空间三角形的$S$用海伦公式比较方便
具体公式注释在代码前面

#include <cmath> #include <cstdio> #include <cstdlib> #include <iomanip> #include <iostream> #include <algorithm> using namespace std; typedef long double db; const int N=105; const db eps=1e-19; const db lim=1e-18; //求面积:1/2 * | x1-x0 y1-y0 | // | x2-x0 y2-y0 | //求面积(海伦公式):三边为a, b, c p=1/2(a+b+c) // S = sqrt(p*(p-a)*(p-b)*(p-c)) //求体积:1/6 * | x1-x0 y1-y0 z1-z0 | // | x2-x0 y2-y0 z2-z0 | // | x3-x0 y3-y0 z3-z0 | //求点到面距离:d=3V/S 即两行列式相除 struct Determinant { db a[N][N]; Determinant() { for(int i=0;i<N;i++) for(int j=0;j<N;j++) a[i][j]=0.0; } db calc(int n) { for(int i=0;i<n;i++) { int maxp=-1; db maxv=eps; for(int j=i;j<n;j++) if(abs(a[j][i])>maxv) maxv=abs(a[j][i]),maxp=j; if(maxp<0) return 0.0; for(int j=0;j<n;j++) swap(a[i][j],a[maxp][j]); for(int j=i+1;j<n;j++) { db mul=a[j][i]/a[i][i]; for(int k=i;k<n;k++) a[j][k]-=mul*a[i][k]; } } db res=a[0][0]; for(int i=1;i<n;i++) res=res*a[i][i]; return res; } }M; int x[3],y[3],z[3]; db dist() { db a[3][3]; for(int i=0;i<3;i++) { db div=sqrt(1.0*x[i]*x[i]+1.0*y[i]*y[i]+1.0*z[i]*z[i]); a[i][0]=x[i]/div; a[i][1]=y[i]/div; a[i][2]=z[i]/div; } db L1=sqrt(pow(a[0][0]-a[1][0],2)+pow(a[0][1]-a[1][1],2)+pow(a[0][2]-a[1][2],2)); db L2=sqrt(pow(a[0][0]-a[2][0],2)+pow(a[0][1]-a[2][1],2)+pow(a[0][2]-a[2][2],2)); db L3=sqrt(pow(a[1][0]-a[2][0],2)+pow(a[1][1]-a[2][1],2)+pow(a[1][2]-a[2][2],2)); db P=(L1+L2+L3)/2; db area=sqrt(P*(P-L1)*(P-L2)*(P-L3)); for(int i=0;i<3;i++) for(int j=0;j<3;j++) M.a[i][j]=a[i][j]; db volumn=M.calc(3)/6.0; return 3.0*volumn/area; } int main() { for(x[0]=1000000;x[0]>=999990;x[0]--) for(x[1]=-1000000;x[1]<=-999990;x[1]++) for(x[2]=-2;x[2]<=2;x[2]++) for(y[0]=1000000;y[0]>=999990;y[0]--) for(y[1]=-2;y[1]<=2;y[1]++) for(y[2]=-1000000;y[2]<=-999990;y[2]++) for(z[0]=-2;z[0]<=2;z[0]++) for(z[1]=1000000;z[1]>=999990;z[1]--) for(z[2]=-1000000;z[2]<=-999990;z[2]++) if(abs(dist())<lim && abs(dist())>eps) { for(int i=0;i<3;i++) printf("%d %d %d\n",x[i],y[i],z[i]); cout<<fixed<<setprecision(20)<<abs(dist())<<'\n'; return 0; } return 0; }
I. Practice for KD Tree
依然很想学习标程,$n=10^6$也太猛了...
应该是现场唯一一个用KD树过的?树套树做法待补
经过几次题目的测试,大概感觉是 带最优性剪枝的KD树 运行时间是BIT套线段树的$2$倍
不过KD树不太需要在意空间(一般是$O(10n)$级别的)
由于子矩阵加和子矩阵求max是分离的,而矩阵大小$n^2$并不是很大,于是可以考虑对子矩阵加差分,等到所有加操作结束后$O(n^2)$扫一遍得到现有的矩阵
接着就是很经典的子矩阵求max/min/sum这类问题了,模板题

#include <cstdio> #include <locale> #include <vector> #include <cstring> #include <algorithm> using namespace std; inline void read(int &x) { x=0; int rev=1; char ch=getchar(); while(!isdigit(ch)) ch=getchar(); if(ch=='-') rev=-1,ch=getchar(); while(isdigit(ch)) x=x*10+ch-'0',ch=getchar(); x*=rev; } inline void out(long long x) { if(x==0) { putchar('0'); return; } int len=0; static char buff[20]; while(x) buff[++len]=x%10+'0',x/=10; while(len) putchar(buff[len--]); } typedef long long ll; const int N=4000005; const int M=2005; const int DIM=2; inline int nxt(int x) { if(++x==DIM) x=0; return x; } int now; struct Node { int p[DIM]; int lb[DIM],rb[DIM]; ll val,maxv; Node(int x=0,int y=0,ll z=0) { val=maxv=z; p[0]=x,p[1]=y; } }; inline bool operator <(const Node &X,const Node &Y) { int i=now; if(X.p[i]!=Y.p[i]) return X.p[i]<Y.p[i]; for(int i=nxt(now);i!=now;i=nxt(i)) if(X.p[i]!=Y.p[i]) return X.p[i]<Y.p[i]; return false; } inline bool operator ==(const Node &X,const Node &Y) { for(int i=0;i<DIM;i++) if(X.p[i]!=Y.p[i]) return false; return true; } int root; struct KDTree { Node cur,t[N]; int ls[N],rs[N]; inline void newnode(int x) { ls[x]=rs[x]=0; t[x].val=cur.val; t[x].maxv=cur.maxv; for(int i=0;i<DIM;i++) t[x].lb[i]=t[x].rb[i]=t[x].p[i]=cur.p[i]; } void pushup(int x) { if(ls[x]) for(int i=0;i<DIM;i++) { t[x].lb[i]=min(t[x].lb[i],t[ls[x]].lb[i]); t[x].rb[i]=max(t[x].rb[i],t[ls[x]].rb[i]); } if(rs[x]) for(int i=0;i<DIM;i++) { t[x].lb[i]=min(t[x].lb[i],t[rs[x]].lb[i]); t[x].rb[i]=max(t[x].rb[i],t[rs[x]].rb[i]); } } void build(int &x,int l,int r,int type) { x=(l+r)>>1; now=type; nth_element(t+l,t+x,t+r+1); cur=t[x]; newnode(x); if(l<x) build(ls[x],l,x-1,nxt(type)); if(x<r) build(rs[x],x+1,r,nxt(type)); pushup(x); update(x); } void update(int x) { t[x].maxv=t[x].val; if(ls[x]) t[x].maxv=max(t[x].maxv,t[ls[x]].maxv); if(rs[x]) t[x].maxv=max(t[x].maxv,t[rs[x]].maxv); } void query(int x,ll &ans) { if(t[x].maxv<=ans) return; if(t[x].rb[0]<cur.lb[0] || t[x].lb[0]>cur.rb[0]) return; if(t[x].rb[1]<cur.lb[1] || t[x].lb[1]>cur.rb[1]) return; if(t[x].lb[0]>=cur.lb[0] && t[x].rb[0]<=cur.rb[0] && t[x].lb[1]>=cur.lb[1] && t[x].rb[1]<=cur.rb[1]) { ans=max(ans,t[x].maxv); return; } if(t[x].p[0]>=cur.lb[0] && t[x].p[0]<=cur.rb[0] && t[x].p[1]>=cur.lb[1] && t[x].p[1]<=cur.rb[1]) ans=max(ans,t[x].val); int L=ls[x],R=rs[x]; if(t[L].maxv<t[R].maxv) swap(L,R); if(L) query(L,ans); if(R) query(R,ans); } }tree; int n,m1,m2; ll a[M][M]; int main() { read(n),read(m1),read(m2); tree.build(root,1,n*n,0); for(int i=1;i<=m1;i++) { int x1,y1,x2,y2,w; read(x1),read(y1),read(x2),read(y2),read(w); a[x2][y2]+=w; a[x1-1][y2]-=w; a[x2][y1-1]-=w; a[x1-1][y1-1]+=w; } for(int i=2*n;i>=1;i--) { for(int j=min(n,i-1);j>=max(1,i-n);j--) { int y=j,x=i-j; a[x][y]+=a[x+1][y]+a[x][y+1]-a[x+1][y+1]; tree.t[(x-1)*n+y]=Node(x,y,a[x][y]); } } tree.build(root,1,n*n,0); for(int i=1;i<=m2;i++) { int x1,y1,x2,y2; read(x1),read(y1),read(x2),read(y2); tree.cur.lb[0]=x1,tree.cur.rb[0]=x2; tree.cur.lb[1]=y1,tree.cur.rb[1]=y2; ll ans=0; tree.query(root,ans); out(ans),putchar('\n'); } return 0; }
J. Xor on Figures
又是智商被碾压的一题...
这题现场看到01染色就走上了Polya的不归路,还是见识不够
一共有$2^{2k}$种翻转方式(以每一格为pattern的左上角),并且每种翻转方式相当于一个长度为$2^{2k}$的01串
若将其做成一个$2^{2k}\times 2^{2k}$的矩阵,并进行高斯消元
那么,所有本质不同的翻转方式种数,就是该矩阵的秩
道理很简单:如果某种翻转可以由其他几种方式合成而来,那么在已选那几种方式之后,当前的翻转方式对于最终的“不同”答案数是没有贡献的
于是答案为$2^{rank(M)}$
普通高斯消元的复杂度是$O(2^{6k})$;不过在确定主元后,对于每一行的消去仅为xor,所以可以考虑用bitset加速;最终复杂度为$O(2^{6k}/w)$

#include <cstdio> #include <bitset> #include <cstdlib> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const ll MOD=1000000007; const int N=1030; int n; char s[N][N]; bitset<N> bs[N]; inline int mod(int x) { if(x>=n) x-=n; return x; } int gauss() { int m=n*n,rank=0; for(int i=0;i<m;i++) { int j=rank; while(j<m && bs[j][i]==0) j++; if(j==m) continue; if(rank!=j) swap(bs[rank],bs[j]); for(j=rank+1;j<m;j++) if(bs[j][i]==1) bs[j]^=bs[rank]; rank++; } return rank; } inline ll quickpow(ll x,int k) { ll res=1; while(k) { if(k&1) res=res*x%MOD; x=x*x%MOD; k>>=1; } return res; } int main() { scanf("%d",&n); n=1<<n; for(int i=0;i<n;i++) scanf("%s",s[i]); for(int i=0;i<n;i++) for(int j=0;j<n;j++) { int pos=i*n+j; for(int k=0;k<n;k++) for(int l=0;l<n;l++) bs[pos][k*n+l]=(s[mod(k+i)][mod(l+j)]=='1'?1:0); } int rank=gauss(); printf("%lld\n",quickpow(2LL,rank)); return 0; }
Overall
| 题号 | A | B | C | D | E | F | G | H | I | J | K | L | M | N |
| 状态 | * | o | * | * | * | * | * | * | * | * | * |
A. Convolution
待补,等一个NTT板子
B. 双圈覆盖
待补
C. 酒馆战棋
要看清“从左到右依次攻击”
求最大时尽量我方普通撞对方圣盾;求最小时尽量我方剧毒撞对方圣盾

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=1005; int n,A,B,C,D; char s[N]; int main() { int T; scanf("%d",&T); while(T--) { scanf("%d%d%d%d%d",&n,&A,&B,&C,&D); scanf("%s",s); int a=A,b=B,c=C,d=D; int maxans=0,minans=0; for(int i=0;i<n;i++) if(s[i]=='1') { if(c) { maxans++,c--; continue; } if(d) { d--,c++; continue; } if(a) { maxans++,a--; continue; } if(b) b--,a++; } else { if(d) { d--,c++; continue; } if(c) continue; if(b) b--,a++; } a=A,b=B,c=C,d=D; for(int i=0;i<n;i++) if(s[i]=='1') { if(d) { d--,c++; continue; } if(c) { minans++,c--; continue; } if(b) { b--,a++; continue; } if(a) minans++,a--; } else { if(c) continue; if(d) { d--,c++; continue; } if(a) continue; if(b) b--,a++; } printf("%d %d\n",maxans,minans); } return 0; }
D. 递增递增
待补
E. Access
(2020.2.7补)
这题可以看出是一个树上背包,不过状态的转移很需要思考,以及需要对于这种转移正确估计复杂度
用$dp[i][j]$表示,在$i$的子树中Access $j$次的不同方案数
不过这个方案数是只仅考虑边的虚实情况,且对于$i$的第一次Access需要特判(即,子树中仅Access $i$)
因为比如这样的一个图
$3\ 2\\1\ 2\\1\ 3$
如果Access $2$再Acess $1$,那么$2$次Access的结果就是一个全虚边的树,会重复计数
所以这道题中的处理方法是将这类Access放到$fa[i]$进行转移
记考虑$x$的子树内的方案数,$son_x$为$x$的儿子们,那么一共分为$3$种转移方式:
1. 正常转移,即对于$x$进行背包
不过那么在dp的过程中,就需要引入两个$500\times 2$的中间数组$res[i][j],tmp[i][j]$,表示总Access次数为$i$、是否已将某个$son_x$的边作为$x$的儿子这一层的唯一实边的当前方案数;若仅用一个数组,那么背包的过程中会被当前的$son_x$影响多次、产生错误,所以用$res$记录 考虑$son_x$之前儿子的方案,用$tmp$记录 用$son_x$进行转移的方案;在一遍转移后,再将$tmp$赋给$res$
于是有这样的转移方程:$tmp[i+j][0]=tmp[i+j][0]+res[i][0]\cdot dp[son_x][j]\text{(son_x不为实边)}\\ tmp[i+j][1]=tmp[i+j][1]+res[i][0]\cdot dp[j][0]\text{(son_x为实边,要求j>0)}\\ tmp[i+j][1]=tmp[i+j][1]+res[i][1]\cdot dp[j][0]\text{(son_x不为实边)}$
2. 上面所说的,选择$son_x$为其子树内唯一Access的节点
那么其必为实边,否则跟不Access $son_x$是一样的方案
于是转移方程为:$tmp[i][1]=tmp[i][1]+res[i][0]$
对于所有的$son_x$都做完背包后,$dp[x][i]=res[i][1]$
3. 对$x$进行Access(且$x$不为唯一Access的节点)
那么此时就相当于$x$的儿子这一层一条实边也没有,于是有$dp[x][i+1]=dp[x][i+1]+res[i][0],i\geq 1$
这样就能得到最终答案了
然后在这种$dp$中,看似对于每一个儿子要进行双重for循环,有点$O(nk^2)$的意思
不过实际上,每个循环的上界都与子树大小有关;若加上这一个限制,整个方程就是$O(nk)$的
因为,对于极端情况(菊花树),设子树大小都为$sz(sz<<k)$,那么对于根节点计算的时间复杂度为$k\cdot sz\cdot \frac{n}{sz}=kn$,而其余子树的复杂度很低;对于另一种极端情况(长链),主干上每次伸出几个大小为$k$的子树,那么这样的分支点不超过$\frac{n}{k}$个,均摊下来依然是$k^2\cdot \frac{n}{k}=nk$
还需要多接触点树上问题啊...

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; const int MOD=998244353; const int N=10005; const int K=505; int n,k; vector<int> v[N]; int fa[N]; int tot,ord[N]; int sz[N]; int dp[N][K]; int res[K][2],tmp[K][2]; void solve(int x) { memset(res,0,sizeof(res)); sz[x]=1; res[0][0]=1; for(int it=0;it<v[x].size();it++) { int nxt=v[x][it]; if(nxt==fa[x]) continue; memset(tmp,0,sizeof(tmp)); //正常的三种转移 for(int i=0;i<=min(sz[x]-1,k);i++) for(int j=0;j<=min(sz[nxt]-1,k-i);j++) { tmp[i+j][0]=(tmp[i+j][0]+1LL*res[i][0]*dp[nxt][j])%MOD; if(j) tmp[i+j][1]=(tmp[i+j][1]+1LL*res[i][0]*dp[nxt][j])%MOD; tmp[i+j][1]=(tmp[i+j][1]+1LL*res[i][1]*dp[nxt][j])%MOD; } sz[x]+=sz[nxt]; //仅取nxt for(int i=1;i<=k;i++) tmp[i][1]=(tmp[i][1]+res[i-1][0])%MOD; //覆盖回去 for(int i=0;i<=k;i++) for(int j=0;j<2;j++) res[i][j]=tmp[i][j]; } dp[x][0]=1; for(int i=1;i<=k;i++) { dp[x][i]=(dp[x][i]+res[i][1])%MOD; //取x if(i) dp[x][i+1]=(dp[x][i+1]+res[i][0])%MOD; } } int main() { scanf("%d%d",&n,&k); for(int i=1;i<n;i++) { int x,y; scanf("%d%d",&x,&y); v[x].push_back(y); v[y].push_back(x); } ord[++tot]=1; for(int i=1;i<=tot;i++) for(int x=ord[i],j=0;j<v[x].size();j++) { int nxt=v[x][j]; if(nxt!=fa[x]) fa[nxt]=x,ord[++tot]=nxt; } for(int i=tot;i>=1;i--) solve(ord[i]); int ans=0; for(int i=0;i<=k;i++) ans=(ans+dp[1][i])%MOD; printf("%d\n",ans); return 0; }
F. 图与三角形
场上卡了好久,甚至开始分析起边的生成规律了...说明思路不开阔
正面考虑这个问题比较困难,不过如果考虑三边不全同色的三角形则简单很多
这样的三角形必定为 白白黑 或 黑黑白,那么如果记录每个顶点的白边、黑边数量,则可以表示为$\frac{1}{2}\sum_{i=1}^{n} (white_i\cdot black_i)$
用总数$C_n^3$减去该值就行了

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=5005; int n; int A,B,C,P,D; int white[N],black[N]; int main() { scanf("%d",&n); scanf("%d%d%d%d%d",&A,&B,&C,&P,&D); for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) if((1LL*A*(i+j)*(i+j)+1LL*B*(i-j)*(i-j)+C)%P>D) black[i]++,black[j]++; else white[i]++,white[j]++; ll ans=0; for(int i=1;i<=n;i++) ans+=white[i]*black[i]; printf("%lld\n",1LL*n*(n-1)*(n-2)/6-ans/2); return 0; }
G. 单调栈
首先,如果一个序列$f$中有多个$1$,那么显然需要从最后一个$1$的位置向前在$p$中填$1,2,3,...$(否则不满足题目中所描述的性质)
所以,对于在序列$f$中多次出现的数在$p$中对应位置的填数方式就是确定的了,即从最靠后位置向前填数依次递增(并且此填数方法得到的$p$字典序最小)
然后考虑最小的序列$p$,即$1,2,3,...,n$,其对应的$f$为$1,2,3,...,n$
如果我们调整$f$为$1,2,2,4,5,...,n$,那么最小的序列$p$为$1,3,2,4,5,...,n$
于是可以产生一种直觉:如果$f$中有$-1$,那么把它尽量往大填时,还原出来的$p$字典序更小
打表检验了一下发现的确是这样,于是就直接搞了
(严格的证明待补)

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=105; int n; int f[N]; int a[N]; int main() { int T; scanf("%d",&T); while(T--) { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&f[i]); int maxv=0; for(int i=1;i<=n;i++) { if(f[i]<0) f[i]=min(i,maxv+1); maxv=max(f[i],maxv); } int cnt=0; for(int i=1;i<=n;i++) for(int j=n;j>=1;j--) if(f[j]==i) a[j]=++cnt; for(int i=1;i<=n;i++) printf("%d",a[i]),putchar(i==n?'\n':' '); } return 0; }
H. 异或询问
在一个小bug卡了三个小时,智商感人...
下次在跳过一段重复的数时,一定要让$i=j+1$而不是$i++$!!
这道题有个很奇妙的性质,就是$i\ xor\ x,l\leq i\leq r$会被分成log级别的连续区间
可以从一个较简单的情况考虑,即令$l=0$:
假设当前某段连续区间为$[l',r']$,若$l',r'$在某一二进制位不同,且$x$在该位为$1$,那么相当于将该位为$0$的区间翻转到该位为$1$,反之亦然;若相同则向后一位判断
这就类似于在线段树上查找一个区间时,会定位到log个子区间上;只不过在这里这些子区间不连续
于是对于每次询问的$l,r,x$,可以对$\sum_{i=0}^{l-1}f(i\ xor\ x)^2,\sum_{i=0}^{r}f(i\ xor\ x)^2$分别计算
想要计算每一次询问所拆出的log个区间,需要对$a$数组进行预处理、得到$f(i)^2$的前缀和:这可以通过sort $a$后对$a_i$事先计算、查询时二分做到
于是总体复杂度是$O(q\cdot (logn)^2)$

#include <cstdio> #include <vector> #include <algorithm> using namespace std; typedef pair<int,int> pii; typedef long long ll; const int N=100005; const ll MOD=998244353; int n,Q; int a[N]; vector<pii> seg; void split(int l,int r,int x,int bit) { if(r-l+1==(1<<(bit+1))) { x=(x>>(bit+1))<<(bit+1); l^=x,r^=x; if(l>r) swap(l,r); seg.push_back(pii(l,r)); return; } int mid=((l>>bit)+1)<<bit; if(r>=mid) { split(l,mid-1,x,bit-1); split(mid,r,x,bit-1); } else split(l,r,x,bit-1); } ll sum[N]; inline ll calc(int x) { if(x<0) return 0; int pos=upper_bound(a,a+n+1,x)-a; if(a[pos]>x) pos--; return (sum[pos]+1LL*(x-a[pos]+1)*pos%MOD*pos%MOD)%MOD; } inline ll calc(int l,int r) { return (calc(r)-calc(l-1)+2*MOD)%MOD; } int main() { scanf("%d%d",&n,&Q); for(int i=1;i<=n;i++) scanf("%d",&a[i]); a[n+1]=1<<30; sort(a+1,a+n+1); for(int i=1;i<=n;) { int j=i; while(j+1<=n && a[j+1]==a[i]) j++; sum[j]=(sum[i-1]+1LL*(a[j]-a[i-1])*(i-1)%MOD*(i-1))%MOD; i=j+1; } while(Q--) { ll ans=0; int l,r,x; scanf("%d%d%d",&l,&r,&x); seg.clear(); if(l-1>=0) split(0,l-1,x,29); for(int i=0;i<seg.size();i++) ans=(ans-calc(seg[i].first,seg[i].second)+MOD)%MOD; seg.clear(); split(0,r,x,29); for(int i=0;i<seg.size();i++) ans=(ans+calc(seg[i].first,seg[i].second))%MOD; printf("%lld\n",ans); } return 0; }
I. 变大!
场上虽然想到了dp,但是状态复杂很多...说明对问题的性质认识不足
考虑一段一段地将某段区间刷成该区间中的最大值
不论该区间长度是奇数还是偶数、最大值的位置在哪里,所需要的操作次数都是$\frac{len}{2}$(因为每操作一次能保证改变$2$个位置)
于是考虑$dp[i][j]$表示,当前区间的起点为$i$、之前已经操作了$j$次
那么可以写出转移的式子$dp[i'][j+(i'-i)/2]=max(dp[i'][j+(i'-i)/2],dp[i][j]+max_{k=i}^{i'-1} a_k\cdot (i'-i))$和$dp[i+1][j]=max(dp[i+1][j],dp[i][j]+a[i])$
总体是$n^2$的状态和$n$的转移

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=55; int n; int a[N]; int maxv[N][N]; int dp[N][N]; int main() { int T; scanf("%d",&T); while(T--) { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]); memset(maxv,0,sizeof(maxv)); for(int i=1;i<=n;i++) for(int j=i;j<=n;j++) maxv[i][j]=max(a[j],maxv[i][j-1]); memset(dp,-1,sizeof(dp)); dp[1][0]=0; for(int i=1;i<=n;i++) { for(int j=0;j<=n/2;j++) { if(dp[i][j]<0) continue; dp[i+1][j]=max(dp[i+1][j],dp[i][j]+a[i]); for(int k=i+2;k<=n+1;k++) dp[k][j+(k-i)/2]=max(dp[k][j+(k-i)/2], dp[i][j]+maxv[i][k-1]*(k-i)); } } for(int i=1;i<=n/2;i++) printf("%d",dp[n+1][i]),putchar(i==n?'\n':' '); for(int i=n/2+1;i<=n;i++) printf("%d",maxv[1][n]*n),putchar(i==n?'\n':' '); } return 0; }
J. K重排列
对于一个序列$p$,可以将$i$与$p_i$连一条边,这样每个环内都各自构成一个循环
那么能够成为该序列的 周期的$K$必须为所有环长的lcm的倍数
考虑对环长的所有情况进行枚举,那么就是$n$的一个整数划分;在$n=50$时数量较小,可以dfs
在dfs的过程中,可以按照环长递减的顺序进行枚举;按这个顺序可以不枚举环长为$1$的情况,而直接在回溯时加
对于$dfs(x,low,num)$,$x$表示剩余数量,$low$表示上次枚举的环长,$num$表示环长与上次相同的环的总数
那么可以向$dfs(x-low,low,num+1)$和$dfs(x-j,j,1)$转移
一个长度为$i$的环,满足条件的排列有$(i-1)!$个(通过找规律可以看出,不太会证)
于是对于第二种转移,该步贡献的乘数为$C_x^j\cdot (j-1)!$
对于第一种转移,由于所有长度相同的环是等价的,于是要除以$num+1$(其实是将$(num+1)!$摊到每一步),即贡献了$C_x^{low}\cdot (low-1)!\cdot \frac{1}{num+1}$

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=55; const int MOD=998244353; ll fac[N],rev[N]; ll C[N][N]; int n; ll K,ans; ll gcd(ll a,ll b) { if(b==0) return a; return gcd(b,a%b); } void dfs(int x,int low,int num,ll lcm,ll val) { if(K%lcm) return; for(int i=min(low,x);i>=2;i--) { int nnum=(i==low?num+1:1); dfs(x-i,i,nnum,lcm*i/gcd(lcm,i),val*C[x][i]%MOD*fac[i-1]%MOD*rev[nnum]%MOD); } ans=(ans+val)%MOD; } int main() { fac[0]=fac[1]=1,rev[1]=1; for(int i=2;i<=50;i++) fac[i]=fac[i-1]*i%MOD,rev[i]=(MOD-MOD/i)*rev[MOD%i]%MOD; for(int i=0;i<=50;i++) C[i][0]=C[i][i]=1; for(int i=1;i<=50;i++) for(int j=1;j<i;j++) C[i][j]=(C[i-1][j]+C[i-1][j-1])%MOD; int T; scanf("%d",&T); while(T--) { ans=0; scanf("%d%lld",&n,&K); dfs(n,n,0,1,1); printf("%lld\n",ans); } return 0; }
K. 最大权值排列
越靠中间越大即可;因为越靠中间,被包含的区间数越多,则对答案的贡献越多

#include <cstdio> using namespace std; const int N=100005; int n; int a[N]; int main() { scanf("%d",&n); for(int i=1;i<=(n+1)/2;i++) a[i]=i*2-1; for(int i=1;i<=n/2;i++) a[n-i+1]=i*2; for(int i=1;i<=n;i++) printf("%d",a[i]),putchar(i<n?' ':'\n'); return 0; }
L. 你吓到我的马了.jpg
签到

#include <queue> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef pair<int,int> pii; const int N=105; const int dx[4]={-1,1,0,0},dy[4]={0,0,-1,1}; const int ddx[4][2]={{-1,-1},{1,1},{-1,1},{-1,1}}, ddy[4][2]={{-1,1},{-1,1},{-1,-1},{1,1}}; int n,m; char a[N][N]; inline bool inBoard(int x,int y) { return (x>=1 && x<=n && y>=1 && y<=m); } queue<pii> Q; int dist[N][N]; int main() { memset(dist,-1,sizeof(dist)); scanf("%d%d",&n,&m); int sx,sy; for(int i=1;i<=n;i++) { scanf("%s",a[i]+1); for(int j=1;j<=m;j++) if(a[i][j]=='M') sx=i,sy=j; } Q.push(pii(sx,sy)); dist[sx][sy]=0; while(!Q.empty()) { int x=Q.front().first,y=Q.front().second; Q.pop(); for(int i=0;i<4;i++) { int nx=x+dx[i],ny=y+dy[i]; if(!inBoard(nx,ny) || a[nx][ny]=='X') continue; for(int j=0;j<2;j++) { int nnx=nx+ddx[i][j],nny=ny+ddy[i][j]; if(!inBoard(nnx,nny) || a[nnx][nny]=='X') continue; if(dist[nnx][nny]<0) { dist[nnx][nny]=dist[x][y]+1; Q.push(pii(nnx,nny)); } } } } for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) printf("%d",dist[i][j]),putchar(j<m?' ':'\n'); return 0; }
M. 自闭
签到

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; const int N=105; const int M=15; int n,m,W; vector<int> v[N][M]; int cnt[M]; bool vis[N]; int ans[N]; int main() { scanf("%d%d%d",&n,&m,&W); while(W--) { int x,y,c; scanf("%d%d%d",&x,&y,&c); v[x][y].push_back(c); } for(int i=1;i<=n;i++) { int att=0,ac=0,ak=1; for(int j=1;j<=m;j++) { bool flag=false; for(int k=0;k<v[i][j].size();k++) if(v[i][j][k]==1) flag=true; if(flag) { cnt[j]++; ac++; } else ak=0; att+=(int)v[i][j].size(); } if(att==0) { vis[i]=true; ans[i]=998244353; } else if(ac==0) { vis[i]=true; ans[i]=1000000; } if(ak==1) { vis[i]=true; ans[i]=0; } } for(int i=1;i<=n;i++) { if(vis[i]) continue; for(int j=1;j<=m;j++) { bool flag=false; int maxwa=0,curwa=0; for(int k=0;k<v[i][j].size();k++) { if(v[i][j][k]==1) flag=true,curwa=0; else { ++curwa; maxwa=max(maxwa,curwa); } } if(cnt[j]>0 && !flag) ans[i]+=20; if(cnt[j]>=n/2 && !flag) ans[i]+=10; ans[i]+=maxwa*maxwa; if(!flag) ans[i]+=maxwa*maxwa; } } for(int i=1;i<=n;i++) printf("%d\n",ans[i]); return 0; }
N. 合并!
不说结论有点想不到?$n=2000$有点迷惑
答案$=\frac{1}{2}\sum_{i=1}^{n}(a_i(\sum_{j=1}^{n}a_j -a_i))$,因为每一对$a_ia_j$都恰好出现一次

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=2005; int n; ll a[N],sum,ans; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%lld",&a[i]),sum+=a[i]; for(int i=1;i<=n;i++) ans+=(sum-a[i])*a[i]; printf("%lld\n",ans/2); return 0; }
Overall
| 题号 | A | B | C | D | E | F | G | H | I | J | K | L |
| 状态 | * | * | * | * | * | * |
A. 序列
这道题还是有点东西的,相当于把暴力时$O(n^3)$的压成$O(n\cdot logn)$
考虑每一个数对$a_i,a_j$(这里是值的数对;不妨令$a_i<a_j$),它能对$(a_i,a_j)$间的所有数产生$2^{(n-j)+(i-1)}$的贡献($a_1,...,a_{i-1}$、$a_{j+1},...,a_n$可以任选)
于是考虑维护当前所有可用的数对(不过在BIT中存的是位置,因为求贡献必须知道位置的信息)
假设当前$k=i$,那么需要删去$(1,i),...,(i-1,i)$这些数对的贡献,此时的答案就是$k=i$时的得分和;再加上$(i,i+1),...,(i,n)$这些数对的贡献
比如前几项:
$i=1$:
$-$
$+\ (1,2)\ (1,3)\ ...\ (1,n)$
$i=2$:
$-\ (1,2)$
$+\ (2,3)\ (2,4)\ ...\ (2,n)$
$i=3$:
$-\ (1,3)\ (2,3)$
$+\ (3,4)\ (3,5)\ ...\ (3,n)$
可以发现,加入和删除的数对都有一端是$i$,且只加入右端大于$i$、删除左端小于$i$的数对,这方便了我们的操作
考虑$i$在$a$数组中的位置$pos[i]$,对于$j<i$和$j>i$的所有$a_j$,对答案的贡献是不一样的:前者是$2^{j-1}\cdot 2^{n-pos[i]}$,后者是$2^{pos[i]-1}\cdot 2^{n-j}$
于是需要我们分别维护所有可用右端点的权值(用来加入数对)和所有不可用左端点的权值(用来删除数对);而权值有两种,包括向左的权值$2^{j-1}$和向右的权值$2^{n-j}$
初始时,所有$i$都在可用右端点中,不可用左端点为空
对于$k=i$,我们需要对$ans$减去 (所有不可用左端点中 位置在$[1,pos[i]]$间的 向左的权值和)$\times$ $2^{n-pos[i]}$;再减去(所有不可用左端点中 位置在$[pos[i],n]$间的 向右的权值和)$\times$ $2^{pos[i]-1}$
输出答案后,我们需要对$ans$加上 (所有可用右端点中 位置在$[1,pos[i]]$间的 向左的权值和)$\times$ $2^{n-pos[i]}$;再加上(所有可用右端点中 位置在$[pos[i],n]$间的 向左的权值和)$\times$ $2^{n-pos[i]}$;最后将$i$从可用右端点中删除,加入不可用左端点中

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=100005; const int MOD=1000000007; inline int mod(int x) { if(x>=MOD) x-=MOD; if(x<0) x+=MOD; return x; } inline int lowbit(int x) { return x&(-x); } inline void Add(int *t,int k,int x) { for(int i=k;i<N;i+=lowbit(i)) t[i]=mod(t[i]+x); } inline int Query(int *t,int k) { int res=0; for(int i=k;i;i-=lowbit(i)) res=mod(res+t[i]); return res; } inline int Query(int *t,int l,int r) { return mod(Query(t,r)-Query(t,l-1)); } int pw[N]; int n; int a[N],pos[N]; //0:向左 1:向右 int add[2][N],del[2][N]; int main() { pw[0]=1; for(int i=1;i<N;i++) pw[i]=mod(pw[i-1]<<1); scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]),pos[a[i]]=i; for(int i=1;i<=n;i++) { Add(add[0],i,pw[i-1]); Add(add[1],i,pw[n-i]); } ll ans=0; for(int i=1;i<=n;i++) { ans=mod(ans-1LL*Query(del[0],1,pos[i])*pw[n-pos[i]]%MOD); ans=mod(ans-1LL*Query(del[1],pos[i],n)*pw[pos[i]-1]%MOD); printf("%lld\n",ans); Add(add[0],pos[i],-pw[pos[i]-1]); Add(add[1],pos[i],-pw[n-pos[i]]); Add(del[0],pos[i],pw[pos[i]-1]); Add(del[1],pos[i],pw[n-pos[i]]); ans=mod(ans+1LL*Query(add[0],1,pos[i])*pw[n-pos[i]]%MOD); ans=mod(ans+1LL*Query(add[1],pos[i],n)*pw[pos[i]-1]%MOD); } return 0; }
B. 四边形不等式
待补
C. 10^5万
待补
D. 方阵的行列式
待补
E. 上升下降子序列
待补
F. 草莓
构造题姿势水平还欠缺很多...
先考虑$n,m>1$的情况
若$n,m$中至少有一个为偶数,那么存在哈密尔顿回路;若$n,m$均为奇数,那么当$x+y$为偶数时存在哈密尔顿通路
看似跟起始位置有关,但是在第一次收集之前是可以移动一次的,于是可以保证一定能处于一条哈密尔顿通路上
然后考虑如何收集草莓
当$k<nm$时,直接走哈密顿通路即可;当$k>=nm$时,最好的情况是位置上剩余的草莓数依次为$0,1,2,...,nm-1$,而这是一定能够构造出来的:先待在原地,最后走一次哈密顿通路
当$n,m$中至少有一个为$1$时(不妨令$n=1$),考虑如何构造最优解
当$k$很大时,可以类似上面的思路,先走到一端,等到最后再走到另一端,此时各位置上剩余的草莓数依次为$0,1,2,...,m$(严格来说,范围是$k>=m+max(0,min(y-2,m-y-1))$);当$k$不足以执行上述策略时,仍然可以发现 应当将尽可能长的连续一段草莓拉满,即大体上是走向距初始位置较远的那一端,但需要先往反方向退几步

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const ll MOD=998244353,rev=499122177; ll n,m,x,y,k; int main() { int T; scanf("%d",&T); while(T--) { scanf("%lld%lld%lld%lld%lld",&n,&m,&x,&y,&k); if(n>m) swap(n,m),swap(x,y); ll ans=0; if(n==1) { if(m==1) ans=k%MOD; else { if(m+min(max(0LL,y-2),max(0LL,m-y-1))<=k) { ans=k%MOD*m%MOD; ans=ans+MOD-(m-1)*m%MOD*rev%MOD; } else { ll len=min(max(m-y+2,y+1),k); len+=(k-len)/2; ans=(k+k-len+1)*len/2; } } printf("%lld\n",ans%MOD); continue; } if(n*m<=k) { ans=(1+n*m)%MOD*n%MOD*m%MOD*rev%MOD; ans=ans+(k-n*m)%MOD*n%MOD*m%MOD; } else ans=(1+k)%MOD*(k%MOD)%MOD*rev%MOD; printf("%lld\n",ans%MOD); } return 0; }
G. 草莓2
nb队友找的结论是,对于所有$n,m$ 必存在哈密顿回路
于是当$k>=n*m$的情况,就是不停地走哈密顿回路($k>nm$时,有所有$a_i=nm$)
当$k<n*m$时,由于每一步仅会往上下左右$4$个方向走(停留在原地不最优),一共只有$4^{nm-1}$的情况,暴力枚举即可

#include <cstdio> #include <algorithm> using namespace std; typedef long long ll; const int N=10; const int dx[5]={-1,1,0,0,0},dy[5]={0,0,-1,1,0}; ll k; int n,m,sx,sy; ll a[N][N],sum; inline bool inBoard(int x,int y) { return (x>=1 && x<=n && y>=1 && y<=m); } ll ans=0,res=0; void dfs(int dep,int x,int y) { if(dep>k) { ans=max(ans,res); return; } ll save=a[x][y]; res+=save; a[x][y]=0; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) a[i][j]++; for(int i=0;i<4;i++) { int nx=x+dx[i],ny=y+dy[i]; if(inBoard(nx,ny)) dfs(dep+1,nx,ny); } for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) a[i][j]--; res-=save; a[x][y]=save; } int main() { scanf("%d%d%d%d%lld",&n,&m,&sx,&sy,&k); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%lld",&a[i][j]),sum+=a[i][j]; if(k>=n*m) { printf("%lld\n",sum+(n*m-1)*n*m/2+(k-n*m)*(n*m)); return 0; } dfs(1,sx,sy); printf("%lld\n",ans); return 0; }
H. 游戏
由于所有数对都是等价的,所以考虑某一数对出现的概率
为$\frac{C^1_{\lfloor \frac{n}{2} \rfloor}\cdot (n-2)! \cdot (\frac{1}{2})^{\lfloor \frac{n}{2}\rfloor -1}}{n!\cdot (\frac{1}{2})^{\lfloor \frac{n}{2} \rfloor}}=\frac{2\cdot \lfloor \frac{n}{2} \rfloor}{n(n-1)}$
答案就是$n^2$判断数对中互质个数再乘上这个概率;可以欧拉筛但是没必要

#include <cstdio> #include <algorithm> using namespace std; typedef long long ll; ll gcd(ll a,ll b) { if(b==0LL) return a; return gcd(b,a%b); } int n,cnt; int main() { scanf("%d",&n); if(n==1) { printf("0/1\n"); return 0; } for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) if(gcd(i,j)==1) cnt++; ll a=2LL*(n/2)*cnt,b=n*(n-1); ll tmp=gcd(a,b); printf("%lld/%lld\n",a/tmp,b/tmp); return 0; }
I. 圆
待补
J.King
待补
K. 修炼
考虑二分答案$ans$
那么第一天提升的能力值(不论是$a_1$还是$a_2$)最终会产生$ans$的贡献;第二天提升的最终会产生$ans-1$的贡献,以此类推
然后考虑如何能判定足够打boss
相当于从$1,2,...,ans-1,ans$的贡献中选出一些给$v_1$,其余的给$v_2$;由于这样的序列能构成任意数,故只要判断是否$\sum_{i=1}^{ans} i >=max(0,b_1-a_1\cdot ans)+max(0,b_2-a_2\cdot ans)$即可

#include <cmath> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; int n; ll a1,a2; int main() { scanf("%lld%lld",&a1,&a2); scanf("%d",&n); int ans=100000; for(int i=1;i<=n;i++) { ll b1,b2; scanf("%lld%lld",&b1,&b2); int l=1,r=100000,mid,res=100000; while(l<r) { mid=(l+r)>>1; ll dlt=max(0LL,b1-a1*mid)+max(0LL,b2-a2*mid); ll add=1LL*(1+mid)*mid/2; if(add>=dlt) res=min(res,mid),r=mid; else l=mid+1; } res=min(res,l); ans=min(ans,res); } printf("%d\n",ans); return 0; }
L. 图
整个图中顶点的状态最多有$2^n$种,不算很大;而且有绝大部分的状态不会出现
于是考虑bfs找出 图的状态 的循环节,然后求出余数就能得到答案了
写的时候稍微有点细节

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; struct Edge { int x,y; Edge(int a=0,int b=0) { x=a,y=b; } }; typedef long long ll; const int N=20; int n,m,q; Edge e[N*N]; int len; int ord[(1<<N)+1]; int cnt[(1<<N)+1][N],tmp[N]; int main() { scanf("%d%d%d",&n,&m,&q); int mask=0; for(int i=0;i<n;i++) { int x; scanf("%d",&x); mask|=(x<<i); } for(int i=0;i<m;i++) { scanf("%d%d",&e[i].x,&e[i].y); e[i].x--,e[i].y--; } int beg,end; memset(ord,-1,sizeof(ord)); while(1) { memset(tmp,0,sizeof(tmp)); ord[mask]=++len; for(int i=0;i<n;i++) cnt[len][i]=cnt[len-1][i]+((mask&(1<<i))>0?1:0); for(int i=0;i<m;i++) { int x=e[i].x,y=e[i].y; if(mask&(1<<x)) tmp[y]++; } int nmask=0; for(int i=0;i<n;i++) if(tmp[i]&1) nmask|=(1<<i); if(ord[nmask]>=0) { beg=ord[nmask]; end=len; len=end-beg+1; break; } mask=nmask; } while(q--) { int x; ll k; scanf("%d%lld",&x,&k); x--; if(k>cnt[end][x] && cnt[end][x]-cnt[beg-1][x]==0) { printf("-1\n"); continue; } if(k<=cnt[end][x]) { int l=1,r=end,mid,ans=end; while(l<r) { mid=(l+r)>>1; if(cnt[mid][x]>=k) r=mid,ans=min(ans,mid); else l=mid+1; } ans=min(ans,l); printf("%d\n",ans-1); continue; } ll rem=k-cnt[end][x]; ll cycle=(rem-1)/(cnt[end][x]-cnt[beg-1][x]); rem-=(cnt[end][x]-cnt[beg-1][x])*cycle; int l=beg,r=end,mid,ans=end; while(l<r) { mid=(l+r)>>1; if(cnt[mid][x]-cnt[beg-1][x]>=rem) r=mid,ans=min(ans,mid); else l=mid+1; } ans=min(ans,l); printf("%lld\n",end+1LL*cycle*len+ans-beg); } return 0; }
这次Camp还是比较锻炼的,主要是找差距和恢复状态
今年也许是最后一年了,希望能有好的结果
(待续,没补完)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号