【数学思考题】余弦定理

本来是一道相似能做的思考题，但是zyy先生讲了一种更方便的余弦定理法。故本文来记录一下余弦定理的证明。

首先，我们明确一下余弦定理的定义：余弦定理，一般是指在欧氏平面的三角形中关于三边长度和一个角度余弦值的恒等式。其形式为 $a^2 + b^2-2ab \cos \alpha=c^2 $，其中 \(\alpha\) 是a和b两边的夹角，c是第三边。余弦定理还有一个更加有对称美感的形式：\(\cos c=\dfrac{a^2+b^2-c^2}{2ab}\)。

接下来，我们讨论 \(\alpha\) 的度数，来对其进行证明。

\(\large1^{\circ}\ \alpha<90^{\circ}\)

在这里放一张图，方便理解。

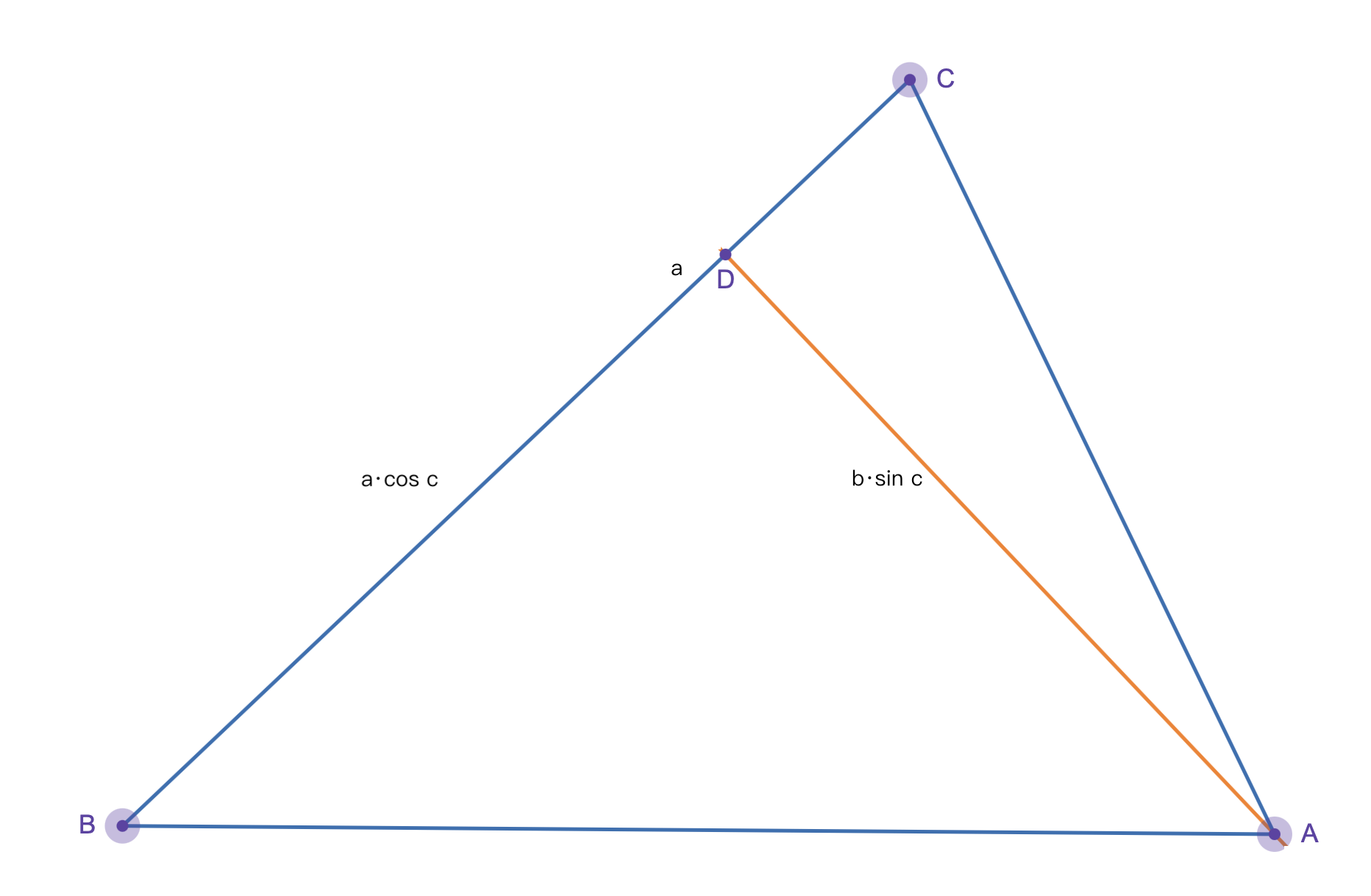
注：AD是垂直于BC的，设\(AB=c,BC=a,CA=b\)

由图，我们得到：\(c^2=(b\sin \alpha)^2+(a-b\cos \alpha)^2=b^2\sin^2\alpha+a^2+b^2\cos^2\alpha-2ab\cos\alpha\)

因为 \(sin^2\alpha+cos^2\alpha=1\)，

所以 \(a^2+b^2-2ab\cos\alpha=c^2\)，证明完毕。

\(\large2^{\circ}\ \alpha<90^{\circ}\)