【仙之人兮列如麻】函数
函数
本文的全部部分将重写。
0x00 坐标系
在开始讨论函数前,我们必须明确一个概念——坐标系。这对后面学习函数有着很大的重要性。
当然坐标系分为很多种,例如极坐标系、空间坐标系、平面直角坐标系等等。当然我们讨论的是平面直角坐标系。
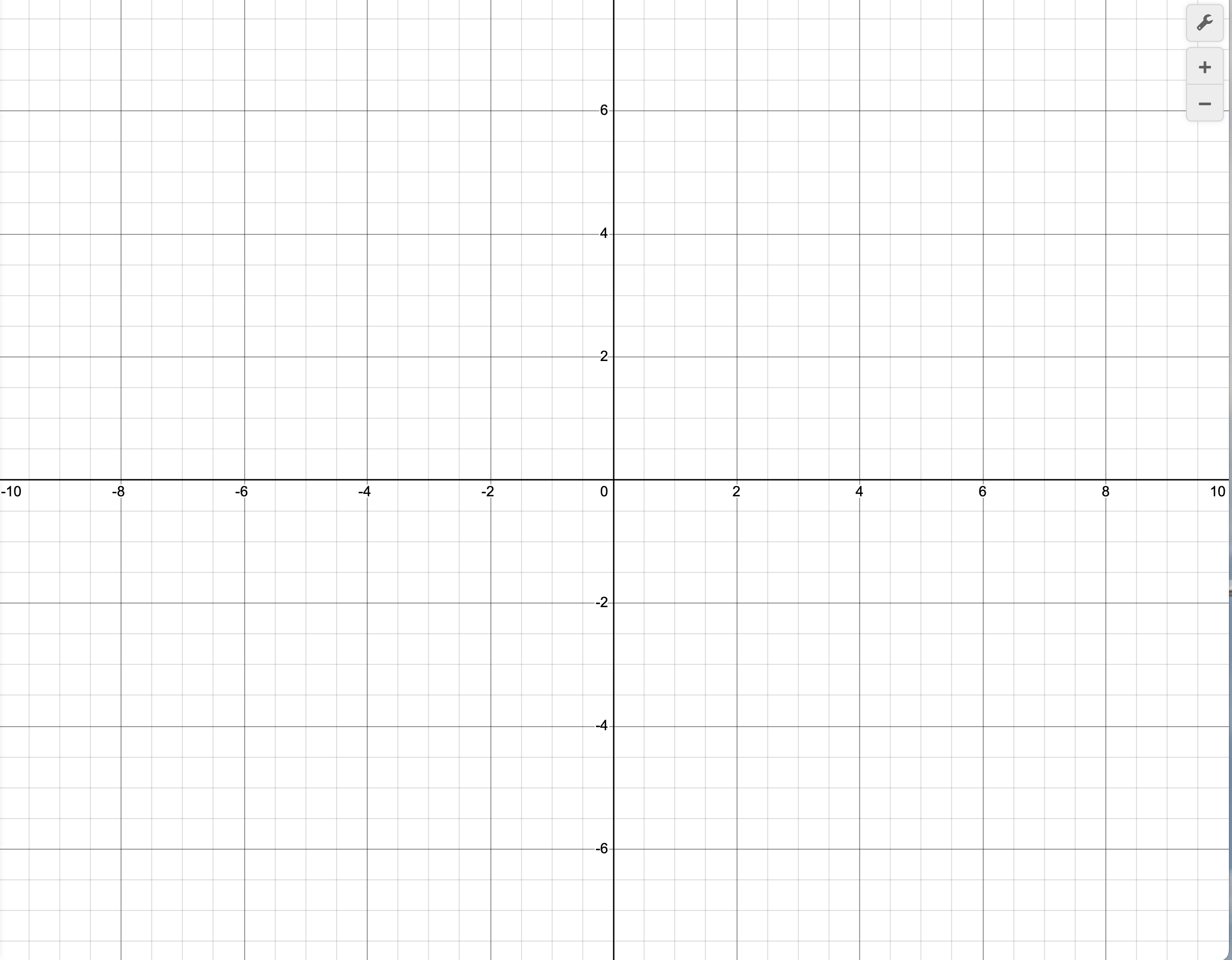
我们可以看到在坐标系上有两条轴。这就是横轴与纵轴。用字母 \(x\) 和 \(y\) 表示。每条轴上都用相等的距离来划定单位。平面上的每个点都可以用一个单独的坐标来表示。如点 \((3,5)\)或者点 \((-\dfrac{114514}{1919810},1)\) 都是可以表示出来的。
随后我们来看一个概念,那就是变量。来看一个表达式:
这就是一次函数的一般形式。期中 \(y\) 和 \(x\) 称作变量,前者受后者的值的控制,因此称为“因变量”;后者因为控制其他变量的值,自身值不变,因此称为“自变量”。这就是变量的概念。
接下来看如何画出函数的图象。还是那刚才那个东西来举例。我们设一次函数 \(y=x+1\),随后我们按照三步走:列表、标点、连线。我们可以给 \(x\) 赋不同的值,让函数获得不同的结果,随后在对应的位置(点 \((当前的x,函数值y)\))标上一个点。一般不需要标多,两个点足以确定一条直线,因此标两个分别和纵轴和横轴重合的点即可。接下来用函数工具给大家展示一下刚才那个一次函数的图像:
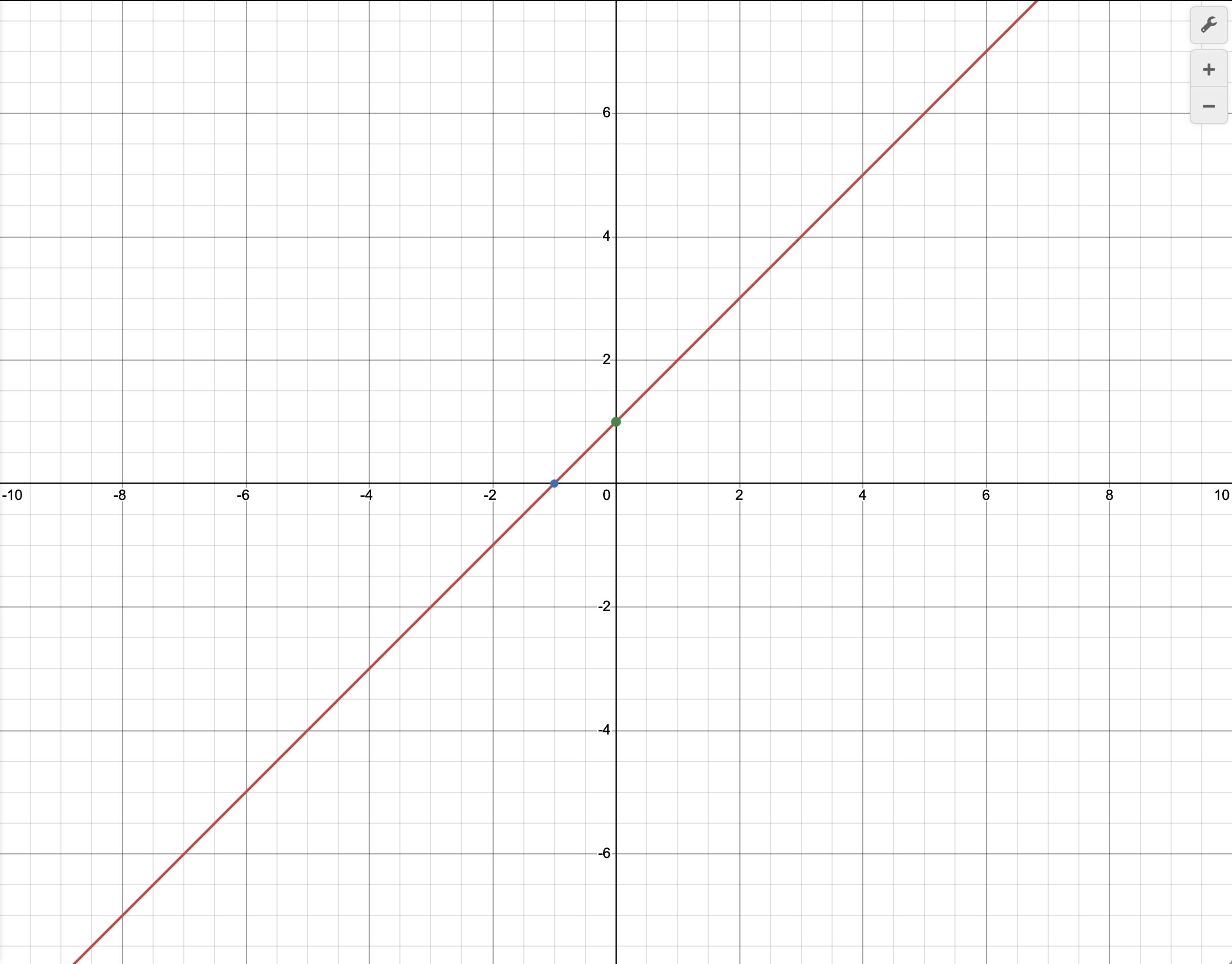
其中两个点便是上文提到的与横轴、纵轴重合的点。红色的直线是函数图象。
更重要的一点是关于“象限”的定义。整个平面被两条轴分成了四个部分,右上角的是第一象限,随后以逆时针编号为2、3、4象限。
0x01 正比例函数与一次函数
正比例函数的图像是一条直线,并且关于原点中心对称。其一般形式为 \(y=kx(k\neq 0)\)。函数图象经过原点。
函数定义域为 \((-\infty,+\infty)\)。
对于正比例函数的图像,恒过原点,其陡峭程度是根据 \(k\) 的大小来决定的。
一次函数的图像是过 \((0,b)\) 和 \((-\dfrac{b}{k},0)\) 的一条直线。其一般形式为 \(y=kx+b(k\neq 0)\)。当 \(b=0\) 时称作上面的正比例函数。
函数定义域为 \((-\infty,+\infty)\)。
将一次函数解析式中的 \(y\) 移项就能得到一个二元一次方程。此刻适合一次函数的一组变量 \(x、y\) 就是这个二元一次方程的一组解。
来看一下有关于平移图像的题目。
\(\Large\mathbf{P}\)\(\mathbf{ROBLEM}\) \(1\)
将正比例函数 \(y=2x\) 的图象向右平移三个单位,求平移后的函数解析式。
\(\Large\mathbf{sol}\)
因为正比例函数的图像恒过原点,所以平移后一定过点 \((3,0)\)。令我们所求的函数解析式为 \(y=2x+b\)。再用到一个规律,就是“左加右减,上加下减”。我们是向右平移三个单位,因此解析式要变成 \(y=2(x-3)\)。因此我们得出 \(b=-6\)。综上,平移后的解析式为 \(y=2x-6\)。
随后来看一道关于焦点的题目。
\(\Large\mathbf{P}\)\(\mathbf{ROBLEM}\) \(2\)
已知关于 \(x\) 的方程 \(kx+3=|x+1|-2|x-1|+|x+2|\) 有三个解,求 \(k\) 的取值范围。
\(\Large\mathbf{sol}\)
刚开始看这道题,我们可能没有很多头绪。但是稍微转变一下,方程左边是一次方程的一般形式,右边是一个分段函数,那我们就可以转换成两个函数有三个交点。这就很好做了,画出图像即可。
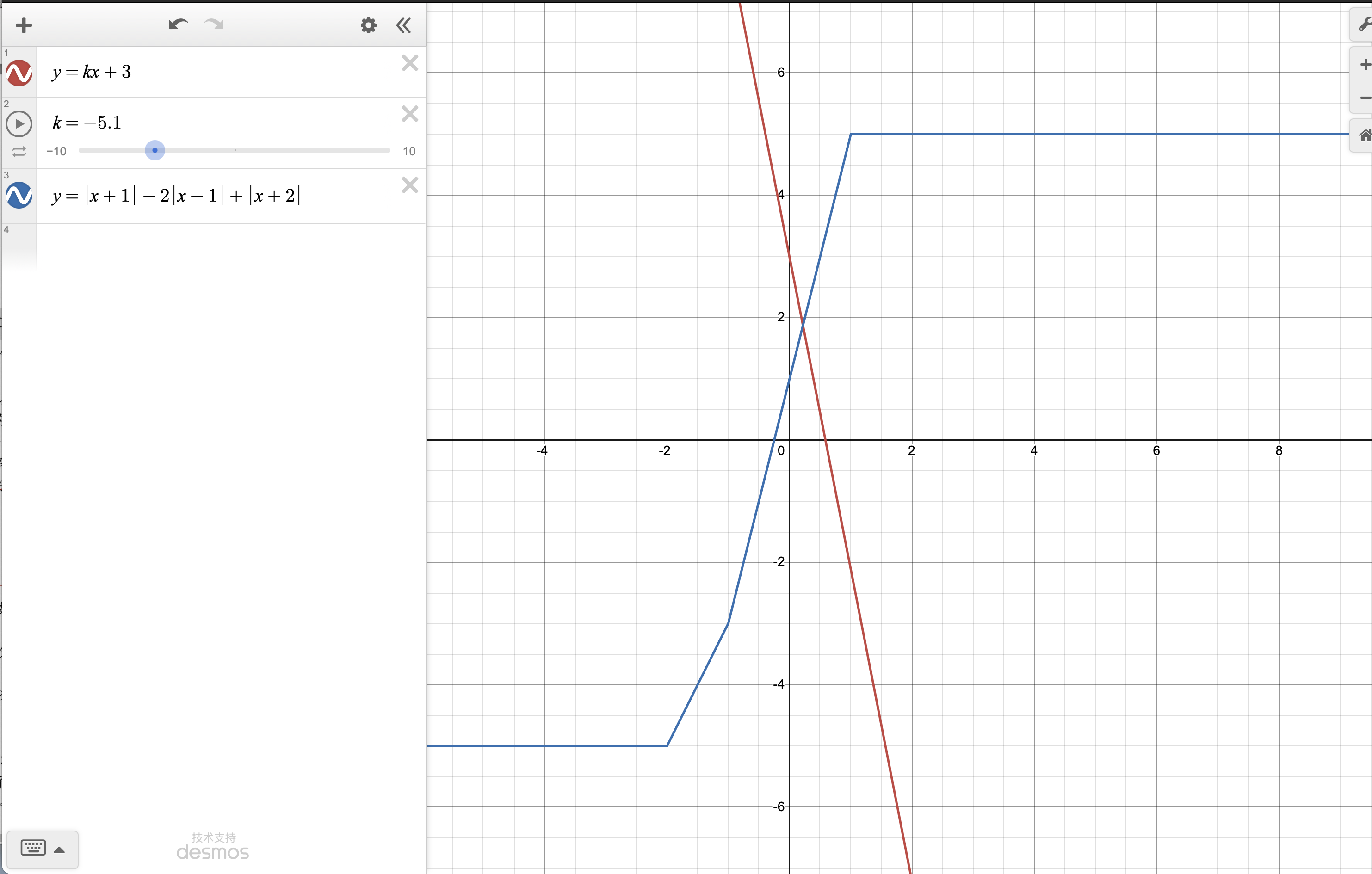
图中红色线是一次函数,蓝色线就是那个带绝对值的分段函数,运用分段函数还可以求绝对值得最小值。
网址放在这了,大家可以进去拖动一下 k 的值,自行尝试一下:https://www.desmos.com/calculator/n4itxrqmw8?lang=zh-CN
拖动后我们发现,在 \(0<k<2\) 时两个函数有三个交点。尽管有时看不出来,但是他们在无限远的地方仍然有一个交点。缩小就能看到了。
那么这道题就接完了。
\(\Large\mathbf{P}\)\(\mathbf{ROBLEM}\) \(3\)
求 \(|x+1|+|x+2|+|x+3|+|x+4|+|x+5|\) 的最小值。
\(\Large\mathbf{sol}\)
这道题有一个老师教我的方法,那就是首尾相接。
不知道怎么描述所以我就放图片了。
当然我们也能用分段函数来求。
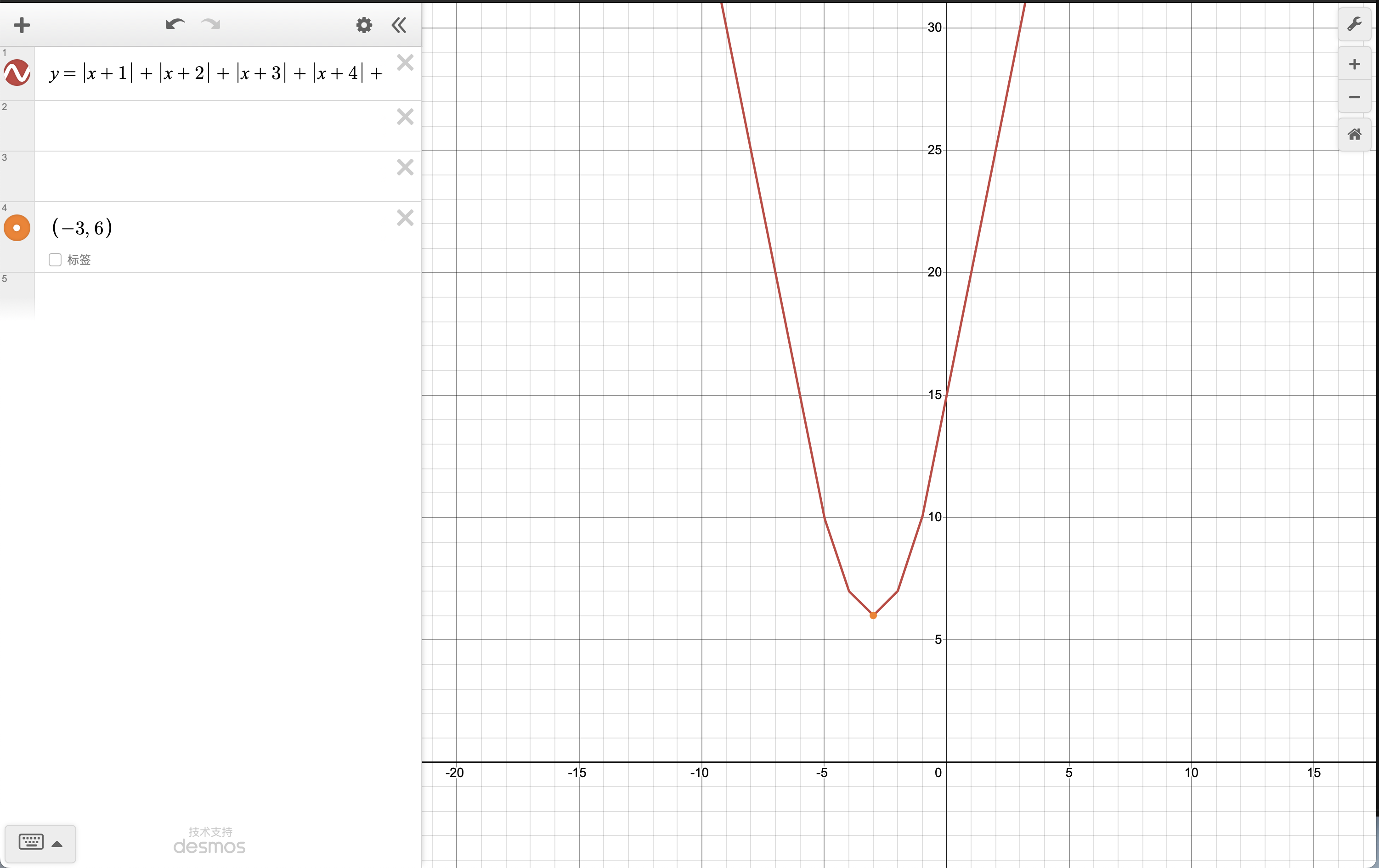
可以看到,这个函数是没有最大值的。它向着无穷大一跑去。可以看到函数图象的最低点是6,因此原式的最小值是6。
如果你在考场上遇到这个题,那么我建议用绝对值得几何意义来做。因为花分段函数实在是太麻烦了,如果你有大时间可以尝试锻炼一下自己的作图功力。(手动划去)
\(\Large\mathbf{P}\)\(\mathbf{ROBLEM}\) \(4\)
如果一次函数的图像经过点 \((2,2)\),它与两坐标轴的面积为1,求该一次函数的解析式。
\(\Large\mathbf{sol}\)
设一次函数为 \(y=kx+b\)。因为其经过点 \((2,2)\),因此我们可以将其带入得到 \(2k+b=2\)。又因为我们知道一次函数交坐标轴于点 \((-\dfrac{b}{k},0)\) 和 \((0,b)\),因此根据三角形面积公式,我们可以得到:
化简可得 \(b^2=2\left|\ k\ \right|\)。
根据上面的函数解析式,我们能得到一个方程组:
解方程组,可以得到两组解,因为b是二次项。
综上,函数的解析式是
\(\Large\mathbf{P}\)\(\mathbf{ROBLEM}\) \(5\)
设 \(a\) 是整数,且关于 \(x\) 的方程 \(||x-1|-2|\) 有且仅有三个不同的整数解,求 \(a\)。
\(\Large\mathbf{sol}\)
本题是一道很好的分段函数题。两种思路,第一种化简绝对值,根据得到的三个结果来看a可能的取值,或者就是画分段函数的图像,看有没有三个整点在同一条直线上。
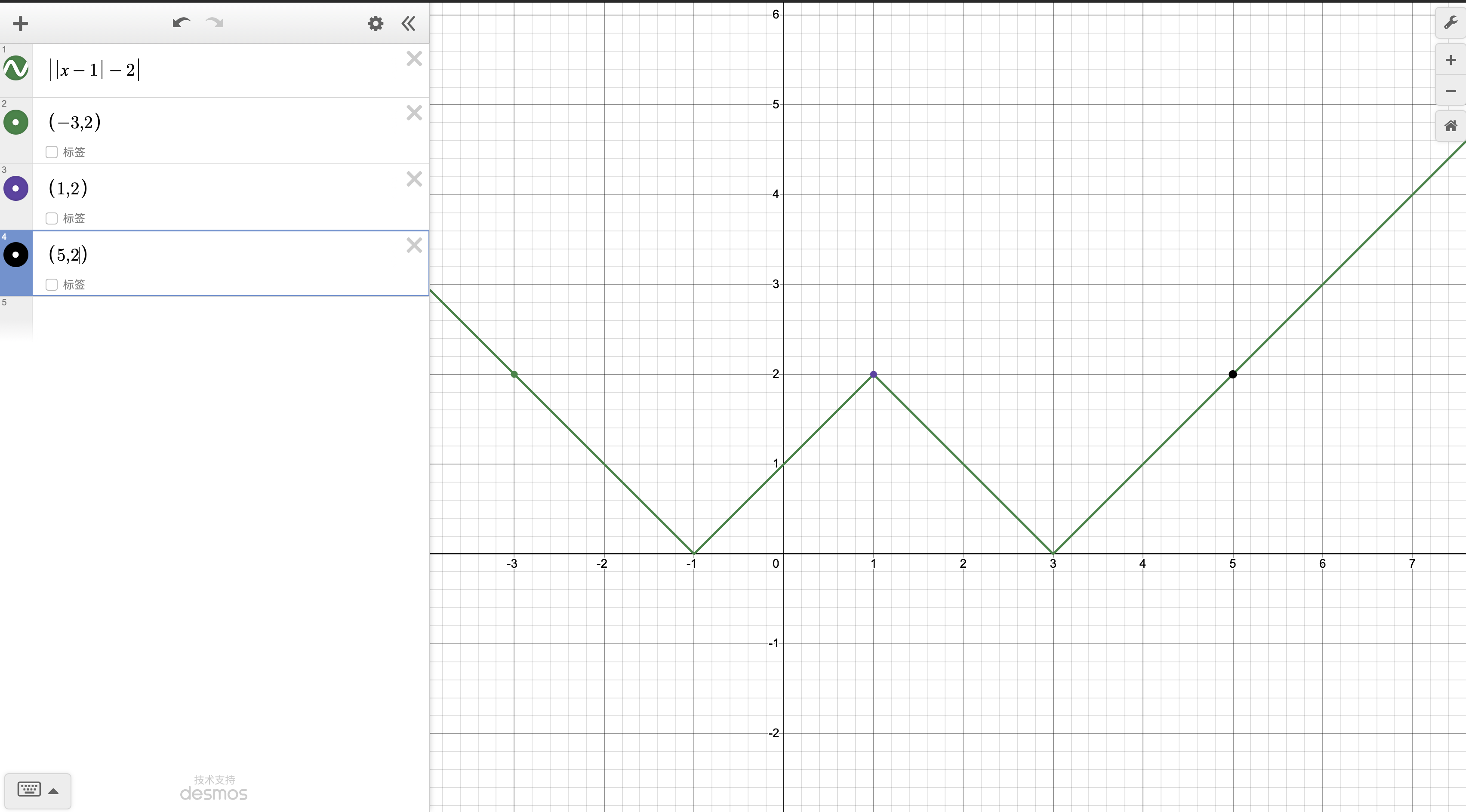
可以看到的确有三个点符合要求,于是我们得出,当且仅当 \(a=2\) 时,符合题意。因为往下走,只有两个点;往上走也是只有两个点。
\(\Large\mathbf{P}\)\(\mathbf{ROBLEM}\) \(6\)
已知曲线由方程 \(|x-1|+|y-1|=1\) 确定,求曲线所围成图形的形状及面积。
\(\Large\mathbf{sol}\)
先化简绝对值然后画图像即可。我们理论上可以得到四条一次函数:
- \(y=-x+3\);
- \(y=x-1\);
- \(y=x+1\);
- \(y=-x+1\).
然后根据这四个函数画图像即可。
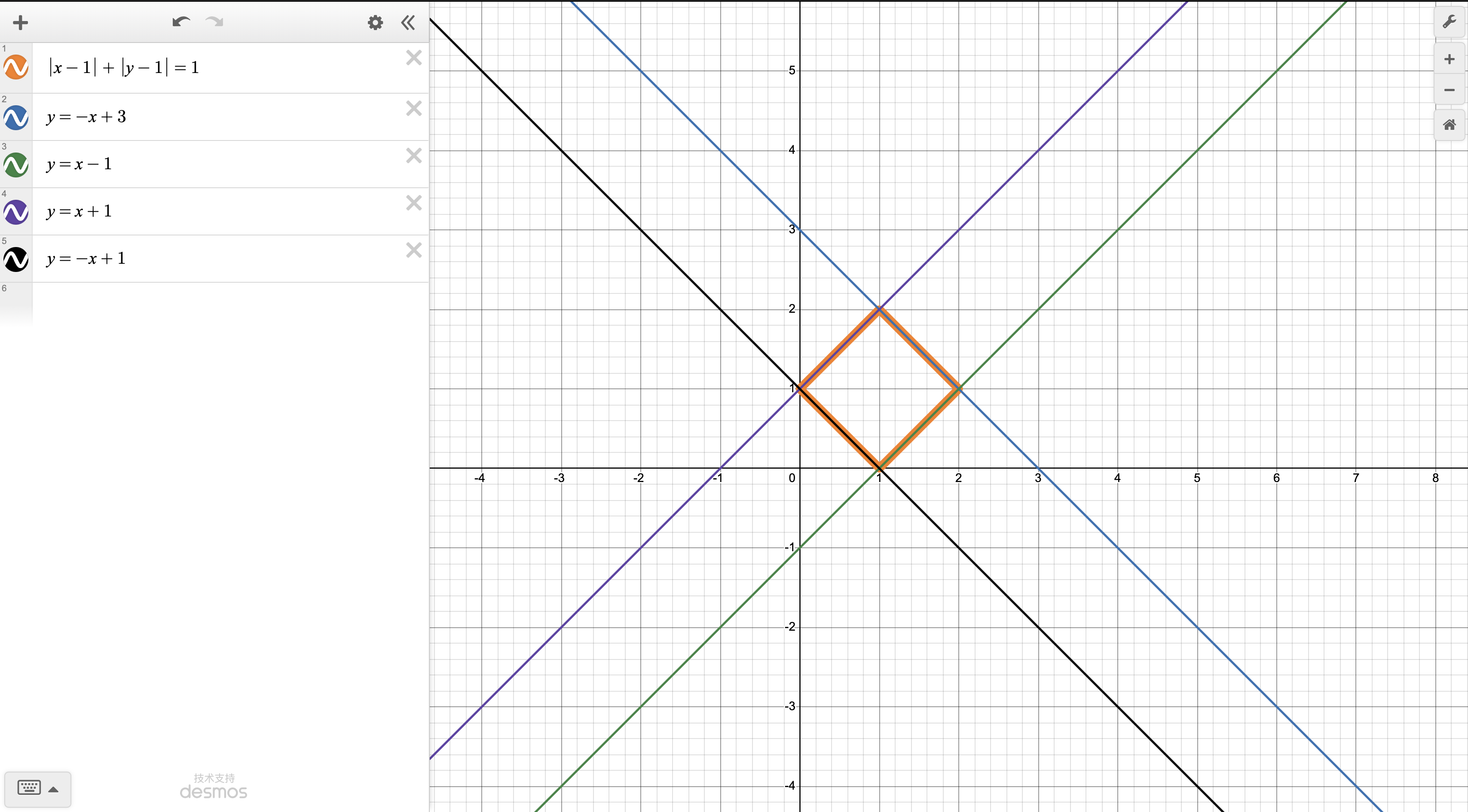
可以看到四条函数聚合成了一个正方形,并且和直接输入原题表达式所构成的图形一致。(仅考虑重合部分)
正方形确定完毕,我们来求面积。这个简单,对角线乘积,\(2\times2\times\dfrac{1}{2}=2\) 或者用勾股定理 \(a^2+b^2=c^2\),在左下角那个小的三角形中可以求出 \(c=\sqrt2\),也就是正方形的边长。用 \(S=a^2\) 计算也可以。
0x02 反比例函数与二次函数
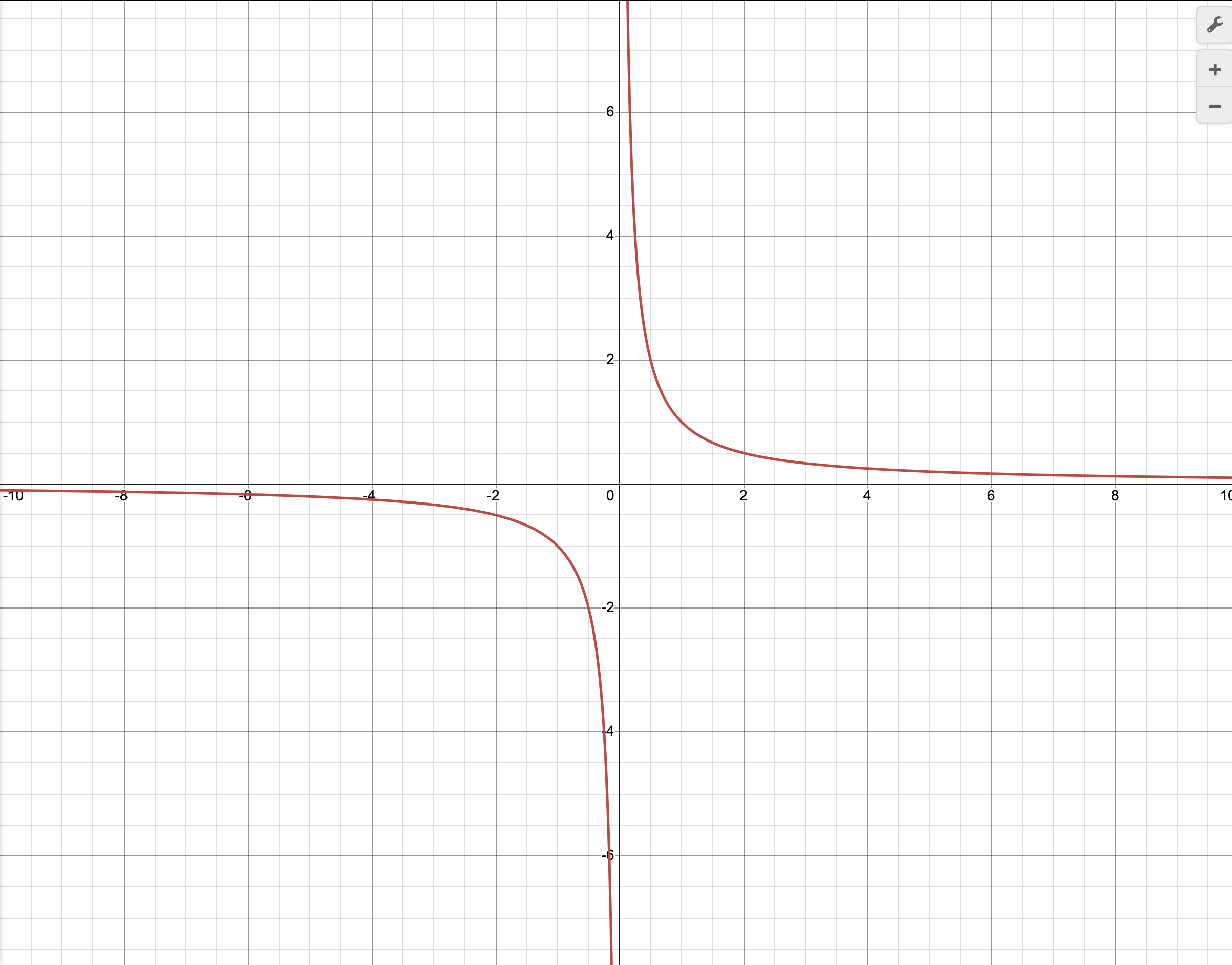
先来看反比例函数。其形如 \(y=\dfrac{k}{x}\)。图像是非常魔幻的双曲线。对于图像,当k大于0时图像在1、3象限内,小于则在2、4象限里。
接下来就是整个初中里面的重头戏了——二次函数。这个东西有很多繁杂的概念和知识点,就是我们学校这一精简教材也用了近300页的篇幅去写。
首先是一般形式:
其中有三个参数。这三个参数的作用也各不相同:\(a\) 控制着图像(抛物线)的开口大小,\(b\) 控制着抛物线对阵轴的位置,\(c\) 则控制图像和 \(y\) 轴的交点位置。如果a=0了那么二次函数就退化成为一条直线,不是二次函数了。
这是一般形式,当然还有一种东西叫做顶点式。形如
\(y=f(x)=a(x-h)^2+k\)
其中 \(h、k\) 满足 \(h=-\dfrac{b}{2a}\),\(k=\dfrac{4ac-b^2}{4a}\)。或许你会发现一些和一元二次方程求根公式很像的东西,确实是这样的。
当然还有一种比较小众的解析式名为“交点式”。其一般形式为:
\(y=f(x)=a(x-x_1)(x-x_2)\)
其中两个带下角标的参数分别代表这个二次函数的零点(即这个二次函数转换成一元二次方程后的解)。当然这种式子是有限制的,那就是原一元二次方程必须有实数解,不然连解都求不出来那就没办法写出这个式子了。因此这个式子比较小众。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号