AC 自动机学习笔记
NLC AK IOI
前置芝士:KMP 模式匹配
强烈推荐 N 总写的博客!!!!
KMP 算法,又称模式匹配算法,能够在线性时间内判定字符串 \(A[1]\)~\(A[N]\) 是否为字符串 \(B[1]\)~\(B[M]\) 的字串,并求出字符串 \(A\) 在字符串 \(B\) 中各次出现的位置。
首先考虑朴素的 \(O(NM)\) 做法。尝试枚举字符串 \(B\) 中的各个位置 \(i\) ,把字符串 \(A\) 与字符串 \(B\) 的后缀 \(B[i]\)~\(B[M]\) 对齐,向后逐一扫描比较是否相等。这种比较过程被称为 \(A\) 与 \(B\) 尝试进行“匹配”。代码如下:
char a[N],b[M];
for(int i=1;i<=m;i++)
{
bool ok=true;
for(int j=1;j<=n;j++)
if(a[j]!=b[i+j-1])
{
ok=false;
break;
}
}
可以发现,对于朴素的做法,时间复杂度的瓶颈主要在于每次匹配失败后就再从第 \(1\) 位开始匹配。如下图所示:
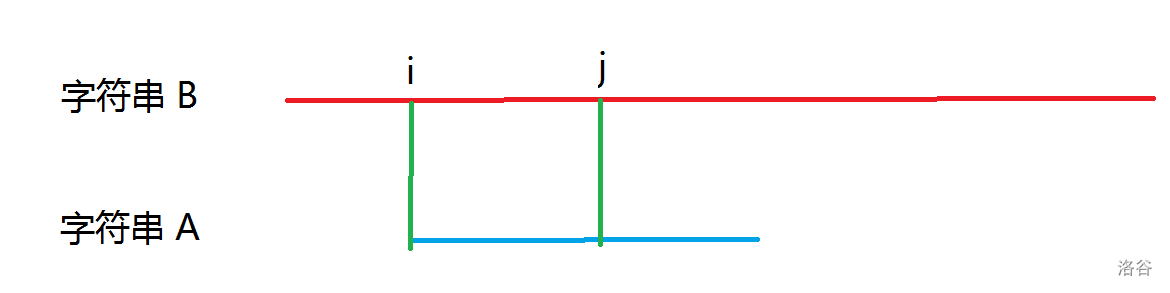
字符串 A 和 字符串 B 在 第 \(i\) 位到第 \(j\) 位完全一样,但是在第 \(j+1\) 位就不一样了。此时对于朴素的做法,就会从第 \(i+1\) 位开始重新匹配。但是显然这样是没必要的。
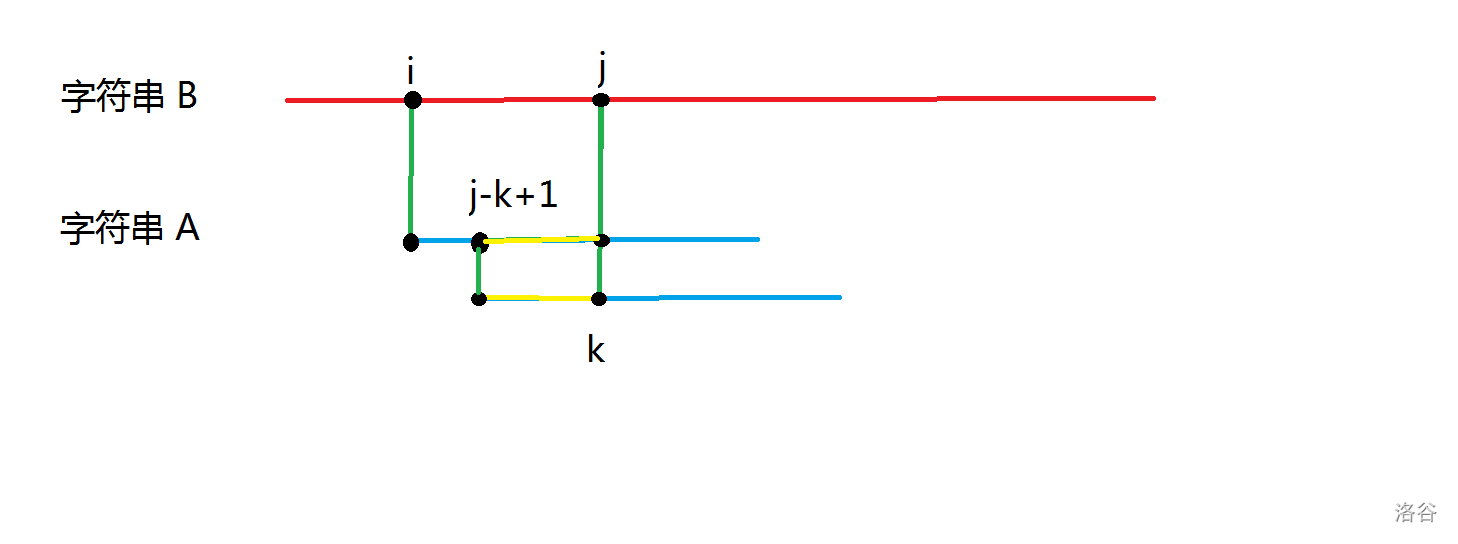
如图所示,如果字符串 \(A\) 的第 \(j-k+1\) 位到 第 \(j\) 位和第 \(1\) 位到第 \(k\) 位是匹配的,那么自然字符串 \(A\) 的第 \(1\) 位到第 \(k\) 位和字符串 \(B\) 的第 \(j-k+1\) 位到第 \(j\) 位也是匹配的,那么就省去了重头开始匹配的时间。
定义 \(next[j]\) 表示字符串 \(A[j]\) 的前缀和以 \(i\) 结尾的非前缀字串匹配的最大长度。如下图所示:
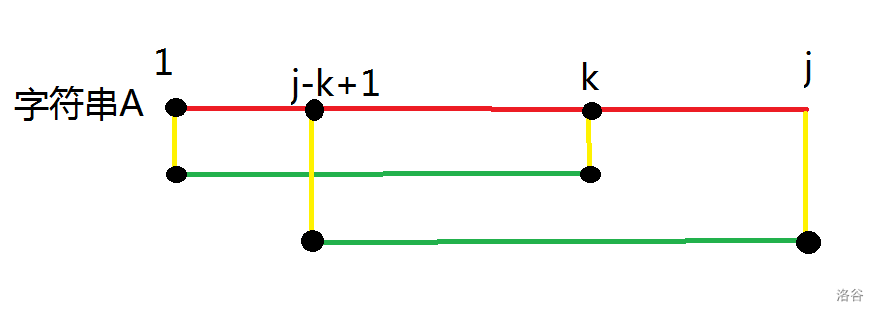
令 \(k=next[j]\),那么字符串 \(A\) 的第 \(1\) 位到第 \(k\) 位就和第 \(j-k+1\) 到第 \(j\) 位就是匹配的。
下面讨论 \(next\) 数组的计算方式。根据定义,这里的后缀不能是整个字符串,所以 \(next[1]=0\)。
可以发现,求 \(next\) 数组的朴素做法和上面的朴素匹配算法类似。考虑对匹配失败时的操作进行优化,如下图所示:
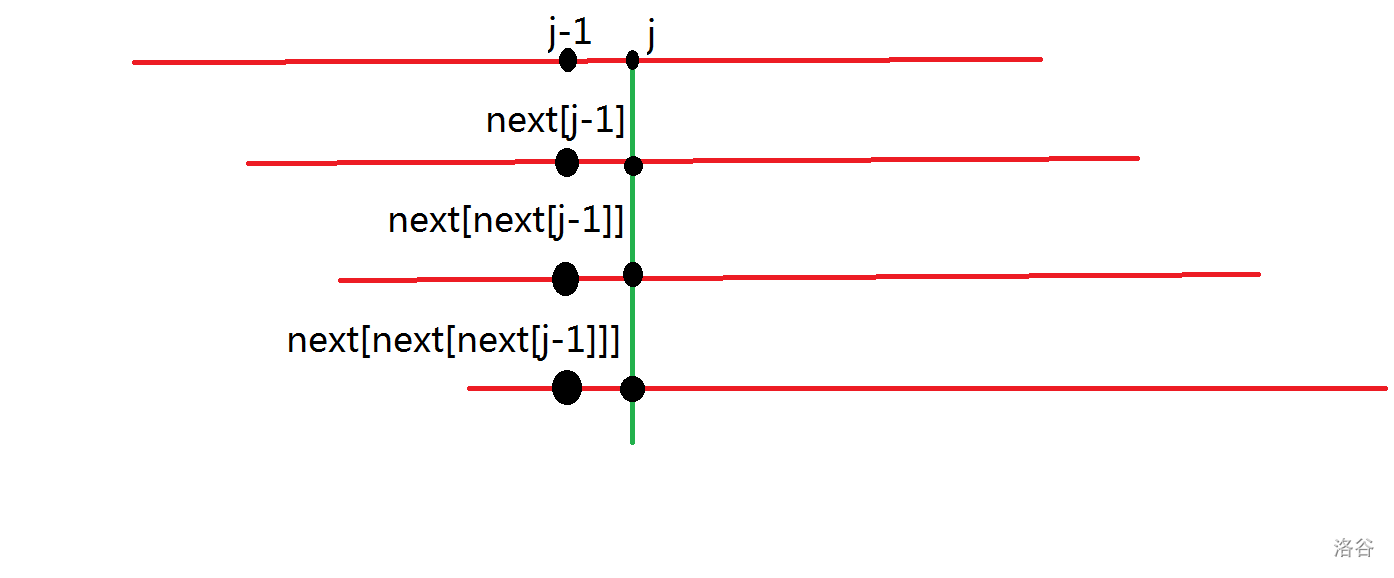
假设现在已经求出了 \(next[j-1]\)。为了方便表示,令 \(k_0=next[j-1]\),那么第 \(1\) 位到第 \(k_0\) 位就和第 \(j-k_0\) 位到第 \(j-1\) 位匹配。
如果现在 \(s[j]=s[k_0+1]\),那么就可以得到 \(next[j]=next[j-1]+1\)。
而当 \(s[j] \ne s[k_0+1]\)时,那么就只能退而求其次。在上图中绿线左侧部分,竖着一列对下来的字符都相同。于是就可以令 \(k_1=next[k_0]\),自然第 \(1\) 位到第 \(k_1\) 位和第 \(k_0-k_1+1\) 位到第 \(k_0\) 位是匹配的。那么现在只需判断 \(s[j]\) 是否和 \(s[k_1+1]\) 相等,如果不相等,直接继续令 \(k_2=next[k_1]\),继续判断即可。
接下来就可以得到 KMP 算法的完整代码了:
#include<bits/stdc++.h>
using namespace std;
const int M=1001000;
char a[M],b[M];
int ma,mb,kmp[M],k;
int main()
{
cin>>a+1>>b+1;//这里的字符串a和字符串b与上面的含义是相反的
ma=strlen(a+1);
mb=strlen(b+1);
for(int i=2;i<=mb;i++)//求next数组 next[1]=0
{
while(k&&b[i]!=b[k+1]) k=kmp[k];//如果到k=0时还是无法匹配,直接退出即可
if(b[k+1]==b[i]) k++;//因为还可能存在一个字符串都匹配不了的情况
kmp[i]=k;
}
k=0;
for(int i=1;i<=ma;i++)
{
while(k>0&&b[k+1]!=a[i]) k=kmp[k];//这里的i其实就是最上面的例子里的i+1
if(b[k+1]==a[i]) k++;
if(k==mb)
{
cout<<i-mb+1<<endl;
k=kmp[k];
}
}
for(int i=1;i<=mb;i++) cout<<kmp[i]<<" ";
cout<<endl;
return 0;
}
AC 自动机=Trie+KMP
AC 自动机能解决什么问题?
以【模板】AC 自动机为例。AC 自动机可以求出求有多少个不同的模式串在文本串里出现过。通俗地讲,就是给出一篇文章和多个单词,求有多少个单词在文章中出现过。
以单词she,he,say,shr,her和文章yasherhs为例。先对单词构造一棵 Trie,如下图所示。
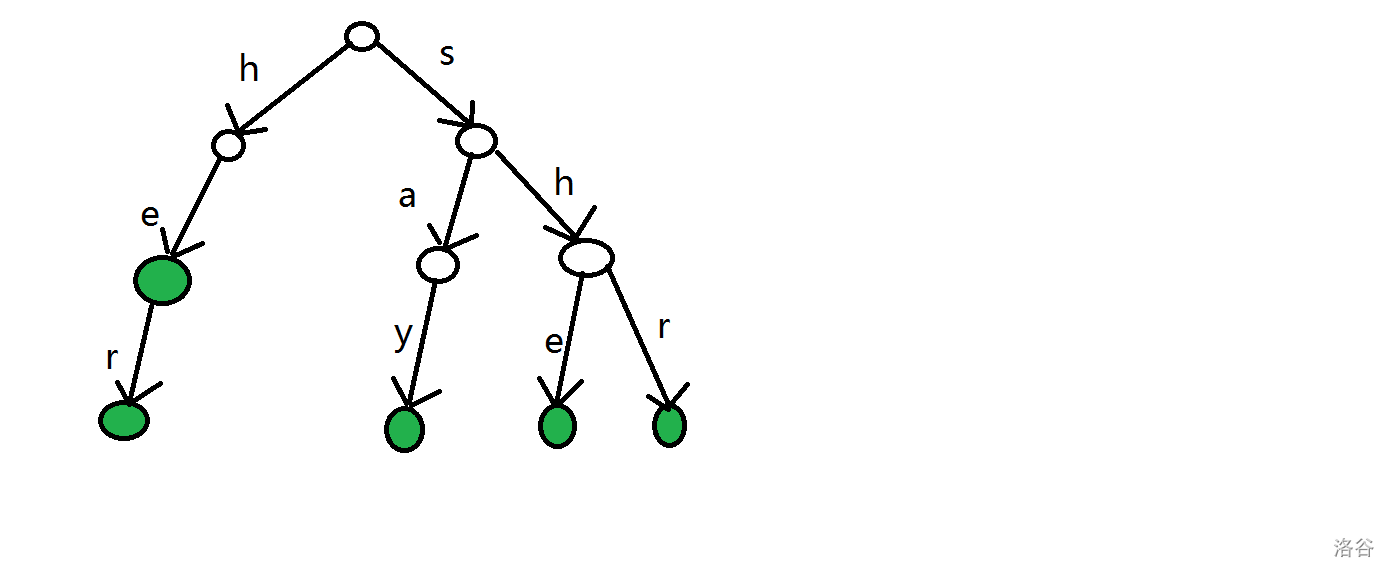
再对这些字符串求一个 \(next\) 数组,但是不同于普通的 KMP 算法(可以将 KMP 算法的字符串看成是在 Trie 上的一条链),这里的 \(next\) 数组存的是一个节点编号,也就是当前字符串匹配的最长前缀字串的最后一个字符的编号,同时这个前缀不要求和字符串在同一条链上。这样说有点难以理解,下图以 she 为例:
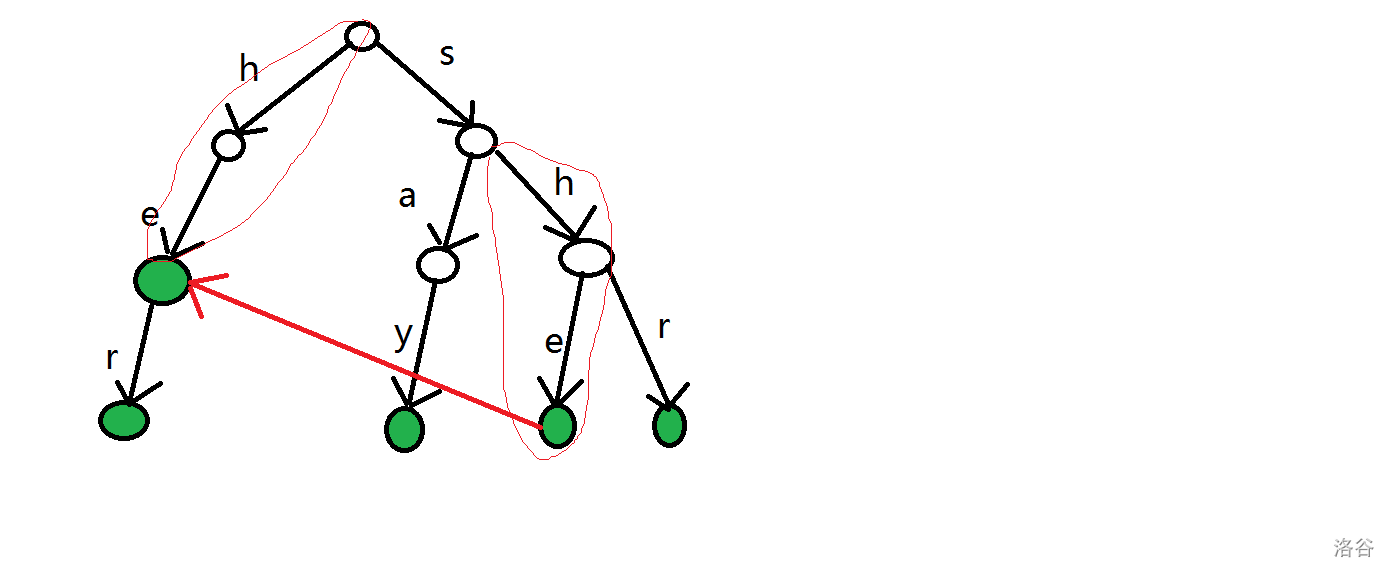
可以看到第四层的 \(e\) 指向的是 第三层的 \(e\),同时这两个 \(e\) 并不在一条链上(也就是不在同一个字符串内)。
下面来讨论一下此时的 \(next\) 数组的存法。
类比一下普通 KMP 算法中的 \(next\) 数组的求法,是从前往后一个一个枚举的,同时每次枚举开始的是 \(next[i-1]\),也就是由 \(next[i-1]\) 的信息来推出 \(next[j]\)。于是在 Trie 中也是一层一层从上往下求解,也就是用第 \(i-1\) 层的信息来推出第 \(i\) 层的信息。也就是将普通的 KMP 算法中的 for 循环扩展成 BFS。再将其他步骤类比过来,就可以得到 AC 自动机中求 \(next\) 数组的做法:
//把普通KMP算法也贴上来,便于类比理解
{
for(int i=2,j=0;i<=m;i++)
{
// j=ne[i-1]; 这一可以省略,因为在上一次循环中的next[i]就是j
while(j&&p[i]!=p[j+1]) j=ne[j];
if(p[i]==p[j+1]) j++;
ne[i]=j;
}
}
//AC 自动机中求next数组
{
for(int i=0;i<26;i++)
if(tr[0][i]) q.push(tr[0][i]);
while(q.size())//BFS的基本格式
{
int t=q.front();//t 为上面的 i-1
q.pop();
for(int i=0;i<26;i++) //i 为上面的p[i]
{
int c=tr[t][i]; //c 为上面的i
if(!c) continue; //因为这里枚举的是每一个子节点,如果是空直接返回即可
int j=ne[t];// 为上面的 j=ne[i-1]
while(j&&!tr[j][i]) j=ne[j];//!tr[j][i]就是p[i]!=p[j+1],上面的不等于在此处就是不存在
if(tr[j][i]) j=tr[j][i];//如果匹配成功了,就把j变成匹配成功的前缀字符串的最后一个字符的编号
ne[c]=j; //ne[i]=j
q.push(c);//求下一层的时候会用到,这里是不同于普通KMP算法的地方
}
}
}
//这一部分比较绕,需要多理解几遍,也可以画图理解,最好是先完全理解KMP算法的思想,这样就比较好懂了
结合图理解一下:
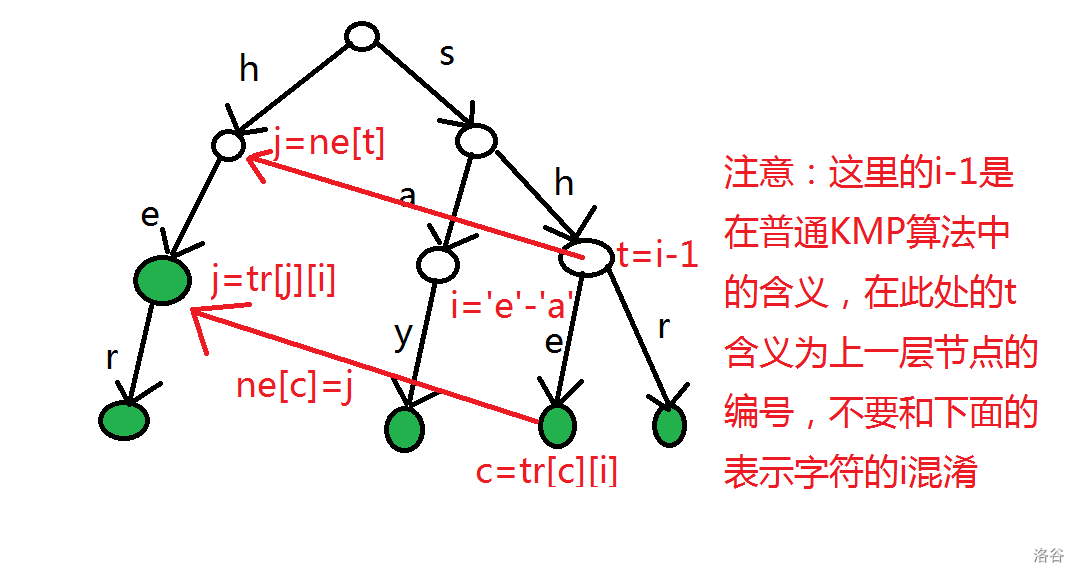
接着是类比普通 KMP 算法中匹配的部分。
//可以理解为单词在文章中进行匹配
{
int res=0;//res为出现的单词的种类的个数
for(int i=0,j=0;i<strlen(s);i++)//字符串s就是文章,从Trie的根节点开始匹配
{
int t=s[i]-'a';//当前文章最后一个字符
while(j&&!tr[j][t]) j=ne[j];//对于当前的文章求在Trie中的匹配
if(tr[j][t]) j=tr[j][t];//此时的j就是当前文章在Trie中匹配的前缀字串深度最大的节点的编号
//下面是AC自动机特有的步骤,可以借助图理解一下
int p=j;//既然当前的文章能匹配到以j结尾的字符串,那么这个字符串的前缀字串显然也可以匹配到
while(p)
{
res+=cnt[p];
cnt[p]=0;//统计的是出现的单词的种类的个数,而不是单词出现的次数
p=ne[p];
}
}
}
同样借助图理解一下:
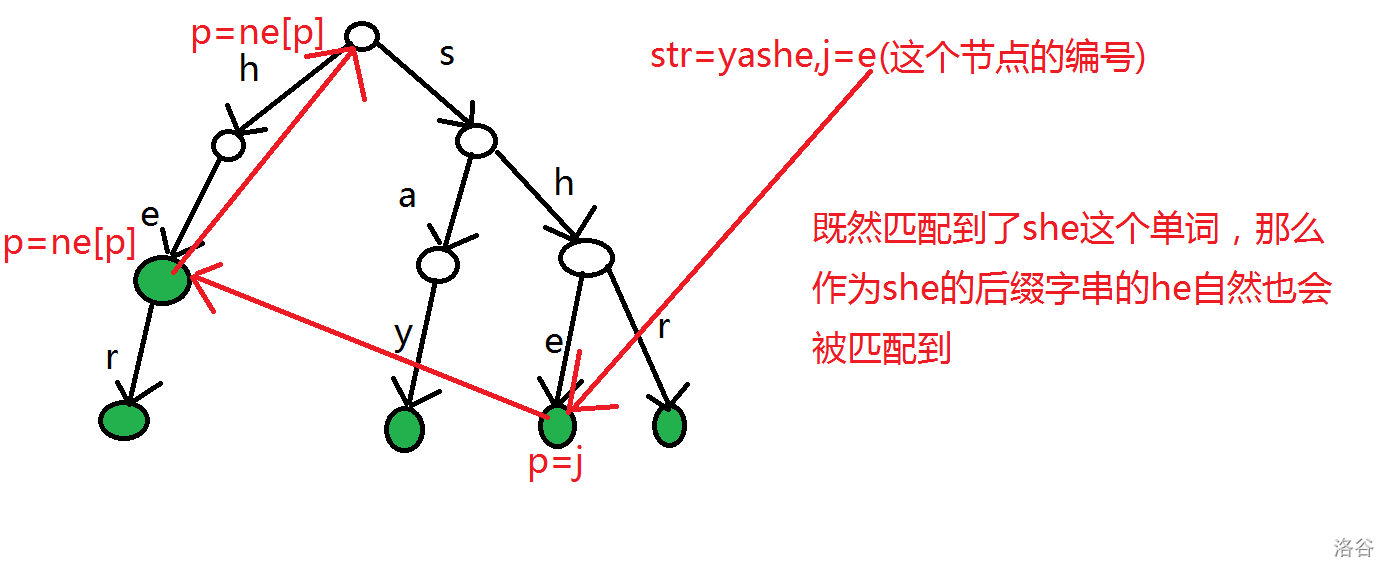
完整code:
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
const int N=1e4+10;
const int S=55;
const int M=1e6+10;
char s[M];
int num,n,tr[N*S][26],cnt[N*S],ne[N*S];
void init()
{
memset(tr,0,sizeof(tr));
memset(cnt,0,sizeof(cnt));
memset(ne,0,sizeof(ne));
num=0;
}
void insert()
{
int p=0;
for(int i=0;i<strlen(s);i++)
{
int v=s[i]-'a';
if(!tr[p][v]) tr[p][v]=++num;
p=tr[p][v];
}
cnt[p]++;
}
void build()
{
queue<int> q;
for(int i=0;i<26;i++)
if(tr[0][i]) q.push(tr[0][i]);
while(q.size())
{
int t=q.front();
q.pop();
for(int i=0;i<26;i++)
{
int c=tr[t][i];
if(!c) continue;
int j=ne[t];
while(j&&!tr[j][i]) j=ne[j];
if(tr[j][i]) j=tr[j][i];
ne[c]=j;
q.push(c);
}
}
}
int main()
{
init();
scanf("%d",&n);
while(n--)
{
scanf("%s",s);
insert();
}
build();
scanf("%s",s);
int res=0;
for(int i=0,j=0;i<strlen(s);i++)
{
int t=s[i]-'a';
while(j&&!tr[j][t]) j=ne[j];
if(tr[j][t]) j=tr[j][t];
int p=j;
while(p)
{
res+=cnt[p];
cnt[p]=0;
p=ne[p];
}
}
printf("%d\n",res);
return 0;
}
但是此代码并不能通过简单版的数据。。。于是还需要考虑优化。
Trie 图
将 AC 自动机优化成 Trie 图。主要在于对求 \(next\) 数组时的优化。
这是原来的代码:
for(int i=0;i<26;i++)
{
int c=tr[t][i];
if(!c) continue;
int j=ne[t];
while(j&&!tr[j][i]) j=ne[j];
if(tr[j][i]) j=tr[j][i];
ne[c]=j;
q.push(c);
}
这是优化后的代码:
for(int i=0;i<26;i++)
{
int c=tr[t][i];
if(!c) tr[t][i]=tr[ne[t]][i];
else
{
ne[c]=tr[ne[t]][i];
q[++tt]=c;
}
}
具体优化了什么呢,对于下面的图:
上面的优化的一部分就是对于 \(j=ne[j]\) 这一步的优化,也就是省去了 \(j\) 一步一步往上跳的步骤,有点类似于并查集的路径压缩优化。而对于该节点为空的情况,直接把这个点赋值为父节点的 \(next\) 对应的点上。这样就可以省去很多时间。
同样的,对于查找匹配前缀字串:
while(j&&!tr[j][t]) j=ne[j];
if(tr[j][t]) j=tr[j][t];
也可以直接优化为:
j=tr[j][t];
优化后的完整 code:
#include<cstdio>
#include<cstring>
using namespace std;
const int N=1e4+10;
const int S=55;
const int M=1e6+10;
char s[M];
int num,n,tr[N*S][26],cnt[N*S],ne[N*S],q[N*S];
void insert()
{
int p=0;
for(int i=0;s[i];i++)
{
int v=s[i]-'a';
if(!tr[p][v]) tr[p][v]=++num;
p=tr[p][v];
}
cnt[p]++;
}
void build()
{
int hh=0,tt=-1;
for(int i=0;i<26;i++)
if(tr[0][i]) q[++tt]=tr[0][i];
while(hh<=tt)
{
int t=q[hh++];
for(int i=0;i<26;i++)
{
int c=tr[t][i];
if(!c) tr[t][i]=tr[ne[t]][i];
else
{
ne[c]=tr[ne[t]][i];
q[++tt]=c;
}
}
}
}
int main()
{
scanf("%d",&n);
while(n--)
{
scanf("%s",s);
insert();
}
build();
scanf("%s",s);
int res=0;
for(int i=0,j=0;s[i];i++)
{
int t=s[i]-'a';
j=tr[j][t];
int p=j;
while(p&&cnt[p]>-1)//其实就是不走重复点
{
res+=cnt[p];
cnt[p]=-1;
p=ne[p];
}
}
printf("%d\n",res);
return 0;
}
应用 修复DNA
AC 自动机+dp。
题意
给定一个字符串序列和 \(n\) 不合法字串,求最少修改多少个字符能使得原序列中不包含不合法字串。
思路
类比一下本题的简化版(可以看看N总写的博客)。 在简化版中只有一个不合法字串。\(f[i][j]\) 定义为前 \(i\) 个字母走到了字串中的第 \(j\) 个位置的最少修改次数。
而本题中有多个不合法字串,那么就可以将 \(f[i][j]\) 定义为前 \(i\) 个字母走到了 AC 自动机中的第 \(j\) 个位置的最少修改次数。
首先将所有的不合法字串存入 Trie 中,并对每一个字串末尾的编号打上标记,表示不能匹配到这个位置。但是需要注意的是,如果当前节点的 \(next\) 数组指向的节点被打上标记,那么当前节点也要被打上标记。如下图所示:

那么就可以先循环原字符串的位置,再枚举已经走到的 AC 自动机中的节点编号,最内层循环下一个字符是什么,如果当前在 AC 自动机的节点往下一个字符走的节点被打上标记,那么就说明这种方案不合法,直接返回即可。如果合法,再判断当前节点是否和原字符串中的字符相同,进行状态转移。
最后再枚举 \(ans=\min(f[m][i])\)。其中 \(m\) 表示字符串的长度。如果还是无穷大就代表本题无解,直接返回 \(-1\) 即可。
code:
#include<cstdio>
#include<cstring>
using namespace std;
const int N=1010;
const int INF=0x3f3f3f3f;
char s[N];
int q[N],tr[N][4],f[N][N],ne[N],num,n,m;
bool tag[N];
int min(int a,int b){return a<b?a:b;}
int get(char c)
{
if(c=='A') return 0;
if(c=='G') return 1;
if(c=='C') return 2;
if(c=='T') return 3;
}
void init()
{
memset(tr,0,sizeof(tr));
memset(f,0x3f,sizeof(f));
memset(ne,0,sizeof(ne));
memset(tag,0,sizeof(tag));
num=0;
}
void insert()
{
int p=0;
for(int i=0;s[i];i++)
{
int v=get(s[i]);
if(!tr[p][v]) tr[p][v]=++num;
p=tr[p][v];
}
tag[p]=true;
}
void build_AC()
{
int hh=0,tt=-1;
for(int i=0;i<4;i++)
if(tr[0][i]) q[++tt]=tr[0][i];
while(hh<=tt)
{
int t=q[hh++];
for(int i=0;i<4;i++)
{
int c=tr[t][i];
if(!c) tr[t][i]=tr[ne[t]][i];
else
{
ne[c]=tr[ne[t]][i];
tag[c]|=tag[ne[c]];
q[++tt]=c;
}
}
}
}
int main()
{
int T=1;
while(scanf("%d",&n),n)
{
init();
while(n--)
{
scanf("%s",s);
insert();
}
build_AC();
scanf("%s",s+1);m=strlen(s+1);
f[0][0]=0;//别忘了初始化
for(int i=0;i<m;i++)
for(int j=0;j<=num;j++)
for(int k=0;k<4;k++)
{
int p=tr[j][k];
if(tag[p]) continue;
int t=get(s[i+1]);//注意这里要匹配的是下一个字符,不是当前字符
f[i+1][p]=min(f[i+1][p],f[i][j]+(t!=k));
}
int ans=INF;
for(int i=0;i<=num;i++) ans=min(ans,f[m][i]);
if(ans==INF) ans=-1;
printf("Case %d: %d\n",T++,ans);
}
return 0;
}
应用 [TJOI2013]单词
题意
给定 \(n\) 个单词,求每个单词在所有单词中出现了几次(包括本身)。
思路
看到题目是关于字符串的,同时又要求出现次数,那么显然就是 AC 自动机的题目。那么肯定要把所有的字符串先插入 Trie 中。
定义 \(f[i]\) 表示 Trie 中以编号 \(i\) 结尾的字串出现的次数(为了方便表示,下面的字符串 \(i\) 就代表 Trie 中以编号 \(i\) 结尾的字串),那么对于每一个单词,在插入的时候用 \(id\) 数组来记录该字串的末尾字符所对应的编号,最后的答案就是 \(f[id[i]]\)。
那么显然,如果字符串 \(i\) 出现过,那么与该字符串的后缀相匹配的字符串的前缀自然也就出现过。也就是字符串 \(ne[i],ne[ne[i]] \dots\)直到根节点为止都出现过。于是就得到了朴素的统计方法,对于 Trie 中的每一个字符,都做如下操作:
int p=c;
while(p)
{
cnt[p]++;
p=ne[p];
}
但是这样就妥妥 TLE 了。原因就在于,\(ne[p]\) 往上跳到根节点后,\(p\) 还要再通过 \(ne[p]\) 往上跳一次,这样的时间复杂度就很高了。
那么就可以考虑,首先令所有的 \(f[p]=1\),等更新完所有的 \(ne[p]\) 后,再从最后一层开始往上统计次数。那么此时就不能使用 \(while\) 循环了(因为用这个会一步搜到顶)。
于是就可以考虑用递推式求解,即:\(f[ne[i]]+=f[i]\)。原理就是因为字符串 \(ne[i]\) 肯定在字符串 \(i\) 出现时出现了。那么接下来的问题就是怎么在 \(O(n)\) 的时间内不重不漏地统计出所有 \(f[i]\)。
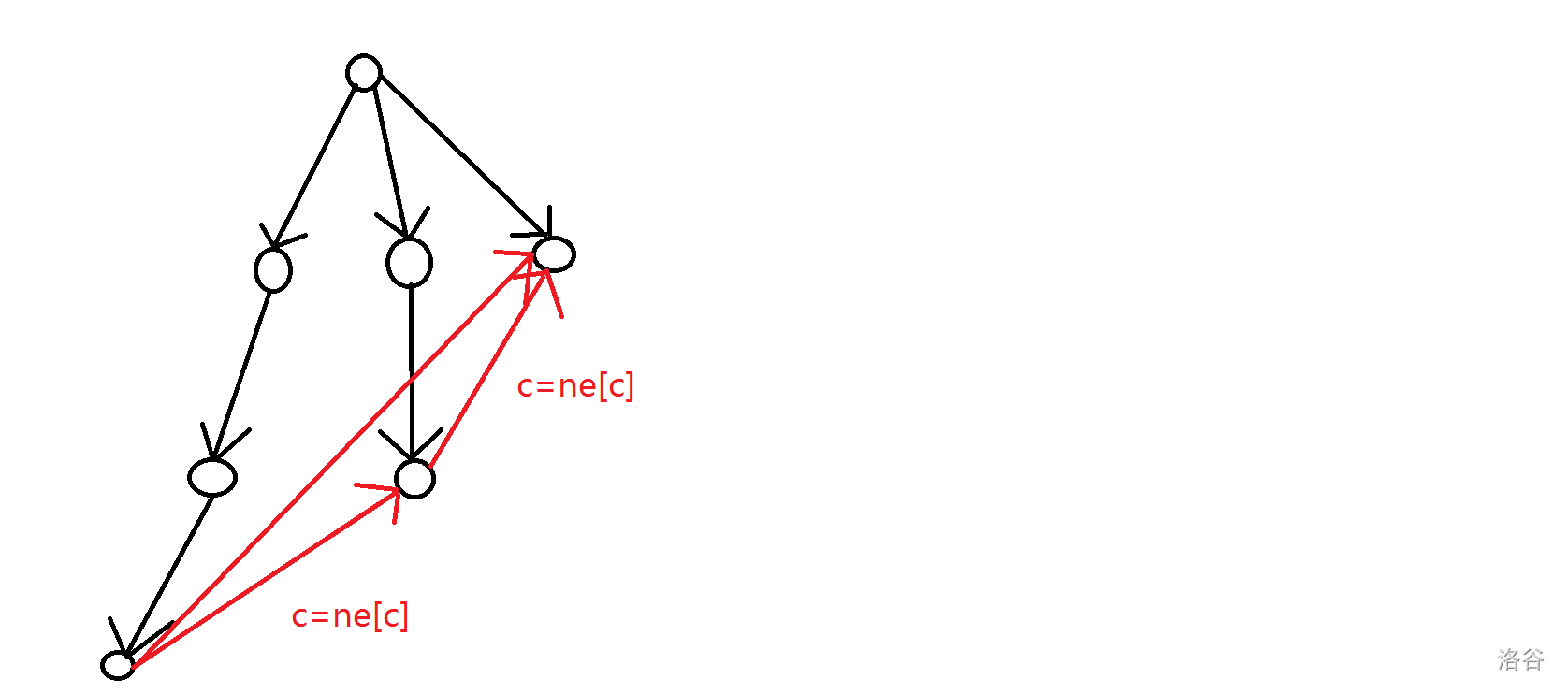
事实上,如果把所有字符串之间的递推关系看成是从 \(i\) 向 \(ne[i]\) 连一条边,那么最终就会构成一个图。同时由于最终 \(ne[i]\) 都会等于 \(0\)。所以这幅图实际上就是有向无环图,也就能构成一个拓扑序。那么按照拓扑序去递推 \(f[i]\) 就可以了。
接下来就是要统计每个点的入度来构造拓扑序吗?其实没必要,在 BFS 时的队列中储存的就是一个拓扑序的逆序。按照队列中的倒序递推就能得到最终答案。
code:
#include<cstdio>
using namespace std;
const int N=1e6+10;
int q[N],f[N],tr[N][26],num,n,ne[N];
char s[N];
int id[210];
void insert(int x)
{
int p=0;
for(int i=0;s[i];i++)
{
int t=s[i]-'a';
if(!tr[p][t]) tr[p][t]=++num;
p=tr[p][t];
f[p]++;//本身也出现了一次
}
id[x]=p;
}
void build_AC()
{
int hh=0,tt=-1;
for(int i=0;i<26;i++)
if(tr[0][i]) q[++tt]=tr[0][i];
while(hh<=tt)
{
int t=q[hh++];
for(int i=0;i<26;i++)
{
int c=tr[t][i];
if(!c) tr[t][i]=tr[ne[t]][i];
else
{
ne[c]=tr[ne[t]][i];
q[++tt]=c;
}
}
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%s",s),insert(i);
build_AC();
for(int i=num-1;i>=0;i--) f[ne[q[i]]]+=f[q[i]]; //根节点没有入队
for(int i=1;i<=n;i++) printf("%d\n",f[id[i]]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号