【洛谷】P7690 [CEOI2002] A decorative fence

题意

有 \(N\) 块长方形的木板，长度分别为 \(1,2,…,N\)，宽度都是 \(1\)。

现在要用这 \(N\) 块木板组成一个宽度为 \(N\) 的围栏，满足在围栏中，每块木板两侧的木板要么都比它高，要么都比它低。

也就是说，围栏中的木板是高低交错的。

我们称“两侧比它低的木板”处于高位，“两侧比它高的木板”处于低位。

显然，有很多种构建围栏的方案。

每个方案可以写作一个长度为 \(N\) 的序列，序列中的各元素是木板的长度。

把这些序列按照字典序排序，如下图所示，就是 \(N=4\) 时，所有满足条件的围栏按照木板长度的字典序排序后的结果。

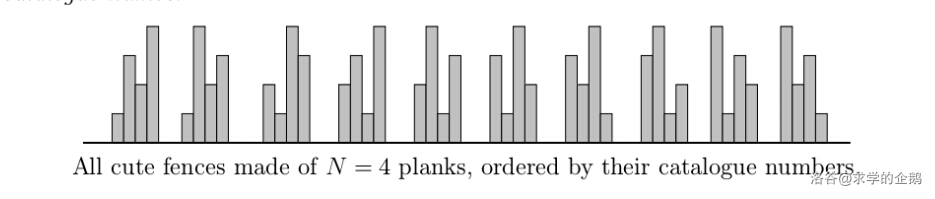
现在给定整数 \(C\)，求排名为 \(C\) 的围栏中，各木板的长度从左到右依次是多少。

数据范围

\(1 \leq N \leq 20\)，\(0 < C <2^{63}\)。

思路

思路来源于蓝书。

本题要求字典序排名为 \(C\) 的方案，而字典序的排序方式决定了本题可以采用试填法。具体地，第 \(i\) 个木板长度从小到大枚举到 \(j\) 时，第 \(i\) 位，固定填 \(j\)， \(i+1 \sim n\) 的所有填法数量大于等于要求的方案的排名 \(m\) ，那么答案中的第 \(i\) 位就必然是 \(j\)。考虑如何预处理出方案数。

定义 \(f[n][j][k]\) 表示用 \(n\) 块木板组成围栏，最左边的木板在这些木板中排名为 \(j\) （题目中隐含了每种长度只能用 \(1\) 次的条件），且最左边的木板状态为 \(k\) （\(k=0\) 表示低位，\(k=1\) 表示高位）的所有方案数。可以得到状态转移方程：

\(f[i][j][1]=\sum_{k=1}^{j-1} f[i-1][k][0]\)。

\(f[i][j][0]=\sum_{k=j}^{i-1} f[i-1][k][1]\)。

注意到第二个转移方程的 \(k \in[j,i-1]\)，这是因为 \(k\) 代表的是排名，而不是真实的长度，这里其实用到了离散的思想 (如对于 \(f[3][1][1]\)，\(1,3,2\) 和 \(4,7,5\) 在状态中都认为是 \(1,3,2\)，且只会被计算一次)。

接下来就考虑如何试填。由于题目中木板的长度是高低交替，于是可以先确定第一块木板的状态，再用一个数不断异或 \(1\) 来表示当前木板需要的状态。后面就可以从小到大枚举，依次确定每一块木板的长度，总复杂度为 \(O(N^2)\)，预处理的复杂度为 \(O(N^3)\)。

一些实现细节见代码。

code：

#include<cstdio>
#include<cstring>
using namespace std;
const int N=30;
#define int long long
int f[N][N][2],n,m,T;
bool vis[N];
void init()
{
	f[1][1][1]=f[1][1][0]=1;
	for(int i=2;i<=20;i++)
	    for(int j=1;j<=i;j++)
        {
	        for(int k=1;k<j;k++) f[i][j][1]+=f[i-1][k][0];
	        for(int k=j;k<i;k++) f[i][j][0]+=f[i-1][k][1];
		}
}
signed main()
{
	init();scanf("%lld",&T);
	while(T--)
	{
		scanf("%lld%lld",&n,&m);
		memset(vis,0,sizeof(vis));
		int last,k;
		for(int i=1;i<=n;i++)
		{
			if(f[n][i][1]>=m)//由于是按照字典序，所以优先考虑第二块木板最小的情况 
			{
				last=i,k=1;
				break;
			}
			else m-=f[n][i][1];//由于f[i][j][k] 表示的是方案数，而不是排名，所以需要减去字典序更小的方案数 
			if(f[n][i][0]>=m)
			{
				last=i,k=0;
				break;
			}
			else m-=f[n][i][0];
		}
		printf("%lld",last);vis[last]=true;
		for(int i=2;i<=n;i++)
		{
			k^=1;int rank=0;//rank 表示len在剩余没有选用的木板中排名rank,因为状态中需要用排名 
			for(int len=1;len<=n;len++)
			{
				if(vis[len]) continue;rank++;
				if(k==0&&len<last||k==1&&len>last)
                {
                	if(f[n-i+1][rank][k]>=m)
                	{
                		last=len;
                		break;
					}
					else m-=f[n-i+1][rank][k];
				}
			}
			vis[last]=true;//注意标记当前木板被使用过 
			printf(" %lld",last);
		}
		puts("");
	}
	return 0;
}