网络流学习笔记(二)——最小割
【最小割】模板
给定一个包含 \(n\) 个点 \(m\) 条边的有向图,并给定每条边的容量,边的容量非负。
图中可能存在重边和自环。求从点 \(S\) 到点 \(T\) 的最小割。
数据范围
\(2 \leq n \leq 10000,1 \leq m \leq 100000\)。
思路
根据最大流最小割定理,只需求出原图的最大流,即是原图的最小割。
code:
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int N=1e4+10;
const int M=2e5+10;
#define ll long long
const int INF=0x3f3f3f3f;
struct edge{
int v,w,nex;
}e[M];
int q[N],h[N],idx=1,n,m,s,t,d[N],cur[N];
void add(int u,int v,int w){e[++idx].v=v;e[idx].nex=h[u];e[idx].w=w;h[u]=idx;}
int min(int a,int b){return a<b?a:b;}
int max(int a,int b){return a>b?a:b;}
bool bfs() //构造分层图
{
int hh=0,tt=-1;
memset(d,-1,sizeof(d));
d[s]=0;q[++tt]=s;cur[s]=h[s];
while(hh<=tt)
{
int u=q[hh++];
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(d[v]==-1&&e[i].w)
{
d[v]=d[u]+1;
cur[v]=h[v];//当前弧优化
if(v==t) return true;
q[++tt]=v;
}
}
}
return false;
}
ll dfs(int u,int limit)//limit 是最大的容量
{
if(u==t) return limit;
ll flow=0;
for(int i=cur[u];i&&flow<limit;i=e[i].nex)//如果当前节点向子节点的流量已经超过了父节点最多传给它的流量,那么就没必要继续搜下去了
{
cur[u]=i;//如果遍历到了当前边,就说明前面的边都已经到了流量上限
int v=e[i].v;
if(d[v]==d[u]+1&&e[i].w)
{
ll t=dfs(v,min(e[i].w,limit-flow));
if(!t) d[v]=-1;//如果不能向子节点传输流量了,那么当前节点也就没有用了
e[i].w-=t,e[i^1].w+=t;flow+=t;
}
}
return flow;
}
ll Dinic()
{
ll res=0,flow;
while(bfs())
{
while(flow=dfs(s,INF)) res+=flow;//如果存在增广路径
}
return res;
}
int main()
{
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int u,v,w,i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&w);
add(u,v,w),add(v,u,0);
}
printf("%lld\n",Dinic());
return 0;
}
【应用】网络战争
给出一个带权无向图 \(G=(V,E)\),每条边 \(e\) 有一个权 \(w_e\)。
求将点 \(s\) 和点 \(t\) 分开的一个边割集 \(C\),使得该割集的平均边权最小,即最小化:
\(\dfrac{\sum_{e \in C} w_e}{|C|}\)。
注意: 本题边割集的定义与最小割中的割边的集合不同。在本题中,一个边割集是指:将这些边删去之后,\(s\) 与 \(t\) 不再连通。
数据范围
\(2≤n≤100,1≤m≤400\)。
思路
看到这个熟悉的分式自然就能想到 01 分数规划(可以先了解这个算法)。
将原图中的每条边的权值转化为 \(w_e-mid\)。由于本题是要求最小值,所以就是判断是否存在一种选法使得边权之和小于 \(0\)。
显然,转化后边权小于零的点一定会选。当然,小于零的实数也不能作为网络流中边的容量。
对于剩下的边集。如果题目是有向图,那么就可以根据最大流最小割定律直接上 Dinic。上面的题目已经提到过了如何处理无向边。这里就不再赘述了。经过转化之后也就可以上 Dinic 了。
code:
#include<cstdio>
#include<cstring>
using namespace std;
const int N=110;
const int M=810;
const double eps=1e-8;
const double INF=1e15;
int h[N],idx=1,n,m,s,t,cur[N],d[N],q[N];
struct edge{
int v,nex,f;
double w;
}e[M];
double min(double a,double b){return a<b?a:b;}
void add(int u,int v,int f){e[++idx].v=v;e[idx].f=f;e[idx].nex=h[u];h[u]=idx;}
bool bfs()
{
int hh=0,tt=-1;
memset(d,-1,sizeof(d));cur[s]=h[s];d[s]=0;q[++tt]=s;
while(hh<=tt)
{
int u=q[hh++];
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(d[v]==-1&&e[i].w)
{
d[v]=d[u]+1;cur[v]=h[v];
if(v==t) return true;
q[++tt]=v;
}
}
}
return false;
}
double dfs(int u,double limit)
{
if(u==t) return limit;
double flow=0;
for(int i=cur[u];i&&flow<limit;i=e[i].nex)
{
cur[u]=i;int v=e[i].v;
if(d[v]==d[u]+1&&e[i].w)
{
double t=dfs(v,min(limit-flow,e[i].w));
if(t==0) d[v]=-1;
flow+=t;e[i].w-=t;e[i^1].w+=t;
}
}
return flow;
}
bool check(double mid)
{
double res=0,flow;
for(int i=2;i<=idx;i+=2)
if(e[i].f*1.0<=mid)
{
e[i].w=e[i^1].w=0;
res+=e[i].f*1.0-mid;
}
else e[i].w=e[i^1].w=e[i].f*1.0-mid;
while(bfs()) while(flow=dfs(s,INF)) res+=flow;
return res<0.0;
}
int main()
{
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int u,v,f,i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&f);
add(u,v,f),add(v,u,f);
}
double l=0,r=1e7;
while(r-l>eps)
{
double mid=(l+r)/2.0;
if(check(mid)) r=mid;
else l=mid;
}
printf("%.2lf\n",r);
return 0;
}
【应用】最优标号
给定一个无向图 \(G=(V,E)\),每个顶点都有一个标号,它是一个 \([0,2^{31}-1]\) 内的整数。
不同的顶点可能会有相同的标号。
对每条边 \((u,v)\),我们定义其费用 \(cost(u,v)\) 为 \(u\) 的标号与 \(v\) 的标号的异或值。
现在我们知道一些顶点的标号。
你需要确定余下顶点的标号,使得所有边的费用和尽可能小。
数据范围
\(1≤N≤500,0≤M≤3000\)。
思路
看到题目是求异或的最小值,很容易就想到可以把原数的二进制下各个位分开来单独考虑(因为每个位的异或值互不影响)。
如果把二进制下第 \(i\) 位为 \(0\) 和为 \(1\) 的点分成两个集合,那么这一位对答案的贡献就是连接两个集合的边数。
发现什么了吗?割的定义和上面的思路很相似,那么就可以考虑把源点放在 \(0\) 集合中,把汇点放在 \(1\) 集合中。在不考虑已确定的数的情况下(虽然说如果所有数都可以自由搭配,那么答案就是 \(0\),这里是为了方便后面的描述),把每条边(无向边)的流量设为 \(1\),原问题就等价于求网络的最小割。
而有些点的值已经确定,那么就意味着这个点必然在一个确定的集合中,那么就可以将这个点和对应的源点(汇点)之间的边的流量设为 \(+\infty\)。再根据最大流最小割定理,求网络的最大流即可。
code:
#include<cstring>
#include<cstdio>
using namespace std;
const int N=1010;
const int M=10010;
const int INF=0x3f3f3f3f;
#define LL long long
struct edge{
int v,nex;
LL w;
}e[M];
struct edges{
int u,v;
}E[M];
int h[N],s,t,val[N],idx,n,m,cnt,cur[N],d[N],q[N];
LL min(LL a,LL b){return a<b?a:b;}
void add(int u,int v,LL w){e[++idx].v=v;e[idx].w=w;e[idx].nex=h[u];h[u]=idx;}
bool bfs()
{
int hh=0,tt=-1;
memset(d,-1,sizeof(d)); q[++tt]=s;cur[s]=h[s];d[s]=0;
while(hh<=tt)
{
int u=q[hh++];
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(d[v]==-1&&e[i].w)
{
d[v]=d[u]+1;cur[v]=h[v];
if(v==t) return true;
q[++tt]=v;
}
}
}
return false;
}
LL dfs(int u,LL limit)
{
if(u==t) return limit;
LL flow=0;
for(int i=cur[u];i&&flow<limit;i=e[i].nex)
{
cur[u]=i;int v=e[i].v;
if(d[v]==d[u]+1&&e[i].w)
{
int t=dfs(v,min(e[i].w,limit-flow));
if(!t) d[v]=-1;
flow+=t;e[i].w-=t;e[i^1].w+=t;
}
}
return flow;
}
void build_map(int k)
{
memset(h,0,sizeof(h));idx=1;
for(int i=1;i<=m;i++)
{
int u=E[i].u,v=E[i].v;
add(u,v,1),add(v,u,1);
}
for(int i=1;i<=n;i++)
if(val[i]>=0)
{
if((val[i]>>k)&1) add(s,i,INF),add(i,s,0);
else add(i,t,INF),add(t,i,0);
}
}
LL dinic(int k)
{
build_map(k);LL res=0,flow;
while(bfs())
{
while(flow=dfs(s,INF)) res+=flow;
}
return res;
}
int main()
{
scanf("%d%d",&n,&m);s=0,t=n+1;
for(int i=1;i<=m;i++) scanf("%d%d",&E[i].u,&E[i].v);
scanf("%d",&cnt);memset(val,-1,sizeof(val));
for(int u,v,i=1;i<=cnt;i++) scanf("%d%d",&u,&v),val[u]=v;
LL ans=0;
for(int i=0;i<=30;i++) ans+=(LL)dinic(i)<<i;
printf("%lld\n",ans);
}
最大权闭合子图
定义
对于一张有向图 \(G=(V,E)\),若存在一个点集 \(S\),所有以 \(S\) 内的点为入边的边的出边也都在 \(S\) 内,那么就称该点集为闭合子图。而使得点权之和最大的点集被称为最大闭合子图(点集当然不能包含所有的点)。
建图方式
记 \(w_i\) 为 \(i\) 的权值,原图中的所有点权为正数的点权之和为 \(tot\)。
从源点向所有点权为非负数的点连一条容量为 \(w_i\) 的边,从所有点权为负数的点向汇点连一条容量为 \(-w_i\) 的边,再把原图中的所有边的容量设成 \(+\infty\)。那么最大闭合子图的点权之和就是 \(tot-|f|\)。
证明
定义简单割为所有的割边必然与源点或汇点相连的割。
由于建图时把中间部分的边容量设为 \(+\infty\),而最大流的流量为 \(\sum_{u \in V}f(s,u)\),也必然为一个有限值。根据最大流最小割定理,最小割也就必然是一个简单割。
接下来证明闭合子图和简单割一一对应。
设原图中任意一个闭合子图的点集为 \(v'\),构造一个割集 \([S,T]\),其中 \(S=v'+s\),\(T=V-{S}\)。需要证明这个割集的所有割边都与源点或汇点相连。
由于 \(S\) 中除了源点以外的点构成一个闭合子图,故就无法通过中间的边走向 \(T\) (根据闭合子图的定义),那么中间的边就必然不是连接 \(S\) 和 \(T\) 的边,于是割边必然和源点或汇点相连。故任意一个闭合子图都可以对应一个简单割。
接下来证明割与闭合子图的权值之间存在确定的数量关系。
可以把网络中的所有点分成四部分:源点 \(s\),汇点 \(t\),闭合子图 \(v1\),闭合子图在原图中的补集 \(v1\)。那么就可以把割边分成从 \(s ->v2,v1->t\) 两类,如下图所示。
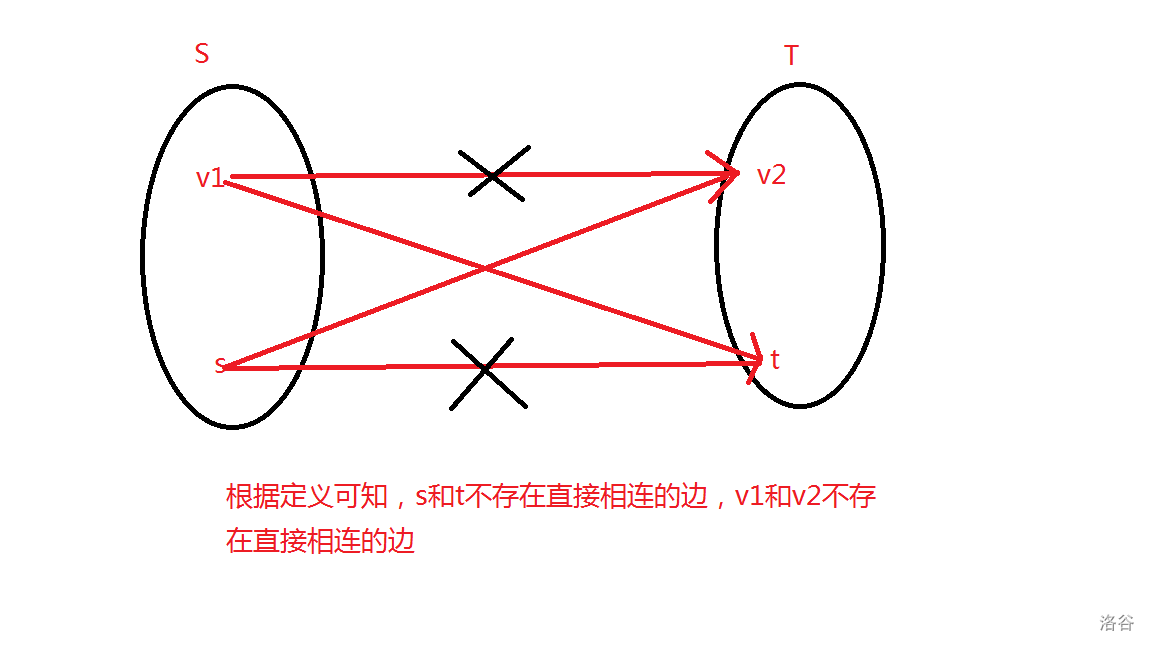
于是就可以得到割的容量的表达式:
\(c[S,T]=c[s,v2^{+}]+c[v1^{-},t]=\sum_{v \in v2^{+}}w_v+\sum_{v \in v1^{-}}-w_v\)。
(加上正负符号是因为要直接相连的边才算到总容量里面)
而原闭合子图的流量的表达式为:
\(w(v1)=\sum_{v \in v1^{+}}w_v-\sum_{v \in v1^{-}}-w_v\)。
两式相加,可以得到:
\(c[S,T]+w(v1)=\sum_{v \in v1^{+}}w_v+\sum_{v\in v2{+}}w_v=\sum_{v \in V^{+}}\)。
等式右边是原图中所有正权点的权值之和,为一个定值,故要使得 \(w(v1)\) 最大,就是要使得 \(c[S,T]\) 最小,那么也就是求网络的最小割。
【例题】[NOI2006] 最大获利
给定 \(N\) 个通讯站,建立第 \(i\) 个通讯站的花费为 \(p_i\)。
给定 \(M\) 个人群,满足第 \(i\) 个人群的需求需要建立 \(x1_i\) 和 \(x2_i\) 两个通讯站,收益为 \(c_i\)。
定义利润为所有满足人群的收益之和减去所有建立的通讯站的花费之和。求最大的利润。
数据范围
\(N≤5000,M \leq 50000\)。
思路
可以发现,如果从每个人群向所需的两个通讯站连有向边,并把通讯站的点权设为 \(-p_i\),那么原问题就转化为了求一个最大闭合子图。再根据上面提到的建图方式,求出最大流即可。
code:
#include<cstdio>
#include<cstring>
using namespace std;
const int N=1e5+10;
const int M=4e5+10;
const int INF=0x3f3f3f3f;
int h[N],idx=1,cur[N],n,m,d[N],q[N],s,t,tot;
struct edge{
int v,w,nex;
}e[M];
int min(int a,int b){return a<b?a:b;}
void add(int u,int v,int w){e[++idx].v=v;e[idx].w=w;e[idx].nex=h[u];h[u]=idx;}
bool bfs()
{
int hh=0,tt=-1;
memset(d,-1,sizeof(d));cur[s]=h[s];d[s]=0;q[++tt]=s;
while(hh<=tt)
{
int u=q[hh++];
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(d[v]==-1&&e[i].w)
{
d[v]=d[u]+1;cur[v]=h[v];
if(v==t) return true;
q[++tt]=v;
}
}
}
return false;
}
int dfs(int u,int limit)
{
if(u==t) return limit;
int flow=0;
for(int i=cur[u];i&&flow<limit;i=e[i].nex)
{
cur[u]=i;int v=e[i].v;
if(d[v]==d[u]+1&&e[i].w)
{
int t=dfs(v,min(limit-flow,e[i].w));
if(!t) d[v]=-1;flow+=t,e[i].w-=t;e[i^1].w+=t;
}
}
return flow;
}
int dinic()
{
int res=0,flow;
while(bfs())
{
while(flow=dfs(s,INF)) res+=flow;
}
return res;
}
int main()
{
scanf("%d%d",&n,&m);s=0,t=n+m+1;
for(int x,i=1;i<=n;i++) scanf("%d",&x),add(i+m,t,x),add(t,i+m,0);
for(int x,x1,x2,i=1;i<=m;i++)
{
scanf("%d%d%d",&x1,&x2,&x);
add(s,i,x),add(i,s,0);tot+=x;
add(i,x1+m,INF),add(x1+m,i,0);
add(i,x2+m,INF),add(x2+m,i,0);
}
printf("%d\n",tot-dinic());
}
最大密度子图
对于一个网络 \(G=(V,E)\),选择原图中的一个点集 \(v'\) 和一个边集 \(e'\),满足 \(\forall (a,b)\in e',a\in v',b \in v'\)。定义这种选法的密度为 \(\dfrac{|e'|}{|v'|}\)。使得密度最大的选法被称为原图的最大密度子图(密度子图为无向图)。
解法
看到最大化一个分式的值,就可以想到 \(0/1\) 分数规划模型。
那么就可以得到判断的不等式:
\(\dfrac{|e'|}{|v'|}>mid\)。
那么就可以将题意转化为求一种选法,使得 \(|e'|-|v'|*mid\) 最大。也就是使得 \(mid*|v'|-|e'|\) 最小。
设 \(v1\) 为 \(v'\) 在 \(V\) 下的补集。
考虑如何求出 \(|e'|\),可以发现,对于整张图,边数等于所有点的度数之和除以二。类比到子图上,也就是求出子图中所有点的度数之和,再减去割的容量,最后除以二,即可得到点数,即:
\(|e'|=\dfrac{1}{2}( \sum_{u \in v'} d_u-c[v',v1])\)。
也就可以推出:
\(|v'|*mid-|e'|=\sum_{u \in v'} mid-\dfrac{1}{2}( \sum_{u \in v'} d_u-c[v',v1])\)。
整理一下,可以得到:
\(|v'|*mid-|e'|=\dfrac{1}{2}( \sum_{u \in v'} (2*mid-d_u)+c[v',v1])\)。
但是这样还是无法直接求最小割来做,于是需要考虑一种特殊的构造方式,使得 \(|v'|*mid-|e'|\) 与 \(c[v',v1]\) 的有确定的数量关系。
事实上,在建图的时候将所有点向汇点连一条容量为 \(2*mid-d_u\) 的边,把原来所有的边的容量设为 \(1\),再从源点向所有点连一条边,由于 \(2*mid -d_u\) 可能是一个负数,所以需要将所有和源点或汇点边加上一个偏移量 \(delta\),那么从源点连出的边的容量就为 \(delta\)。
同时,也需要证明加上任意一个 \(delta\) 不会影响正确性,这里挖个坑,等着
N总 教我。
通过一系列的推导可以得到:
\(c[v',v1]=delta*n+2*mid*|v'|-2*|e'|\)。
最终要求的是 \(|e'|-|v'|*mid\) 的最大值,于是答案就是:
\((delta*n-c[v',v1])/2\)。
将这个式子和 \(0\) 比较一下即可继续二分答案。
【例题】Hard Life
给定一张 \(N\) 个点 \(M\) 条边无向图,求出图中至少包含一个点的密度最大的子图。输出方案。
数据范围
\(1≤n≤100,0≤m≤1000\)。
思路
直接按照求解最大密度子图的方法做这道题,对于最后输出的方案。通过上述的构造方式可以发现,最终在密度子图内的节点都可以通过源点直接到达;也可以回顾割的定义,在残留网络中从源点出发能够到达的点就是所选择的点。
code:
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int N=210;
const int M=11000;
const double eps=1e-8;
const double INF=1e10;
int h[N],idx=1,n,m,cur[N],q[N],d[N],s,t,ans,delta;
double din[N];
bool vis[N];
struct edges{
int u,v;
}E[M];
struct edge{
int v,nex;double w;
}e[M];
void add(int u,int v,double w){e[++idx].v=v;e[idx].w=w;e[idx].nex=h[u];h[u]=idx;}
bool bfs()
{
int hh=0,tt=-1;
memset(d,-1,sizeof(d));d[s]=0;cur[s]=h[s];q[++tt]=s;
while(hh<=tt)
{
int u=q[hh++];
// printf("%d ",u);
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(d[v]==-1&&e[i].w>0)
{
d[v]=d[u]+1;cur[v]=h[v];
if(v==t) return true;
q[++tt]=v;
}
}
}
// puts("");
return false;
}
double dfs(int u,double limit)
{
// printf("%d\n",t);
if(u==t) return limit;
double flow=0;
for(int i=cur[u];i&&flow<limit;i=e[i].nex)
{
int v=e[i].v;cur[u]=i;
if(d[v]==d[u]+1&&e[i].w>0)
{
double t=dfs(v,min(limit-flow,e[i].w));
if(t<=0) d[v]=-1;
e[i^1].w+=t;e[i].w-=t;flow+=t;
}
}
return flow;
}
void build_map(double mid)
{
memset(h,0,sizeof(h));idx=1;
for(int i=1;i<=m;i++)
{
int u=E[i].u,v=E[i].v;
add(u,v,1),add(v,u,1);
}
for(int i=1;i<=n;i++) add(s,i,delta),add(i,s,0),add(i,t,delta+2*mid-din[i]),add(t,i,0);
}
double dinic(double mid)
{
build_map(mid);
double res=0,flow;
while(bfs())
{
// puts("NLCAKIOI!!!");
while(flow=dfs(s,INF)) res+=flow;
}
// printf("%.10lf\n",res);
return res;
}
void dfs_nlc(int u)
{
vis[u]=true;ans+=(u!=s);
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(!vis[v]&&e[i].w>0) dfs_nlc(v);
}
}
int main()
{
scanf("%d%d",&n,&m);s=0,t=n+1;
for(int u,v,i=1;i<=m;i++) scanf("%d%d",&E[i].u,&E[i].v),din[E[i].u]++,din[E[i].v]++;
double l=0,r=m;delta=m;
while(r-l>eps)
{
double mid=(l+r)/2.0;
double tmp=dinic(mid);
if(n*delta-tmp>0) l=mid;
else r=mid;
}
dinic(l);
dfs_nlc(s);
if(!ans) printf("1\n1\n");
else
{
printf("%d\n",ans);
for(int i=1;i<=n;i++)
if(vis[i]) printf("%d\n",i);
}
return 0;
}
最小权点覆盖
定义
对于一张无向图,选出若干个点,使得每一条边连接的两个点都至少有一个点被选到,所选择的点集就被称为点覆盖集。而使得点集内的权值之和最小的点集就被称为最小权点覆盖集。
对于一般的图,最小权点覆盖问题是一个 NPC 问题。故接下来只会考虑二分图的最小权点覆盖集。
解法
如果每个点的权值都为 \(1\),那么根据二分图的经典结论:
二分图最大匹配 \(=\) 最小点覆盖数 \(=\) 点数 \(-\) 最大独立集数。
直接用匈牙利算法求解即可。
而对于一般的非负权值,就需要用网络流求解。
有一种很直观的想法,如果把最小权点覆盖问题转化为求网络的最小割,那么问题就迎刃而解了。
事实上,只需要从源点向左部节点 \(i\) 连一条容量为 \(w_i\) 的边;从右部节点 \(j\) 向汇点连一条容量为 \(w_j\) 的边。此时,如果割边是简单割,最小割的容量就是原图的最小权点覆盖,那么就需要将中间的边的容量设为正无穷。
接下来证明在这个网络中简单割和点权覆盖一一对应。
每个简单割都对应一个点权覆盖:
即证明,每一条边连接的点至少一个被选上。可以用反证法。假设一条边相连的两个点 \((i,j)\) 都没有被选。根据定义,即 \((s,i)\) 和 \((j,t)\) 都不是割边,而 \(c(i,j) = +\infty\),不会是割边。那么就存在一条从源点可以直达汇点的路径,这与割的定义矛盾。
每个点权覆盖都对应一个简单割:
此处不考虑存在冗余的点,因为要求的点权和最小,那么去掉冗余点后仍然正确,且点权和减小。要证明每个点权覆盖都对应一个简单割,即证明存在一种构造方法,使原网络变成一个简单割。
将所有连接被选择的左部点(右部点)和源点(汇点)之间的边删去,再从源点 DFS,能搜到的点在一个集合中,其余点在另外一个集合中。可以发现,对于这种构造方法,每条中间的边连接的左部点(右部点)与源点(汇点)之间必然有一条边被删去,那么就证明了这种构造方法形成的两个集合是一个割。而删去的边就是割边,故这又是一个简单割。而简单割的容量就是删去边的权值之和,也就是点集的权值之和。
【例题】Destroying The Graph
首先,爱丽丝绘制一个 \(N\) 个点 \(M\) 条边的有向图。
然后,鲍勃试图毁掉它。
在每一步操作中,鲍勃都可以选取一个点,并将所有射入该点的边移除或者将所有从该点射出的边移除。
已知,对于第 \(i\) 个点,将所有射入该点的边移除所需的花费为 \(W_{i}^{+}\),将所有从该点射出的边移除所需的花费为 \(W_i^{-}\)。
鲍勃需要将图中的所有边移除,并且还要使花费尽可能少。
请帮助鲍勃计算最少花费并输出方案。
数据范围
\(1≤N≤100,1≤M≤5000\)。
思路
注意到原题中给出的是一般的有向图,考虑将原图转化为二分图。
对于一条有向边 \((a,b)\),它要被删掉,那么就必然要进行 \(w_a^-\) 操作或 \(w_b^+\) 的其中之一。那么就特别像最小点权覆盖问题。于是就可以把每个点拆成两个点。再对于每条边 \((a,b)\),从 \(b^{+}\) 向 \(a^-\) 连一条边。
要求输出方案,其实和上一题的处理方法一样。唯一需要注意的是,上一题是输出点,这题实际上是输出边,所以处理方法略微不同。如果是在左部点就输出正号,在右部点就输出负号。
code:
#include<cstdio>
#include<cstring>
using namespace std;
const int N=210;
const int M=20010;
const int INF=0x3f3f3f3f;
int h[N],idx=1,n,m,d[N],q[N],cur[N],s,t,ans;
struct edge{
int v,w,nex;
}e[M];
bool vis[N];
void add(int u,int v,int w){e[++idx].v=v;e[idx].w=w;e[idx].nex=h[u];h[u]=idx;}
bool bfs()
{
int hh=0,tt=-1;memset(d,-1,sizeof(d));d[s]=0,cur[s]=h[s];q[++tt]=s;
while(hh<=tt)
{
int u=q[hh++];
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(d[v]==-1&&e[i].w)
{
d[v]=d[u]+1;cur[v]=h[v];
if(v==t) return true;
q[++tt]=v;
}
}
}
return false;
}
int min(int a,int b){return a<b?a:b;}
int find(int u,int limit)
{
if(u==t) return limit;
int flow=0;
for(int i=cur[u];i&&flow<limit;i=e[i].nex)
{
int v=e[i].v;cur[u]=i;
if(d[v]==d[u]+1&&e[i].w)
{
int t=find(v,min(e[i].w,limit-flow));
if(!t) d[v]=-1;flow+=t;e[i].w-=t;e[i^1].w+=t;
}
}
return flow;
}
void dfs(int u)
{
vis[u]=true;
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(!vis[v]&&e[i].w) dfs(v);
}
}
int dinic()
{
int res=0,flow;
while(bfs()) while(flow=find(s,INF)) res+=flow;
return res;
}
int main()
{
scanf("%d%d",&n,&m),s=0,t=2*n+1;
for(int w,i=1;i<=n;i++)
{
scanf("%d",&w);
add(s,i,w);add(i,s,0);
}
for(int w,i=1;i<=n;i++)
{
scanf("%d",&w);
add(i+n,t,w);add(t,i+n,0);
}
for(int u,v,i=1;i<=m;i++)
{
scanf("%d%d",&u,&v);
add(v,u+n,INF);add(u+n,v,0);
}
printf("%d\n",dinic());
dfs(s);
for(int i=2;i<idx;i+=2)
{
int u=e[i^1].v,v=e[i].v;
ans+=(vis[u]&&!vis[v]);
}
printf("%d\n",ans);
for(int i=2;i<idx;i+=2)
{
int u=e[i^1].v,v=e[i].v;
if(vis[u]&&!vis[v]&&u==s) printf("%d +\n",v);
}
for(int i=2;i<idx;i+=2)
{
int u=e[i^1].v,v=e[i].v;
if(vis[u]&&!vis[v]&&v==t) printf("%d -\n",u-n);
}
}
最大权独立集
类似于最小权覆盖集,与一般的二分图中的独立集的区别就在于加上了点权。
在一般的二分图(点权为 \(1\) )中,最大独立集 \(=\) 总点数 \(-\) 最小点覆盖集。
而在点权不一定为 \(1\) 的图中,上述的结论虽然不成立,但稍微更改仍然成立,即:
最大权独立集 \(=\) 总权值和 \(-\) 最小权覆盖集。
证明可以参考二分图中的证明方法,具体证明交给 N总。
【例题】王者之剑
给出一个 \(n \times m\) 网格,每个格子上有一个价值 \(v_{i,j}\) 的宝石。
Amber 可以自己决定起点,开始时刻为第 \(0\) 秒。
以下操作,在每秒内按顺序执行。
若第 \(i\) 秒开始时,Amber 在 \((x,y)\),则 Amber 可以拿走 \((x,y)\) 上的宝石。
在偶数秒时(\(i\) 为偶数),则 Amber 周围 \(4\) 格的宝石将会消失。
若第 \(i\) 秒开始时,Amber 在 \((x,y)\),则在第 \((i+1)\) 秒开始前,Amber 可以马上移动到相邻的格子 \((x+1,y),(x-1,y),(x,y+1),(x,y-1)\) 或原地不动 \((x,y)\)。
求 Amber 最多能得到多大总价值的宝石。
数据范围
\(1 \leq n,m \leq 100\)。
思路
首先可以推出本题的几个非常显然但很重要的性质:
1.只能在第偶数秒拿宝石,即第奇数秒到达的格子宝石一定已经消失或被拿走。
2.不可能同时拿走相邻格子上的宝石。
通过上面的性质,就可以发现本题的二分图模型,即把相邻的两个节点放在两个集合中。由于可以在原地停留,也就保证了这种建模方法的正确性。
于是只需根据最小权点覆盖问题的做法跑一遍网络流即可。
code:
#include<cstdio>
#include<cstring>
using namespace std;
const int N=10010;
const int M=60010;
const int INF=0x3f3f3f3f;
const int dx[4]={-1,1,0,0};
const int dy[4]={0,0,-1,1};
int h[N],idx=1,s,t,q[N],d[N],cur[N],n,m,tot;
struct edge{
int v,w,nex;
}e[M];
int min(int a,int b){return a<b?a:b;}
int get(int i,int j){return (i-1)*m+j;}
void add(int u,int v,int w){e[++idx].v=v;e[idx].w=w;e[idx].nex=h[u];h[u]=idx;}
bool bfs()
{
int hh=0,tt=-1;
memset(d,-1,sizeof(d));d[s]=0;q[++tt]=s;cur[s]=h[s];
while(hh<=tt)
{
int u=q[hh++];
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(d[v]==-1&&e[i].w)
{
d[v]=d[u]+1;cur[v]=h[v];
if(v==t) return true;
q[++tt]=v;
}
}
}
return false;
}
int dfs(int u,int limit)
{
if(u==t) return limit;
int flow=0;
for(int i=cur[u];i&&flow<limit;i=e[i].nex)
{
int v=e[i].v;cur[u]=i;
if(d[v]==d[u]+1&&e[i].w)
{
int t=dfs(v,min(e[i].w,limit-flow));
if(!t) d[v]=-1;e[i].w-=t;e[i^1].w+=t;flow+=t;
}
}
return flow;
}
int dinic()
{
int res=0,flow;
while(bfs()) while(flow=dfs(s,INF)) res+=flow;
return res;
}
bool check(int x,int y)
{
return x>=1&&x<=n&&y>=1&&y<=m;
}
int main()
{
scanf("%d%d",&n,&m);s=0,t=n*m+1;
for(int i=1;i<=n;i++)
for(int w,j=1;j<=m;j++)
{
scanf("%d",&w);tot+=w;
if((i+j)&1)
{
add(s,get(i,j),w),add(get(i,j),s,0);
for(int k=0;k<4;k++)
{
int x=i+dx[k],y=j+dy[k];
if(check(x,y)) add(get(i,j),get(x,y),INF),add(get(x,y),get(i,j),0);
}
}
else add(get(i,j),t,w),add(t,get(i,j),0);
}
printf("%d\n",tot-dinic());
}
【建模】有线电视网络
给定一张 \(n\) 个点 \(m\) 条边的无向图,求最少去掉多少个点,可以使图不连通。
如果不管去掉多少个点,都无法使原图不连通,则直接返回 \(n\)。
数据范围
$ 0≤n≤50$。
思路
其实本题的难点(毒瘤之处)在于输入格式。
看到使原图不连通,就可以想到最小割模型。那么本题的数据范围又非常小,于是就可以想到枚举源点和汇点。
但是注意到本题中删去的是点,而不是边。于是就可以想到拆点的技巧,即把每个点拆成入点和出点。同时原图中的边不能成为割边,于是就可以想到把所有原图中的边的容量设为正无穷。
接下来只需要枚举源点汇点,取最小割的最小值即可。
code:
#include<cstdio>
#include<cstring>
using namespace std;
const int N=1010;
const int M=10010;
const int INF=0x3f3f3f3f;
int h[N],idx=1,n,m,d[N],q[N],cur[N],s,t;
struct edge{
int v,w,nex;
}e[M];
int min(int a,int b){return a<b?a:b;}
void add(int u,int v,int w){e[++idx].v=v;e[idx].w=w;e[idx].nex=h[u];h[u]=idx;}
bool bfs()
{
int hh=0,tt=-1;
memset(d,-1,sizeof(d));d[s]=0,q[++tt]=s;cur[s]=h[s];
while(hh<=tt)
{
int u=q[hh++];
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(d[v]==-1&&e[i].w)
{
d[v]=d[u]+1;cur[v]=h[v];
if(v==t) return true;
q[++tt]=v;
}
}
}
return false;
}
int dfs(int u,int limit)
{
if(u==t) return limit;
int flow=0;
for(int i=h[u];i&&flow<limit;i=e[i].nex)
{
int v=e[i].v;cur[u]=i;
if(d[v]==d[u]+1&&e[i].w)
{
int t=dfs(v,min(e[i].w,limit-flow));
if(!t) d[v]=-1;e[i].w-=t;e[i^1].w+=t;flow+=t;
}
}
return flow;
}
int dinic()
{
int res=0,flow;
for(int i=2;i<=idx;i+=2) e[i].w+=e[i^1].w,e[i^1].w=0;
while(bfs()) while(flow=dfs(s,INF)) res+=flow;
return res;
}
int main()
{
while(scanf("%d%d",&n,&m)!=EOF)
{
memset(h,0,sizeof(h));idx=1;
for(int i=0;i<n;i++) add(i,i+n,1),add(i+n,i,0);
while(m--)
{
int a,b;
scanf(" (%d,%d)",&a,&b);
add(a+n,b,INF),add(b,a+n,0);
add(b+n,a,INF),add(a,b+n,0);
}
int res=n;
for(int i=0;i<n;i++)
for(int j=i+1;j<n;j++)
{
s=i+n,t=j;
res=min(res,dinic());
}
printf("%d\n",res);
}
return 0;
}
【建图】太空飞行计划问题
\(W\) 教授正在为国家航天中心计划一系列的太空飞行。
每次太空飞行可进行一系列商业性实验而获取利润。
现已确定了一个可供选择的实验集合 \(E={E_1,E_2,…,E_m}\) 和进行这些实验需要使用的全部仪器的集合 \(I={I_1,I_2,…,I_n}\)。
实验 \(E_j\) 需要用到的仪器是 \(I\) 的子集 \(R_j⊆I\)。
配置仪器 \(I_k\) 的费用为 \(c_k\) 美元。
实验 \(E_j\) 的赞助商已同意为该实验结果支付 \(p_j\) 美元。
\(W\) 教授的任务是找出一个有效算法,确定在一次太空飞行中要进行哪些实验并因此而配置哪些仪器才能使太空飞行的净收益最大。
数据范围
\(1≤n,m≤50\)
思路
可以发现,这其实就是最大获利那道题的拓展版,唯一的区别就在于本题的实验需要多个仪器,那么根据最大权闭合图的模型,直接建图求最大流即可。
code:
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int N=1e5+10;
const int M=4e5+10;
const int INF=0x3f3f3f3f;
int h[N],idx=1,cur[N],n,m,d[N],q[N],s,t,tot;
struct edge{
int v,w,nex;
}e[M];
bool vis[N];
int min(int a,int b){return a<b?a:b;}
void add(int u,int v,int w){e[++idx].v=v;e[idx].w=w;e[idx].nex=h[u];h[u]=idx;}
bool bfs()
{
int hh=0,tt=-1;
memset(d,-1,sizeof(d));cur[s]=h[s];d[s]=0;q[++tt]=s;
while(hh<=tt)
{
int u=q[hh++];
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(d[v]==-1&&e[i].w)
{
d[v]=d[u]+1;cur[v]=h[v];
if(v==t) return true;
q[++tt]=v;
}
}
}
return false;
}
int dfs(int u,int limit)
{
if(u==t) return limit;
int flow=0;
for(int i=cur[u];i&&flow<limit;i=e[i].nex)
{
cur[u]=i;int v=e[i].v;
if(d[v]==d[u]+1&&e[i].w)
{
int t=dfs(v,min(limit-flow,e[i].w));
if(!t) d[v]=-1;flow+=t,e[i].w-=t;e[i^1].w+=t;
}
}
return flow;
}
int dinic()
{
int res=0,flow;
while(bfs())
{
while(flow=dfs(s,INF)) res+=flow;
}
return res;
}
void dfs_nlc(int u)
{
vis[u]=true;
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(!vis[v]&&e[i].w) dfs_nlc(v);
}
}
int main()
{
// freopen("nlc.in","r",stdin);
// freopen("nlc.out","w",stdout);
scanf("%d%d",&m,&n);s=0,t=n+m+1;
for(int x,i=1;i<=m;i++)
{
scanf("%d",&x);tot+=x;
add(s,i,x);add(i,s,0);
char tools[10000];
memset(tools,0,sizeof tools);
cin.getline(tools,10000);
int ulen=0,tool;
while (sscanf(tools+ulen,"%d",&tool)==1)
{
add(i,tool+m,INF);add(tool+m,i,0);
if (tool==0)
ulen++;
else {
while (tool) {
tool/=10;
ulen++;
}
}
ulen++;
}
}
for(int x,i=1;i<=n;i++) scanf("%d",&x),add(i+m,t,x),add(t,i+m,0);
int res=tot-dinic();dfs_nlc(s);
for(int i=1;i<=m;i++) if(vis[i]) printf("%d ",i);
puts("");
for(int i=m+1;i<=n+m;i++) if(vis[i]) printf("%d ",i-m);
puts("");
printf("%d\n",res);
}
【建图】P3355 骑士共存问题
在一个 \(n \times n\) 个方格的国际象棋棋盘上,马(骑士)可以攻击的棋盘方格如图所示。
棋盘上某些方格设置了障碍,骑士不得进入。
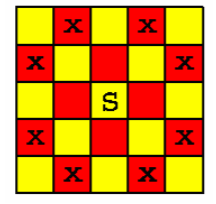
对于给定的 \(n \times n\) 个方格的国际象棋棋盘和障碍标志,计算棋盘上最多可以放置多少个骑士,使得它们彼此互不攻击。
数据范围
\(1 \leq n \leq 200\)。
思路
本题显然是一道二分图最大独立集问题。
只需对原棋盘按照马走的路径黑白染色。再根据:
最大独立集 \(=\) 总点数 \(-\) 最小点覆盖数,
直接跑网络流即可。
code:
#include<cstdio>
#include<cstring>
using namespace std;
const int N=40040;
const int M=4e5+10;
const int INF=0x3f3f3f3f;
const int dx[8]={-2,-2,-1,-1,1,1,2,2};
const int dy[8]={-1,1,-2,2,-2,2,-1,1};
int h[N],d[N],q[N],cur[N],s,t,n,m,idx=1;
bool bro[210][210];
struct edge{
int v,w,nex;
}e[M];
int min(int a,int b){return a<b?a:b;}
void add(int u,int v,int w){e[++idx].v=v;e[idx].w=w;e[idx].nex=h[u];h[u]=idx;}
bool bfs()
{
int hh=0,tt=-1;
memset(d,-1,sizeof(d));d[s]=0,q[++tt]=s;cur[s]=h[s];
while(hh<=tt)
{
int u=q[hh++];
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(d[v]==-1&&e[i].w)
{
d[v]=d[u]+1;cur[v]=h[v];
if(v==t) return true;
q[++tt]=v;
}
}
}
return false;
}
int dfs(int u,int limit)
{
if(u==t) return limit;
int flow=0;
for(int i=cur[u];i&&flow<limit;i=e[i].nex)
{
int v=e[i].v;cur[u]=i;
if(d[v]==d[u]+1&&e[i].w)
{
int t=dfs(v,min(e[i].w,limit-flow));
if(!t) d[v]=-1;e[i].w-=t;e[i^1].w+=t;flow+=t;
}
}
return flow;
}
int dinic()
{
int res=0,flow;
while(bfs()) while(flow=dfs(s,INF)) res+=flow;
return res;
}
int get(int i,int j){return (i-1)*n+j;}
int main()
{
scanf("%d%d",&n,&m);s=0,t=n*n+1;
for(int u,v,i=1;i<=m;i++) scanf("%d%d",&u,&v),bro[u][v]=true;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
if(bro[i][j]) continue;
if(i+j&1)
{
add(s,get(i,j),1);add(get(i,j),s,0);
for(int k=0;k<8;k++)
{
int x=i+dx[k],y=j+dy[k];
if(x<1||x>n||y<1||y>n||bro[x][y]) continue;
add(get(i,j),get(x,y),1);
add(get(x,y),get(i,j),0);
}
}
else add(get(i,j),t,1),add(t,get(i,j),0);
}
printf("%d\n",n*n-m-dinic());
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号