二分图学习笔记

N总认为我必须好好学习一下二分图，要不然过不了初赛。。。。。

二分图的定义

如果一张无向图的 $N$ 个节点（ $N \geq 2$）可以分成 $A,B$ 两个非空集合，其中 $A \cap B = \emptyset$。并且在同一集合内的点之间没有边相连，那么称这张无向图为一张二分图。

二分图判定

定理

一张图是二分图，当且仅当图中不存在长度为奇数的环（奇环）。

根据二分图的定义，一条边连接的两个点必定不在一个集合内，那么如果存在奇环，从环上任意一个点开始分到二分图重，那么最终会推到起始点即在 $A$ 集合中，又在 $B$ 集合中。故二分图中不存在奇环。

根据该定理，可以尝试用黑白染色法进行二分图的判定。也就是当一个节点被染色后，与他相连的所有点都要染成与它相反的颜色，如果发现一个节点要被染成两种颜色，则说明图中存在奇环。二分图染色法一般基于深度优先遍历实现，时间复杂度为 $O(n+m)$。

【例题】关押罪犯

给定一张 $n$ 个点 $m$ 条边的带权无向图，将这张图的每一个点分到两个集合的其中之一，求一种方案，使得连接同一个集合的两个点的边中，边权的最大值最小。

数据范围

$N \leq 20000,M \leq 100000$。

思路

看到边权最大值最小，就可以想到二分答案。看到将点分到两个集合，那么也就可以用黑白染色判定二分图来验证答案。

和普通的二分图不同，如果一条边的权值 $\leq mid$，那么它连接的两个顶点是可以在一个集合中的，那么也就只要对边权 $> mid$ 的边的两个顶点进行限制即可，如果一个顶点要被分到两个集合中，那么就说明原图不是二分图，令 $l=mid+1$；反之，则令 $r=mid$。

code:

#include<iostream>
//#include<nlcakioi>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=2e4+10;
const int M=2e5+10;
struct edge{
	int v,w,nex;
}e[M];
int h[N],idx,n,m,color[N];
void add(int u,int v,int w)
{
	e[++idx].v=v;
	e[idx].w=w;
	e[idx].nex=h[u];
	h[u]=idx;
}
bool dfs(int u,int col,int maxx)
{
	color[u]=col;
	for(int i=h[u];i;i=e[i].nex)
	{
		int v=e[i].v;
		if(e[i].w<=maxx) continue;
		if(color[v])
		{
			if(color[v]==col) return false;
		}
		else if(!dfs(v,3-col,maxx)) return false;
	}
	return true;
}
bool check(int k)
{
	memset(color,0,sizeof(color));
	for(int i=1;i<=n;i++)//图可能不连通，所以要枚举一遍所有的顶点
		if(color[i]==0)
			if(!dfs(i,1,k)) return false;	
    return true;
}
int main()
{   
//	while(1) puts("NLC&&CQY AK IOI!!!!!!!!!!!!");
    scanf("%d%d",&n,&m);
    for(int u,v,w,i=1;i<=m;i++)
    {
    	scanf("%d%d%d",&u,&v,&w);
    	add(u,v,w),add(v,u,w);
	}
	int l=0,r=1e9;
	while(l<r)
	{
		int mid=(l+r)>>1;
		if(check(mid)) r=mid;
		else l=mid+1;
	}
	printf("%d\n",r);
	return 0;
}

二分图最大匹配

“任意两条边都没有公共端点”的边的集合被称为图的一组匹配，在二分图中，包含边数最多的一组匹配被称为二分图的最大匹配。

对于任意一组匹配 $S$ （$S$ 是一个边集），属于 $S$ 的边被称为“匹配边”，不属于 $S$ 的边被称为“非匹配边”。匹配边的端点被称为“匹配点”，其他节点被称为“非匹配点”。如果在二分图中存在一条连接两个非匹配点的路径 $path$，使得非匹配边与匹配边在 $path$ 上交替出现，那么称 $path$ 是匹配 $S$ 的增广路，也称交错路。如下图所示：

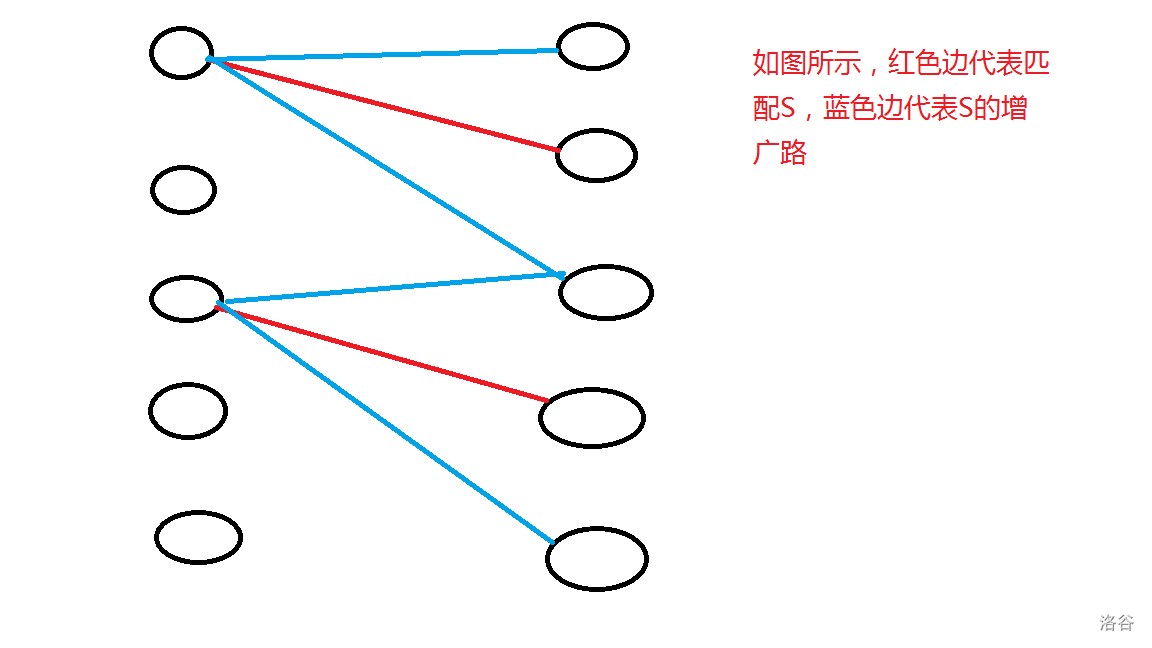
增广路具有以下性质：

1.长度 $len$ 是奇数（从上图中就可以看出）。

2.路径上第 $1,3,5,\dots,len$ 条边是非匹配边，第 $2,4,6,\dots,len-1$ 条边是匹配边。

从以上性质可以发现，如果将所有匹配边和非匹配边取反。那么原来的路径就成了原来增广路上的边集 $s'$ 的一条增广路。同时由于原增广路上的非匹配边比匹配边的数量多了 $1$，那么新的匹配就比原匹配的边数多了 $1$。显然原匹配就不可能是二分图的最大匹配。也就可以得到推论：

二分图的一组匹配 $S$ 是最大匹配，当且仅当图中不存在 $S$ 的增广路。

匈牙利算法（增广路算法）

匈牙利算法用于计算二分图的最大匹配。它的主要过程为：

1.设 $S= \emptyset$，即所有的边都是非匹配边。

2.寻找增广路 $path$，把路径上的所有边的匹配状态取反，得到一个更大的匹配 $S'$。

该算法的关键在于如何找到一条增广路。匈牙利算法依次尝试给每一个左部节点 $x$ 寻找一个匹配的右部节点 $y$。右部点 $y$ 能与左部点 $x$ 匹配，需要满足以下两个条件：

1.$y$ 本身就是非匹配点。此时无向边 $(x,y)$ 本身就是非匹配边，自己构成一条长度为 $1$ 的增广路。

2.$y$ 已经与左部点 $x'$ 匹配，但从 $x'$ 出发能到达另一个右部点 $y'$ 与之匹配。此时的路径 $x \sim y \sim x' \sim y'$ 为一条增广路。

在程序实现中，采用 DFS 的框架，递归地从 $x$ 出发寻找增广路。若找到，则在回溯时把路径上的匹配状态取反。同时也可以用一个全局变量记录节点的访问情况，避免重复搜索。（具体的递归过程可以参考这篇博客）

匈牙利算法的正确性基于贪心策略，它的一个重要特点是：当一个节点称为匹配点后，至多因为找到增广路而更换匹配对象，但是绝不会再变回非匹配点。

对于每个左部节点，寻找增广路最多遍历整张二分图一次。因此，匈牙利算法的理论时间复杂度为 $O(NM)$。但实际上的复杂度在随机数据中远低于理论复杂度。

code:

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int M=1e5+10;
const int N=520;
int match[N],h[N],idx,n1,n2,m;
bool st[N];
struct edge{
	int v,w,nex;
}e[M];
void add(int u,int v)
{
	e[++idx].v=v;
	e[idx].nex=h[u];
	h[u]=idx;
}
bool find(int u)
{
	for(int i=h[u];i;i=e[i].nex)
	{
		int v=e[i].v;
		if(!st[v])
		{
			st[v]=true;
			if(match[v]==0||find(match[v]))
			{
				match[v]=u;
				return true;
			}
		}
	}
	return false;
}
int main()
{       
	scanf("%d%d%d",&n1,&n2,&m);
	for(int u,v,i=1;i<=m;i++)
	{
		scanf("%d%d",&u,&v);
		add(u,v);
	}
	int res=0;
	for(int i=1;i<=n1;i++)
	{
		memset(st,false,sizeof(st));
		if(find(i)) res++;
	}
	printf("%d\n",res);
	return 0;
}

【例题】棋盘覆盖

给定一个 $N$ 行 $N$ 列的棋盘，有 $t$ 个格子禁止放置。

求最多能往棋盘上放多少块的长度为 $2$、宽度为 $1$ 的骨牌，骨牌的边界与格线重合（骨牌占用两个格子），并且任意两张骨牌都不重叠。

数据范围

$1\leq N,\leq 100$，$0 \leq t \leq100$。

思路

对原图构建出二分图匹配的模型。

二分图匹配模型有两个要素：

1.节点能分成独立的两个集合，每个集合内部有 $0$ 条边。

2.每个节点只能与 $1$ 条匹配边相连。

把这两个要素简称为 $0$ 要素和 $1$ 要素。

而在本题中，任意两张骨牌都不重叠，也就是每个格子只能被 $1$ 张骨牌覆盖（满足了 $0$ 要素）。而骨牌大小为 $1*2$，覆盖两个相邻的格子（满足了 $1$ 要素）。于是就可以在相邻两个非障碍物的格子之间连边。

如果把棋盘黑白染色（障碍物不染色，行数+列数为偶数的格子染成黑色，其余的格子染成白色），那么两个相同颜色的格子不可能被同一骨牌覆盖，也就是同色格子之间没有连边（$0$ 要素）。所有格子构成的图也就是一张二分图（根据二分图的定义），要求最大的骨牌数量，也就是求二分图最大匹配。

由于点数和边数都是 $N^2$ 级别的，故本题的时间复杂度就是 $O(N^4)$。

code：

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
#define PII pair<int,int> 
#define x first 
#define y second
const int N=110;
int dx[4]={-1,1,0,0};
int dy[4]={0,0,-1,1};
int n,m;
PII match[N][N];
bool g[N][N],st[N][N];
bool find(int x,int y)
{
	for(int i=0;i<4;i++)
	{
		int x1=x+dx[i];
		int y1=y+dy[i];
		if(x1<1||x1>n||y1<1||y1>n) continue;
		if(st[x1][y1]==true||g[x1][y1]==true) continue;
		st[x1][y1]=true;
		PII t=match[x1][y1];
		if(t.x==0||find(t.x,t.y))
	    {
	    	match[x1][y1]=make_pair(x,y);
	    	return true;
		}
	}
	return false;
}
int main()
{
    scanf("%d%d",&n,&m);
	for(int u,v,i=1;i<=m;i++)
	{
	    scanf("%d%d",&u,&v);
	    g[u][v]=true;
	}
	int res=0;
	for(int i=1;i<=n;i++)
	    for(int j=1;j<=n;j++)
	    {
	    	if((i+j)&1||g[i][j]) continue;
	    	memset(st,0,sizeof(st));
	    	if(find(i,j)) res++;
		}
	printf("%d\n",res);
	return 0;
}

【例题】車的放置

给定一个 $N$ 行 $M$ 列的棋盘，已知某些格子禁止放置。

问棋盘上最多能放多少个不能互相攻击的車。

車放在格子里，攻击范围与中国象棋的“車”一致。

数据范围

$1 \leq N,M \leq 200$

思路

本题和上一题类似。通过题意可以发现，每一行棋盘最多放一个“車”，每一列棋盘最多放一个“車”。那么就可以将每一行，每一列看成一个节点。在 $(i,j)$ 放置（前提是这个格子未被禁止放置）一个棋盘，就是在第 $i$ 行对应的节点与第 $j$ 列对应的节点之间连无向边。

由于每个“車”会连接一个行节点和一个列节点，所以行节点之间没有连边，列节点同理。故本题的图是一张二分图。放置一个“車”就是将一个行节点和一个列节点进行匹配。故只需求一下二分图的最大匹配即可。时间复杂度为 $O((N+M)NM)$。

code：

#include<cstdio>
#include<cstring>
using namespace std;
const int N=210;
int n,m,t,res,h[N],idx;
bool g[N][N],st[N];
int match[N];
bool find(int u)
{
	for(int i=1;i<=m;i++)
	{
	    if(st[i]||g[u][i]) continue;
		st[i]=true;
		if(!match[i]||find(match[i]))	
		{
			match[i]=u;
			return true;
		}
	}
	return false;
}
int main()
{
	scanf("%d%d%d",&n,&m,&t);
	for(int x,y,i=1;i<=t;i++)
	{
		scanf("%d%d",&x,&y);
		g[x][y]=true;
	}    
	for(int i=1;i<=n;i++)
	{
	    memset(st,0,sizeof(st));
	    if(find(i)) res++;
	}
	printf("%d\n",res);
	return 0;
}

完备匹配

给定一张二分图，其左部、右部节点数量均为 $N$。如果该二分图的最大匹配包含 $N$ 条匹配边，则称该二分图具有完备匹配。

多重匹配

给定一张包含 $N$ 个左部节点、$M$ 个右部节点的二分图。从中选出尽量多的边，使第 $i(1 \leq i \leq N)$ 个左部节点至多与 $kl_i$ 条选出的边相连，第 $j(1 \leq j \leq N)$ 个右部节点至多与 $kr_j$ 条选出的边相连。该问题被称为二分图的多重匹配。

当 $kl_i=kr_j=1$ 时，上述问题就简化为二分图最大匹配。因此，多重匹配时一个广义的“匹配”问题，每个节点可以与不止一条“匹配”边相连，但不能超过一个给定的限制。

多重匹配一般有四种解决方案：

1.拆点。把第 $i$ 个左部节点拆成 $kl_i$ 个不同的左部节点，第 $j$ 个右部节点拆成 $kr_j$ 个不同的右部节点。对于原图中的每条边 $(i,j)$，在 $i$ 拆成的所有节点与 $j$ 拆成的所有节点之间连边。然后求二分图最大匹配。

2.如果所有的 $kl_i=1$ 或者所有的 $kr_j=1$，即只有一侧是多重匹配。设左部是“多重”的，那么直接在匈牙利算法中让每个左部节点执行 $k_l$ 次 dfs 即可。

3.在第二种方案中，如果设右部是多重的，那么就可以让每一个右部节点可以匹配 $kr_j$ 次，超过匹配次数后，再进行递归。

4.网络流。但是本蒟蒻不会，需要请教 N总。

二分图带权匹配

给定一张二分图，二分图的每条边都带有一个权值。求出该二分图的一组最大匹配，使得匹配变的权值总和最大。注意，二分图带权最大匹配的前提是匹配数最大。然后再最大化匹配变的权值总和。

二分图带权最大匹配有两种解法：费用流和 KM 算法。不过蒟蒻太菜了，所以费用流求解需要请教 N总。KM 算法在稠密图上的效率一般高于费用流。不过，KM 算法有很大的局限性，只能在满足“带权最大匹配一定是完备匹配”的图中正确求解。

以下关于 KM 算法的内容均设二分图的左、右两部的节点数都是 $N$。

交错树

在匈牙利算法中，如果从某个左部节点出发寻找匹配失败，那么在 DFS 的过程中，所有访问过的节点，以及为了访问这些节点而经过的边，共同构成一棵树。

这棵树的根节点是一个左部节点，所有叶子节点也都是左部节点（因为最终匹配失败了），并且树上第 $1,3,5 \dots$ 层的边都是非匹配边，第 $2,4,6 \dots$ 层的边都是匹配边。因此，这棵树被称为交错树。

顶标（顶点标记值）

在二分图中，给第 $i$ 个左部节点一个整数值 $A_i$，给第 $j$ 个右部节点一个整数值 $B_j$。同时，必须满足 $\forall i,j,A_i+B_j \geq w(i,j)$。其中 $w(i,j)$ 表示第 $i$ 个左部节点与第 $j$ 个右部节点之间的边权（没有边时设为负无穷）。这些整数值 $A_i,B_j$ 称为节点的顶标。

相等子图

二分图中所有的节点和满足 $A_i+B_j=w(i,j)$ 的边构成的子图，称为二分图的相等子图，边被称为相等边。

定理

若相等子图中存在完备匹配，则这个完备匹配就是二分图的最大带权匹配。

证明：

在相等子图中，完备匹配的边权和等于 $\sum_{i=1}^{N}A_i+\sum_{i=1}^{N}B_i$，即所有顶标之和。

因为顶标满足 $\forall i,j,A_i+B_j \geq w(i,j)$。所以在整个二分图中，任何一组匹配的边权之和都不可能大于所有的顶标之和。

证毕。

KM 算法的基本思想就是，先在满足 $\forall i,j,A_i+B_j \geq w(i,j)$ 的前提下，给每个节点随机赋值一个顶标，然后采取适当的策略不断扩大相等子图的规模，直至相等子图存在完备匹配。例如，可以赋值 $A_i=\max_{1 \leq j \leq N}{w(i,j)},B_j=0$。

对于一个相等子图，用匈牙利算法求它的最大匹配。若最大匹配不完备，则说明一定有一个左部节点匹配失败。该节点匹配失败的那次 DFS 形成了一棵交错树，记为 $T$。

考虑匈牙利算法的流程，容易发现以下两条结论：

1.除了根节点以外，$T$ 中其他的左部点都是从右部节点沿着匹配边访问到的，即在程序中调用了 $dfs(match[y])$，其中 $y$ 是一个右部节点。

2.$T$ 中所有的右部点都是从左部点沿着非匹配边访问到的。

在寻找增广路以前，不会改变已有的匹配，所以一个右部节点沿着匹配边能访问到的左部节点是固定的。为了让匹配数增加，我们只能从第 $2$ 条结论入手，考虑“怎样能让左部点沿着非匹配边访问到更多的右部点”。

假设把 $T$ 中所有的左部节点顶标 $A_i(i \in T)$ 减小一个整数值 $\Delta$，把 $T$ 所有的右部节点顶标 $B_j(j \in T)$ 增大一个整数值 $\Delta$，节点的访问情况就会发生变化，分两方面进行讨论：

1.右部点 $j$ 沿着匹配边，递归访问 $match[j]$。对于一条匹配边，显然要么 $i,j \in T$（被访问到），要么 $i,j \notin T$。故 $A_i+B_j$ 不变，匹配边仍然属于相等子图。

2.左部节点 $i$ 沿着非匹配边，访问右部节点 $j$，尝试与之匹配。因为左部节点的访问是被动的（被右部节点沿着匹配边递归），所以 $i$ 始终在 $T$ 当中，只需考虑 $i \in T$。

(1) 若 $i,j \in T$，则 $A_i+B_j$ 不变。即以前能从 $i$ 访问到的点 $j$，现在仍然能访问。

(2) 若 $i \in T,j \notin T$，则 $A_i+B_j$ 减小。即以前从 $i$ 访问不到的节点 $j$，现在有可能访问到了。

为了保证顶标符合前提条件 $\forall i,j,A_i+B_j \geq w(i,j)$，我们就在所有 $i \in T,j \notin T$ 的边 $(i,j)$ 中，找出最小的 $A_i+B_j-w(i,j)$，作为 $\Delta$ 的值。只要原图中存在完备匹配，这样的边一定存在。上述方法既不会破坏前提条件，又能保证至少有一条新的边会加入相等子图（根据上面的讨论以及构造方法），使交错树中至少一个左部节点能访问到的右部节点增多。

不断重复以上过程，直到每一个左部点都匹配成功，就得到了相等子图的完备匹配，即原图的带权最大匹配。时间复杂度为 $O(N^4)$，在随机数据中为 $O(N^3)$。

code：

#include<cstdio>
#include<cstring>
using namespace std;
const int N=510;
const bool NLCAKIOI=true;
#define int long long 
const int INF=1e15;
int w[N][N],match[N]; 
int la[N],lb[N];//顶标
bool va[N],vb[N];//是否在交错树中
int n,m,delta,upd[N];//更新顶标
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
bool find(int u)
{
	va[u]=true;
	for(int v=1;v<=n;v++)
	{
		if(!vb[v]&&w[u][v]!=INF)
		{
			if(la[u]+lb[v]==w[u][v])
			{
				vb[v]=true;
				if(!match[v]||find(match[v]))
				{
					match[v]=u;
					return true;
				}
			}
			else upd[v]=min(upd[v],la[u]+lb[v]-w[u][v]);
		} 
	} 
	return false;
} 
void KM()
{
	for(int i=1;i<=n;i++)
	{
		la[i]=-INF;lb[i]=0;
		for(int j=1;j<=n;j++)
		    if(w[i][j]!=INF) la[i]=max(la[i],w[i][j]);
	}
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		while(NLCAKIOI)
	    {
	    	memset(va,0,sizeof(va));
	    	memset(vb,0,sizeof(vb));
	    	for(int j=1;j<=n;j++) upd[j]=INF;
	    	if(find(i)) break;
            delta=INF;
	    	for(int j=1;j<=n;j++) delta=min(delta,upd[j]);
	    	for(int j=1;j<=n;j++)
	    	{
	    		if(va[j]) la[j]-=delta;
	    		if(vb[j]) lb[j]+=delta;
			}
		}
	}
	for(int i=1;i<=n;i++) ans+=w[match[i]][i];
	printf("%lld\n",ans);
	for(int i=1;i<=n;i++) printf("%lld ",match[i]);
	puts("");   
}
signed main()
{
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=n;i++)
	    for(int j=1;j<=n;j++)
	        w[i][j]=INF;
	for(int u,v,W,i=1;i<=m;i++)
	{
	    scanf("%lld%lld%lld",&u,&v,&W);
		w[u][v]=W;	
	}
	KM();
	return 0;
}

但是如果把这道题交到KM 算法的模板题后会发现，有一半的点 TLE。

这是因为模板题中 $n \leq 500$，并且数据并不是随机生成的，这使得朴素的 KM 算法的时间复杂度会降到 $O(N^4)$，需要考虑将算法优化成在任何数据下的复杂度都是 $O(N^3)$。

注意到每次修改顶标值时，都会重新遍历一遍原交错树，但通过上面的分析可以发现，每次修改顶标值时，交错树内部的结构并没有改变，且新的点都是在原来的叶子节点上拓展。而根据构造 $\Delta$ 的方式，每次都会至少有一个新的拓展点，所以匹配失败时只需要在这个指定的拓展点进行拓展就好了。也就是匈牙利算法递归的过程改成 BFS。

code：

#include<cstdio>
#include<cstring>
using namespace std;
const int N=510;
const bool NLCAKIOI=true;
#define int long long 
const int INF=1e10;
int w[N][N],match[N];
int p[N];//用于记录交错树,p[i]表示i的祖先 
int la[N],lb[N];//顶标
bool va[N],vb[N];//是否在交错树中
int n,m,delta,upd[N];//更新顶标
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
void bfs(int now)
{
	int v=0,v1=0;
	for(int i=1;i<=n;i++) p[i]=0,upd[i]=INF;
	match[0]=now; //这样写便于更新 
	do{
		int u=match[v],delta=INF;vb[v]=true;
		for(int i=1;i<=n;i++)//实际上这里的边都不在交错树中，所以在更新delta值前不存在相等边 
		{
			if(vb[i]) continue;
			if(upd[i]>la[u]+lb[i]-w[u][i])	upd[i]=la[u]+lb[i]-w[u][i],p[i]=v;//可能的方向：v->u->i 
			if(upd[i]<delta) delta=upd[i],v1=i;//拓展的点 
		}
		for(int i=0;i<=n;i++)
		{
			if(vb[i]) la[match[i]]-=delta,lb[i]+=delta;
			else upd[i]-=delta;
		}
		v=v1;
	} while(match[v]);
    while(v) match[v]=match[p[v]],v=p[v];
}
void KM()
{
	for(int i=1;i<=n;i++)
	{
	    memset(vb,0,sizeof(vb));
	    bfs(i);
	}
	int ans=0;
	for(int i=1;i<=n;i++) ans+=w[match[i]][i];
	printf("%lld\n",ans);
	for(int i=1;i<=n;i++) printf("%lld ",match[i]);
	puts("");   
}
signed main()
{
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=n;i++)
	    for(int j=1;j<=n;j++)
	        w[i][j]=-INF;
	for(int u,v,W,i=1;i<=m;i++)
	{
	    scanf("%lld%lld%lld",&u,&v,&W);
		w[u][v]=W;	
	}
	KM();
	return 0;
}

【例题】Ants

平面上共有 $2 \times N$ 个点，$N$ 个是白点，$N$ 个是黑点。对于每一个白点，找到一个黑点，把二者用线段连起来，要求最后所有线段都不相交，求一种方案，保证有解。

数据范围

$N \leq 100$。

思路

如果第 $i_1$ 个白点连第 $j_1$ 个黑点，第 $i_2$ 个白点连第 $j_2$ 个黑点，并且线段 $(i_1,j_1)$ 与 $(i_2,j_2)$ 相交，那么交换一下，让 $i_1$ 连 $j_2$，让 $i_2$ 连 $j_1$，这样就不会交叉。并且由三角形两边之和大于第三边可知，两条线段的长度之和一定变小，如下图所示：

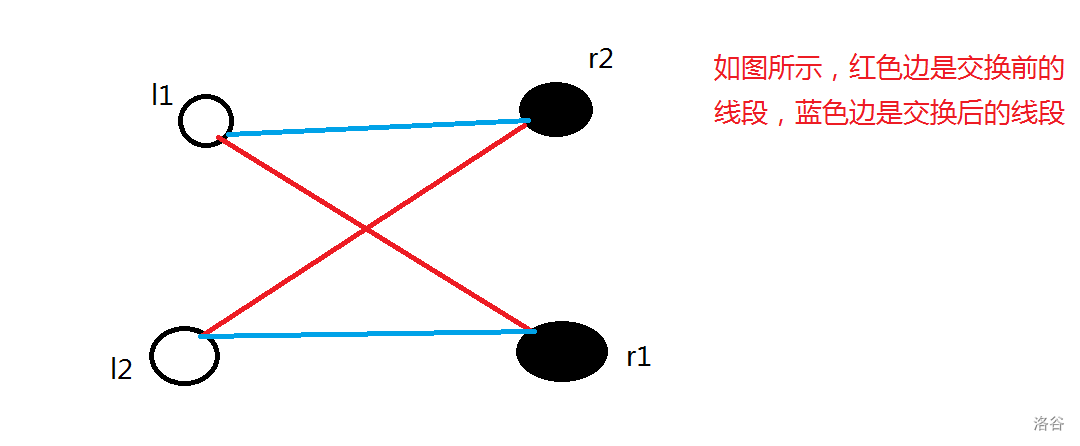
故本题等价于让每条线段的长度之和最小。

那么就可以在每个白点和黑点之间连一条边，边权为它们距离的相反数，再用 KM 算法求带权最大匹配即可。

看了 lydrainbowcat的讲解以后发现，上面提到的 $O(N^3)$ 的 KM 算法实际上还是一个 DFS。所以下面的代码采用 lyd 老师的 DFS 写法。

code:

#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
using namespace std;
const int N=110;
const double INF=1e20;
const double eps=1e-10;
double w[N][N];
int match[N],last[N];
double la[N],lb[N],delta,upd[N];
bool va[N],vb[N];
int n,m;
struct points{
	int x,y;
}a[N],b[N];
double get_dis(int i,int j)
{
	double x1=a[i].x-b[j].x,y1=a[i].y-b[j].y;
	return sqrt(x1*x1+y1*y1);
}
bool find(int u,int fa)
{
	va[u]=true;
	for(int v=1;v<=n;v++)
	{
		if(!vb[v])
		{
			if(fabs(la[u]+lb[v]-w[u][v])<eps)
			{
				vb[v]=true;last[v]=fa;
				if(!match[v]||find(match[v],v))
				{
					match[v]=u;
					return true;
				}
			}
			else if(upd[v]>la[u]+lb[v]-w[u][v]+eps)
			{
				upd[v]=la[u]+lb[v]-w[u][v]+eps;
				last[v]=fa;
			}
		} 
	} 
	return false;
} 
void KM()
{
	memset(match,0,sizeof(match));
	for (int i=1;i<=n;i++)
	{
        la[i]=-INF;lb[i]=0;
        for(int j=1;j<=n;j++) la[i]=max(la[i],w[i][j]);
    }
	for(int i=1;i<=n;i++)
	{
	    memset(vb,0,sizeof(vb));
	    memset(va,0,sizeof(va));
	    for(int j=1;j<=n;j++) upd[j]=INF;
	    int now=0;match[0]=i;
	    while(match[now])
	    {
	    	double delta=INF;
	    	if(find(match[now],now)) break;
	    	for(int j=1;j<=n;j++)
	    	{
	    		if(!vb[j]&&delta>upd[j])
	    		{
	    			delta=upd[j];
	    			now=j;
				}
			}
			for(int j=1;j<=n;j++)
			{
				if(va[j]) la[j]-=delta;
				if(vb[j]) lb[j]+=delta;
				else upd[j]-=delta;
			}
			vb[now]=true;
		}
		while(now) match[now]=match[last[now]],now=last[now]; 
	}
	for(int i=1;i<=n;i++) printf("%d\n",match[i]);
}
signed main()
{
	while(scanf("%d",&n)!=EOF)
	{
	    for(int i=1;i<=n;i++) scanf("%d%d",&b[i].x,&b[i].y);
		for(int i=1;i<=n;i++) scanf("%d%d",&a[i].x,&a[i].y);
		for(int i=1;i<=n;i++)
		    for(int j=1;j<=n;j++)
		        w[i][j]=-get_dis(i,j);
		KM();
	} 
	return 0;
}

二分图最小点覆盖

给定一张二分图，求出一个最小的点集 $S$，使得图中任意一条边都有至少一个端点属于 $S$。这个问题被称为二分图的最小点覆盖，简称最小覆盖。

König 定理

二分图最小点覆盖包含的点数等于二分图最大匹配包含的边数。

证明：

首先，因为最大匹配是原二分图边集的一个子集，并且所有边都不相交，所以至少需要从每条匹配边中选出一个端点。因此，最小点覆盖包含的点数不可能小于最大匹配包含的边数。如果能对任意二分图构造出一组覆盖点，其包含的点数等于最大匹配包含的边数，
那么定理就能得证。构造方法如下：

1.求出二分图的最大匹配

2.从左部每个非匹配点出发，再执行一次 DFS 寻找增广路的路径（必然失败），标记访问过的节点。

3.取左部未被标记的点，右部被标记的点，就得到了二分图的最小点覆盖。

下证该构造方法的正确性。

经过上述构造方法后：

1.左部非匹配点一定都被标记——因为它们是出发点。

2.右部非匹配点一定都没有被标记——否则就找到了增广路。

3.一对匹配点要么都被标记，要么都没被标记——因为在寻找增广路过程中，左部匹配点都只能通过右部到达。

在构造中，我们取了左部未被标记的点、右部被标记的点。根据上面的讨论可以发现，恰好是每条匹配边选取了一个点，所以选出的点数等于最大匹配边数。

再来讨论这种取法是否覆盖了所有的边：

1.匹配边一定被覆盖——因为恰好有一个端点被取走。

2.不存在连接两个非匹配点的边——否则就有长度为 $1$ 的增广路了。

3.连接左部非匹配点 $i$ 和右部匹配点 $j$ 的边——因为 $i$ 是出发点，所以 $j$ 一定被访问，而我们取了右部所有被标记的点，因此这样的边也被覆盖。

4.连接左部匹配点 $i$ 和右部非匹配点 $j$ 的边——$i$ 一定没有被访问，否则再走到 $j$ 就形成了增广路。而我们取了左部所有未被标记的点，因此这样的边也被覆盖。

证毕。

【例题】机器任务

有两台机器 $A$，$B$ 以及 $K$ 个任务。

机器 $A$ 有 $N$ 种不同的模式（模式 $0 \sim N-1$），机器 $B$ 有 $M$ 种不同的模式（模式 $0 \sim M-1$）。

两台机器最开始都处于模式 $0$。

每个任务既可以在 $A$ 上执行，也可以在 $B$ 上执行。

对于每个任务 $i$，给定两个整数 $a[i]$ 和 $b[i]$，表示如果该任务在 $A$ 上执行，需要设置模式为 $a[i]$，如果在 $B$ 上执行，需要模式为 $b[i]$。

任务可以以任意顺序被执行，但每台机器转换一次模式就要重启一次。

求怎样分配任务并合理安排顺序，能使机器重启次数最少。

数据范围

$N,M<100,K<1000$

$ 0 \leq a[i]< N$

$0 \leq b[i]<M$

思路

二分图最小覆盖的模型特点是：每条边有两个端点。二者至少选择一个。称之为 2 要素。如果一个题目具有 $2$ 要素的特点，那么可以抽象成二分图最小覆盖模型求解。

本题中的任务 $i$ 要么在机器 $A$ 上以 $A[i]$ 模式执行，要么在机器 $B$ 上以 $B[i]$ 模式执行。因此，可以把 $A$ 的模式抽象成左部点， $B$ 的模式抽象成右部点。每个任务作为无向边。那么显然形成了一张二分图。题意是要求最少的模式完成所有任务，在二分图中就转化为了求图中的最小点覆盖。

根据 König 定理，直接用匈牙利算法求出最大匹配数即可。时间复杂度为 $O(NM)$。

code：

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=110;
int n,m,k;
bool g[N][N],st[N];
int match[N];
bool find(int u)
{
	for(int i=1;i<m;i++)
	{
		if(st[i]||!g[u][i]) continue;
		st[i]=true;
		int t=match[i];
		if(!t||find(t))
		{
			match[i]=u;
			return true;
		}
	}
	return false;
}
int main()
{
	while(scanf("%d",&n))
	{
		if(n==0) break;
		memset(g,0,sizeof(g));
		memset(match,0,sizeof(match));
		scanf("%d%d",&m,&k);
		for(int u,v,t,i=1;i<=k;i++)
		{
			scanf("%d%d%d",&t,&u,&v);
				
			if(!u||!v) continue;
			g[u][v]=true;
		}
		int res=0;
		for(int i=1;i<n;i++)
		{
			memset(st,0,sizeof(st));
			if(find(i)) res++;
		}
		printf("%d\n",res);
	}
	return 0;
}

【例题】泥泞的区域

在一块 $N \times M$ 的网格状地面上，有一些格子是泥泞的，其他格子是干净的。

现在需要用一些宽度为 $1$、长度任意的木板把泥地盖住，同时不能盖住干净的地面。

每块木板必须覆盖若干个完整的格子，木板可以重叠。

求最少需要多少木板。

数据范围

$ 1\leq N,M \leq 50 $。

思路

本题中每块泥地 $(i,j)$ 要么被第 $i$ 行的一块横着的木板盖住，要么被第 $j$ 行的一块竖着的木板盖住，二者至少选择一个，这是本题的 $2$ 要素。

于是就可以将所有连续的横着的泥地看成是左部节点，所有连续的竖着的泥地看成是右部节点。对于 $(i,j)$ 这块泥地，直接在所在的横泥地向竖泥地连边。题意也就转化为了二分图的最小覆盖问题。直接求二分图最大匹配即可。

code：

#include<cstdio>
#include<cstring>
using namespace std;
const int N=55;
int match[N*N],h[N*N],nlc,n,m,totx,toty,idx[N][N],idy[N][N];
bool vis[N*N];
struct edge{
	int v,nex;
}e[N*N];
char s[N][N];
void add(int u,int v){e[++nlc].v=v;e[nlc].nex=h[u];h[u]=nlc;}
bool find(int u)
{
	for(int i=h[u];i;i=e[i].nex)
	{
		int v=e[i].v;
		if(vis[v]) continue;
		vis[v]=true;
		if(!match[v]||find(match[v]))
		{
			match[v]=u;
			return true;
		}
	}
	return false;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%s",s[i]+1);
	for(int i=0;i<=n;i++) s[i][0]='.';
	for(int i=0;i<=m;i++) s[0][i]='.';
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
	    {
	    	if(s[i][j]=='*'&&s[i][j-1]=='.') totx++;
	    	idx[i][j]=totx;
		}
	for(int j=1;j<=m;j++)
	    for(int i=1;i<=n;i++)
	    {
	    	if(s[i][j]=='*'&&s[i-1][j]=='.') toty++;
	    	idy[i][j]=toty;
		}
	for(int i=1;i<=n;i++)
	    for(int j=1;j<=m;j++)
	        if(s[i][j]!='.') add(idx[i][j],idy[i][j]);
	int res=0;
	for(int i=1;i<=totx;i++)
	{
		memset(vis,0,sizeof(vis));
		if(find(i)) res++;
	}
	printf("%d\n",res);
	return 0;
}

二分图最大独立集

给定一张无向图 $G =(V,E)$，满足下列条件的点集 $S$ 被称为图的独立集：

1.$S \subseteq V$

２ $\forall x,y \in S,(x,y) \notin E$。

通俗地讲，图的独立集就是“任意两点之间都没有边相连”的点集。包含点数最多的一个就是图的最大独立集。

对应地，“任意两点之间都有一条边相连”的子图被称为无向图的团。点数最多的团被称为图的最大团。

定理

无向图 $G$ 的最大团等于其补图 $G'$ 的最大独立集。

$G'=(V,E')$ 被称为 $G=(V,E)$ 的补图，其中 $E'={(x,y) \notin E}$

~~正确性显然~~。在一些题目中，补图转化思想能成为解答的突破口。

对于一般无向图，最大团、最大独立集是 NPC 问题。

定理

设 $G$ 是有 $n$ 个节点的二分图，$G$ 的最大独立集的大小等于 $n$ 减去最大匹配数。

证明：

选出最多的点构成独立集

$\Leftrightarrow$ 在图中去掉最少的点，使得剩下的点之间没有边。

$\Leftrightarrow$ 用最少点覆盖所有边。

因此，去掉二分图的最小点覆盖，剩余的点就构成二分图的最大独立集。而最小点覆盖等于最大匹配数，故最大独立集大小等于 $n$ 减去最大匹配数。

【例题】骑士放置

给定一个 $N \times M$ 的棋盘，有一些格子禁止放棋子。

问棋盘上最多能放多少个不能互相攻击的骑士（国际象棋的“骑士”，类似于中国象棋的“马”，按照“日”字攻击，但没有中国象棋“别马腿”的规则）。

数据范围

$1 \leq N,M \leq 100$。

思路

~~本题显然是要求一个最大独立集。~~对原棋盘进行黑白染色（按照“马”的行走规则），再把黑色的节点当成左部点，白色的点当成右部点。根据上面的定理，直接求二分图最大匹配即可。

code：

#include<iostream>
#include<algorithm>
#include<cstring>
#define x first
#define y second
#define PII pair<int,int>
using namespace std;
int dx[8]={-2,-2,2,2,-1,-1,1,1};
int dy[8]={-1,1,-1,1,-2,2,-2,2};
const int N=110;
bool st[N][N],g[N][N];
int n,m,k;
PII match[N][N];
bool find(int x,int y)
{
	for(int i=0;i<8;i++)
	{
		int x1=x+dx[i],y1=y+dy[i];
		if(x1<1||x1>n||y1<1||y1>m) continue;
		if(st[x1][y1]||g[x1][y1]) continue;
		st[x1][y1]=true;
		PII t=match[x1][y1];
		if(t.x==0||find(t.x,t.y))
		{
			match[x1][y1]={x,y};
			return true;
		}
	}
	return false;
}
int main()
{
	scanf("%d%d%d",&n,&m,&k);
	for(int a,b,i=1;i<=k;i++)
	{
		scanf("%d%d",&a,&b);
		g[a][b]=true;
	}
	int res=0;
	for(int i=1;i<=n;i++)
	    for(int j=1;j<=m;j++)
	    {
	    	if((i+j)&1||g[i][j]) continue;
	    	memset(st,0,sizeof(st));
	    	if(find(i,j)) res++;
		}
	printf("%d\n",n*m-res-k);//别忘了减去禁止放置的格子
	return 0;
}

以上大部分内容摘自 lyd 大佬的《算法竞赛进阶指南》，仅供个人学习参考用。

posted @ 2021-08-26 16:22 曙诚阅读(254) 评论(0) 收藏举报

刷新页面返回顶部

ListenSnow

看着天边似在眼前 也甘愿赴汤蹈火去走它一遍

二分图学习笔记

二分图的定义

二分图判定

定理

【例题】关押罪犯

数据范围

思路

code:

二分图最大匹配

匈牙利算法（增广路算法）

code:

【例题】棋盘覆盖

数据范围

思路

code：

【例题】車的放置

数据范围

思路

code：

完备匹配

多重匹配

二分图带权匹配

交错树

顶标（顶点标记值）

相等子图

定理

证明：

code：

code：

【例题】Ants

数据范围

思路

code:

二分图最小点覆盖

König 定理

【例题】机器任务

数据范围

思路

code：

【例题】泥泞的区域

数据范围

思路

code：

二分图最大独立集

定理

定理

【例题】骑士放置

数据范围

思路

code：

公告

看着天边似在眼前也甘愿赴汤蹈火去走它一遍