平衡树 Splay 学习笔记
又是被 N 总吊打的一天呢。。。。。
通过学习 Treap,可以发现能够用 Treap 做的平衡树题目其实非常少,这就是因为 Treap 支持的操作太少,基本上用 Treap 就是查找前驱和后继,其他的就做不了了。。。
首先给出 Splay 的模板题。
文艺平衡树
题意
给定一个 \(1\) 到 \(n\) 的序列,多次翻转其中的子序列 \([l,r]\) ,求最终得到的序列。(显然本题就无法用 Treap 做)
Splay
应该是最常用的的平衡树了。
定义
Splay 是一棵平衡二叉树。
核心操作
左旋和右旋,左旋和右旋操作就是在保证中序遍历不变的前提下改变树的高度,但是 Splay 中的旋转和 Treap 的左旋和右旋操作有些不同。
Splay 中旋转时的节点是子节点,不同于 Treap 中的父节点。因此 Splay 中不需要特意注明左旋和右旋,因为若 \(x\) 是 \(y\) 的左儿子,那么旋转过后为了维护中序遍历不变的性质,\(y\) 肯定只能是 \(x\) 的右儿子,可以结合下面的旋转图片理解一下。
但是和 Treap 不同的地方是,Splay 每次操作都会直接把该节点旋转到树根,这是 Splay 的核心。这里举一个很现实的例子来理解这样做的目的。
在视频网站看视频的时候,通常有一小部分的视频是高质量的,当一位用户访问过某一个视频后,那么就代表这个视频可能就是高质量视频。把它旋转到树根就更容易被其他人看到。这其实就是一个缓存的思想。(就当放松一下心情。。。)
但是用严谨的数学思维也可以证明,这样操作后,Splay 的所有操作的均摊复杂度为 \(O(\log n)\)。
Splay 函数
这个函数的功能就是实现将节点旋转到根节点上。
定义 \(Splay(x,k)\) 表示将 \(x\) 点旋转至点 \(k\) 下面。
需要分两大类、四小类(其实就是左右对称,这里以都在根节点的左子树为例)来讨论:
情况一:\(x\) 与它的父亲 \(y\) 以及 \(y\) 的父节点 \(z\) 在同一条链上。
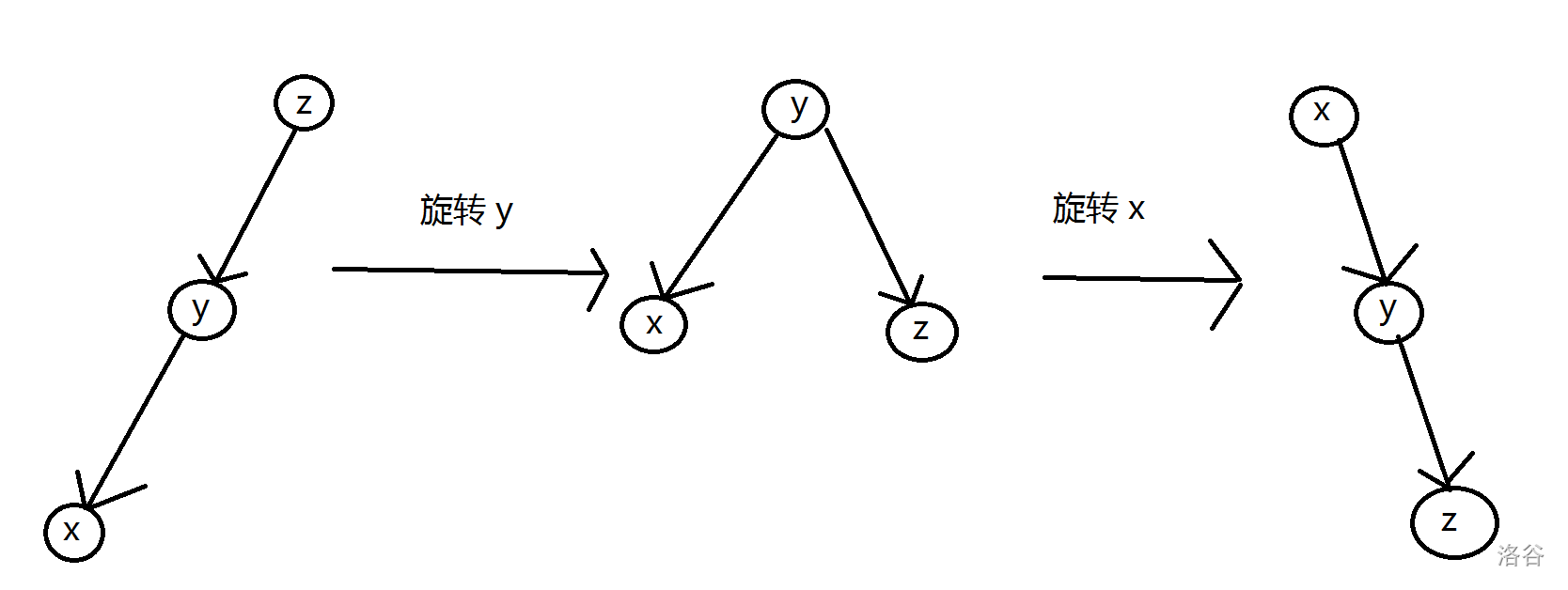
情况二:\(x\) 与它的父亲 \(y\) 以及 \(y\) 的父节点 \(z\) 不在同一条链上。

注意,Splay 的所有旋转都要严格按照上面的顺序旋转,要不然无法保证 \(O(\log n)\) 的均摊时间复杂度。
事实上,\(k\) 的取值通常只有 \(0\) 和 \(root\),要么就是旋转到根节点,要么就是旋转到根节点下面。
插入
对于一般的情况,直接先插入到应该插入的位置,然后旋转到根节点即可。
但是通常会遇到这种情况:把一个序列插入到 \(y\) 的后面,使得中序遍历时,该序列在 \(y\) 的后面。这就体现到 Splay 的优势了,因为这种操作 Treap 就无法实现。
首先找到 \(y\) 的后继 \(z\)。再进行如下操作:
1.将 \(y\) 旋转到根节点。
2.将 \(z\) 旋转到 \(y\) 的下面。
此时 \(z\) 的左子树为比 \(z\) 小的树。同时根据后继的定义,比 \(z\) 小的第一个树就是 \(y\),那么显然 \(z\) 的左子树此时一定为空。接着把要插入的序列先构造成一棵二叉平衡树,再接到 \(z\) 的左子树即可。
删除
在 Splay 中删除 \([l,r]\) 这一段序列。
对于这种情况,Treap 就只能一个个删除。但是 Splay 就不同了。
首先找出 \(l\) 的前驱 \(l-1\) 和 \(r\) 的后继 \(r+1\),再将 \(l-1\) 旋转到根节点,\(r+1\) 旋转到根节点的下面。同样根据前驱和后继的定义,此时 \(r+1\) 的左子树中就是 \([l,r]\)。直接令 \(r+1\) 的左子树为空即可。
其他操作
其他操作就和 Treap 差不多,这里就不过多赘述了。
维护信息
以模板题为例。题目中要求旋转区间 \([l,r]\) ,也就是第 \(l\) 个数到第 \(r\) 个树,那么我们查找的时候就要记录子树的大小 \(size\) 来方便查找第 \(k\) 个数。
同时类似线段树中的区间修改操作,可以用一个懒标记来维护区间翻转的信息,因为如果区间 \([l,r]\) 被翻转了两次,那么就和没有翻转一样。
既然都借鉴了线段树的懒标记,那么干脆也借鉴一下线段树中的 \(pushup\) 和 \(pushdown\) 操作吧。
可以用 \(pushup\) 操作来维护子树的大小(维护信息),用 \(pushdown\) 来下传懒标记。但是这里的 \(pushdown\) 就和线段树中的有些区别了。
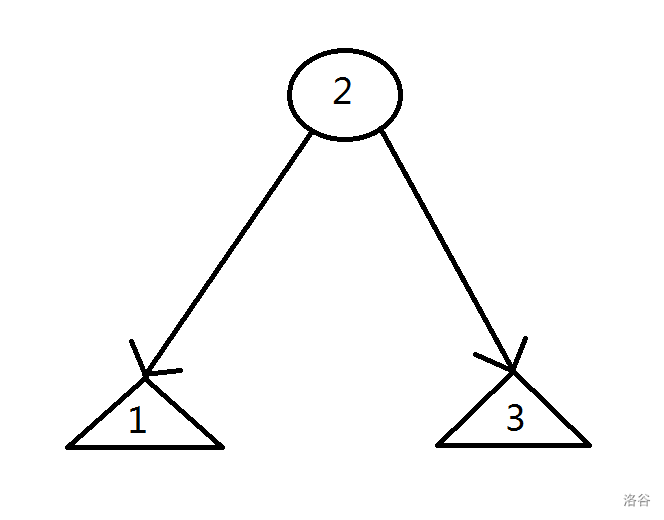
如图中的 \(2\) 号节点(不一定是数字 \(2\))被打上懒标记,那么就说明要翻转 \(1\) 号节点和 \(3\) 号节点,那么就需要先 \(swap(1,3)\)。再把懒标记下传到这两个节点,同时别忘了清空当前函数的信息。如果这两个节点还有儿子,那么递归处理即可。
再借鉴一下线段树中这两个函数的位置。\(pushup\) 就放在旋转函数的最后,\(pushdown\) 放在往下递归之前。
仅限于模板题只要维护这两个信息。在实际应用的时候,通常还要维护更多更复杂的信息。。。。
同时在模板题中,Splay 保证了中序遍历是当前序列的顺序。所以说,实际上 Splay 维护的序列不一定是有序的。(那这样子上面的插入和删除操作岂不就不正确了吗,还是要等到具体问题再来具体分析)
旋转区间
回到本题的问题上来,首先可以找到 \(l\) 的前驱 \(l-1\) 和 \(r\) 的后继 \(r+1\),然后把 \(l-1\) 旋转到根节点上,把 \(r+1\) 旋转到根节点的下面,那么此时 \(r+1\) 节点的左子树中就是区间 \([l,r]\) ,即可打上懒标记。最后直接按照中序遍历输出序列即可。
这里再解释一下为什么 \(r+1\) 节点的左子树就是区间 \([l,r]\)。虽然用过 swap 函数后,Splay 的中序遍历会改变,但是题目要求的是将区间 \([l,r]\) 内的数字翻转,也就是将中序遍历的第 \(l\) 个数字到第 \(r\) 个数字改变,而不是第 \(l\) 大到第 \(r\) 大的数字。而根据中序遍历的性质,当前的节点在中序遍历中的位置就是左子树的大小 \(+1\)。那么只需找到第 \(l-1\) 输出的数和第 \(r+1\) 输出的数,再根据旋转不改变中序遍历的性质。第 \(r+1\) 节点的左子树自然就是区间 \([l,r]\) 中的数了。
模板题 code:
#include<cstdio>
using namespace std;
const int N=1e5+10;
int n,m,root,num;
struct tree{
int son[2],size,tag;
int p,v;//当前节点的父亲,当前节点的值
}tr[N];
template <class T>void swap(T &a,T &b){T t=a;a=b,b=t;} //这样写的好处是可以交换任意类型数据的大小
void push_up(int p){tr[p].size=tr[tr[p].son[0]].size+tr[tr[p].son[1]].size+1;}
void push_down(int p)
{
if(tr[p].tag)
{
swap(tr[p].son[0],tr[p].son[1]);
tr[tr[p].son[0]].tag^=1;
tr[tr[p].son[1]].tag^=1;
tr[p].tag=0;
}
}
void rotate(int x) //旋转操作,注意区分 Treap 中的旋转操作
{
int y=tr[x].p,z=tr[y].p;
int k=tr[y].son[1]==x;//判断x是y的左儿子还是右儿子
tr[z].son[tr[z].son[1]==y]=x,tr[x].p=z;//旋转后x就是祖先节点的儿子
tr[y].son[k]=tr[x].son[k^1],tr[tr[y].son[k]].p=y;//以左旋为例,旋转后x的左儿子变成了y的右儿子,x的左儿子变成了y
tr[x].son[k^1]=y,tr[y].p=x;//别忘了更新该节点的父节点的编号
push_up(y),push_up(x);//先更新子节点,再更新父节点
}
void splay(int x,int k)//splay的核心操作
{
while(tr[x].p!=k) //将y旋转到k下面
{
int y=tr[x].p,z=tr[y].p;
if(z!=k) //如果此时k已经是y的爷爷了,那么就只要旋转一下x即可
{
if((tr[z].son[0]==y)^(tr[y].son[0]==x)) rotate(y);//当异或值为true时,代表x,y,z不在一条链上,
else rotate(x);
}
rotate(x);
}
if(!k) root=x; //如果把x旋转到根节点上,别忘了更新根节点的编号
}
void insert(int v)//因为要满足原序列在splay上的中序遍历有序,插入操作还是类似于Treap
{
int u=root,p=0;//p记录当前节点的父亲
while(u) p=u,u=tr[u].son[v>tr[u].v]; //如果比父节点小,去左子树,反之去右子树
u=++num;
if(p) tr[p].son[v>tr[u].v]=u;//当前插入的不是根节点,那么就要更新父节点的细节
tr[u].size=1;
tr[u].p=p;
tr[u].v=v;
splay(u,0); //别忘了每次操作后都把节点旋转到根节点上
}
int get_k(int k)//这里查找的是中序遍历输出的第k个数
{
int u=root;
bool NLCAKIOI=false;
while(!NLCAKIOI)
{
push_down(u);
if(tr[tr[u].son[0]].size>=k) u=tr[u].son[0];
else if(tr[tr[u].son[0]].size+1==k) return u;
else k-=tr[tr[u].son[0]].size+1,u=tr[u].son[1];//别忘了减去左子树和父节点的大小,原理和 Treap 内查找前驱后继相同
}
return -1;
}
void output(int u)
{
push_down(u);
if(tr[u].son[0]) output(tr[u].son[0]);
if(tr[u].v>=1&&tr[u].v<=n) printf("%d ",tr[u].v);//如果当前节点不是哨兵
if(tr[u].son[1]) output(tr[u].son[1]);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=0;i<=n+1;i++) insert(i);//增加两个哨兵,防止出错
while(m--)
{
int l,r;
scanf("%d%d",&l,&r);
l=get_k(l),r=get_k(r+2);//因为增加了一个哨兵0,所以l-1和r+1在splay的中序遍历位置实际上是l和r+2
splay(l,0),splay(r,l);//把l转到根节点,把r转到根节点的下方
tr[tr[r].son[0]].tag^=1;
}
output(root);
puts("");
return 0;
}
应用 [NOI2004] 郁闷的出纳员
题意
有一家公司,初始员工为 \(0\),现在给定 \(n\) 个操作和一个最低工资标准 \(mink\),如果员工的工资低于 \(mink\) 就会离职。有四种操作类型:
-
\(I\) 命令,格式为 \(I\)_\(k\),表示新建一个工资档案,初始工资为 \(k\)。如果某员工的初始工资低于工资下界,他将立刻离开公司。
-
\(A\) 命令,格式为 \(A\)_\(k\),表示把每位员工的工资加上 \(k\)。
-
\(S\) 命令,格式为 \(S\)_\(k\),表示把每位员工的工资扣除 \(k\)。
-
\(F\) 命令,格式为 \(F\)_\(k\),表示查询第 \(k\) 多的工资。如果 \(k\) 大于员工的总人数,直接输出 \(-1\) 即可。
在最后一行输出离职的总人数,注意因初始工资太低而离开不算在内。
思路
看到有操作类型,那么就肯定是数据结构题。看到要维护动态区间第 \(k\) 大值,那么肯定就是平衡数,而题目中又隐藏着区间删除操作,那么就可以用 Splay 来做本题。
为什么本题的区间第 \(k\) 大值可以用 Splay 来做呢。因为本题中并不包含区间翻转等操作。而根据旋转不改变中序遍历的性质,如果在插入的时候就满足 BST 性质,那么无论旋转多少次,最终得到的中序遍历也是有序的。
但是对于第二种操作类型和第三种操作类型,Splay 虽然支持区间修改操作,但是在这里并不需要。
再仔细观察操作内容。可以看到一定为全局修改操作(瞎 yy 出来的名词,知道意思就好)。那么就可以设一个全局变量 \(delta\) 表示现在的工资与原来的工资的差值。那么会离职的员工就满足 \(k+delta <minv\),也就是 \(k<minv-delta\)。于是就可以查找到第一个 \(\geq minv-delta\) 的节点 \(r\),那么要删除的区间就是 \([l+1,r-1]\)。因为在最初的时候要加入两个哨兵防止出错。
接下来根据最上面提到的区间修改操作的方法,把 \(r\) 旋转到根节点,再把 \(l\) 旋转到根节点的左儿子(因为在插入时满足了 BST 性质,旋转后也会满足)。那么要删除的区间就是 \(l\) 的右儿子了,直接令 \(tr[l].son[1]=0\) 即可。但是别忘了更新一下 \(size\)。求第 \(k\) 大数时会用到。
code:
#include<cstdio>
using namespace std;
const int N=1e5+10;
const int INF=0x3f3f3f3f;
struct tree{
int son[2],p,v,size;
}tr[N];
int n,minv,delta,tot,num,root;
void push_up(int p){tr[p].size=tr[tr[p].son[0]].size+tr[tr[p].son[1]].size+1;}
void rotate(int x)
{
int y=tr[x].p,z=tr[y].p;
int k=tr[y].son[1]==x;
tr[z].son[tr[z].son[1]==y]=x,tr[x].p=z;
tr[y].son[k]=tr[x].son[k^1],tr[tr[y].son[k]].p=y;
tr[x].son[k^1]=y,tr[y].p=x;
push_up(y),push_up(x);
}
void splay(int x,int k)
{
while(tr[x].p!=k)
{
int y=tr[x].p,z=tr[y].p;
if(z!=k)
{
if((tr[z].son[1]==y)^(tr[y].son[1]==x)) rotate(x);
else rotate(y);
}
rotate(x);
}
if(!k) root=x;
}
int insert(int v)
{
int u=root,p=0;
while(u) p=u,u=tr[u].son[v>tr[u].v];
u=++num;
if(p) tr[p].son[v>tr[p].v]=u;
tr[u].size=1;
tr[u].p=p;
tr[u].v=v;
splay(u,0);
return u;
}
int get(int v)//第一个大于等于
{
int u=root,res;
while(u)
{
if(tr[u].v>=v) res=u,u=tr[u].son[0];//有点类似于二分查找,后面找到的一定更优,在Treap查找前驱时证明过
else u=tr[u].son[1];
}
return res;
}
int get_k(int k)//第k小数
{
int u=root;
while(u)
{
if(tr[tr[u].son[0]].size>=k) u=tr[u].son[0];
else if(tr[tr[u].son[0]].size+1==k) return tr[u].v;
else k-=tr[tr[u].son[0]].size+1,u=tr[u].son[1];
}
return -1;
}
int main()
{
scanf("%d%d",&n,&minv);
int L=insert(-INF),R=insert(INF);
while(n--)
{
char op[2];
int k;
scanf("%s%d",op,&k);
if(op[0]=='I')
{
if(k>=minv) k-=delta,insert(k),tot++;//因为Splay中存的工资要加上上delta才是真实的工资。所以要先减去一个delta
}
else if(op[0]=='A') delta+=k;
else if(op[0]=='S')
{
delta-=k;
R=get(minv-delta);
splay(R,0),splay(L,R);
tr[L].son[1]=0;
push_up(L),push_up(R);
}
else
{
if(k>tr[root].size-2) puts("-1");
else printf("%d\n",get_k(tr[root].size-k)+delta);//因为get_k求的是第 k小数,而我们要求的是第k+1大数(有一个哨兵),也就是第(tr[root].size-(k+1)+1)小数,同时别忘了加上改动的工资
}
}
printf("%d\n",tot-(tr[root].size-2));//别忘了减去哨兵
return 0;
}
应用 [HNOI2012]永无乡
题意
给定 \(n\) 个岛屿,每座岛都有一个独一无二的重要度。给定 \(m\) 座桥,接下来有 \(q\) 个操作,有两种操作类型:
1.在岛屿 \(a\) 所有能到达的岛屿中,查找重要度第 \(k\) 小的岛屿的编号。
2.在岛屿 \(a\) 和岛屿 \(b\) 中添加一座桥。
思路
首先转化一下题目要求的操作类型。查询动态第 \(k\) 小值,合并两个联通块。
对于查询第 \(k\) 小值,只要在插入 Splay 时维护中序遍历有序即可,和上面一道题类似。
而对于合并操作,不同于最上面提到的区间添加,这里的合并同时还要保证合并后中序遍历仍然有序,就不能直接当成区间添加来做。也就只能一个一个节点依次合并。显然这样的复杂度太高了,于是需要用到一种合并优化:
启发式合并
在并查集按秩合并时,如果把秩定义为并查集的大小,那么其实也就是启发式合并。同理,可以把节点个数少的 Splay 合并到节点个数多的 Splay 上。这样其实也就保证了合并时添加的节点个数最少。将 \(n\) 个孤立点合并到一起的时间复杂度也就从 \(O(n^2)\) 降低到了 \(O(n \log n)\)。同时在插入时将节点旋转到根节点还要 \(O(\log n)\),故 Splay 启发式合并的复杂度就为 \(O(n \log^2 n)\)。
其他的操作就和上一道题类似了,只是需要注意一下区分 \(root[b]\) 和 \(b\),\(b\) 是一个联通块岛屿的代表节点,也就是并查集中的根节点,而 \(root[b]\) 是在这棵 Splay 中的根节点。
code:
#include<cstdio>
using namespace std;
const int N=2e6+10;
int num,n,m,q,root[N],fa[N];
struct node{
int son[2],p,v,id,size;
}tr[N];
int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
void push_up(int p){tr[p].size=tr[tr[p].son[0]].size+tr[tr[p].son[1]].size+1;}
void rotate(int x)
{
int y=tr[x].p,z=tr[y].p;
int k=tr[y].son[1]==x;
tr[z].son[tr[z].son[1]==y]=x,tr[x].p=z;
tr[y].son[k]=tr[x].son[k^1],tr[tr[y].son[k]].p=y;
tr[x].son[k^1]=y,tr[y].p=x;
push_up(y),push_up(x);
}
void splay(int x,int k,int b)
{
while(tr[x].p!=k)
{
int y=tr[x].p,z=tr[y].p;
if(z!=k)
{
if((tr[z].son[1]==y)^(tr[y].son[1]==x)) rotate(x);
else rotate(y);
}
rotate(x);
}
if(!k) root[b]=x;
}
void insert(int v,int id,int b)
{
int u=root[b],p=0;
while(u) p=u,u=tr[u].son[v>tr[u].v];
u=++num;
if(p) tr[p].son[v>tr[p].v]=u;
tr[u].size=1,tr[u].id=id,tr[u].v=v,tr[u].p=p;
splay(u,0,b);
}
void dfs(int u,int b)
{
if(tr[u].son[0]) dfs(tr[u].son[0],b);
if(tr[u].son[1]) dfs(tr[u].son[1],b);
insert(tr[u].v,tr[u].id,b);
}
int get_k(int k,int b)
{
int u=root[b];
while(u)
{
if(tr[tr[u].son[0]].size>=k) u=tr[u].son[0];
else if(tr[tr[u].son[0]].size+1==k) return tr[u].id;
else k-=tr[tr[u].son[0]].size+1,u=tr[u].son[1];
}
return -1;
}
int main()
{
scanf("%d%d",&n,&m);
for(int v,i=1;i<=n;i++)
{
scanf("%d",&v);
root[i]=fa[i]=i;
tr[i].id=i,tr[i].v=v,tr[i].size=1;
}
num=n;
while(m--)
{
int a,b;
scanf("%d%d",&a,&b);
a=find(a),b=find(b);
if(a!=b)
{
if(tr[root[a]].size>tr[root[b]].size) fa[b]=a,dfs(root[b],a);//启发式合并
else fa[a]=b,dfs(root[a],b);
}
}
scanf("%d",&q);
while(q--)
{
char op[2];
int x,y,k;
scanf("%s",op);
if(op[0]=='Q')
{
scanf("%d%d",&x,&k);
x=find(x);
if(k>tr[root[x]].size) puts("-1");
else printf("%d\n",get_k(k,x));
}
else
{
scanf("%d%d",&x,&y);
int a=find(x),b=find(y);
if(a!=b)
{
if(tr[root[a]].size>tr[root[b]].size) fa[b]=a,dfs(root[b],a);
else fa[a]=b,dfs(root[a],b);
}
}
}
return 0;
}
综合应用 [NOI2005] 维护数列
谨以此题纪念那些我们调了一个下午的题目。。。。
题意
维护一个序列,满足六种操作:
1.插入一段序列。
2.删除一段序列。
3.将一段序列全部赋值为 \(c\)。
4.翻转序列 \([l,r]\)。
5.求一段序列的和。
6.求一段序列中的最大子序列和。
思路
应该是 Splay 能够支持的所有操作了。。。考验代码能力以及耐心。
Splay 需要维护的信息很多。
\(rev\) 记录区间是否翻转,\(same\) 记录是否赋值成相同的数(先把该节点的 \(val\) 赋值成该值)。这两个信息就是懒标记。
用 \(maxv\) 表示最大子段和,用 \(ls\) 表示最大前缀和,用 \(rs\) 表示最大后缀和(可以参考小白逛公园)。
用 \(sum\) 来维护区间和。
以及一些常规的信息。
同时需要注意,每个节点维护的值是发生懒标记之前的,还是发生之后的(自己定义的),如果搞反了就会发生错误。为了方便表达以及正确性,这里记录的是发生懒标记之后的值。所以在下推懒标记的时候也要更新左右儿子的信息。其实也和复杂线段树类似。
本题并未要求求动态区间第 \(k\) 大值,同时需要满足中序遍历是原序列。那么就不能和前面的题一样的建树方式了,而是要以序列的中间为根节点,再向左右两边递归建树。也正因如此,插入序列和删除序列的操作就很简单了。和最上面提到的方法一样。
注意,本题中的序列虽然满足时时刻刻不超过 \(500000\),但是在其中删除和添加的节点就很多了。这里就要提到 Splay 的一种机制:
内存回收机制
在删除一段序列操作时,删除的子树可能会非常大,就可以想办法把这些节点存下来留在以后用。也就是可以再开一个盏,记录每一个节点有没有在被使用。删除了节点就代表这些节点还可以在使用。要插入新节点的时候直接在这个数组中找到没有在用的节点即可。(有点类似于到垃圾站回收物品)这样做就可以大大减少空间消耗。
code:
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int N=5e5+10;
const int INF=0x3f3f3f3f;
struct tree{
int son[2],p,v,size;
bool same,rev;
int rv,lv,maxv,sum;
}tr[N];
int rec[N],top,w[N],n,m,root;
void push_up(int p)
{
tree &u=tr[p],&l=tr[u.son[0]],&r=tr[u.son[1]]; //引用地址,方便写,也方便调试
u.size=l.size+r.size+1;
u.sum=l.sum+r.sum+u.v;//注意和线段树的区别,当前节点的值还要加上
u.lv=max(l.lv,l.sum+u.v+r.lv);//左子树的最大前缀和,左子树的和+当前节点+右子树的最大前缀和
u.rv=max(r.rv,r.sum+u.v+l.rv);//同上
u.maxv=max(max(l.maxv,r.maxv),l.rv+u.v+r.lv);//左右子树的最大子序列和,左子树的后缀+当前节点+右子树的前缀
}
void push_down(int p)
{
tree &u=tr[p],&l=tr[u.son[0]],&r=tr[u.son[1]];
if(u.same)
{
u.same=u.rev=false;
if(u.son[0]) l.same=1,l.v=u.v,l.sum=l.size*l.v;//别把哨兵更新了
if(u.son[1]) r.same=1,r.v=u.v,r.sum=r.size*r.v;//同时需要注意,不能same^=1,因为修改两次不等于没修改
if(u.v>0)
{
if(u.son[0]) l.lv=l.rv=l.maxv=l.sum;
if(u.son[1]) r.lv=r.rv=r.maxv=r.sum;
}
else
{
if(u.son[0]) l.lv=l.rv=0,l.maxv=u.v;
if(u.son[1]) r.lv=r.rv=0,r.maxv=u.v;
}
}
else if(u.rev)
{
u.rev=0,l.rev^=1,r.rev^=1;
swap(l.lv,l.rv),swap(r.lv,r.rv);//需要注意rev是对左右儿子而言,此时的左右儿子已经翻转过了,现在要做的是翻转左右儿子的左右儿子
swap(l.son[0],l.son[1]),swap(r.son[0],r.son[1]);//也就是当 p.rev=1 时,因为要储存的是下推懒标记后的信息,所以p的左右儿子已经翻转过了
}
}
void rotate(int x)
{
int y=tr[x].p,z=tr[y].p;
int k=tr[y].son[1]==x;
tr[z].son[tr[z].son[1]==y]=x,tr[x].p=z;
tr[y].son[k]=tr[x].son[k^1],tr[tr[y].son[k]].p=y;
tr[x].son[k^1]=y,tr[y].p=x;
push_up(y),push_up(x);
}
void splay(int x,int k)
{
while(tr[x].p!=k)
{
int y=tr[x].p,z=tr[y].p;
if(z!=k)
{
if((tr[z].son[1]==y)^(tr[y].son[1]==x)) rotate(x);
else rotate(y);
}
rotate(x);
}
if(!k) root=x;
}
int build_tree(int l,int r,int p)//当前左右端点,父节点
{
int mid=l+r>>1;
int u=rec[top--];
tr[u].p=p,tr[u].v=tr[u].maxv=tr[u].sum=w[mid],tr[u].size=1;
tr[u].son[0]=tr[u].son[1]=0;//如果不加这两行初始化0就过不了
tr[u].same=tr[u].rev=0;
if(w[mid]>0) tr[u].lv=tr[u].rv=w[mid];//前缀和以及后缀和可以为空
if(l<mid) tr[u].son[0]=build_tree(l,mid-1,u);//-1,与线段树区分
if(r>mid) tr[u].son[1]=build_tree(mid+1,r,u);
push_up(u);
return u;
}
void dfs(int u)//回收节点
{
if(tr[u].son[0]) dfs(tr[u].son[0]);
if(tr[u].son[1]) dfs(tr[u].son[1]);
rec[++top]=u;
}
int get_k(int k)
{
int u=root;
while(u)
{
push_down(u);//别忘了下推懒标记
if(tr[tr[u].son[0]].size>=k) u=tr[u].son[0];
else if(tr[tr[u].son[0]].size+1==k) return u;
else k-=tr[tr[u].son[0]].size+1,u=tr[u].son[1];
}
}
int main()
{
for(int i=1;i<N;i++) rec[++top]=i;
scanf("%d%d",&n,&m);
tr[0].maxv=w[0]=w[n+1]=-INF;//哨兵,防止出错
for(int i=1;i<=n;i++) scanf("%d",&w[i]);
root=build_tree(0,n+1,0);
// dfs(root);
while(m--)
{
char s[12];
int posi,tot,k;
scanf("%s",s);
if(!strcmp(s,"INSERT"))//插入
{
scanf("%d%d",&posi,&tot);//[posi+1,posi+tot]
for(int i=1;i<=tot;i++) scanf("%d",&w[i]);
int l=get_k(posi+1),r=get_k(posi+2); //在posi和posi+1之间插入,注意哨兵的存在
splay(l,0),splay(r,l);
int u=build_tree(1,tot,r);
tr[r].son[0]=u;//别忘了让r的左儿子指向该序列
push_up(r),push_up(l);
}
else if(!strcmp(s,"DELETE"))//删除
{
scanf("%d%d",&posi,&tot);//删除的区间是[posi,posi+tot-1]
int l=get_k(posi),r=get_k(posi+tot+1);//posi,posi+tot
splay(l,0),splay(r,l);
dfs(tr[r].son[0]);//回收节点
tr[r].son[0]=0;
push_up(r),push_up(l);
}
else if(!strcmp(s,"MAKE-SAME"))//修改一致
{
scanf("%d%d%d",&posi,&tot,&k);//[posi,posi+tot-1]
int l=get_k(posi),r=get_k(posi+tot+1);
splay(l,0),splay(r,l);
tree &s=tr[tr[r].son[0]];//这段序列所在子树的根节点
s.same=1,s.v=k,s.sum=s.size*k;
if(k>0) s.lv=s.rv=s.maxv=s.sum;
else s.lv=s.rv=0,s.maxv=k;
push_up(r),push_up(l);
}
else if(!strcmp(s,"REVERSE"))//翻转
{
scanf("%d%d",&posi,&tot);
int l=get_k(posi),r=get_k(posi+tot+1);
splay(l,0),splay(r,l);
tree &s=tr[tr[r].son[0]];
s.rev^=1;
swap(s.lv,s.rv);
swap(s.son[0],s.son[1]);
push_up(r),push_up(l);
}
else if(!strcmp(s,"GET-SUM"))//求和
{
scanf("%d%d",&posi,&tot);
int l=get_k(posi),r=get_k(posi+tot+1);
splay(l,0),splay(r,l);
printf("%d\n",tr[tr[r].son[0]].sum);
}
else printf("%d\n",tr[root].maxv);//最大子序列和,因为是对整个序列,直接输出根节点的最大子序列和即可
}
return 0;
}
动态开点 [SCOI2014]方伯伯的OJ
维护一个 \(1 \sim n\) 的序列,初始时,各个位置的排名和编号就是其下标,需要支持四种操作:
1.将编号为 \(x\) 的点的编号改为 \(y\)。
2.将编号为 \(x\) 的用户的排名提升到 \(rank\) \(1\)。
3.将编号为 \(x\) 的用户的排名降低到 \(rank\) \(n\)。
4.查询排名为 \(x\) 的用户的编号。
强制在线。
数据范围
\(1 \leq n \leq 10^8,1\leq m \leq 10^5\)。
思路
如果不看数据范围,本题就是一道平衡树的板子题。 但是 \(n \leq 10^8\) 注定了本题的不平凡。
注意到操作次数只有 \(m \leq 10^5\) 次,也就是实际用到的用户的编号很少。于是就可以考虑动态开点splay。(参考了froggy大佬的博客)
具体来说,就是把一段连续的没有用到的区间上的节点合并到一个节点上,需要用到其中的节点时再把这个节点分裂出来(所有点都属于且仅属于一个区间,具体的分裂操作可以看代码)。
而对于将一个节点的排名修改到第一位或最后一位的操作。联系到 \(rank_u=tr[tr[u].son[0]].size+1\) (此处的 \(u\) 表示 \(u\) 节点所表示的区间的最左侧的点),以将 \(u\) 修改到第一位为例,先将 \(u\) 转到根节点上,再把 \(u\) 的左子树全部接到 \(u\) 的右子树中排名最小的节点的左子树中即可。
当然,因为用到了动态开点,那么 \(u\) 所在节点的编号就不一定为 \(u\) 了。事实上,可以将所有区间的右端点的编号记录到 map 中,查询 \(u\) 所在的节点的编号,也就是查询第一个右端点大于等于 \(u\) 的节点的编号。
code:
#include<cstdio>
#include<ctime>
#include<cstdlib>
#include<iostream>
#include<map>
using namespace std;
const int N=2e5+10;
map<int,int> M;
const bool NLCAKIOI=true;
int tot,n,m,root,a;
struct tree{
int son[2],l,r,siz,fa;
}tr[N];
void read(int& x)
{
x=0;int f=1;char c;while(!isdigit(c=getchar())) f=c^'-'?1:-1;
while(x=x*10+(c&15),isdigit(c=getchar()));x*=f;
}
int newnode(int l,int r)//新开一个叶子节点
{
tot++;
tr[tot].l=l;tr[tot].r=r;
tr[tot].son[0]=0;tr[tot].son[1]=0;
tr[tot].siz=tr[tot].r-tr[tot].l+1;
return tot;
}
void push_up(int p){tr[p].siz=tr[tr[p].son[0]].siz+tr[tr[p].son[1]].siz+tr[p].r-tr[p].l+1;}
void rotate(int x)
{
int y=tr[x].fa,z=tr[y].fa,k=tr[y].son[1]==x;
tr[z].son[y==tr[z].son[1]]=x;tr[x].fa=z;
tr[y].son[k]=tr[x].son[k^1],tr[tr[x].son[k^1]].fa=y;
tr[x].son[k^1]=y,tr[y].fa=x;
push_up(y),push_up(x);
}
void splay(int x,int k)
{
while(tr[x].fa!=k)
{
int y=tr[x].fa,z=tr[y].fa;
if(z!=k)
{
if((tr[y].son[1]==x)^(tr[z].son[1]==y)) rotate(x);
rotate(y);
}
rotate(x);
}
if(!k) root=x;
}
int get_k(int x)//查找排名为x的用户
{
int u=root;
while(NLCAKIOI)
{
if(tr[tr[u].son[0]].siz>=x) u=tr[u].son[0];
else if(tr[tr[u].son[0]].siz+tr[u].r-tr[u].l+1<x) x-=tr[tr[u].son[0]].siz+tr[u].r-tr[u].l+1,u=tr[u].son[1];
else return tr[u].l+x-tr[tr[u].son[0]].siz-1;
}
}
int rank(int k)//查找用户k的排名
{
splay(k,0);
return tr[tr[k].son[0]].siz+1;
}
void split(int k,int x)//分裂
{
int l=0,r=0;
if(tr[k].l==tr[k].r) return ;//如果已经被分裂出来就没必要继续分裂了
M[x]=k;
if(tr[k].l!=x) //左半边单独形成一个区间
{
l=M[x-1]=newnode(tr[k].l,x-1);
tr[l].fa=k;
tr[l].son[0]=tr[k].son[0];
tr[tr[l].son[0]].fa=l;
tr[k].son[0]=l;
}
if(tr[k].r!=x) //右半边单独形成一个区间
{
r=M[tr[k].r]=newnode(x+1,tr[k].r);
tr[r].fa=k;
tr[r].son[1]=tr[k].son[1];
tr[tr[r].son[1]].fa=r;
tr[k].son[1]=r;
}
tr[k].l=tr[k].r=x; //本身单独形成一个区间
if(l) push_up(l);
if(r) push_up(r);
push_up(k);
}
void change(int u,int k)
{
splay(u,0);
if(!tr[u].son[k]) return ;//如果本身已经是第一(倒数第一)名
if(!tr[u].son[k^1]) //如果本身是倒数第一(第一),要修改成第一(倒数第一)
{
tr[u].son[k^1]=tr[u].son[k];
tr[u].son[k]=0;
}
else
{
u=tr[u].son[k^1];
while(tr[u].son[k]) u=tr[u].son[k];//右(左)子树中排名最小(大)的节点
tr[tr[root].son[k]].fa=u;//将另一半子树直接接到u下面
tr[u].son[k]=tr[root].son[k];
tr[root].son[k]=0;
splay(tr[u].son[k],0);//保证O(logn)的深度
}
}
int main()
{
read(n),read(m);
root=M[n]=newnode(1,n);//初始时所有的节点都没有用过
for(int opt,x,y,i=1;i<=m;i++)
{
read(opt),read(x);x-=a;
if(opt==1)
{
read(y);y-=a;
int pos=(*M.lower_bound(x)).second;
split(pos,x);a=rank(pos);
tr[pos].l=tr[pos].r=y;
M[y]=pos;
}
else if(opt==2||opt==3)
{
int pos=(*M.lower_bound(x)).second;
split(pos,x);
a=rank(pos);
change(pos,opt-2);
}
else a=get_k(x);
printf("%d\n",a);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号