数位 DP 学习笔记

数位统计 DP 是与数字相关的一类计数问题。在这类题目中，一般给定一些限制条件，求满足限制条件的第 $K$ 小的数是多少，或者求在区间 $[L,R]$ 内有多少个满足限制条件的数。

计数问题

给定两个正整数 $a$ 和 $b$，求在 $[a,b]$ 中的所有整数中，$0 \sim 9$ 中每个数各出现了多少次。

数据范围

对于 $30\%$ 的数据，保证 $a\le b\le10^6$；

对于 $100\%$ 的数据，保证 $1\le a\le b\le 10^{12}$。

思路

设 $f[x,k]$ 表示 $k$ 在 $1 \sim x$ 中出现的次数，那么原问题就可以转化为求 $f[b,k]-f[a-1,k](0\leq k \leq9)$。

考虑当 $x=\overline{abcdefg}$ 时。假设现在要让第 $4$ 位为 $k$。那么就可以分两种情况来讨论。

1.前面三位填的数小于 $abc$，那么此时第 $4$ 位填 $k$。后面的位数怎么填都可以满足题意，那么对答案的贡献就是 $abc*10^3$。

2.前面三位填的数等于 $abc$，那么此时如果 $k =d$，那么后面三位填的数就必须小于等于 $efg$ ，对答案的贡献就是 $efg+1$（还有一个 $000$）；如果此时 $k < d$，那么后面怎么填都可以，对答案的贡献就是 $10^3$；如果 $k>d$，则对答案没有贡献。

其他位置同理。当然填第一位时不考虑第一种情况。

当然，$0$ 需要特殊考虑一下，$0$ 只能从第二位开始填起，同时在情况二时，前面填的数不能为 $0$，因为本题中不考虑前导零。

code：

#include<cstdio>
#include<vector>
using namespace std;
#define int long long
int power(int a,int b){int res=1;while(b--) res*=a;return res;}
int get(vector<int> nums,int l,int r){int res=0;for(int i=l;i>=r;i--) res=res*10+nums[i];return res;}
int count(int n,int x)
{
	vector<int> nums;
	while(n)
	{
	    nums.push_back(n%10);
	    n/=10;
	}
	n=nums.size();
	int res=0;
	for(int i=x!=0?n-1:n-2;i>=0;i--)
	{
		if(i<n-1)
		{
			res+=get(nums,n-1,i+1)*power(10,i);
			if(x==0) res-=power(10,i);
		}
		if(nums[i]==x) res+=get(nums,i-1,0)+1;
		if(nums[i]>x) res+=power(10,i);
	}
	return res;
}
signed main()
{
	int a,b;
	scanf("%lld%lld",&a,&b);
	for(int i=0;i<10;i++) printf("%lld ",count(b,i)-count(a-1,i));
	puts("");
	return 0;
}

度的数量

求给定区间 $[X,Y]$ 中满足下列条件的整数个数：这个数恰好等于 $K$ 个互不相等的 $B$ 的整数次幂之和。

例如，设 $X=15,Y=20,K=2,B=2$，则有且仅有下列三个数满足题意：

$17=2^4+2^0$

$18=2^4+2^1$

$20=2^4+2^2$

数据范围

$1 \leq X \leq Y \leq 2^{31}-1$

$1 \leq K \leq 20$

$2 \leq B \leq 10$

思路

分析一下题面，可以发现一个数 $x$ 满足题意，当且仅当 $x \in [X,Y]$，并且 $x$ 的 $B$ 进制表示是一个 $1$ 的个数为 $K$ 的 $01$ 序列。

和上一题类似，先求出 $[1,Y]$ 中满足题意的数的个数，再求出 $[1,X]$ 中满足题意的数的个数。（数位 DP 常用技巧，利用前缀和的思想，将求区间内的数转化为两个区间内数相减）

设 $f[N]$ 表示 $1 \sim N$ 中满足题意的数的个数。。

设 $N$ 在 $B$ 进制表示下的第 $i$ 位为 $a$，前面的数已经填了 $tot$ 个 $1$，当：

$a=0$，那么构造的数中这一位只能为 $0$，后面也不能随便填，因为可能最终构造的数会大于 $N$。所以要交给下一位处理；

$a=1$，如果构造的数这一位填 $0$ 时，后面怎么填剩下的 $k-tot$ 个 $1$，最终的数都不会大于 $N$；对答案的贡献也就是 $C_{i-1}^{k-tot}$；如果构造的数这一位填 $1$。那么就和第一种情况类似，交给下一位处理，同时也要 $tot++$。

$a>1$，这一位填 $0$ 和第二种情况一样，但是这一位填 $1$ 时，后面怎么填还是在 $[1,N]$ 中。对答案的贡献就是 $C_{x-1}^{k-tot-1}$。此时后面的位数也就没必要枚举了。因为枚举下一位的原因是无法保证后面怎么填都在范围内。此时已经保证了，就不需要枚举了。

$a>1$
通过上面这种关系可以发现，所有的情况构成一棵树，如下图所示。

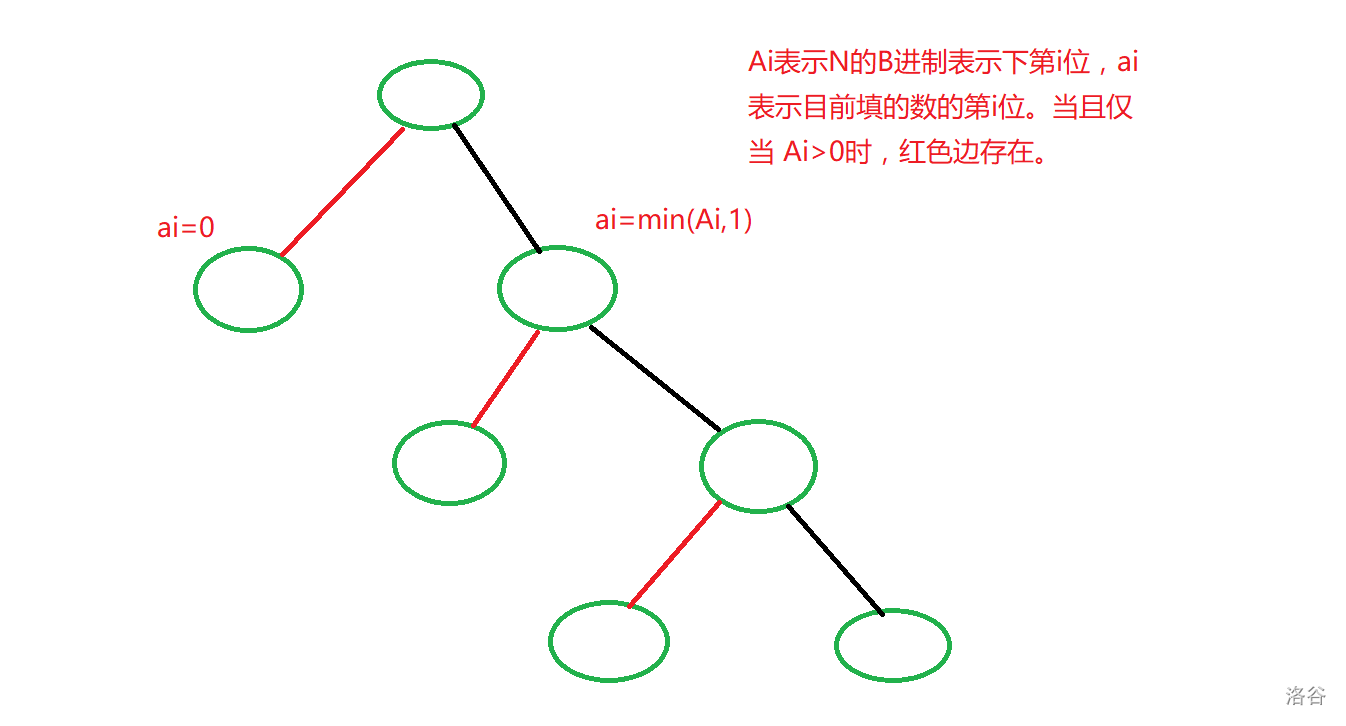
最终的答案就是所有叶子节点的方案相加。

code：

#include<cstdio>
#include<vector>
using namespace std;
const int N=35;//二进制最多有32位 
int x,y,k,b,f[N][N];
void init()
{
	for(int i=0;i<N;i++)
	    for(int j=0;j<=i;j++)
	        if(!j) f[i][j]=1;else f[i][j]=f[i-1][j-1]+f[i-1][j];
}
int query(int n)
{
	int res=0,tot=0;
	vector<int> nums;
	nums.clear();
	while(n){nums.push_back(n%b),n/=b;}
	for(int i=nums.size()-1;i>=0;i--)
	{
		if(nums[i])
		{
			res+=f[i][k-tot];
			if(nums[i]>1)
			{
				res+=f[i][k-tot-1];
				break;
			}
			tot++;
			if(tot>k) break;
		}
		if(!i&&tot==k) res++;//考虑深度最深的右叶子节点
	}
	return res;
}
int main()
{
	init();
	scanf("%d%d%d%d",&x,&y,&k,&b);
	printf("%d\n",query(y)-query(x-1));
	return 0;
}

数字游戏

定义一个数字为不下降数，当且仅当这个数从左到右各位数字呈非下降关系，如 $123$，$446$。

给定一个整数闭区间 $[a,b]$，求这个区间内有多少个不降数。

数据范围

$1 \leq a \leq b \leq 2^{31}-1$

思路

还是将问题转化为区间差。

设 $h[N]$ 表示 $1 \sim N$ 中的不下降数的个数。分类讨论，画出树状关系图。

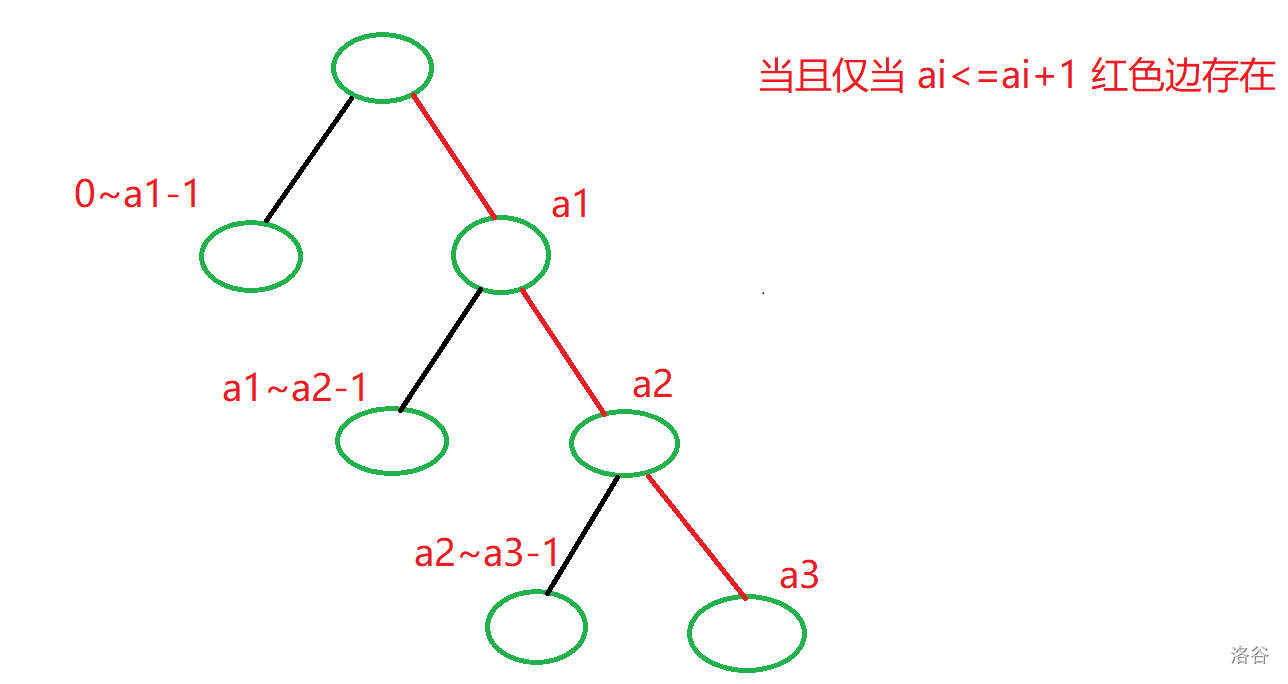
显然，当第 $i$ 位填的数小于 $a_i$ 时，后面的数只要满足非严格单调递增即可。考虑预处理出这些方案数

设 $f[i][j]$ 表示数位为 $i$，且最高位为 $j$ 的不下降数的个数。易得状态转移方程：

$f[i][j]=\sum_{k=j}^{9}f[i-1][k]$。

最后，别忘了特判 $N$ 本身是否是一个非下降数。

code：

#include<cstdio>
#include<vector>
using namespace std;
const int N=15;
int a,b,f[N][N];
void init()
{
	for(int i=0;i<=9;i++) f[1][i]=1;
	for(int i=2;i<=10;i++)
	    for(int j=0;j<=9;j++)//可以优化，但没必要 
		    for(int k=j;k<=9;k++)
			    f[i][j]+=f[i-1][k];  
}
int query(int n)
{
	if(!n) return 1;//注意特判0 
	vector<int>nums;
	nums.clear();
	while(n) nums.push_back(n%10),n/=10;
	int res=0; 
	nums.push_back(0);
	for(int i=nums.size()-2;i>=0;i--)
	{
	    
		for(int j=nums[i+1];j<nums[i];j++) res+=f[i+1][j];
		if(i&&nums[i]>nums[i-1]) break; 
		if(!i) res++;//特判自身 
	}
	return res;
}
int main()
{
	init();
	while(scanf("%d%d",&a,&b)!=EOF) printf("%d\n",query(b)-query(a-1));
	return 0;
}

[SCOI2009] windy 数

不含前导零且相邻两个数字之差至少为 $2$ 的正整数被称为 windy 数。求 $[a,b]$ 中 windy 数的数量。

数据范围

$1 \leq a \leq b \leq 2 \times 10^9$。

思路

和上一道题类似。需要预处理出一个数组。

设 $f[i][j]$ 表示一共有 $i$ 位，最高位为 $j$ 的 windy 数的个数。得到转移方程：

$f[i][j]=\sum_{0}^{j-2}f[i-1][k]+\sum_{j+2}^{9}f[i-1][k]$。

但是需要注意，上一道题填 $\overline{0000}$ 前导零对后面的数是没有影响，但是本题就不一样了，因为如果和上一题枚举方式相同，那么形如 $\overline{03574}$ 这样的数字就不会被计算为 windy 数，所以需要特判一下位数小于 $N$ 的数，由于最高位填的是 $0$，后面怎么填都不会超过 $N$。直接统计 $\sum_{i=1}^{|n|-1}\sum_{j=1}^{9}f[i][j]$ 即可。

code：

#include<cstdio>
#include<vector>
using namespace std;
const int N=15;
int f[N][N],a,b;
int abs(int a){return a>0?a:-a;}
void init()
{
	for(int i=0;i<=9;i++) f[1][i]=1;//用到f[1][0] 时前面肯定不会是0
	for(int i=2;i<=10;i++)
	    for(int j=0;j<=9;j++)
		    for(int k=0;k<=9;k++)
			    if(abs(j-k)>=2) f[i][j]+=f[i-1][k]; 
}
int query(int n)
{
	int res=0;
	vector<int>nums;
	nums.clear();
	while(n) nums.push_back(n%10),n/=10;
	nums.push_back(-1);//因为最高位不能是0
	for(int i=nums.size()-2;i>=0;i--)
	{
		for(int j=0;j<nums[i];j++)
		    if(abs(j-nums[i+1])>=2) res+=f[i+1][j];
		if(abs(nums[i]-nums[i+1])<2) break;
		if(!i) res++;
	} 
	for(int i=1;i<nums.size()-1;i++)
	    for(int j=1;j<=9;j++) res+=f[i][j];
	return res;
}
int main()
{
	init();
	scanf("%d%d",&a,&b);
	printf("%d\n",query(b)-query(a-1));
	return 0;
}

数字游戏 II

定义一个数为取模数，当且仅当这个数字各位上之和 $\bmod N=0$。

给定 $a,b$,求在 $[a,b]$ 内的取模数个数。

数据范围

$1 \leq a,b \leq 2^{31}-1$,

$1 \leq N <100$

思路

设 $f[i][j][k]$ 表示一共有 $i$ 位，最高位为 $j$，各位上的数字之和模 $N$ 为 $k$ 的数字的个数。得到状态转移方程：

$f[i][j][k]=\sum_{t=0}^{9}f[i-1][t][(k-j)\% P]$。

假设前面位填的数字之和是 $sum$，当前位填的是 $x$，后面几位需要填的数字之和为 $res$。

就有 $(sum+x+res) \bmod N=0$，移项得 $(res+x) \equiv -(sum) (\bmod N)$。

对答案的贡献就是 $f[i][j][-(sum)\% N]$。

code：

#include<cstdio>
#include<vector>
#include<cstring>
using namespace std;
const int N=15;
const int M=110;
int f[N][N][M],P;
int mod(int a,int b){ return (a%b+b)%b;}//处理负数
void init()
{
    memset(f,0,sizeof(f));//多测不清空，爆零两行泪
	for(int i=0;i<=9;i++) f[1][i][i%P]=1;
	for(int i=2;i<=10;i++)
	    for(int j=0;j<=9;j++)
	        for(int k=0;k<P;k++)
	            for(int t=0;t<=9;t++)
	                f[i][j][k]+=f[i-1][t][mod(k-j,P)];
}
int query(int n)
{
	if(!n) return 1;
	int res=0;
	vector<int>nums;
	nums.clear();
	while(n) nums.push_back(n%10),n/=10;
	int sum=0;
	for(int i=nums.size()-1;i>=0;i--)
	{
		for(int j=0;j<nums[i];j++) 
		    res+=f[i+1][j][mod(-sum,P)];
		sum+=nums[i];
		if(!i&&sum%P==0) res++; 
	}
	return res;
}
int main()
{
	int a,b;
	while(scanf("%d%d%d",&a,&b,&P)!=EOF)
	{
		init();//模数不同，所以需要多次预处理
		printf("%d\n",query(b)-query(a-1)); 
	}
	return 0;
}

不要62

不吉利的数字为所有含有 $4$ 或 $62$ 的号码。例如：$62315,73418,88914$ 都属于不吉利号码。但是，$61152$ 虽然含有 $6$ 和 $2$，但不是连号，所以不属于不吉利数字之列。

给出 $n,m$，求在 $[n,m]$ 不含有不吉利的数的个数。

数据范围

$1 \leq n \leq m \leq 10^9$

思路

定义 $f[i][j]$ 表示位数为 $i$，最高位为 $j$ 的不含有不吉利的数的的个数。得到状态转移方程：

$f[i][j]=\sum_{k=0}^{9} f[i-1][k](j \ne 4,k \ne 4,j*10+k\ne62)$。

其他的步骤就和上面差不多了。。。所以其实数位 DP 的套路基本上都一样。

code：

#include<vector>
#include<cstdio>
using namespace std;
const int N=15;
int f[N][N],a,b;
void init()
{
	for(int i=0;i<=9;i++)
	    if(i!=4) f[1][i]=1;
	for(int i=1;i<=10;i++)
	    for(int j=0;j<=9;j++)
	    {
	    	if(j==4) continue;
	    	for(int k=0;k<=9;k++)
	    	{
	    		if(k==4||j*10+k==62) continue;
	    		f[i][j]+=f[i-1][k];
			}
		}
}
int query(int n)
{
	if(!n) return 1;
	vector<int> nums;
	nums.clear();
	while(n) nums.push_back(n%10),n/=10;
	nums.push_back(114514);//不影响最高位 
	int res=0;
	for(int i=nums.size()-2;i>=0;i--)
	{
		for(int j=0;j<nums[i];j++)
	    {
	    	if(j==4||nums[i+1]*10+j==62) continue;
	    	res+=f[i+1][j];
		}
		if(nums[i+1]*10+nums[i]==62||nums[i]==4) break;
		if(!i) res++;
	}
	return res;
}
int main()
{
	init();
	while(scanf("%d%d",&a,&b),a||b) printf("%d\n",query(b)-query(a-1));
	return 0;
}

恨7不成妻

如果一个整数符合下面三个条件之一，那么我们就说这个整数和 $7$ 有关：

1.整数中某一位是 $7$；

2.整数的每一位加起来的和是 $7$ 的整数倍；

3.这个整数是 $7$ 的整数倍。

求一个区间内和 $7$ 无关的整数的平方和。

数据范围

$1 \leq T \leq 50$,

$1 \leq L \leq R \leq 10^{18}$

思路

本题的限制条件特别多，对于第一个条件显然很容易限制，而对于后面两个条件，就有一些繁琐了。

设 $f[i][j][a][b]$ 表示位数为 $i$，最高位的数为 $j$，这个数本身对 $7$ 取模等于 $a$。这个数各个数位上之和对 $7$ 取模等于 $b$ 的所有数的平方和。

那么所有可以转移的状态就是 $f[i-1][k][(a-j*10^{i-1})\%7][(b-j)\%7]$。

设这些转移的数分别为 $A_1,A_2,\dots,A_t$。

那么转移就是 $f[i][j][a][b]=\sum_{k=1}^{t}(j*10^{i-1}+A_k)^2$。

展开，得到 $(j*10^{i-1})^2*t+2*j*10^{i-1}*\sum_{k=1}^{t}A_k+\sum_{k=1}^{t}A_k^2$。

同理，一次方和为：

$\sum_{k=1}^{t}(j*10^{i-1}+A_k)=t*j*10^{i-1}+\sum_{k=1}^{t}A_k$。

所以，如果把 $t$ 看成 $A_k$ 的 $0$ 次方之和，$f$ 中需要记录的就是 $A_k$ 的 $0,1,2$ 次方。

然后就到了激动人心的填数环节。

设当前填的是第 $i$ 位，前面填的数是 $last_a=\overline{xyz}$，前面填的各个数位之和是 $last_b=x+y+z$。那么当前位 $j$ 和前面的 $a$ 以及 $b$ 就需要满足：

1.$(last_a*10^{i}+j*10^{i-1}+a)\bmod 7 \ne0$。

2.$(last_b+j+b)\bmod 7\ne 0$。

对两个式子移项，得到：

1.$(j*10^{i-1}+a) \mod 7\ne -(last_a*10^i)\bmod 7$。

2.$(j+b)\bmod 7\ne -(last_b) \bmod 7$。

最后就可以愉快地写代码了。

#include<cstdio>
#include<vector>
using namespace std;
#define int long long
const int N=25;
const int p=1e9+7;
struct node{
	int s0,s1,s2;
}f[N][10][7][7];
int l,r;
int p7[N],p9[N];//10^i 对7取模，对1e9+7取模 
int mod(int a,int b){return (a%b+b)%b;}//处理负数取模 
void init()
{
	p7[0]=p9[0]=1;
	for(int i=1;i<N;i++) p7[i]=p7[i-1]*10%7,p9[i]=p9[i-1]*10ll%p;
	for(int i=0;i<=9;i++)
	{
		if(i==7) continue;
		f[1][i][i%7][i%7].s0++;f[1][i][i%7][i%7].s1+=i;f[1][i][i%7][i%7].s2+=i*i;
	}
	for(int i=2;i<N;i++)
	    for(int j=0;j<=9;j++)
	    {
	    	if(j==7) continue;
	    	for(int a=0;a<7;a++)
	            for(int b=0;b<7;b++)
	            {
	                for(int k=0;k<=9;k++)
	                {
	                	if(k==7) continue;
	                	node &v1=f[i][j][a][b],&v2=f[i-1][k][mod(a-j*p7[i-1],7ll)][mod(b-j,7ll)];
	                	v1.s0=(v1.s0+v2.s0)%p;
	                	v1.s1=(v1.s1+p9[i-1]*v2.s0%p*j%p+v2.s1)%p;
	                	v1.s2=(v1.s2+j*p9[i-1]%p*j%p*p9[i-1]%p*v2.s0%p+2ll*j*p9[i-1]%p*v2.s1%p+v2.s2)%p;
					}
	            }
	                
		}
	        
}
node get(int i,int j,int a,int b)//注意这里是不等于a,b 
{
	node tmp;
	tmp.s0=tmp.s1=tmp.s2=0;
		for(int x=0;x<7;x++)
		{
			if(x==a) continue;
			for(int y=0;y<7;y++)
			{
				if(y==b) continue;
				tmp.s0=(tmp.s0+f[i][j][x][y].s0)%p;
				tmp.s1=(tmp.s1+f[i][j][x][y].s1)%p;
				tmp.s2=(tmp.s2+f[i][j][x][y].s2)%p;
			}
		}
	return tmp;
}
int query(int n)
{
	if(!n) return 0;
	vector<int> nums;
	nums.clear();
	while(n) nums.push_back(n%10),n/=10;
	int last_a=0,last_b=0,res=0;
	for(int i=nums.size()-1;i>=0;i--)
	{
		for(int j=0;j<nums[i];j++)
		{
		    if(j==7) continue;
			int a=mod(-last_a*p7[i+1],7ll);
			int b=mod(-last_b,7ll);
			node v=get(i+1,j,a,b);
			res=(res+(last_a%p)*(last_a%p)%p*p9[i+1]%p*p9[i+1]%p*v.s0%p+last_a%p*v.s1%p*p9[i+1]%p*2ll%p+v.s2)%p;//注意相乘顺序，不然很容易溢出
		}
		if(nums[i]==7) break;
		last_a=last_a*10ll+nums[i];
		last_b+=nums[i];
		if(!i&&last_a%7&&last_b%7)
		{
			last_a%=p;
			res=(res+last_a*last_a%p)%p;
		}
	}
	return res;
}
signed main()
{
	init();
	int T;scanf("%lld",&T);
	while(T--) scanf("%lld%lld",&l,&r),printf("%lld\n",mod(query(r)-query(l-1),p));
	return 0;
}