四边形不等式优化 dp 学习笔记
N 总发现并证明的不等式就是巧妙。
前置芝士:四边形不等式
定义
设 \(W(x,y)\) 是定义在整数集合上的二元函数。若对于定义域上的任意整数 \(a,b,c,d\),其中 \(a \leq b \leq c \leq d\),都有 \(W(a,d)+W(b,c) \geq W(a,c)+W(b,d)\) 成立(对于四个整数的大小关系,可以简单记忆为“交叉小于包含”),则称函数 \(W\) 满足四边形不等式。
定理(四边形不等式的另一种定义)
设 \(W(x,y)\) 是定义在整数集合上的二元函数。若对于定义域上的任意整数 \(a,b\),其中 \(a<b\),都有 \(W(a,b+1)+W(a+1,b) \geq W(a,b)+W(a+1,b+1)\) 成立,则函数 \(W\) 满足四边形不等式。
从上往下推很简单,只需要用 \(a+1\) 和 \(b+1\) 替换上面的 \(b\) 和 \(d\),将 \(b\) 改成 \(c\),就是上面的式子。下面简单证明一下如何由下往上推:
对于 \(a<c\),有 \(W(a,c+1)+W(a+1,c) \geq W(a,c)+W(a+1,c+1)\)。
对于 \(a+1<c\),有 \(W(a+1,c+1)+W(a+2,c) \geq W(a+1,c)+W(a+2,c+1)\)。
两式相加,得到 \(W(a,c+1)+W(a+2,c) \geq W(a,c)+W(a+2,c+1)\)。
以此类推,对于任意的 \(a \leq b \leq c < c+1\),有 \(W(a,c+1)+W(b,c) \geq W(a,c)+W(b,c+1)\)。
同理,令 \(c=c+1\),对于 \(a \leq b \leq c+1 < c+2\),列出不等式,与上式相加,得到 \(W(a,c+2)+W(b,c) \geq W(a,c)+W(b,c+2)\)。
以此类推,对于 \(a \leq b \leq c \leq d\),都有 \(W(a,d)+W(b,c) \geq W(a,c)+W(b,d)\)。
得证。
故两个式子等价。
一维线性 DP 的四边形不等式优化
对于形如 $f[i]=\min_{0 \leq j < i}{(f[j]+val(j,i))} $ 的状态转移方程,记 \(p[i]\) 为令 \(f[i]\) 取到最小值的 \(j\) 的值,则 \(p[i]\) 是 \(f[i]\) 的最优决策。若 \(p\) 在 \([1,N]\) 上非严格单调递增,则称 \(f\) 具有决策单调性。
定理(决策单调性)
若 \(p\) 对于 \(i\),\(\forall j \in [0,p-1]\),都有决策 \(p\) 比 \(j\) 更优(决策 \(p\) 不一定为最优决策,即任意决策都具有单调性)。若函数 \(val\) 满足四边形不等式,则对于 \(\forall i'>i\),都有决策 \(p\) 比 \(j\) 更优。
证明:
由上面的关系可以得到 \(0 \leq j <p <i <i'\)。
根据 \(p\) 比决策 \(j\) 更优,可以得到不等式:
\(f[p]+val(p,i) \leq f[j]+val(j,i)\)--------①。
又 \(\because\) 函数 \(val\) 满足四边形不等式,得:
\(val(j,i')+val(p,i) \geq val(j,i)+val(p,i')\)。
移项,得:
\(val(p,i')-val(p,i) \leq val(j,i')-val(j,i)\)-----②。
① \(+\) ②,得:
\(f[p]+val(p,i') \leq f[j]+val(j,i')\)。
显然,不等式的左右两边都是 \(f[i']\) 的一个决策点。故决策 \(p\) 比 \(j\) 更优。换言之,\(f[i']\) 的最优决策不可能小于 \(p\)。特别的,当 \(p\) 为 \(i\) 的最优决策,即 \(p[i]\) 时,可以得到 \(p[i'] \geq p[i]\)。所以 \(f\) 具有决策单调性。
得证。
当 \(f\) 有决策单调性时,就可以把形如 \(f[i]=\min_{0 \leq j < i}{(f[j]+val(j,i))}\) 的计算时间从 \(O(N^2)\) 优化到 \(O(N \log N)\)。
由上面的定理可以得到 \(\forall i'>i,p[i'] \geq p[i]\)。也就是 \(P\) 非严格单调递增。
初始时,\(P\) 中全部为 \(0\)。在 \(i\) 循环的任意时刻,如果已经求出了 \(p[i]\),那么就可以直接令 \(f[i]=p[i]+val(i,j)\)。而求出了 \(f[i]\) 之后, \(i\) 也就有可能去更新其他状态。于是就用 \(i\) 来更新 \(p\) 数组。
若 \(p\) 中某一位置取到 \(i\) ,那么后面的所有位置都为 \(i\),因为当前最大的值就是 \(i\),而 \(p\) 数组又满足非严格单调递增,后面的值都要 \(\geq i\),那么后面的值就自然都为 \(i\) 了。
而要快速找到第一个取 \(i\) 的点的下标,显然可以用二分查找。
而一个个修改显然效率太低了。因为 \(p\) 数组满足非严格单调递增,所以可能存在一段很长的子区间,在这个子区间内 \(p\) 的值都相同(通过上面的修改操作也可以发现)。那么就可以建立一个队列来代替 \(p\) 数组。队列中保持若干个三元组 \((l,r,j)\),表示 \(p\) 在 \([l,r]\) 内的取值都为 \(j\)。
对于修改操作,就可以从队尾开始查找,如果发现当前区间的开头填 \(i\) 更优,那么直接删去就可以;如果发现当前区间的开头不应该填 \(i\),那么判断区间的结尾是否应该填 \(i\),如果结尾填 \(i\) 更优,那么就说明这个区间可以分为两部分,前面的部分保持不变,后面的部分改为 \(i\) 即可。而找到这个区间的分界点就可以用二分查找。
可以发现,每个区间最多被删除一次,删除只需 \(O(1)\),每次查找的时间下界为 \(O(\log N)\)。所以每一次修改的瓶颈就是 \(O(\log N)\),
而一旦求完 \(i\),由于 \(i\) 之后的决策点一定 \(\geq p[i]\),那么队列中所有小于 \(p[i]\) 的区间就没有用了,直接删除即可。那么把所有不会用到的 \(p\) 删去以后,队列的开头就是当前节点的最优决策点了(类似于单调队列)。后面会给出具体代码。
例题 [NOI2009] 诗人小G
题意
给出若干个句子,将这些句子按顺序排成若干行,给出一个期望长度 \(L\) 和一个整数 \(P\),设第 \(i\) 行句子(包括标点)的总长度为 \(x\),那么第 \(i\) 行的不和谐度就为 \(|x-L|^P\)。求一个方案使得句子的总不和谐度最小,并输出这个方案。
思路
设 \(f[i]\) 表示对前 \(i\) 句诗排版的最小不和谐度,记 \(a[i]\) 为第 \(i\) 句诗的长度,\(sum[i]\) 为前 \(i\) 句诗的总长度。得:
\(f[i]=\min_{0 \leq j < i}(f[j]+|(sum[i]-sum[j])+(i-j-1)-L|^P)\)。
可以发现,题目中的 \(P\) 就是用来防止单调队列优化或斜率优化的。于是可以令 \(val(i,j)=(f[j]+|(sum[i]-sum[j])+(i-j-1)-L|^P)\)。尝试判断 \(val\) 是否满足四边形不等式。
也就是要证明:
\(\forall j<i\),满足 \(val(j,i+1)+val(j+1,i) \geq val(j,i)+val(j+1,i+1)\)。
只需证明: \(val(j+1,i)-val(j+1,i+1) \geq val(j,i)-val(j,i+1)\)。
令 \(u=(sum[i]-sum[j])+(i-j-1)-L\)。
令 \(v=(sum[i]-sum[j+1])+(i-(j+1)-1)-L\)。
只需证明 \(|v|^p-|v+(a[i+1]+1)|^p \geq |u|^p-|u+(a[i+1]+1)|\)。
显然 \(u>v\)。故只需证明,对于任意正整数 \(c\),函数 \(y=|x|^p-|x+c|^p\) 非严格单调递减。接下来对于 \(p \in [1.10]\) 的奇偶性和 \(x\) 的范围分类讨论:
1.\(p\) 为偶数。\(y=x^p-(x+c)^p\)。对 \(x\) 求导,得 \(y'=px^{p-1}-p(x+c)^{p-1}\),显然 \(x^{p-1}\) 单调递增。而 \((x+c)^{p-1} \geq x^{p-1}\),\(p \geq 2\),故 \(y'\leq 0\)。
2.\(p\) 为奇数,且 \(x \in [-c,0]\) 时。\(y=-x^p-(x+c)^p\)。对 \(x\) 求导,得 \(y'=-p*x^{p-1}-p*(x+c)^{p-1}\)。因为 \(p-1\) 为偶数,\(p\) 是正整数,所以 \(y'\leq 0\)。
3.\(p\) 为奇数,且 \(x \in (-\infty,c)\) 时。\(y=-x^p+(x+c)^p,y'=-px^{p-1}+p(x+c)^{p-1}\)。而 \(|x| \geq |x+c|\),故 \(p*(x+c)^{p-1} \leq p*x^{p-1}\)。所以 \(y' \geq 0\)。
4.\(p\) 为奇数,且 \(x \in (0,\infty)\) 时。\(y=x^p-(x+c)^p,y'=px^{p-1}-p*(x+c)^{p-1}\)。因为 \(p-1\) 为奇数,故 \(x^{p-1}\) 在 \(x \in (0,\infty)\) 时单调递增。故 \(p*x^{p-1} \leq p*(x+c)^{p-1}\)。故 $ y' \leq 0$。
故函数 \(y=|x|^p-|x+c|^p\) 非严格单调递减。
因此,\(val\) 满足四边形不等式。上面的状态转移方程就可以用决策单调性优化。
最后需要注意一下本题中的数据范围,最小的不和谐度也可能超过 \(10^{18}\),所以需要开 long double。
code:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define LD long double
const int N=1e5+10;
int T,n,l,p,s[N],opt[N],hh,tt;
struct node{
int l,r,j;
}q[N];
LD f[N];
char str[N][40];
LD val(int j,int i)
{
LD res=1,a=abs((s[i]-s[j])+(i-j-1)-l);
for(int i=1;i<=p;i++) res*=a;
return res+f[j];
}
void insert(int i)
{
int pos=n+1;
while(hh<=tt&& val(q[tt].j,q[tt].l)>=val(i,q[tt].l)) pos=q[tt--].l;
if(hh<=tt&&val(q[tt].j,q[tt].r)>=val(i,q[tt].r)) //如果当前区间的左端点是j更优,右端点是i更优
{
int l=q[tt].l,r=q[tt].r;
while(l<r)
{
int mid=(l+r)>>1;
if(val(q[tt].j,mid)>=val(i,mid)) r=mid;
else l=mid+1;
}
q[tt].r=r-1;//因为查找的r是第一个i更优的,那么j更优的就在r-1
pos=r;
}
if(pos!=n+1) q[++tt]=node{pos,n,i};
}
int main()
{
scanf("%d",&T);
while(T--)
{
scanf("%d%d%d",&n,&l,&p);
for(int i=n;i>=1;i--) scanf("%s",str[i]);//便于输出答案
for(int i=1;i<=n;i++) s[i]=s[i-1]+strlen(str[i]);
hh=0,tt=0;
q[0]=node{1,n,0};
for(int i=1;i<=n;i++)
{
f[i]=val(q[hh].j,i),opt[i]=q[hh].j;
if(q[hh].r==i) hh++;//如果当前这一段决策最多只能作为i的最优决策点,那么i以后的点也就不需要这段最优决策了
q[hh].l=i+1;//只需要关注后面没赋值的点即可
insert(i);
}
if(f[n]>1e18) puts("Too hard to arrange");
else
{
printf("%lld\n",(long long)f[n]);
for(int i=n;i;i=opt[i])
{
for(int j=i;j>opt[i];j--)
{
printf("%s",str[j]);
if(j!=opt[i]+1) printf(" ");
}
puts("");
}
}
puts("--------------------");
}
return 0;
}
二维线性 DP 的四边形不等式优化
定理
在状态转移方程 \(f[i][j]=\min_{i \leq k <j}(f[i][k]+f[k+1][j]+w(i,j))\) 中(特别地,\(f[i][i]=w(i,i)=0\)),如果下面两个条件成立:
- \(w\) 满足四边形不等式。
2.对于任意的 \(a \leq b \leq c \leq d\),有 \(w(a,d) \geq w(b,c)\)。
那么 \(f\) 也满足四边形不等式。
证明:
\(f[i][i+1]=f[i][i]+f[i+1][i+1]+w(i,i+1)=w(i,i+1)\)。(区间 \([i,i+1]\) 的决策点只能是 \(i\))
当 \(i+1=j\) 时,\(f[i][j+1]+f[i+1][j]=f[i][i+2]+f[i+1][i+1]=f[i][i+2]\)。
此时 \(f[i][i+2]\) 的最优决策点的取值只有 \(i\) 和 \(i+1\)。下面对取值进行分类讨论:
若 \(f[i][i+2]\) 的最优决策是 \(i\),则 \(f[i][i+2]=f[i][i]+f[i+1][i+2]+w(i,i+2)=w(i,i+2)+w(i+1,i+2) \geq w(i,i+1)+w(i+1,i+2)=f[i][i+1]+f[i+1][i+2]=f[i][j]+f[i+1][j+1]\)。
若 \(f[i][i+2]\) 的最优决策是 \(i+1\),则 \(f[i][i+2]=f[i][i+1]+f[i+2][i+2]+w(i,i+2)=w(i,i+1)+w(i,i+2) \geq w(i,i+1)+w(i+1,i+2)=f[i][i+1]+f[i+1][i+2]=f[i][j]+f[i+1][j+1])\)。
而根据最上面的等式,就可以得到:
\(f[i][i+2]=f[i][i+2]+f[i+1][i+1]=f[i][j+1]+f[i+1][j] \geq f[i][j]+f[i+1][j+1]\)。
故当 \(i+1=j\) 时,四边形不等式对 \(f[i][j]\) 成立。
接下来,用数学归纳法,假设当 \(j-i<k\) 时,四边形不等式对 \(f(i,j)\) 成立。考虑 \(j-i=k\) 的情况。设 \(f[i][j+1]\) 以 \(x\) 为最优决策,\(f[i+1][j]\) 以 \(y\) 为最优决策。接下来对 \(x\) 和 \(y\) 的大小关系进行分类讨论:
①.若 \(i \leq x \leq y <j\),同时也有 \(i \leq x \leq j,i+1\leq y < j\),
\(f[i][j+1]+f[i+1][j]=f[i][x]+f[x+1][j+1]+w(i,j+1)+f[i+1][y]+f[y+1][j]+w(i+1,j)\)。
同时 \(x\) 在 \(f[i][j]\) 的决策范围内,\(y\) 在 \(f[i+1][j+1]\) 的决策范围内,那么 \(x,y\) 均可以作为一个决策(不一定是最优决策),就可以得到:
\(f[i][j]+f[i+1][j+1] \leq f[i][x]+f[x+1][j]+w(i,j)+f[i+1][y]+f[y+1][j+1]+w(i+1,j+1)\)
同时因为 \(w\) 满足四边形不等式,就可以得到:
\(i<i+1 \leq j < j+1\),\(w(i,j+1)+w(i+1,j) \geq w(i,j)+w(i+1,j+1)\)。
现在只需要证明:
\(f[i][x]+f[x+1][j+1]+f[i+1][y]+f[y+1][j] \geq f[i][x]+f[x+1][j]+f[i+1][y]+f[y+1][j+1]\)。
发现两边有相同项,可以消去,于是就只需证:
\(f[x+1][j+1]+f[y+1][j] \geq f[x+1][j]+f[y+1][j+1]\)。
根据归纳假设,\(x+1 \leq y+1 \leq j < j+1\),满足 \(j-(x+1) <j-i=k\),那么就可以得到:
\(f[x+1][j+1]+f[y+1][j] \geq f[x+1][j]+f[y+1][j+1]\)。
整理一下上面的式子,就可以得到:
\(f[i][j+1]+f[i+1][j]=f[i][x]+f[x+1][j+1]+w(i,j+1)+f[i+1][y]+f[y+1][j]+w(i+1,j) \geq f[i][x]+f[x+1][j]+w(i,j)+f[i+1][y]+f[y+1][j+1]+w(i+1,j+1) \geq f[i][j]+f[i+1][j+1]\)。
情况 ① 得证。
②.若 $i+1 \leq y \leq x \leq j $,就有 \(i+1 \leq x \leq j,i+1 \leq y <j\)。
根据 \(x\) 是 \(f[i][j+1]\) 的最优决策,\(y\) 是 \(f[i+1][j]\) 的最优决策,可以得:
\(f[i][j+1]+f[i+1][j]=f[i][x]+f[x+1][j+1]+w(i,j+1)+f[i+1][y]+f[y+1][j]+w(i+1,j)\)。
而 \(x\) 在 \(f[i+1][j+1]\) 的决策范围内,\(y\) 在 \(f[i][j]\) 的决策范围内,可以得:
\(f[i][j]+f[i+1][j+1] \leq f[i][y]+f[y+1][j]+w(i,j)+f[i+1][x]+f[x+1][y+1]+w(i+1,j+1)\)。
只需证明:
\(f[i][x]+f[x+1][j+1]+w(i,j+1)+f[i+1][y]+f[y+1][j]+w(i+1,j) \geq f[i][y]+f[y+1][j]+w(i,j)+f[i+1][x]+f[x+1][j+1]+w(i+1,j+1)\)。
因为 \(w\) 满足四边形不等式,得:
\(i<i+1 \leq j < j+1\),\(w(i,j+1)+w(i+1,j) \geq w(i,j)+w(i+1,j+1)\)。
消去不等式左右两边的 \(w\),以及相同项,只需证:
\(f[i][x]+f[i+1][y] \geq f[i][y]+f[y+1][j]\)。
根据情况假设,可以得到 \(y \leq x \leq j\)。
1.\(i < i+1 \leq y\leq x \leq j <\)。\(\because j-i =k\),\(\therefore x-(i+1) \leq k-1 < k\)。根据归纳假设,得:
$i <i+1 \leq y \leq x \(,\)f[i][x]+f[i+1][y] \geq f[i][y]+f[i+1][x]$。
整理式子,最终可得:
\(f[i][j+1]+f[i+1][j]=f[i][x]+f[x+1][j+1]+w(i,j+1)+f[i+1][y]+f[y+1][j]+w(i+1,j) \geq f[i][y]+f[y+1][j]+w(i,j)+f[i+1][x]+f[x+1][j+1]+w(i+1,j+1)=f[i][j]+f[i+1][j+1]\)。
得证。
定理:二维决策单调性
在状态转移方程\(f[i][j]=\min_{i \leq k <j}(f[i][k]+f[k+1][j]+w(i,j))\) 中(特别地,\(f[i][i]=w(i,i)=0\)),记 \(p[i][j]\) 为令 \(f[i][j]\) 取到最小值的 \(k\) 的值。
如果 \(f\) 满足四边形不等式,那么对于任意 \(i<j\),有 \(p[i][j-1] \leq p[i][j] \leq p[i+1][j]\).
证明:
记 \(p=p[i][j]\),对于任意的 \(i<i+1 \leq k \leq p\),因为 \(F\) 满足四边形不等式:
\(f[i][p]+f[i+1][k] \leq f[i][k]+f[i+1][p]\)。
移项,得:
\(f[i+1][k]-f[i+1][p] \leq f[i][k]-f[i][p]\)。
根据 \(p\) 的最优性,得:
\(f[i][k]+f[k+1][j+1] \geq f[i][q]+f[q+1][j+1]\)。
在 \(f[i+1][j]\) 中任取 \(k \leq q\),让两个决策点相减,得:
\((f[i+1][k]+f[k+1][j]+w(i+1,j))-(f[i+1][q]+f[q+1][j]+w(i+1,j))\)
\(=(f[i+1][k]-f[i+1][q])+(f[k+1][j]-f[q+1][j])\)
\(\geq (f[i][k]-f[i][p])+(f[k+1][j]-f[q+1][j])\)
\(=(f[i][k]+f[k+1][j])-(f[i][p]+f[q+1][j])\)
\(\geq 0\)
那么就意味着,对于 \(f[i+1][j]\),\(p\) 比之前的任意 \(k\) 更优。因此 \(p[i+1][j] \geq p[i][j]\)。同理可以证得 \(p[i][j-1] \leq p[i][j]\)。
得证。
例题 再探石子合并
题意
和简化版的题意一样,只不过本题中,\(n \leq 5000\)。
思路
首先令 \(s\) 表示石子个数的前缀和,可以得到朴素的状态转移方程:
\(f[i][j]=\min_{i\leq k <j}(f[i][k]+f[k+1][j]+s[j]-s[i-1])\)。
如果用 \(w(i,j)\) 来替换 \(s[j]-s[i-1]\),那么本题就完全是四边形不等式优化的模板题了。
而在枚举 \(f[i][j]\) 时,区间长度 \(<(j-i+1)\) 的区间必然已经被搜过了,那么这些区间的决策点也就必然知道,那么根据上面证明的定理:
\(p[i][j-1] \leq p[i][j] \leq p[i+1][j]\)。
\(k\) 的范围就可以控制在区间 \([p[i][j-1],p[i+1][j]]\) 中了。这样的时间复杂就可以优化到 \(O(n^2)\)。
下面简单证明一下时间复杂度:
对于区间 \([i,j]\),一共循环了 \(p[i+1][j]-p[i][j-1]+1\) 次,下图统计了在 \(n=5\) 时,\(p[i][j]\) 的加减情况:
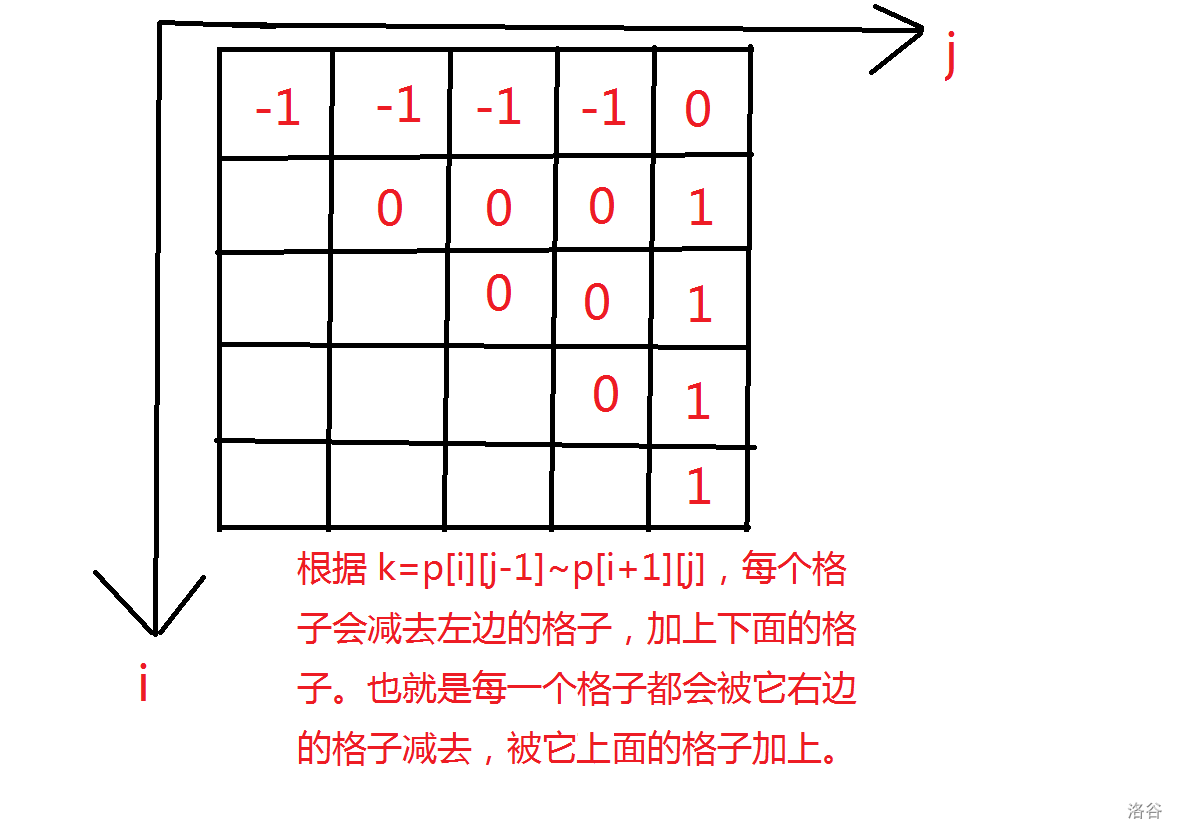
算法的时间复杂度为 \(O( {\textstyle \sum_{i=1}^{N-1}}(p[l+1,N]-P[1,N-l]+N-l))=O(N^2)\)。
code:
#include<cstdio>
using namespace std;
const int N=5050;
const int INF=0x3f3f3f3f;
int f[N][N],s[N],n,p[N][N];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&s[i]);
s[i]+=s[i-1];
p[i][i]=i;
}
for(int len=2;len<=n;len++)
for(int l=1;l<=n;l++)
{
int r=l+len-1;
f[l][r]=INF;
for(int k=p[l][r-1];k<=p[l+1][r];k++)
{
if(f[l][k]+f[k+1][r]+s[r]-s[l-1]<=f[l][r])
{
f[l][r]=f[l][k]+f[k+1][r]+s[r]-s[l-1];
p[l][r]=k;
}
}
}
printf("%d\n",f[1][n]);
return 0;
}
总结
事实上,如果在考试时遇到了状态转移方程很简单,但时间复杂度不对的状态转移方程,如果这个状态转移方程即无法分离常数,也无法用斜率优化或其他优化。就可以考虑四边形不等式优化。但不需要证明,因为太浪费时间了。可以先在朴素的转移中记录决策点,然后输出,观察决策点是否非严格单调递增(一维和二维不同),如具有单调性就大概率可以用决策单调性优化(其实就是打表找规律)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号