平衡树 Treap 学习笔记
应该是目前提高级大纲里面最难的数据结构了。。。
前置芝士:BST
给定一棵二叉树,树上的每个节点带有一个数值,称为节点的“关键码”。所谓的“BST 性质”是指,对于树中的任意一个节点:
1.该节点的关键码不小于它的左子树中任意节点的关键码。
2.该节点的关键码不大于它的右子树中任意节点的关键码。
满足上述性质的二叉树就算一棵“二叉查找树”(BST)。显然,二叉查找树的中序便利是一个关键码非严格单调递增的节点序列。
BST 的建立
为了避免越界,减少边界情况的特殊判断,我们一般在 BST 中额外插入一个关键码为正无穷和一个关键码为负无穷的节点。
同时别忘了考虑有多个相同的数的情况。
const int N=1e5+10;
struct BST{
int l,r;//左右儿子的下标
int val;//节点关键码
int cnt,size;//关键码相同的节点的数量,子树大小
}tr[N];
int push_up(int p){tr[p].size=tr[tr[p].l].size+tr[tr[p].r].size+tr[p].cnt;}
int newnode(int val)
{
tr[++num].val=val
tr[num].cnt=tr[num].size=1;
return tot;
}
void build()
{
newnode(-INF),newnode(INF);
root=1,tr[1].r=2;
push_up(root);
}
BST的查找
在 BST 中查找是否存在关键码为 \(val\) 的节点。
设变量 \(p=root\),执行以下过程:
1.若 \(p\) 的关键码等于 \(val\),则已经找到。
2.若 \(p\) 的关键码大于 \(val\)
(1)若 \(p\) 的左儿子为空,那么就不存在 \(val\)。
(2)若 \(p\) 的左子节点不为空,在 \(p\) 的左子树中递归进行搜索。
3.若 \(p\) 的关键码小雨 \(val\)
(1)若 \(p\) 的右儿子为空,那么就不存在 \(val\)。
(2)若 \(p\) 的右子节点不为空,在 \(p\) 的右子树中递归进行搜索。
int get(int p,int val)
{
if(p==0) return 0;//不存在
if(val==tr[p].val) return p;//找到了
return val<tr[p].val?get(tr[p].l,val):get(tr[p].r,val);
}
BST 的插入
在 BST 中插入一个新的值 \(val\)。
与 BST 的查找类似。
如果发现当前节点的儿子 \(p\) 为空,直接建立一个关键码为 \(val\) 的新节点作为 \(p\) 的子节点。
void insert(int &p,int val)//注意此时的p是父节点的儿子,更新p的同时也会更新父节点的儿子
{
if(p==0)
{
p=newnode(val);
return ;
}
if(val==tr[p].val)
{
tr[p].cnt++,push_up(p);
return ;
}
else if(val<tr[p].val) insert(tr[p].l,val);
else insert(tr[p].r,val);
push_up(p);//别忘了更新当前节点的信息
}
BST 求前驱/后继
这里以“后继”为例。\(val\) 的“后继”为 BST 中关键码大于 \(val\) 的前提下,关键码最小的节点。
初始化 \(ans\) 为具有正无穷关键码的那个节点的编号。然后,在 BST 中搜索 \(val\)。在搜索过程中,每经过一个节点,都检查该节点的关键码,判断是否在满足 大于 \(val\) 的前提下更小的节点。并更新 \(ans\)。
搜索完成后,有三种可能的结果:
1.没有找到 \(val\)。此时的 \(val\) 的后继就在已经经过的节点中,\(ans\) 即为 \(val\) 的后继。
2.找到了关键码为 \(val\) 的节点 \(p\),但 \(p\) 不存在右子树。那么根据 BST 性质,路径上经过的最小值 \(ans\) 即为 \(val\) 的后继。
3.找到了关键码为 \(val\)的节点 \(p\),且 \(p\) 有右子树。那么根据 BST 性质, \(p\) 的右子树中的节点的关键码都大于 \(val\)。在右子树中一直向左走就能找到 \(val\) 的后继。
int get_next(int val)
{
int ans=2;//tr[2].val=INF
int p=root;
while(p)
{
if(val==tr[p].val)
{
if(tr[p].r>0)
{
p=tr[p].r;
while(tr[p].l>0) p=tr[p].l;
ans=p;
}
break;
}
if(tr[p].val>val&&tr[p].val<tr[ans].val) ans=p;//更新答案
p=val<tr[p].val?tr[p].l:tr[p].r;
}
return ans;
}
BST 的删除
从 BST 中删除关键码为 \(val\) 的节点。
首先,在 BST 中查找 \(val\),得到节点 \(p\)。
若 \(p\) 的子节点个数小于 \(2\),则直接删除 \(p\),并令 \(p\) 的子节点代替\(p\) 的位置,与 \(p\) 的父节点相连(如果 \(p\) 为叶子节点就只删除即可)。
若 \(p\) 的子节点个数等于 \(2\),则在 BST 中求出 \(val\) 的后继节点 \(next\)。因为 \(next\) 没有左子树(后继的定义,\(next\) 的左子树中节点的关键码一定小于等于 \(next\),但小于 \(next\) 的最小节点就是 \(p\)),所以可以直接删除 \(next\),并且令 \(next\) 的右子树代替 \(next\) 的位置。最后,再让 \(next\) 节点代替 \(p\) 节点,删除 \(p\) 即可。
void Remove(int &p,int val) //删除关键码为val的节点
{
if(p==0) return ;
if(val==tr[p].val)
{
if(tr[p].l==0) p=tr[p].r;//右子树代替p
else if(tr[p].r==0) p=tr[p].l;//左子树代替p
else
{
int nex=tr[p].r;
while(tr[nex].l>0) nex=tr[nex].l;//找到p的后继next
remove(tr[p].r,tr[nex].val);//在p的右子树中删除next,这一步是防止next代替p后出现错误
tr[nex].l=tr[p].l,tr[nex].r=tr[p].r;//令节点next直接代替节点p的位置
p=nex;//注意同时也要更新p的父节点的信息
}
}
else if(val<tr[p].val) remove(tr[p].l,val);
else remove(tr[p].r,val);
}
在随机数据中,BST一次操作的期望复杂度为 \(O(\log N)\)。然而,如果在 BST 中依次插入一个有序序列,将会得到一条链,平均每次操作的时间复杂度为 \(O(N)\)。因此 Treap 可以完全取代 BST 。
Treap
其实 Treap 的实用性也不是很大,但是不学 Treap 就学不会 splay 了。
满足 BST 性质且中序遍历为相同序列的二叉查找树时不唯一的。这些二叉查找树是等价的,它们维护的是相同的一组数值。在这些二叉查找树上执行同样的操作,将得到相同的结果。因此,我们可以在维持 BST 性质的基础上,通过改变二叉查找树的形态,使得树上每个节点的左右子树大小达到平衡,从而使整棵树的深度维持在 \(O(\log N)\) 级别。
改变形态并保持 BST 性质的方法就是“旋转”。最基本的旋转操作称为“单旋转”,它又分为“左旋”和“右旋”。如下图所示。
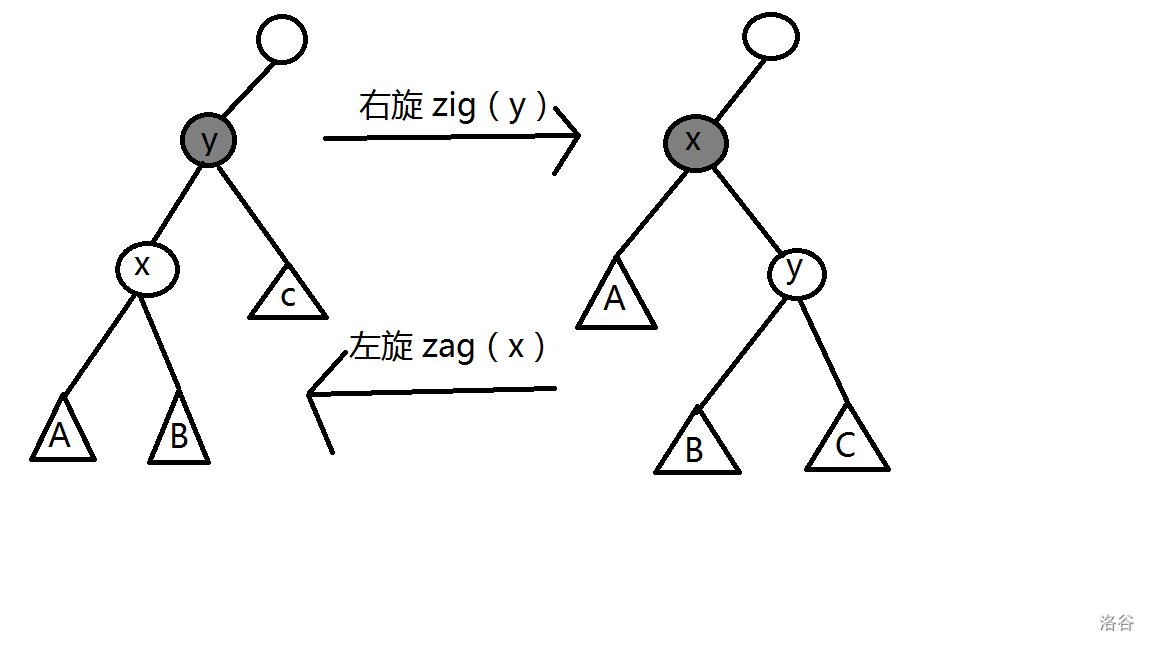
以右旋为例。在初始情况下,\(x\) 是 \(y\) 的左儿子,\(A\) 和 \(B\) 分别是 \(x\) 的左右儿子,\(C\) 是 \(y\) 的右儿子。
“右旋”操作在保持 BST 性质的基础上,把 \(x\) 变为 \(y\) 的父节点。因为 \(x\) 的关键码小于 \(y\) ,所以 \(y\) 应该是 \(x\) 的右儿子。而 \(B\) 的关键码比 \(x\) 大,同时又比 \(y\)小,所以旋转后的 \(B\) 是 \(y\) 的左儿子。
右旋操作的代码如下,\(zig(p)\) 可以理解成把 \(p\) 的左儿子绕着 \(p\) 向右转。
void zig(int &p)//将q旋转为p的父亲
{
int q=tr[p].l;
tr[p].l=tr[q].r,tr[q].r=p;//q的右儿子变成了p的左儿子,p变成了q的右儿子
p=q;//p的父节点的信息也要更新
}
左旋操作的代码如下,\(zag(p)\) 可以理解成把 \(p\) 的右儿子绕着 \(p\) 向左转。
void zag(int &p)//将p的右儿子q旋转为p的父亲
{
int q=tr[p].r;
tr[p].r=tr[q].l,tr[q].l=p;
p=q;//同上
}
合理的旋转可以使得 BST 变得更“平衡”。如下图所示,对一条形状为链的 BST 进行一系列单旋转操作后,这棵 BST 变得比较平衡了。
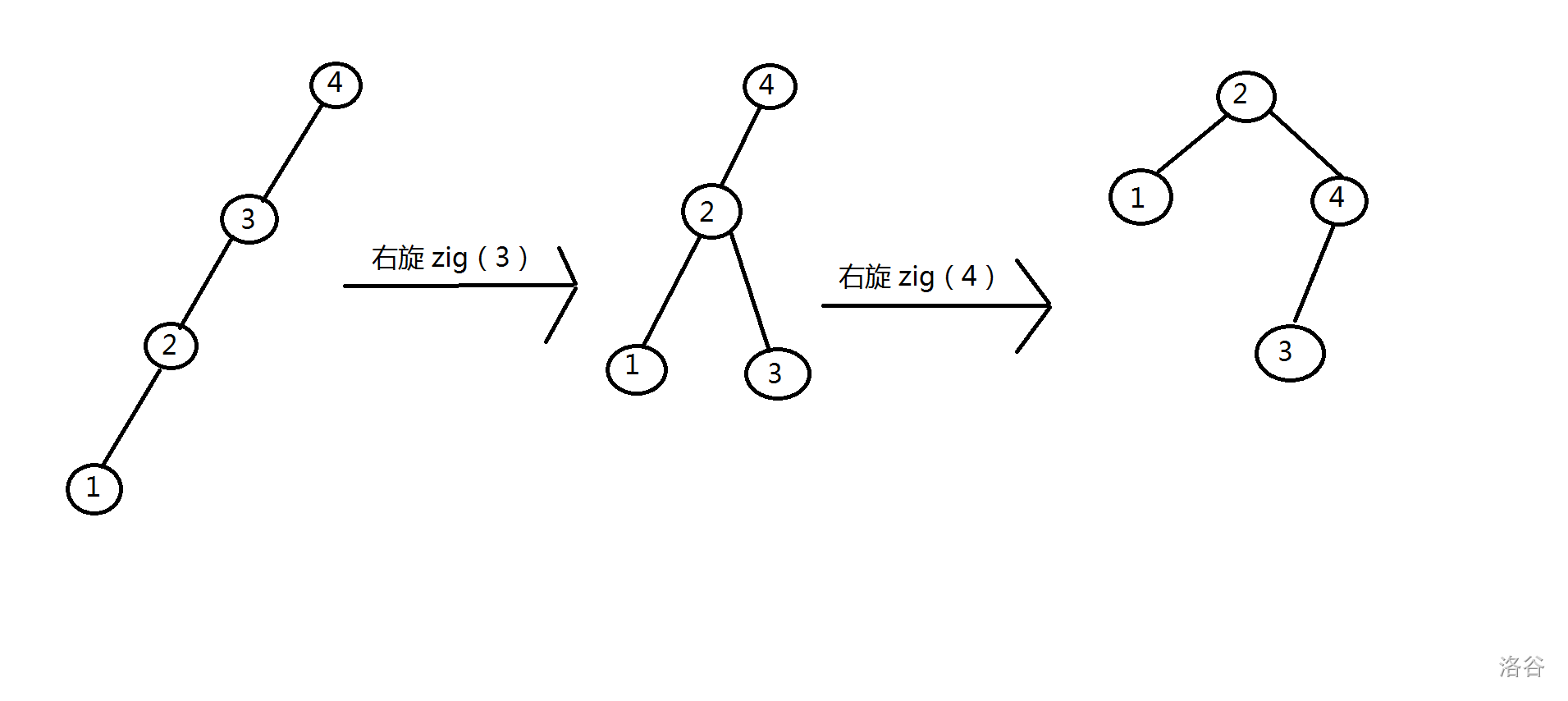
现在,问题就是,怎样才算“合理”的旋转操作呢?可以发现,在随机数据下,普通的 BST 趋于平衡。Treap 的思想就是利用“随机”在创造平衡条件。因为在旋转过程中必须维持 BST 性质,所以 Treap 就把“随机”作用在堆性质上。
Treap=Tree+heap
Treap 在插入每一个新节点时,给该节点随机生成一个额外的权值。然后像二叉堆的插入过程一样,自底向上一次检查,当某个节点不满足大根堆性质(即父节点的值不小于左右儿子的值,也就是根节点的值最大),就执行单旋转操作,使该点与其父节点的关系发生对换。
而对于删除操作,因为 Treap 支持旋转,可以直接找到需要删除的节点,并把它向下旋转成叶子节点,然后直接删除。这样就避免了普通 BST 可能带来的种种问题。
总而言之,Treap通过适当的单旋转,在维持节点关键码满足 BST 性质的同时,还使每个节点上随机生成的额外权值满足大根堆性质。故 Treap 各种操作的时间复杂度都是 \(O(\log N)\)。
(下面的题目由于选自本蒟蒻不同时期的代码,所以码风略有不同)
例题 普通平衡树
题意
写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下操作:
1.插入一个数 \(x\)。
2.删除一个数 \(x\) 数(若有多个相同的数,因只删除一个)。
3.查询 \(x\) 数的排名 (排名定义为比当前数小的数的个数 \(+1\) )。
4.查询排名为 \(x\) 的数。
5.求 \(x\) 的前驱(前驱定义为小于 \(x\),且最大的数)。
6.求 \(x\) 的后继(后继定义为大于 \(x\),且最小的数)。
思路
本题就是实现平衡树的各种操作。同时别忘了注意一下题目中可能会有相同的数。
用普通的 BST 当然是无法通过本题的。而 Treap 和普通 BST 的区别就在于插入(维护堆性质)和删除(旋转子节点)操作。
还有一些关于 Treap 的具体实现细节见代码。
code:
#include<cstdio>
#include<ctime>
#include<cstdlib>
using namespace std;
const int N=1e5+10;
const int INF=0x3f3f3f3f;
struct BST{
int l,r;//左右儿子的下标
int val,f;//节点关键码,随机值
int cnt,size;//关键码相同的节点的数量,子树大小
}tr[N];
int min(int a,int b){return a<b?a:b;}
int max(int a,int b){return a>b?a:b;}
int root,num;
int push_up(int p){tr[p].size=tr[tr[p].l].size+tr[tr[p].r].size+tr[p].cnt;}
int newnode(int val)
{
tr[++num].val=val;
tr[num].cnt=tr[num].size=1;
tr[num].f=rand();
return num;
}
void zig(int &p)//将p的左儿子q旋转为p的父亲
{
int q=tr[p].l;
tr[p].l=tr[q].r,tr[q].r=p;//q的右儿子变成了p的左儿子,p变成了q的右儿子
p=q;//p的父节点的信息也要更新
push_up(tr[p].r),push_up(p);
}
void zag(int &p)//将p的右儿子q旋转为p的父亲
{
int q=tr[p].r;
tr[p].r=tr[q].l,tr[q].l=p;
p=q;//同上
push_up(tr[p].l),push_up(p);
}
void build_tree()
{
newnode(-INF),newnode(INF);
root=1,tr[1].r=2;
push_up(root);
if(tr[1].f<tr[2].f) zag(root);//注意维护堆性质
}
int get_rank_by_val(int p,int val)
{
if(p==0) return 0;
if(val==tr[p].val) return tr[tr[p].l].size+1;//注意x的排名为比它小的数的数量+1
if(val<tr[p].val) return get_rank_by_val(tr[p].l,val);
return get_rank_by_val(tr[p].r,val)+tr[tr[p].l].size+tr[p].cnt;//注意搜索右子树时还要加上左子树和父节点的数的数量
}
int get_val_by_rank(int p,int rank)
{
if(p==0) return INF;
if(tr[tr[p].l].size>=rank) return get_val_by_rank(tr[p].l,rank);//如果在左子树中
if(tr[tr[p].l].size+tr[p].cnt>=rank) return tr[p].val;//是父节点
return get_val_by_rank(tr[p].r,rank-(tr[tr[p].l].size+tr[p].cnt));//如果在右子树中,记得排名要减去左子树和父节点数的数量,因为这是依据数的数量来算排名的
}
void insert(int &p,int val)//注意此时的p是父节点的儿子,更新p的同时也会更新父节点的儿子
{
if(p==0)
{
p=newnode(val);
return ;
}
if(val==tr[p].val)
{
tr[p].cnt++,push_up(p);
return ;
}
if(val<tr[p].val)
{
insert(tr[p].l,val);
if(tr[p].f<tr[tr[p].l].f) zig(p);//左儿子的随机值比父亲大,就把左儿子旋转上来
}
else
{
insert(tr[p].r,val);
if(tr[p].f<tr[tr[p].r].f) zag(p);//同上
}
push_up(p);//别忘了更新当前节点的信息
}
int get_next(int p,int val)//写成递归式简洁一些
{
if(!p) return INF;
if(tr[p].val<=val) return get_next(tr[p].r,val);
return min(tr[p].val,get_next(tr[p].l,val));
}
int get_pre(int p,int val)
{
if(!p) return -INF;
if(tr[p].val>=val) return get_pre(tr[p].l,val);
return max(tr[p].val,get_pre(tr[p].r,val));
}
void remove(int &p,int val) //删除关键码为val的节点
{
if(p==0) return ;
if(val==tr[p].val)
{
if(tr[p].cnt>1) tr[p].cnt--;
else if(tr[p].l||tr[p].r) //不是叶子节点
{
if(tr[p].r==0 ||tr[tr[p].l].val>tr[tr[p].r].val) zig(p),remove(tr[p].r,val);
else zag(p),remove(tr[p].l,val);
}
else p=0;//叶子节点。直接删除即可
}
else if(val<tr[p].val) remove(tr[p].l,val);
else remove(tr[p].r,val);
push_up(p);
}
int main()
{
srand((unsigned)time(0));
int n,opt,x;
build_tree();
scanf("%d",&n);
while(n--)
{
scanf("%d%d",&opt,&x);
if(opt==1) insert(root,x);//插入
else if(opt==2) remove(root,x);//删除
else if(opt==3) printf("%d\n",get_rank_by_val(root,x)-1);//根据关键码查排名,因为有一个-INF在,所以要-1
else if(opt==4) printf("%d\n",get_val_by_rank(root,x+1));//根据排名查关键码 ,同上
else if(opt==5) printf("%d\n",get_pre(root,x));//前驱
else printf("%d\n",get_next(root,x));//后继
}
}
事实上,如果把 \(p\) 的左右儿子分别用 \(son[0]\) 和 \(son[1]\) 来表示,那么就可以运用异或的技巧将 zig 和 zag用一个函数来表示:
void rotate(int &p,int d) //1右旋,0左旋
{
int q=son[p][d^1];
son[p][d^1]=son[q][d],son[q][d]=p;
p=q;
push_up(son[p][d]),push_up(p);
}
应用 挑剔的美食家
题意
有 \(n\) 头奶牛,每头奶牛都对她的牧草做出了要求:价格不能低于 \(a_i\),新鲜程度不能低于 \(b_i\)。商店里有 \(m\) 种牧草,第 \(i\) 种牧草的价格为 \(c_i\) ,新鲜程度为 \(d_i\)。 没有两头奶牛的牧草一样。求最少的花费。无解输出 \(-1\)。
思路
由于题目可能存在无解的情况,所以首先保证有解,再保证答案最小。
注意到题目中虽然有两个限制条件,但是只是要求价格之和最小,并未要求新鲜度之和最小。那么就可以先按照新鲜程度排序。优先考虑新鲜程度较大的牧草。因为它可以满足更多奶牛的要求。
同时运用贪心的思想,如果两堆牧草满足 \(d_i >d_j\),两只奶牛满足 \(b_i>b_j\) 那么显然把 \(d_i\) 给第 \(i\) 只奶牛更优。如果 \(d_i\) 可以满足两头奶牛,但是 \(d_j\) 只可以满足第 \(j\) 头奶牛,那么如果把牧草 \(i\) 给奶牛 \(j\),那么奶牛 \(j\) 就没有牧草了。
于是,可以在所有满足 \(d_j >b_i\) 的牧草中找到 \(c_j\) 最小的牧草分配给第 \(i\) 头奶牛。同时删去这种牧草。
可以发现,上述思路要求的操作有添加数字、查找后继、删除数字。就可以用平衡树来维护所有新鲜程度大于当前奶牛的牧草。
最后,答案比较大,别忘了开 long long。
code:
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
using namespace std;
const int M=1e5+10;
const int inf=0x3f3f3f3f;
struct node{
int prize,fresh;
}a[M],b[M];
bool cmp(node a,node b)
{
return a.fresh>b.fresh;
}
struct treap{
int cnt,son[2],val,f;
}tr[M];
long long ans,ans1;
int tot,root;
int newnode(int x)
{
tr[++tot].val=x;
tr[tot].cnt=1;
tr[tot].f=rand();
return tot;
}
void build_tree()
{
newnode(-inf),newnode(inf);
root=1;
tr[1].son[1]=2;
}
void rotate(int &p,int d)
{
int k=tr[p].son[d^1];
tr[p].son[d^1]=tr[k].son[d];
tr[k].son[d]=p;
p=k;
}
void insert(int &p,int x)
{
if(p==0) p=newnode(x);
else if(tr[p].val==x) tr[p].cnt++;
else if(tr[p].val<x)
{
insert(tr[p].son[1],x);
if(tr[tr[p].son[1]].f<tr[p].f) rotate(p,0);
}
else
{
insert(tr[p].son[0],x);
if(tr[tr[p].son[0]].f<tr[p].f) rotate(p,1);
}
}
void get_nex(int p,int x)
{
if(!p) return ;
if(tr[p].val>=x)
{
ans1=tr[p].val;
get_nex(tr[p].son[0],x);
}
else get_nex(tr[p].son[1],x);
}
void delete_val(int &p,int x)
{
if(tr[p].val==x)
{
if(tr[p].cnt>1) tr[p].cnt--;
else
{
if(tr[p].son[0]*tr[p].son[1]==0) p=tr[p].son[1]+tr[p].son[0];
else if(tr[tr[p].son[0]].f<tr[tr[p].son[1]].f) rotate(p,1),delete_val(tr[p].son[1],x);
else rotate(p,0),delete_val(tr[p].son[0],x);
}
}
else if(tr[p].val<x) delete_val(tr[p].son[1],x);
else delete_val(tr[p].son[0],x);
}
int main()
{
build_tree();
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d%d",&a[i].prize,&a[i].fresh);
for(int i=1;i<=m;i++) scanf("%d%d",&b[i].prize,&b[i].fresh);
sort(a+1,a+n+1,cmp);
sort(b+1,b+m+1,cmp);
int now=1;
for(int i=1;i<=n;i++)
{
while(b[now].fresh>=a[i].fresh&&now<=m) insert(root,b[now++].prize);
ans1=-1;
get_nex(root,a[i].prize);
if(ans1==-1)
{
printf("-1\n");
return 0;
}
ans+=ans1;
delete_val(root,ans1);
}
printf("%lld\n",ans);
return 0;
}
应用 [HNOI2002]营业额统计
题意
在 \(n\) 天内,每天都有一个营业额,第 \(i\) 天的最小波动值定义为 \(\min|s_i-s_j|(1 \leq j < i)\)。求 \(n\) 天内的最小波动值之和。
思路
对于第 \(i\) 天的最小波动值。可以求出 \(s_i\) 的前驱 \(s_1\) 和后继 \(s_j\),那么第 \(i\) 天的最小波动值就为 \(\min(s_i-s_1,s_2-s_i)\)。
于是就可以用平衡树来求解。
code:
#include<cstdio>
#include<cstdlib>
#include<ctime>
using namespace std;
const int N=5e4+10;
const int INF=0x3f3f3f3f;
struct NODE{
int l,r,val,cnt,f;
}node[N];
int tot,root=1;
int max(int a,int b){return a<b?b:a;}
int min(int a,int b){return a>b?b:a;}
int newnode(int x)
{
node[++tot].val=x;
node[tot].f=rand();
node[tot].cnt=1;
return tot;
}
void zag(int &p)
{
int k=node[p].l;
node[p].l=node[k].r,node[k].r=p,p=k;
}
void zig(int &p)
{
int k=node[p].r;
node[p].r=node[k].l,node[k].l=p,p=k;
}
void insert(int &p,int x)
{
if(!p) p=newnode(x);
else if(x==node[p].val) node[p].cnt++;
else if(x<node[p].val)
{
insert(node[p].l,x);
if(node[p].f>node[node[p].l].f) zag(p);
}
else
{
insert(node[p].r,x);
if(node[p].f>node[node[p].r].f) zig(p);
}
}
int get_pre(int x)
{
int ans=-INF,p=root;
while(p)
{
if(node[p].val<=x) ans=max(ans,node[p].val),p=node[p].r;
else p=node[p].l;
}
return ans;
}
int get_nex(int x)
{
int ans=INF,p=root;
while(p)
{
if(node[p].val>=x) ans=min(ans,node[p].val),p=node[p].l;
else p=node[p].r;
}
return ans;
}
int main()
{
srand((unsigned int)time(0));
int n,x;
scanf("%d",&n);
scanf("%d",&x);
newnode(x);
int ans=x;
for(int i=2;i<=n;i++)
{
scanf("%d",&x);
int minn=get_pre(x),maxx=get_nex(x),xx;
xx=min(x-minn,maxx-x);
ans+=xx;
insert(root,x);
}
printf("%d\n",ans);
return 0;
}
应用 [USACO08OPEN]Cow Neighborhoods G
题意
给定 \(n\) 只奶牛,每只奶牛都有一个独一无二的坐标 \((x_i,y_i)\)。当满足下列条件之一时,两只奶牛属于同一个群:
1.两只奶牛的曼哈顿距离不超过 \(C\),即 \(|x_i-x_j|+|y_i-y_j|\leq C\)。
2.两只奶牛有一个共同的邻居,即存在一头奶牛 \(k\),使得 \(i\) 和 \(k\),\(k\) 和 \(j\) 均属于同一群。
求一共有多少个群,以及最大的群里有多少奶牛。
思路
注意到题目中的第二个条件。可以发现,在一个群中,每头奶牛只需存在一头奶牛与它的曼哈顿距离不超过 \(C\) 即可,而不是所有奶牛之间的距离都不超过 \(C\)。也就是本题中的群具有传递性。于是就可以用并查集来标记每个点属于哪个群。
对于题目中的曼哈顿距离,因为有两个绝对值符号的存在,所以直接求解有些困难。于是就可以用到曼哈顿距离转化成切比雪夫距离的技巧,即将原坐标 \((x,y)\) 转化为 \((x+y,x-y)\),在新坐标系中的切比雪夫距离就是原坐标的曼哈顿距离。(具体证明可以看一下这篇博客)
切比雪夫距离的定义为 \(\max(|x_i-x_j|,|y_i-y_j|)\),此时虽然只是将求和改成了取最大值,但是省去了不少麻烦。
在新坐标系中,对于一个点 \((x_i,y_i)\),就可以在所有满足 \(|x_i-x_j| \leq C\) 的坐标中,找到与其 \(y_i\) 相差最小的 \(y_j\),即 \(y_i\) 的前驱和后继,那么如果满足 \(|y_i-y_j| \leq C\) ,就可以将这两个点放到同一个群中。下面简单证明一下该做法的正确性:
当 \(|y_i-y_j| > C\) 时,与 \(y_i\) 值相差最小的点都不满足要求,其他点就更不可能满足了。
当 \(|y_i-y_{k}| \leq C\) 时(\(k\) 点为 \(j\) 点的前驱),也就是对于第 \(i\) 个点,除了前驱和后继,还有其他点满足要求(这里举的是前驱的例子,绝对值符号其实可以拿走,后继的证明同理)。显然 \(|y_j-y_{k}| \leq C\) 也是成立的,那么在此前就已经把 \(j\) 和 \(k\) 这两个点合并了,此时只要把第 \(j\) 个点和第 \(i\) 个点合并,\(i\) 和 \(k\) 就在同一个群中了。
当 \(|y_i-y_{k}| > C\) 时。根据本题中群的传递性,只要满足 \(|y_i-y_j| \leq C,|y_j-y_k| \leq C\),那么 \(i\) 点和 \(j\) 点也就属于同一个群。如果不满足第一个不等式,那么 \(i\) 和 \(j\) 就不会合并;如果不满足第二个不等式,那么 \(j\) 就不会和 \(k\) 合并。那么 \(i\) 和 \(j\) 就不会在一个群中了。
对于快速求出所有满足 \(|x_i-x_j| \leq C\) 的点。就可以先将所有点按 \(x_i\) 的大小排序,然后每一次插入时把最小的不满足要求的点删去即可(有点类似于单调队列的思想)。
对于求 \(y_i\) 的前缀和后继,可以用 set 平衡树来维护。
最终的时间复杂度就为 \(O(n \log n)\)。
还有一些细节见代码。
code:
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<ctime>
using namespace std;
const int N=1e5+10;
const int INF=2e9+10;//题目中的点最大为2e9
struct tree{
int son[2],val,cnt,f,id;//题目中可能会出现y的值相同的点
}tr[N];
struct bot{
int x,y,id;
bool operator <(const bot &t)const{
return x<t.x;
}
}a[N];
int n,c,fa[N],siz[N],num,root;
int ans1,ans2;
int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);} //路径压缩
void merge(int x,int y)
{
int fx=find(x),fy=find(y);
if(fx==fy) return;
ans1--;
if(siz[fx]>siz[fy]) fa[fy]=fx,siz[fx]+=siz[fy];//按秩合并
else fa[fx]=fy,siz[fy]+=siz[fx];
}
int newnode(int val,int id) //Treap 的基本操作
{
tr[++num].cnt=1;
tr[num].val=val;
tr[num].id=id;
tr[num].f=rand();
return num;
}
void rotate(int &p,int d)
{
int q=tr[p].son[d^1];
tr[p].son[d^1]=tr[q].son[d],tr[q].son[d]=p;
p=q;
}
void insert(int &p,int val,int id)
{
if(!p)
{
p=newnode(val,id);
return ;
}
if(val<tr[p].val) //本题要求将相同的点也用不同的编号记录
{
insert(tr[p].son[0],val,id);
if(tr[p].f<tr[tr[p].son[0]].f) rotate(p,1);
}
else
{
insert(tr[p].son[1],val,id);
if(tr[p].f<tr[tr[p].son[1]].f) rotate(p,0);
}
}
void build_tree()
{
newnode(-INF,0),newnode(INF,0);
root=1;
tr[1].son[1]=2;
if(tr[1].f<tr[2].f) rotate(root,0);
insert(root,a[1].y,a[1].id);//第一个点可以特判一下,因为y可能会相同
}
void remove(int &p,int val)
{
if(val==tr[p].val)
{
if(tr[p].son[0]+tr[p].son[1]==0) p=0;
else if(tr[p].son[0]*tr[p].son[1]==0) p=tr[p].son[0]+tr[p].son[1];
else
{
if(tr[tr[p].son[0]].f>=tr[tr[p].son[1]].f) rotate(p,1),remove(tr[p].son[1],val);
else rotate(p,0),remove(tr[p].son[0],val);
}
return ;
}
if(tr[p].val<val) remove(tr[p].son[1],val);
else if(tr[p].val>val) remove(tr[p].son[0],val);
}
int get_pre(int p,int val)//这里返回的是节点编号而不是具体的值,因为还要用到该点的编号
{
if(!p) return 0;
if(tr[p].val>val) return get_pre(tr[p].son[0],val);
int k=get_pre(tr[p].son[1],val);
if(!k) return p;//如果没有右子树,就返回自身
return k;// k是在右子树中的最大值,那么显然当k存在时,tr[k].val才是val的前驱
}
int get_nex(int p,int val)
{
if(!p) return 0;
if(tr[p].val<val) return get_nex(tr[p].son[1],val);
int k=get_nex(tr[p].son[0],val);
if(!k) return p;
return k;
}
int main()
{
srand((unsigned int)time(0));
//freopen("233.in","r",stdin);
scanf("%d%d",&n,&c);
for(int x,y,i=1;i<=n;i++)
{
scanf("%d%d",&x,&y);
a[i].x=(x+y),a[i].y=(x-y),a[i].id=i;//坐标转换,当前节点的编号在合并时会用到
fa[i]=i,siz[i]=1;
}
sort(a+1,a+n+1);
build_tree();
int pos=1;
ans1=n;
for(int i=2;i<=n;i++)
{
while(a[i].x-a[pos].x>c) remove(root,a[pos++].y);//删去不符合要求的点
int pre=get_pre(root,a[i].y),nex=get_nex(root,a[i].y);
if(a[i].y-tr[pre].val<=c) merge(a[i].id,tr[pre].id);//这里别忘了判断
if(tr[nex].val-a[i].y<=c) merge(a[i].id,tr[nex].id);//如果不用原来的编号来合并,就会出现错误
ans2=max(ans2,siz[fa[a[i].id]]);//注意 fa[a[i].id] 才是当前点所在的并查集的编号
insert(root,a[i].y,a[i].id);//别忘了加入当前点
}
printf("%d %d\n",ans1,ans2);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号