UVA11354 Bond 【并查集按秩合并】

题意

给定一个 \(n\) 个顶点 \(m\) 条边的带权无向图，多次询问在两个点之间所有可能的路径中的最大值，最小为多少。

思路

显然，可以先在用 kruskal 算法在原图上构造一棵最小生成树。可以证明，两点之间的路径在这棵树上时，边权的最大值最小。

而对于找到这个最大值有两种做法，一种是在求最近公共祖先时记录下路径上的最大值；另一种作法是在构造生成树时的并查集使用按秩合并优化，直接在并查集（注意不是在生成树上）上求边权的最大值。这里主要介绍后一种作法。

并查集的按秩合并优化

所谓的秩，有两种定义方法。一种是表示树的深度（未路径压缩时），另一种是表示集合的大小。这里可以定义为树的大小。按秩合并就是把秩小的并查集合并为秩较大的并查集的儿子。最终得到的并查集会有树形结构。同时为了维护这个树形结构，就不能再使用路径压缩优化了。

而使用按秩合并后的并查集，每次查询操作的均摊复杂度是 \(O(logn)\)。可以接受。

可以发现，在 kruskal 算法中使用按秩合并优化时，如果在合并时记录一下边权，最终得到的并查集会有一个很有意思的性质：在一条链上，深度越低的边，边权越大。

这是因为在构造最小生成树的时候，如果一直是最初合并的子树秩最大，那么就会一直把新的那一条边添加到这棵树中，此时最终得到的并查集深度也就只有一层了。同时由于边权从小到大的性质，任意两个点之间的路径中边权最大值也一定在这两个点到根节点的边权其中之一。

而对于更一般的情况，如下图中的的带权无向图。

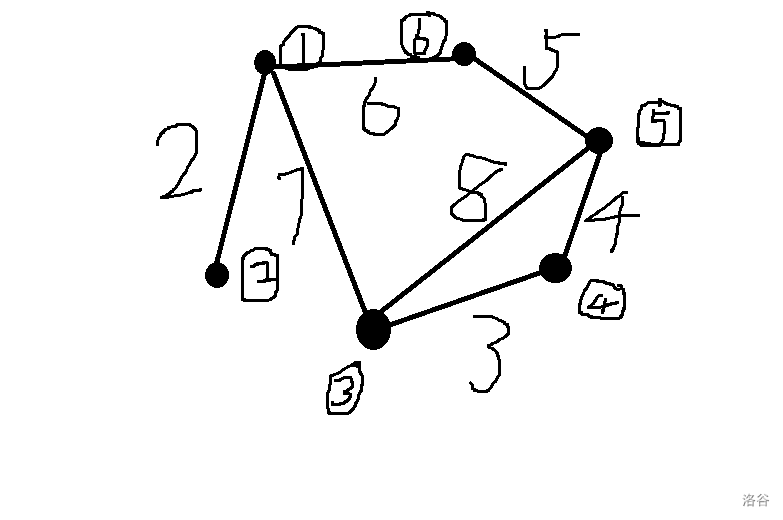
按照 kruskal 算法的流程，最终得到的带权并查集（非生成树）如下图所示：

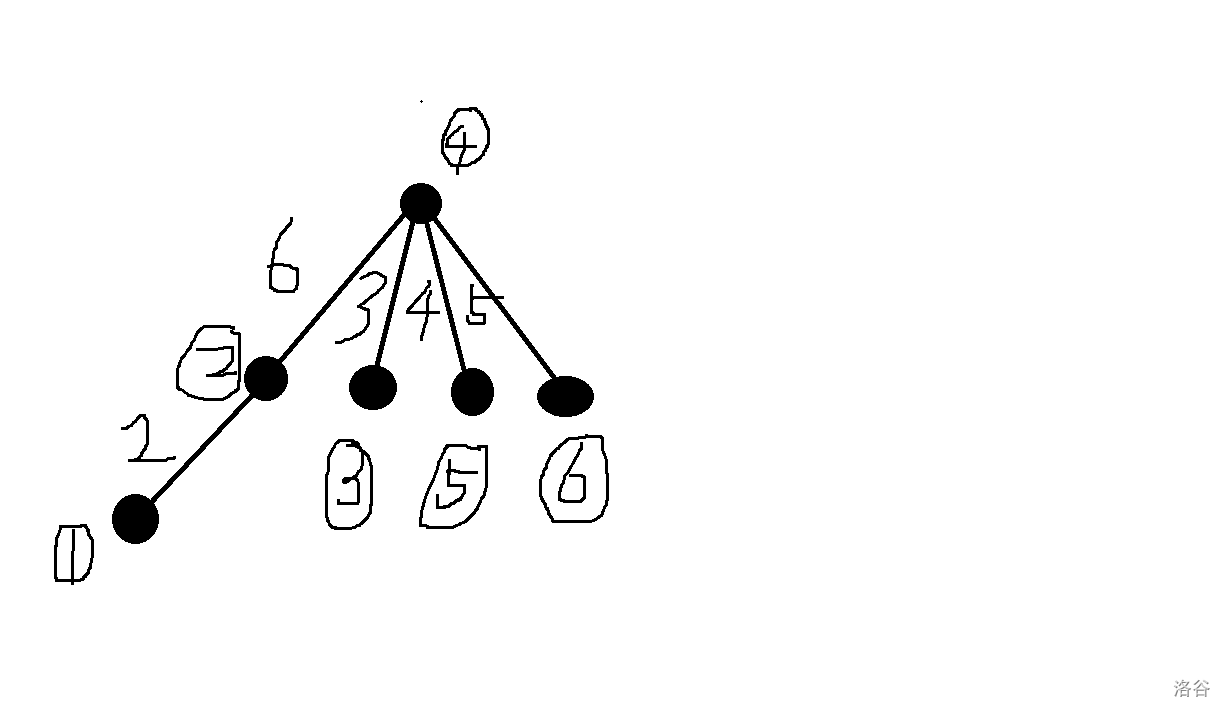
最终得到的并查集也满足这个特殊性质。

设当前边连接一棵子树 \(A\) 和一棵子树 \(B\)。由于最初依据边权大小对边进行了排序，所以这条边的边权一定比之前的任何一条边都要大。

当 \(A\) 的秩比 \(B\) 小时，就会将 \(A\) 的树根连接到 \(B\) 的树根上，而这条边的边权就是这条最大的边权， 所以 \(A\) 向 \(B\) 连的这条边肯定比 \(A\) 中的任何一条边的边权都要大。

当 \(A\) 的秩比 \(B\) 大时，同样也满足新的这条边比 \(B\) 中任意一条边的边权都大，也就满足了最初提到的性质。（这里只是简单的证明了一下，并未严格证明）

因为我们只关心路径上最大边权的最小值，并不关心这条路径怎么走。故虽然在按秩合并时破坏了两点之间路径的顺序，但是在最小生成树中已经保证了两点之间必定联通，所以并不会对答案产生影响。

于是可以根据以上的性质。对于 \(x,y\) 两点，先以 \(x\) 为起点向上走，同时记录路径上经过的每一个点之前的边权（后面会提到用处）。以及边权的最大值，由于上面提到的性质，最大值直接更新就好了，不需要比较。

再以 \(y\) 为起点向上走，同样也记录边权的最大值，如果遇到了某一个节点，该节点经过之前的边权已经被赋值了，那么就说明有两种情况。要么就是 \(x\) 和 \(y\) 在同一条链上，但是不知道谁的深度更大，如果 \(y\) 在 \(x\) 的下面，那么搜到的这个节点就是 \(x\) 本身了，但是这个节点向下的边权是没有记录的，所以答案需要取当前这个点向下的最大值和路径上的最大值较大的那个；要么就是已经搜到了根节点，在此时需要取从 \(x\) 往上走的最大值和从 \(y\) 往上走的最大值较大的那个。所以此处的取 \(max\) 是不可省略的。

最终还要注意一下题目中要求的输出格式，就可以通过本题了。

code：

#include<cstdio>
#include<algorithm>
using namespace std;
const int N=5e4+10;
const int M=1e5+10;
int f[N],cnt[N],n,m,vis[N],val[N],q;
struct edge{
	int u,v,w;
	bool operator <(const edge &t)const{
	    return w<t.w;
	}
}e[M];
int find(int x){return f[x]==x?x:find(f[x]);}
void kruskal()
{
	for(int i=0;i<=n;i++) f[i]=i,cnt[i]=1,val[i]=0;
	sort(e+1,e+m+1);
	for(int i=1;i<=m;i++)
	{
		int u=e[i].u,v=e[i].v,w=e[i].w;
		int fx=find(u),fy=find(v);
		if(fx==fy) continue;
		if(cnt[fx]>cnt[fy]) f[fy]=fx,cnt[fx]+=cnt[fy],val[fy]=w;
		else f[fx]=fy,cnt[fy]+=cnt[fx],val[fx]=w;
	}
}
int NLC(int x,int y)
{
	for(int i=0;i<=n;i++) vis[i]=0;
	int ans1=1,ans2=0,now=x;
	bool NLCAKIOI=false;
	while(!NLCAKIOI)
	{
		vis[now]=ans1;
		if(now==f[now]) break;
		ans1=val[now];
		now=f[now];
	}
	now=y;
	while(!NLCAKIOI)
	{
		if(vis[now])
		{
			ans2=max(ans2,vis[now]);
			break;
		}
		if(now==f[now]) break;
		ans2=val[now];
		now=f[now];
	}
	return ans2;
}
int main()
{
	int T=0;
	while(scanf("%d%d",&n,&m)!=EOF)
	{
		if(T) puts("");
		else T++;
		for(int i=1;i<=m;i++) scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w);
		kruskal();
		scanf("%d",&q);
		while(q--)
		{
			int x,y;
			scanf("%d%d",&x,&y);
			printf("%d\n",NLC(x,y));
		}
	}
	return 0;
}