树形DP总结
树形动态规划,即在树上进行的动态规划。
因为树的递归性质,树形动态规划一般都是递归求解的。(摘自洛谷题单)
没有上司的舞会(经典树形DP入门题)
题意
公司的每一个职员都有从属关系(除校长外),所有职员的从属关系构成一棵树,每一个职员都不会和他的直接上司同时参加舞会。每一位职员都有一个快乐指数,求一种参会方案使得参加舞会的人的快乐指数最大,并输出最大的快乐指数。
思路
通过题意可以发现,对于每个职员\(x\)有两种状态,去和不去,于是可以考虑用\(f[x][0]\)和\(f[x][1]\)分别表示以\(x\)为根的子树中,职员\(x\)去与职员\(x\)不去这种状态下最多的参会人数。设校长的编号为\(root\),最终的答案即为\(max(f[root][0]\),\(f[root][1])\)。
考虑转移
首先可以发现x的任意两个子节点直接并没有依赖关系,所以x的状态可以用x的所有子节点的状态累加得出。
当x参加舞会时,那么x的直接下司y只能不参加,即\(f[x][1]+=f[y][0]\)
而x不参加舞会,那么x的直接下司y就有参加与不参加两种状态,即\(f[x][0]+=max(f[y][0],f[v][1])\)
code:
#include<bits/stdc++.h>
using namespace std;
const int M=6e3+10;
int h[M],v[M],f[M][2],n;
vector<int> son[M];
void dp(int u)
{
f[u][0]=0;
f[u][1]=h[u];
for(int i=0;i<son[u].size();i++)
{
int j=son[u][i];
dp(j);
f[u][0]+=max(f[j][0],f[j][1]);
f[u][1]+=f[j][0];
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>h[i];
for(int x,y,i=1;i<n;i++)
{
cin>>x>>y;
son[y].push_back(x);
v[x]=1;
}
int root;
for(int i=1;i<=n;i++)
{
if(v[i]==0)
{
root=i;
break;
}
}
dp(root);
cout<<max(f[root][0],f[root][1])<<endl;
}
[CTSC1997]选课(有依赖的背包问题)
本题还有一题弱化版二叉苹果树,因为思路大体一致,就略过了。
题意
给定一棵树,每个节点都有一个权值,若选\(v\)这个节点,就必须先选\(v\)的父亲\(u\)。现在要选出\(m\)个点,求最大的权值之和。
思路
设\(f[i][j]\)表示在以\(i\)为根的字数内选择\(j\)个节点所能得到的最大值。
初始化:\(f[i][1]=val[i]\),因为选一个只能选根节点。
对于\(u\)的子节点\(v_i\),先递归处理出\(f[v_i]\),那么就可以得到状态转移方程:\(f[u][j]=max(f[u][k]+f[v_i][j-k])\),也就是说从\(u\)的其他分支上选\(k\)个节点,再从\(v_i\)这条分支上选\(j-k\)个节点。
细节
本题中有一些节点的父节点为\(0\),虽然题目描述中说是无父节点,但是可以将\(0\)号节点当成超级源点。故要多选一个\(0\)号节点,所以最多选的节点数为\(m+1\),最终的答案就是\(f[0][m+1]\)。
code:
#include<bits/stdc++.h>
using namespace std;
const int M=310;
int f[M][M],n,m;
vector<int> v[M];
void dfs(int u)
{
for(int i=0;i<v[u].size();i++)
{
int to=v[u][i];
dfs(to);
for(int j=m+1;j>=1;j--)
for(int k=0;k<j;k++)
f[u][j]=max(f[u][j],f[to][k]+f[u][j-k]);
}
}
int main()
{
cin>>n>>m;
for(int x,i=1;i<=n;i++)
{
cin>>x>>f[i][1];
v[x].push_back(i);
}
dfs(0);
cout<<f[0][m+1]<<endl;
return 0;
}
皇宫看守(状态设计)
题意
给定一棵树,每个节点都有一个权值,选择一个节点的同时也选择了与该节点相邻的所有节点。求用最小的权值之和覆盖所有的点。
思路
本题与没有上司的舞会有点相似,但是如果照搬状态,\(0\) 表示不选这个节点,\(1\) 表示选这个节点。会发现一个奇怪的问题:如何转移状态方程?\(f[i][0]=?\),可以发现,如果 \(i\) 这个节点不选,那么 \(i\) 的子节点 \(j\) 选与不选是不确定的,因为可以选择 \(i\) 的父节点,\(j\) 的子节点,这样子也可以覆盖这两个节点。但是,也可以选择\(j\),不选\(j\) 的子节点。但是这样做又无法保证所有的节点都被选择。于是需要用新的状态设计。
\(f[i][0]\) 表示 \(i\) 被它的父节点看到。\(f[i][0]+=min(f[j][2],f[j][1]),j\) 为 \(i\) 的子节点
\(f[i][1]\) 表示 \(i\) 被它的子节点看到。情况较为复杂,单独考虑。
\(f[i][2]\) 表示 选择 \(i\) 本身。 \(f[i][2]=min(f[j][0],f[j][1],f[j][2])\)
对于 \(f[i][1]\) ,由于直接转移无法保证 \(i\) 的所有子节点都被覆盖。所以要先用 \(sum\) 统计出覆盖 \(i\) 的所有子节点所用的最小权值和,即 \(sum+=min(f[j][1],f[j][2])\)。然后枚举\(i\)被哪个子节点看到,先减去在 \(sum\) 的条件下需要的权值,再加上 \(f[j][2]\) ,这样就可以保证 \(i\) 的所有子节点都被看到。
\(f[i][1]=min(sum-min(f[j][1],f[j][2])+f[j][2])\) 。
最终的答案就是 \(min(f[root][0],f[root][1])\)。因为根节点无法被它的父节点看到。\(root\) 在本题中并未说明是 \(1\) 号节点。故需在输入的时候找出根节点。
code:
#include<cstdio>
using namespace std;
const int N=1520;
const int INF=0x3f3f3f3f;
int f[N][3],val[N],h[N],idx,n;
struct edge{
int v,nex;
}e[N*N];
bool st[N];
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
void add(int u,int v)
{
e[++idx].v=v;
e[idx].nex=h[u];
h[u]=idx;
}
void dp(int u)
{
f[u][2]=val[u];
int sum=0;
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
dp(v);
f[u][0]+=min(f[v][1],f[v][2]);
f[u][2]+=min(min(f[v][0],f[v][1]),f[v][2]);
sum+=min(f[v][1],f[v][2]);
}
f[u][1]=INF;
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
f[u][1]=min(f[u][1],sum-min(f[v][1],f[v][2])+f[v][2]);
}
}
int main()
{
scanf("%d",&n);
for(int id,w,m,v,i=1;i<=n;i++)
{
scanf("%d%d%d",&id,&w,&m);
val[id]=w;
for(int j=1;j<=m;j++) scanf("%d",&v),add(id,v),st[v]=true;
}
int root=1;
while(st[root]) root++;
dp(root);
printf("%d\n",min(f[root][1],f[root][2]));
}
SP1437 PT07Z - Longest path in a tree(树的直径)
本题为树的直径模板题。
题意
给定一棵树,求出树中最远的两个节点之间的距离(树的直径)。
思路
树的直径一般有两种做法,树形 DP 和两次 BFS。时间复杂度都为\(O(n^2)\)。这里介绍树形 DP 的做法。
设 \(1\) 号节点为根节点。
设 \(d[u]\) 表示以\(u\)为根节点向下能到达的最远距离。\(v_i\) 为 \(u\) 的儿子,那么,\(d[u]=max(d[v_i]+w[i])\)。
设经过 \(u\) 的最长链的长度为 \(f[u]\) 。设 \(v_i\) 和 \(v_j\) 为 \(u\) 的两个不同儿子。显然,\(f[u]=max(d[v_i]+w[i]+d[v_j]+w[j])\)。但是如果直接枚举 \(u\) 的儿子,时间复杂度就会到达 \(O(n^2)\) 级别,显然无法通过本题。
考虑优化,不妨设 \(i<j\),那么对于确定的 \(j\),\(d[v_j]+w[j]\) 就是一个确定的常数。同时可以惊奇的发现,\(max(d[v_i]+w[i])\) 就是在遍历 \(v_j\) 之前的 $ d[u]\(。发现这个结论以后,就可以做到\)O(n)$时间内解决这道题。
最终的答案就是 \(max(f[u])\)。
code:
#include<cstdio>
using namespace std;
const int N=1e4+10;
const int M=2e4+10;
int d[N],f[N],n,idx,h[N],ans;
struct edge{
int v,w,nex;
}e[M];
int max(int a,int b){return a>b?a:b;}
void add(int u,int v,int w)
{
e[++idx].v=v;
e[idx].w=w;
e[idx].nex=h[u];
h[u]=idx;
}
void dp(int u,int fa)
{
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(v==fa) continue;
dp(v,u);
ans=max(ans,d[u]+e[i].w+d[v]);
d[u]=max(d[u],e[i].w+d[v]);
}
}
int main()
{
scanf("%d",&n);
for(int u,v,i=1;i<n;i++)
{
scanf("%d%d",&u,&v);
add(u,v,1),add(v,u,1);//本题默认一条边的长度为1
}
dp(1,-1);
printf("%d\n",ans);
return 0;
}
数字转换(建模+树的直径)
题意
如果一个数\(x\)的约数之和\(y\)(不包括他本身)比他本身小,那么\(x\)可以变成 \(y\),\(y\)也可以变成\(x\)。
限定所有数字变换在不超过\(n\)的正整数范围内进行,求不断进行数字变换且不出现重复数字的最多变换步数。
思路
初看本题,似乎和树型\(DP\)没有任何联系。。但是通过题意可以发现,每一个数的约数之和是确定的,也就是说每一个数和它的约数之和的关系是确定的,当满足约数之和小于这个数本身时,就可以在这两个数之间连一条边,最终就可以得到一棵树。题目要求的是最多变换次数,显然
,这就是树的直径。于是本题就可以转化成树的直径模板题进行求解了。
细节&优化
本题的数据最大有\(50000\),试除法的时间复杂度为\(O(n\sqrt n)\),可以通过本题,但是如果数据规模大一些就会\(TLE\),所以可以采取更高效率的方法。试除法是枚举每一个数的约数,我们也可以用约数来反推每一个数,也就是将\(i\)的\(j\)倍数的约数之和中加入\(i\),注意这里\(j\)要从\(2\)开始枚举,因为题目中说“不包含本身”。这种做法的时间复杂度为\(O(nlogn)\)。
本题的数的大小关系是确定的,故可以只用从\(i\)的约数之和向\(i\)连一条有向边,这样可以省下一半的空间。
最后的枚举从\(1\)开始,因为\(1\)可以连向所有的质数,这些质数又可以与合数相连(具体证明由于本人太菜就略过了)。
#include<cstdio>
using namespace std;
const int N=50010;
struct edge{
int v,nex;
}e[N];
int d[N],sum[N],h[N],idx,n,ans;
int max(int a,int b){return a>b?a:b;}
void add(int u,int v)
{
e[++idx].v=v;
e[idx].nex=h[u];
h[u]=idx;
}
void dp(int u)
{
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
dp(v);
ans=max(ans,d[u]+d[v]+1);
d[u]=max(d[u],d[v]+1);
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
for(int j=2;j<=n/i;j++)
sum[i*j]+=i;
for(int i=2;i<=n;i++)
if(sum[i]<i) add(sum[i],i);
dp(1);
printf("%d\n",ans);
return 0;
}
Accumulation Degree(二次扫描+换根法)
二次扫描+换根法的经典模板题。
题意
给出一张带权图,求以哪个根为节点时的最大流量最大,并输出这个最大值。
思路
朴素的做法,以每个节点为根遍历一遍全图求最大流量,这种做法的时间复杂度为\(O\)(\({n^2}\)),显然无法通过本题。
于是就要用到神奇的换根法来解决这道题。
换根法一般有两个步骤,从下往上递推和从上往下递推。
通俗地讲,就是先用子节点更新父节点,之后再用父节点更新子节点
对于本题来说,可以先考虑以某一节点为根节点(题干中并未指出1号节点为根节点),层层递归,求出每一个节点向下的最大流量。
之后再以原来的根节点为起点遍历一遍,在遍历的时候就可以用父亲节点的信息来更新儿子节点。具体情况如下图所示,
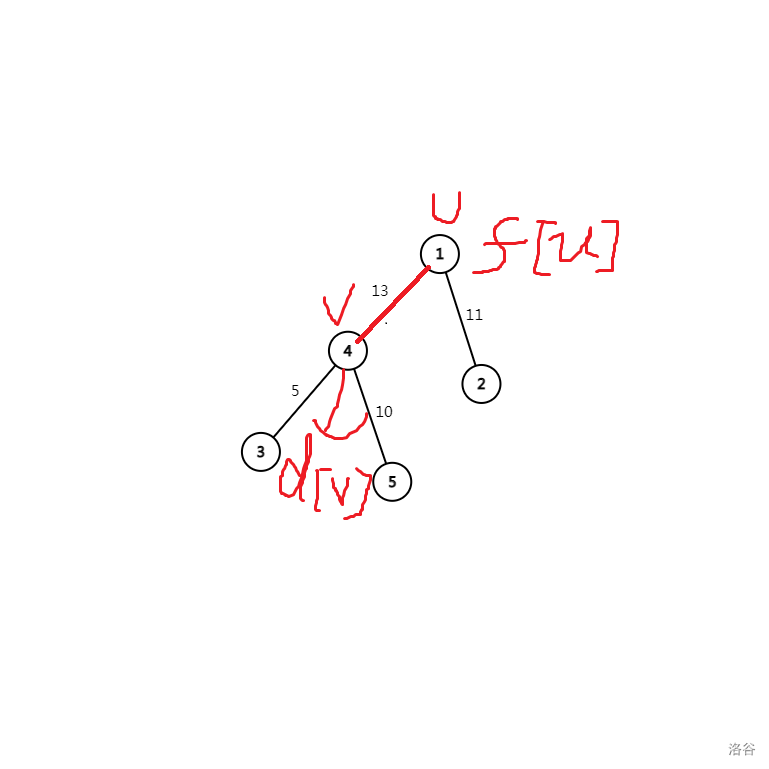
在第二次遍历时,遍历到图中红色边的时候,\(d[v]\)即为\(v\)节点往下的最大流量,在此处即为\(15\),通过第一次遍历以后,已经得出了\(d[1]\),为\(1\)号节点向下的最大流量,在此处也可以表达为以\(1\)号节点为根的最大流量。即\(f[1]\)。
那么现在如何通过\(1\)号节点得出\(f[4]\)呢?
可以发现,\(f[4]\)由\(d[4]\)和\(4\)号节点向上的最大流量,而\(d[4]\)在此前已经求得;通过分析可以发现,\(4\)号节点向上的最大流量是 \(f[u]-\)在红边上的流量与这条红边最大流量的最小值,即 \(f[v]=d[v]+{min(f[u]-min(d[v],w[i]),w[i])}\)。
那么如果v为叶子节点呢?
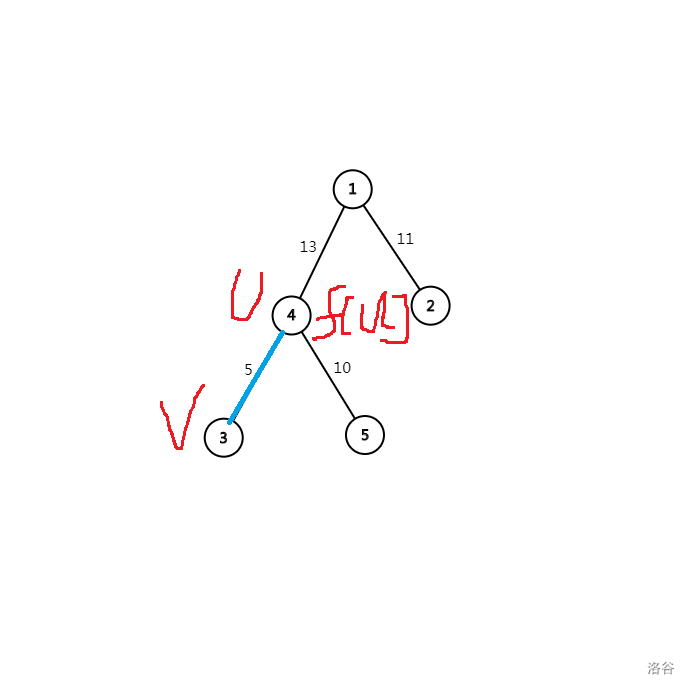
如本图中的蓝色边。通过观察可以发现,\(f[v]\)为\(f[u]-\)以\(u\)为根节点时这条边上的流量与这条边最大流量的最小值,而由于\(u\)节点往\(v\)方向流,除了\(w[i]\)以外无任何限制,故\(u\)在这条边上的流量即为\(w[i]\),即 \(f[v]=min(f[u]-w[i],w[i])\)。
细节
由于本题的根节点不一定为\(1\)号点,故要对每一条边的度数进行统计,从前往后遍历,找出第一个度数大于\(1\)个节点,令该点为根节点。但是,良心出题人可能会构造只有一条边的特殊情况,用以上的处理方式就无法得到根节点了。。。此时直接输出\(w[1]\)即可
code:
#include<cstdio>
#include<cstring>
using namespace std;
const int N=2e5+10;
const int INF=0x3f3f3f3f;
int h[N],idx,f[N],d[N],root,n,ans,deg[N];
struct edge{
int v,w,nex;
}e[N<<1];
int min(int a,int b){return a<b?a:b;}
int max(int a,int b){return a>b?a:b;}
void add(int u,int v,int w)
{
e[++idx].v=v;
e[idx].w=w;
e[idx].nex=h[u];
h[u]=idx;
}
int dfs_nlc(int u,int fa)
{
if(deg[u]==1)
{
d[u]=INF;
return INF;
}
d[u]=0;
for(int i=h[u];~i;i=e[i].nex)
{
int v=e[i].v;
if(v==fa) continue;
d[u]+=min(e[i].w,dfs_nlc(v,u));
}
return d[u];
}
void init()
{
root=1;
idx=ans=0;
memset(h,-1,sizeof(h));
memset(f,0,sizeof(f));
memset(d,0,sizeof(d));
memset(deg,0,sizeof(deg));
}
void dfs_yy(int u,int fa)
{
for(int i=h[u];~i;i=e[i].nex)
{
int v=e[i].v;
if(v==fa) continue;
if(deg[v]==1) f[v]=min(f[u]-e[i].w,e[i].w);
else
{
f[v]=d[v]+min(e[i].w,f[u]-min(d[v],e[i].w));
dfs_yy(v,u);
}
}
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
init();
for(int u,v,w,i=1;i<n;i++)
{
scanf("%d%d%d",&u,&v,&w);
add(u,v,w),add(v,u,w);
deg[u]++,deg[v]++;
}
while(deg[root]==1&&root<=n) root++;
if(root>n)
{
printf("%d\n",e[1].w);
continue;
}
dfs_nlc(root,-1);
f[root]=d[root];
dfs_yy(root,-1);
for(int i=1;i<=n;i++) ans=max(ans,f[i]);
printf("%d\n",ans);
}
return 0;
}
树的中心(二次扫描+换根法)
二次扫描+换根法的经典模板题\(+1\)。
题意
给定一棵树,求一个点,使得该点到树种其他点的最大距离最小。
思路
第一次扫描:
以任意一个节点为根节点遍历一遍树,求出每个节点\(u\)向下能够到达的最远距离(\(d1[u]\))以及所经过的儿子节点编号(\(p1[u]\))、次远距离(\(d2[u]\))(之后会讲到为什么要求次远距离)。
第二次扫描:
从根节点开始向下遍历,求出每个节点\(u\)向上能够到达的最远距离(\(up[u]\))。

如图所示,对于节点\(v\),\(v\)能够走到的最远距离为\(v\)向下能走的最远距离与\(v\)向上走能走到的最远距离的最大值。
\(v\)向下走的最远距离在第一次遍历时已经求出。而\(v\)向上走的最远距离则为从\(v\)的父节点\(u\)向上走的最远距离与\(u\)不经过\(v\)向下走的最远距离,要分两种情况讨论。
情况一:\(u\)向下走最远距离的这条边经过\(v\),那么\(up[v]=max(up[u],d2[u])+w[i]\)。
情况二:\(u\)向下走最远距离的这条边不经过\(v\),那么\(up[v]=max(up[u],d1[u])+w[i]\)。
细节
对于非叶子节点\(u\),它所能到达的最远距离即为\(max\)(\(up[u]\),\(d1[u]\))。
而对于叶子节点\(v\),它无法向下走,故它所能到的最远距离为\(up[v]\)。
故需要在第一次遍历的同时记录叶子节点。
code:
#include<cstdio>
using namespace std;
const int N=1e4+10;
const int M=2e4+10;
const int INF=0x3f3f3f3f;
struct edge{
int v,w,nex;
}e[M];
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
bool leaf[N];
int up[N],d1[N],d2[N],p1[N],ans=INF,h[N],n,idx;
void add(int u,int v,int w)
{
e[++idx].v=v;
e[idx].w=w;
e[idx].nex=h[u];
h[u]=idx;
}
int dfs_yy(int u,int fa)
{
d1[u]=d2[u]=-INF;
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(v==fa) continue;
int maxd=dfs_yy(v,u)+e[i].w;
if(maxd>=d1[u])
{
d2[u]=d1[u],d1[u]=maxd;
p1[u]=v;
}
else if(maxd>d2[u]) d2[u]=maxd;
}
if(d1[u]==-INF)
{
d1[u]=d2[u]=0;
leaf[u]=true;
}
return d1[u];
}
void dfs_nlc(int u,int fa)
{
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(v==fa) continue;
if(p1[u]==v) up[v]=max(up[u],d2[u])+e[i].w;
else up[v]=max(up[u],d1[u])+e[i].w;
dfs_nlc(v,u);
}
}
int main()
{
scanf("%d",&n);
for(int u,v,w,i=1;i<n;i++)
{
scanf("%d%d%d",&u,&v,&w);
add(u,v,w),add(v,u,w);
}
dfs_yy(1,-1);
dfs_nlc(1,-1);
for(int i=1;i<=n;i++)
{
if(leaf[i]) ans=min(ans,up[i]);
else ans=min(ans,max(d1[i],up[i]));
}
printf("%d\n",ans);
return 0;
}
[ZJOI2006]三色二叉树
计数类题目真良(du)心(liu)。
题意
给定一棵二叉树。对这个二叉树进行染色,可以染红色、绿色、蓝色三种颜色。并且,一个节点与它子节点的颜色不能相同。如果该节点有两个子节点,那么这两个子节点也不能染相同的颜色。求最多和最少有多少个节点可以被染成 ${\color{Green} green} $。
思路
首先这道题给出的二叉树方式很良心。于是首先需要把二叉树的表达式转化为我们所常用的方式。也就是要深搜一遍。对于有两个节点的情况,可以先递归建立左子树,同时记录已经经过的节点数量,递归建立右子数时直接从已经遍历过的节点数量 \(+1\) 开始即可。
然后对于二叉树染色。很容易可以想到与入门题一样的想法,用 \(f[i][0]\) 表示第 \(i\) 个节点不染 ${\color{Green} green} $ 时的最大值,用 \(f[i][1]\) 表示第 \(i\) 个节点染 ${\color{Green} green} $ 时的最大值。(因为最大值和最小值的区别只在于转移方程时取 \(\max\) 和取 \(\min\),所以这里只讨论最大值)
然后对于状态转移方程,就有:
\(f[u][1]=f[tr[u][0]][0]+f[tr[u][1]][0]+1\)。
\(f[u][0]=max(f[tr[u][0]][0]+f[tr[u][1]][0],f[tr[u][0]][0]+f[tr[u][1]][1],f[tr[u][0]][0]+f[tr[u][1]][0])\)。
对于第一个状态转移方程,是否满足了左右子树颜色不同的限制呢?
对于第二个状态转移方程,是否考虑了不存在的染色情况呢?
这时就要用到一个很 NB 的原理——抽屉原理了。
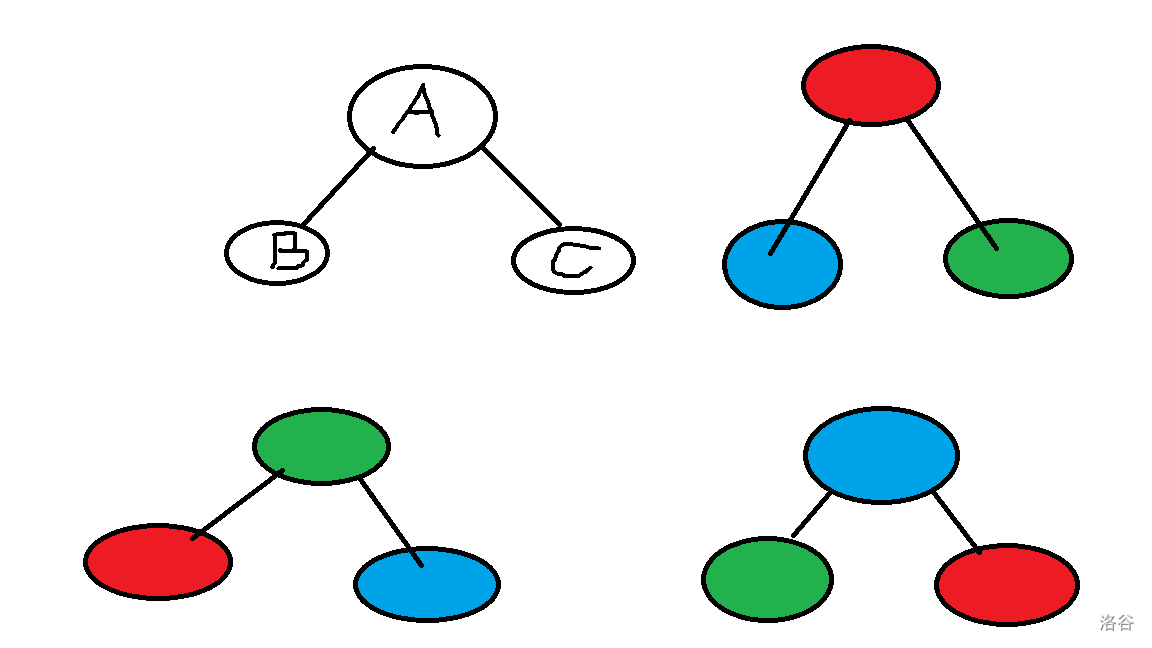
如图所示,这是合法的三种情况,除此之外的其他染色方式,都是不合法的(左右儿子互换就不用提了)。
因为假设 \(A\) 节点染了颜色 \(a\) ,那么 \(B\) 和 \(C\) 就不能染 \(a\) ,同时 \(B\) 和 \(C\) 也要不同色。所以 \(A,B,C\) 三点的颜色一定互不相同。
于是第二个状态转移方程中就不会存在三个节点都不是绿色的情况了,需要山区。
再回头来看第一个状态转移方程。左右两个儿子的颜色其实可以根据需要更改的。
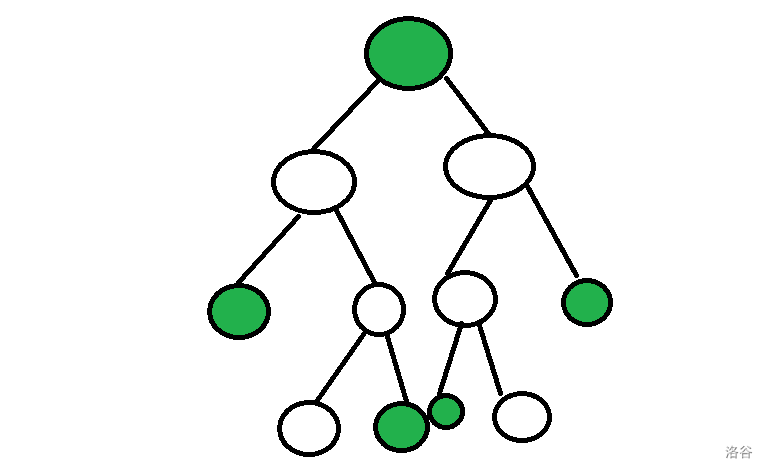
可以发现,对于白色点的颜色,只要满足相邻的颜色(当然不是绿色)不相同,其实就是合法的。
而对于只有一个子节点的情况,显然就更可以“按需分配”了。
最后,别忘了求最小值。
code:
#include<cstdio>
using namespace std;
const int N=5e5+10;
const int INF=0x3f3f3f3f;
int tr[N][2],f1[N][2],tot,f2[N][2];
char s[N];
int min(int a,int b){return a<b?a:b;}
int max(int a,int b){return a>b?a:b;}
void build_tree(int root)
{
tot++;
if(s[root]=='0') return ;
else if(s[root]=='1')
{
tr[root][0]=root+1;
build_tree(root+1);
}
else
{
tr[root][0]=root+1;
build_tree(root+1);
tr[root][1]=tot+1;//root+1在建树前后都可以,但tot+1一定要在建树前
build_tree(tot+1);
}
}
void dfs(int u)
{
for(int i=0;i<2;i++)
{
if(tr[u][i]) dfs(tr[u][i]);
}
f1[u][0]=max(f1[tr[u][1]][1]+f1[tr[u][0]][0],f1[tr[u][1]][0]+f1[tr[u][0]][1]);
f1[u][1]=f1[tr[u][1]][0]+f1[tr[u][0]][0]+1;
f2[u][0]=min(f2[tr[u][1]][1]+f2[tr[u][0]][0],f2[tr[u][1]][0]+f2[tr[u][0]][1]);
f2[u][1]=f2[tr[u][1]][0]+f2[tr[u][0]][0]+1;
}
int main()
{
scanf("%s",s+1);
build_tree(1);
dfs(1);
printf("%d %d\n",max(f1[1][0],f1[1][1]),min(f2[1][0],f2[1][1]));
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号