20172323 2018-2019-1 《程序设计与数据结构》第九周学习总结
20172323 2018-2019-1 《程序设计与数据结构》第九周学习总结
教材学习内容总结
本周学习了第15章图
图和图论衔接了数学和计算机科学的整个分支学科
- 15.1 无向图
- 图由结点和结点间连接而成,这些结点叫做顶点,结点之间的连接叫做边。边(A,B)就意味着从顶点A到顶点B有一条边
- 无向图是一种边为无序结点对的图,也就意味着边(A,B)是A和B之间有一条从两个方向都可以游历的连接。也就是说(B,A)和(A,B)的含义是一样的
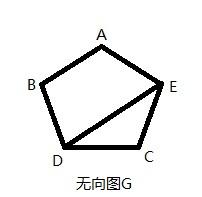
- 如果图中的两个顶点之间有一条连通边,则称这两个顶点是邻接的。如上图,A和B是邻接的,A和C不是邻接的。邻接顶点有时称为邻居,连通一个顶点及其自身的边称为自循环或环。
- 如果无向图拥有最大数目的连通顶点的边,则认为这个无向图是完全的
对有n个顶点的无向图,要使该图是完全的,要求有n(n-1)/2条边
- 路径是图中的一系列边,每条边连通两个顶点。路径的长度是该路中边的条数或者是顶点数减去1.
- 树也是图的一种
- 如果无向图中的任意两个顶点之间都存在一条路径,则认为这个无向图是连通的。
- 环路是一种首顶点和末顶点相同且没有重边的路径。无向树是一种连通的无环无向图,其中一个元素被指定为树根。
- 15.2 有向图
- 有向图也被称为双向图,它是一种边为有序顶点对的图
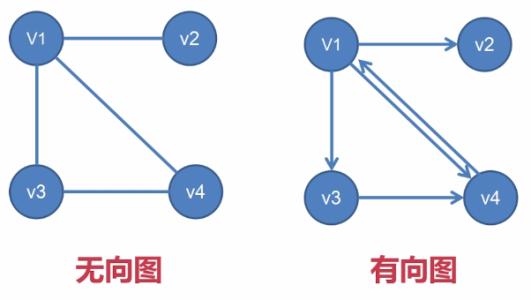
- 有向图中的路径是图中连通两个顶点的有向序列。
- 如果有向图中没有环路,且有一条从A到B的边,则可以把顶点A安排在顶点B之前,这样排列得到的顶点次序称为拓扑序。
- 有向树是一种指定了一个元素做为树根的有向图,该图含有以下性质
- 不存在其他顶点到树根的连接
- 每个非树根元素恰好有一个连接
- 树根到每个其他顶点都有一条路径
- 15.3 网络
- 网络,或称为加权图,是一种每条边都带有权重或代价的图。加权图中的路径权重是该路径中各条边权重的和
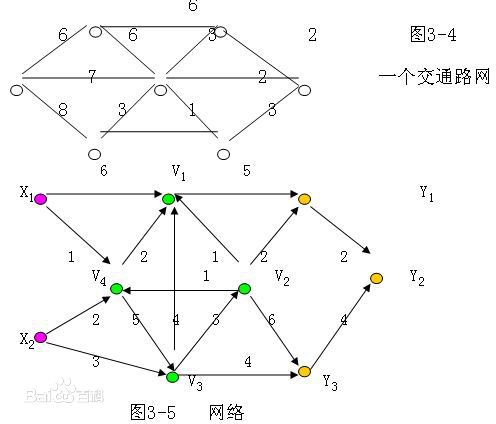
- 根据需要,网络可以是无向的,也可以是有向的。对于网络,我们将用一个三元组来表示每条边,其中包括其实顶点、终止顶点和权重
- 15.4 常用的图算法
- 遍历:图的遍历分为两类,广度优先遍历和深度优先遍历。图中不存在根结点,因此图的遍历可以从其中的任一顶点开始。
- 图的深度优先遍历与广度优先遍历的唯一不同是,它使用的是栈而不是队列来管理遍历
- 测试连通性:不论哪个为起始顶点,当且仅当广度优先遍历中的顶点数目等于图中的顶点数目时,该图才是连通的。
- 最小生成树:生成树是一棵含有图中所有顶点和部分边的树。最小生成树是这样一棵生成树,其边的权重总和小于或等于同一个图中其他任何一棵生成树的权重总和。
- 判定最短路径:一种是判定起始顶点与目标顶点之间的最小边数。一种是寻找加权图的最便宜路径
- 15.5 图的实现策略
- 邻接列表:邻接列表运用到的是二维数组,这个二维数组中的每个单元都表示了两个顶点的交接情况,由布尔值来表示。无向图的邻接矩阵是对称的。
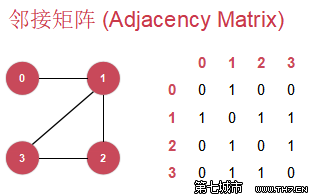
- 15.6 用邻接矩阵实现无向图
教材学习中的问题和解决过程
- 问题1:无向图的广度优先遍历中,第一个顶点有三个邻接顶点,那么下一次遍历的时候必须从最右一个顶点开始遍历吗?
- 问题1解决方案:类似于树的遍历,在同一层中,元素的遍历都是从左到右的进行遍历,图中看似是从右边一个元素开始的,但是第一个遍历的顶点按照树的结构画出来,依旧是从左至右开始遍历。如图是一个图的遍历的顺序
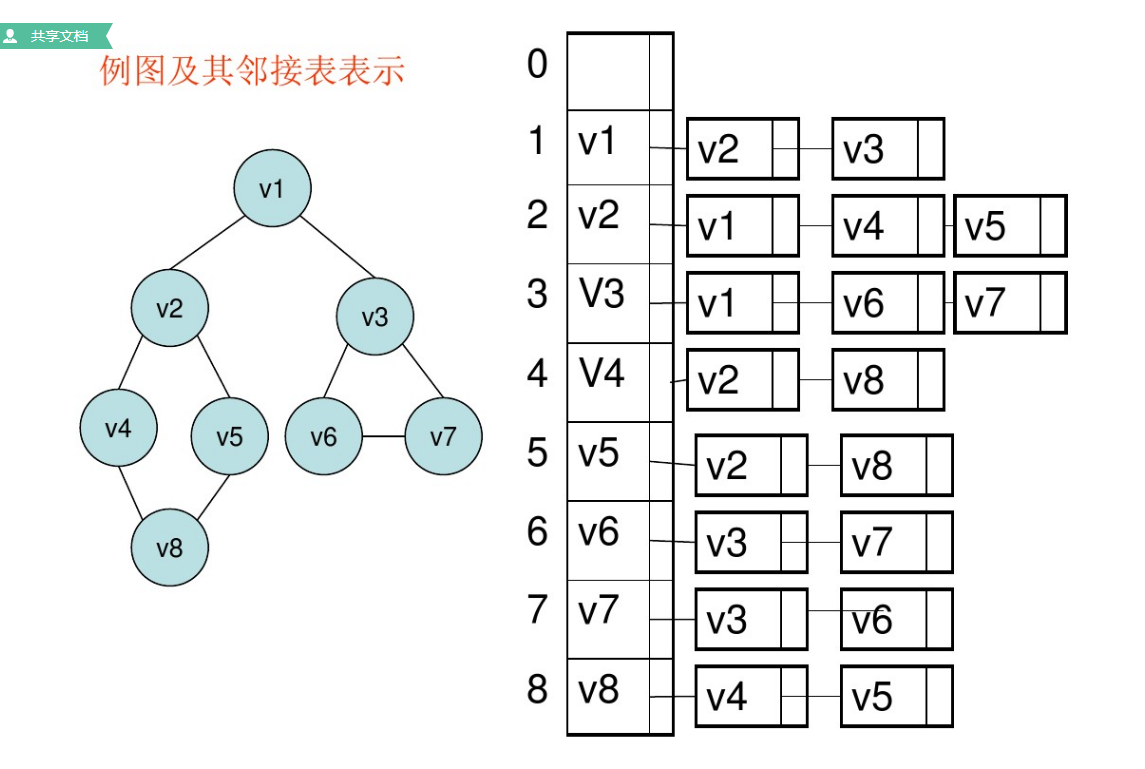
可以看到,每一层都是从左至右地遍历的。如果是已经查看过(visited)的,那么就可以跳过查看它的下一个
- 问题2:addEdge方法里运用到的几个方法getIndex、indexIsValid分别是什么意思
- 问题2解决方案:因为无向图的实现是由一个顶点列表和邻接矩阵组合而成的,所以如果要在两个顶点之间添加一条边,首先需要在顶点列表中找到这两个顶点,getIndex就是这样一个方法,用于定位正确的索引。indexIsValid则是用于判断索引值是否合法,如果合法的话就把邻接矩阵内两个顶点之间对应的值改为true。另一方面,顶点列表的索引值可以用于邻接矩阵,譬如顶点列表索引值为一的位置的元素也就是邻接矩阵第一行第一个或者第一列第一个表示的值。所以代码实现时在这里可以直接写
adjMatrix[index1][index2] = true, adjMartix[index2][index1] = true。
- 问题3:深度优先遍历的遍历顺序以及两种遍历的代码理解
- 问题3解决方案:广度优先遍历根据书上的代码已经很好理解了,从任意一个顶点开始,然后分别找该顶点相邻的顶点。但是深度优先遍历类似于前序遍历,这种情况下也是去找该顶点的左右顶点吗?
查阅资料,有人很形象地把深度优先遍历总结成了一句话“一路走到头,不撞墙不回头”,这个意思就是说,遍历以一个未被访问过的顶点作为起始顶点,沿当前顶点的边走到未访问过的顶点,当没有未访问过的顶点时,则回到上一个顶点,继续试探别的顶点,直到所有的顶点都被访问过。
以上图为例,以v1为起始顶点,首先走v2-->v4-->v8-->v5,然后没有可以访问的顶点了,返回到v1,再按照一路走到底的规则,走v3-->v6-->v7,遍历完成。
现在来看代码
public Iterator iteratorBFS(T startVertex) {
return iteratorBFS(getIndex(startVertex));
}//公有方法,同样是找到起始顶点在顶点列表中的索引
private Iterator iteratorBFS(int startIndex) {
Integer x;
Queue<Integer> tq = new LinkedQueue<Integer>();
UnorderedListADT<T> rls = new ArrayUnoderedQueue<T>();//广度优先遍历需要一个队列和一个无序列表
if (!indexIsValid(startIndex)) {
return rls.iterator();
}//判断索引值是否合法,如果不合法,返回一个rls的迭代,显示出来就是空
boolean[] visited = new boolean[numVertices];
for (int i = 0; i < numVertices; i++) {
visited[i] = false;
}//创建一个存储量为图的顶点数大小的布尔值数组,将数组内每一个值都设置为false,表示未访问过
tq.enqueue(new Integer(startIndex));//将起始顶点的值存在队列中
visited[startIndex] = true;//将起始顶点对应的在布尔值数组中的位置设为true,表示已访问
while (!tq.isEmpty()) {
// 出队列
x = tq.dequeue();
// 遍历记录表
rls.addToRear(vertices[x.intValue()]);//将每一个已访问的顶点值存入无序列表中
for (int i = 0; i < numVertices; i++) {
if (adjMatrix[x.intValue()][i] && !visited[i]) {//这里可以用邻接矩阵来表示它的相邻顶点,因为如果两个顶点是连通的的话,那么adjMatrix[x.intValue()][i]将会为true,所以这里的intValue方法应该也是定位数字的索引值
tq.enqueue(new Integer(i));
visited[i] = true;
}//将与该顶点相邻且未访问过的顶点按照之前的顺序,先存入队列中,然后将其在visited中的对应位置改为true,直到队列不为空,遍历结束
}
}
return new GraphIterator(rls.iterator());
深度优先遍历与广度优先遍历的代码思想基本是相同的,但前者运用的是栈,进出的原则不同所以输出的顺序有差别。同时,另一点区别是,在顶点尚未添加到无序列表之前,不会将顶点设置为已访问
代码调试中的问题和解决过程
-
问题1:关于最小生成树“mstNetwork”这一优雅算法的不优雅理解
-
问题1解决方案:最小生成树的实际意义就在于从复杂的网络中找到一条最便捷的路将所有顶点串起来,便捷的具体含义就是每条边的权重之和小于或等于同一图中任何其他生成树的权重之和,等于说明一个图中可能不止一个最小生成树。
代码理解
public Graph nstNetwork()
{
int x, y;
int index;
int weight;
int[] edge = new int[2];
HeapADT<Double> minHeap = new LinkedHeap<Double>();
Network<T> resultGraph = new Network<T>();
if (isEmpty() || !isConnected())
return resultGraph;//当图是空的或者没有连通的时候返回一个空的引用
resultGraph.adjMatrix = new boolean[numVertices][numVertices];//创建一个邻接矩阵
for (int i = 0; i < numVertices; i++)
for (int j = 0; j < numVertices; j++)
resultGraph.adjMatrix[i][j] = Double.POSITIVE_INFINITY;
resultGraph.vertices = (T[])(new Object[numVertices]);
boolean[] visited = new boolean[numVertices];
for (int i = 0; i < numVertices; i++)
visited[i] = false; //把所有的顶点都设置为未访问过的
edge[0] = 0;
resultGraph.vertices[0] = this.vertices[0];
resultGraph.numVertices++;
visited[0] = true;
// Add all edges that are adjacent to vertex 0 to the stack.
for (int i = 0; i < numVertices; i++)
{
minHeap.addElement(new Double(adjMatrix[0][i]))
}//将所有含起始顶点的边按照权重次序添加到最小堆中
while ((resultGraph.size() < this.size()) && !minHeap.isEmpty())
{
// Pop an edge off the stack and add it to the resultGraph.
do{
weight = (minHeap.removeMin()).doubleValue();
edge = getEdgeWithWeightOf(weight, visited);
}//从堆中取出最小边
while(!indexIsValid(edge[0]) || !indexIsValid(edge[1]));
x = edge[0];
y = edge[1];
if (!visited[x])
index = x;
if (!visited[y])
index = y;
//从最小边中的两个顶点中选出未访问的一个顶点,并将索引值赋给index
resultGraph.vertices[index] = this.vertices[index];
visited[index] = true;
resultGraph.numVertices++;//将新顶点的信息赋给相应数组
resultGraph.adjMatrix[x][y] = this.adjMatrix[x][y];
resultGraph.adjMatrix[y][x] = this.adjMatrix[y][x];
// 添加所有含该新顶点且另一顶点尚不在最小生成树中的边,直到最小树中包含图中的所有顶点或者最小堆中已经没有元素
for (int i = 0; i < numVertices; i++)
{
if (!visited[i] && this.adjMatrix[i][index] < Double.POSITIVE_INFINITY)
{
edge[0] = index;
edge[1] = i;
minHeap.addElement(new Double(adjMatrix[index][i]));
}
}
}
return resultGraph;
}
目前还不太能够理解edge[]的使用以及其中的部分代码所起的作用
按照教材给出的提示,edge[]似乎是,表示每条边的一个三元数组,其中包含起始顶点、终止顶点和权重,但是这里的定义又是int[] edge = new int[2],里面只包含了两个存储空间,照理说就不是用作存储边的数组了。包括其他一些代码的问题,比如一开始设置的resultGraph.adjMatrix[i][j] = Double.POSITIVE_INFINITY;是什么意思。算法的核心思想大概是理解了,代码实现好像还差的很远。
--- 分割线 ---
以上问题的回答有参照同学的博客以及与同学的讨论。
首先Double.POSITIVE_INFINITY表示的是无限大,resultGraph.adjMatrix[i][j] = Double.POSITIVE_INFINITY;在这里起到的作用,就和一个Boolean型的邻接矩阵,将它的初始值全部设置为false是一个道理。所以整个代码的前面一部分,全部是在定义实现最小生成树所需要的变量。除了刚才提到的邻接矩阵之外,还包含了一个存储访问信息的Boolean数组--visited,存储起始顶点和终止顶点索引值信息的数组edge,存储每一个顶点信息的数组resultGraph.vertices = (T[])(new Object[numVertices]);。
该最小生成树的生成的起始顶点,默认为了邻接矩阵的索引值为0的元素,所以首先设置
edge[0] = 0;
resultGraph.vertices[0] = this.vertices[0];
resultGraph.numVertices++;
visited[0] = true;
将所有数组都从起始顶点开始,利用for循环将含起始顶点的边的权重值依次添加进最小堆中,再依据最小堆的性质将权重最小的数弹出,据此找到相应的最小边,再根据最小边找到两个顶点中未访问的那一个顶点,并以此为新的起始顶点,去找下一个最小边,直到最小树中含有图中的所有顶点为止,也就是resultGraph.size() < this.size()) && !minHeap.isEmpty()时
以上的分析都是基于我自己的理解,有一些部分我也没琢磨明白,还有不完备的地方,希望多多指正
代码托管
上周考试错题总结
- Since a heap is a binary search tree, there is only one correct location for the insertion of a new node, and that is either the next open position from the left at level h or the first position on the left at level h+1 if level h is full.
A .True
B .Flase - 堆是一棵完全树,不是单纯的只是一棵二叉查找树
结对及互评
-
博客中值得学习的或问题:
- 教材学习内容都总结的很好,关于最小生成树的两个算法都做了很详细的解释,图片虽然做的丑但是很清晰,建议助教加分
-
基于评分标准,我给谭鑫的博客打分:5分。得分情况如下:
正确使用Markdown语法(加1分)
模板中的要素齐全(加1分)
教材学习中的问题和解决过程, 一个问题加1分
代码调试中的问题和解决过程, 两个问题加2分 -
基于评分标准,我给方艺雯的博客打分:8分。得分情况如下
正确使用Markdown语法(加1分):
模板中的要素齐全(加1分)
教材学习中的问题和解决过程, 两个问题加2分
代码调试中的问题和解决过程, 四个问题加4分 -
本周结对学习情况
-
上周博客互评情况
其他
书上的代码越来越不好理解了,然后本周开始要进行结对的小组编程,抱紧大腿,尽力跟上大家的步伐
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 8/8 | |
| 第二周 | 470/470 | 1/2 | 12/20 | |
| 第三周 | 685/1155 | 2/4 | 10/30 | |
| 第四周 | 2499/3654 | 2/6 | 12/42 | |
| 第六周 | 1218/4872 | 2/8 | 10/52 | |
| 第七周 | 590/5462 | 1/9 | 12/64 | |
| 第八周 | 993/6455 | 1/10 | 12/76 | |
| 第九周 | 1192/7467 | 2/12 | 10/86 | |
| 第十周 | 1375/8842 | 1/13 | 12/98 |


 浙公网安备 33010602011771号
浙公网安备 33010602011771号