密度估计-第3柱（二）

STEP 3：更新 均值 \(\mu_k,\ k=1,2,...,K\)

• 更新 GMM 的均值参数 \(\mu_k,\ \ k=1,2,...,K\)
• 通过责任 \(r_{nk}\) 更新，依赖于所有均值 \(\mu_k\)、协方差矩阵 \(\Sigma_k\)、混合权重 \(\pi_k\)，因此无法直接得到解析解
• \(\mu_k^{new}=\frac{\sum_{n=1}^{N}\ r_{nk}\ x_n}{|\sum_{m=1}^{N}\ r_{nk}|}=\frac{1}{|N_k|}\sum_{n=1}^{N}\ r_{nk}\ x_n\)
  • 责任 \(r_{nk}\) 的定义见 STEP 2(第 k 个模型参数对第 n 个数据点似然的影响)
  • \(N_k\) 指第 k 个混合分量对整个数据集的总责任 \(N_k\ := \sum_{m=1}^{N}\ r_{nk}\)
  • 直观理解：第 k 个混合分量相关联的数据点 \(x_n\) 的加权均值的蒙特卡洛估计，其中权重是责任 \(r_{nk}\)
• 数据点 \(x_n\) 的重要性权重是第 k 个簇对 \(x_n\) 的责任 \(r_{nk},\ k = 1,...,K\)
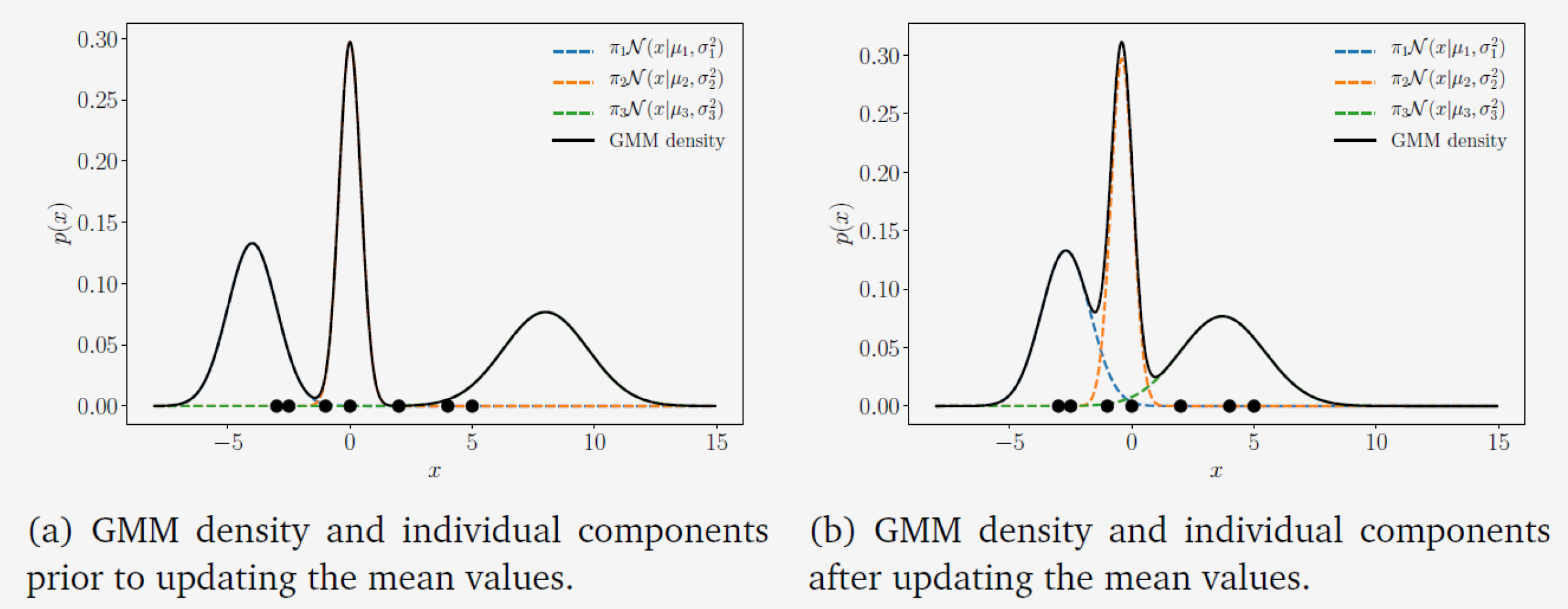
• 因此，均值 \(\mu_k\) 被拉向数据点 \(x_n\)，强度由 \(r_{nk}\) 给出
• 均值被更强地拉向那些相应混合分量具有高责任（即高似然）的数据点
  

STEP 4：更新 协方差矩阵 \(\Sigma_k,\ k=1,2,...,K\)

• 更新 GMM 的协方差参数 \(\Sigma_k,\ \ k=1,2,...,K\)
• \(\Sigma_k^{new}=\frac{1}{|N_k|} \sum_{n=1}^{N}\ r_{nk}(x_n-\mu_k)(x_n-\mu_k)^T\)
• 直观理解：第 k 个混合分量相关联的数据点 \(x_n\) 的加权协方差的蒙特卡洛估计，其中权重是责任 \(r_{nk}\)

STEP 5：更新 混合权重 \(pi_k,\ k=1,2,...,K\)

• \(\pi_k^{new}=\frac{N_k}{N}\)
  • N 是数据样本点的个数
• 直观理解：\(\pi_k\) 是第 k 个分布的总责任与数据点总数量的比率，即：第 k 个混合分量对数据集的相对重要性
• 显然，由于 \(N =\sum_{k=1}^{K}\ N_k\)，数据点的总数量可以解释为所有混合分量的总责任