图模型

有向图模型

• 所有随机变量联合分布分解为变量子集的因子的乘积
• 节点 --> 随机变量 \(a, b, c\)
• 边 --> 变量之间的概率关系，例如，条件概率

图语义

• a 到 b 的箭头（a是条件）表示条件概率 \(p(b|a)\)
• 全连接（对神经网络而言）
  • 假设3个输入节点，2个输出节点，全连接会有 \(2x3=6\) 条有向边
• 2条性质：
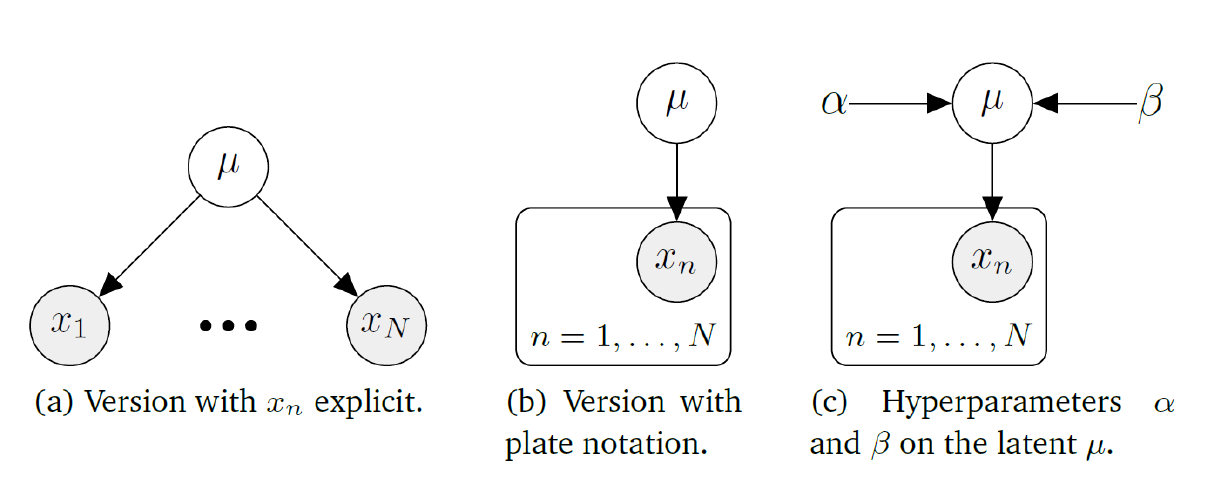
  • 我们寻求的联合分布 \(p(x_1,..., x_5)\) 是图中每个节点对应条件分布的乘积，共需5个条件分布
  • 每个条件分布仅依赖于图中对应节点的父节点。例如，\(x_4\) 将条件于 \(x_2\)
• plate（方框）记号，内部重复n次
  

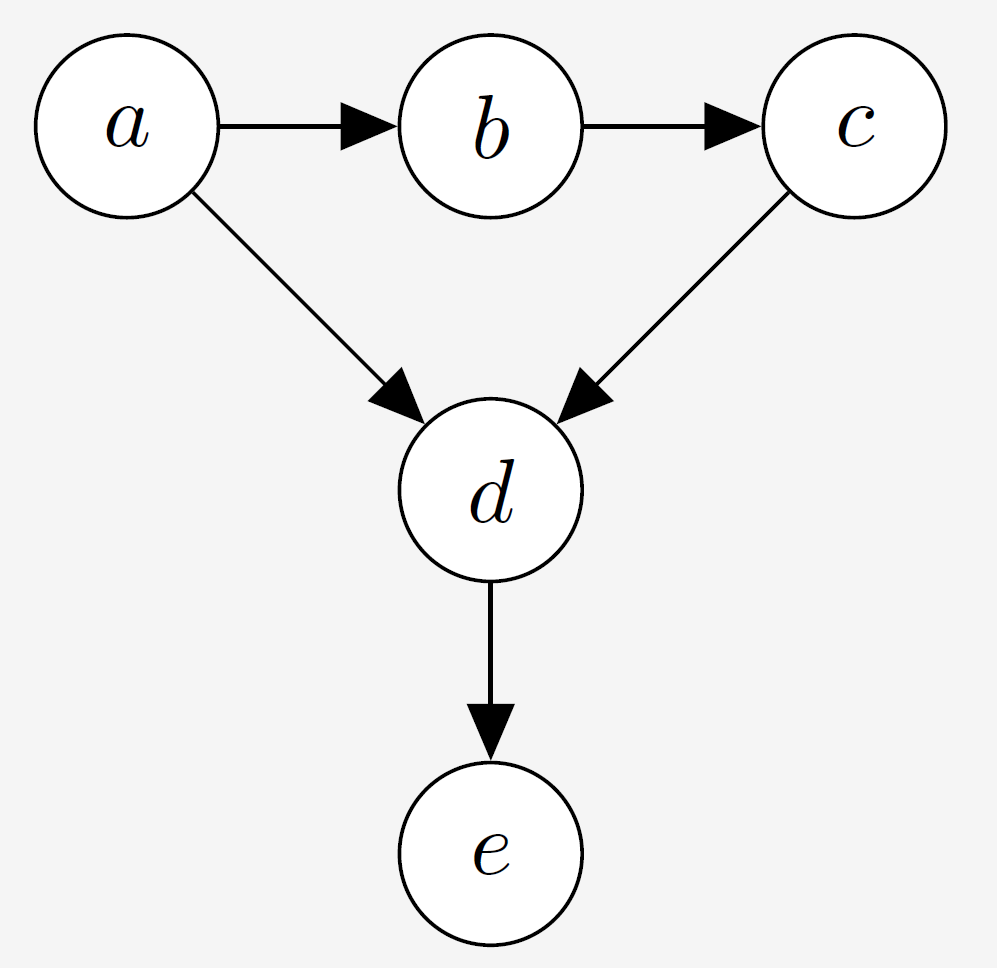
条件独立、d-分离

• \(A ⫫ B\ |\ C\) --> 给定 \(C\) 的条件下，\(A\) 与 \(B\) 条件独立
• d-分离
  • 两类：以某些节点为条件、不以某些节点为条件
  • 不以任何节点为条件
    • 即，条件 \(Z=\{\empty\}\)
    • 只有对撞节点（A-->W<--B）能够阻断路径
  • 以某组节点 \(Z\) 为条件
    • 某对撞节点（A-->W<--B）自身及其子孙节点都不在 \(Z\) 中
    • 链节点（A-->W-->B）或者分叉节点（A<--W-->B）在 \(Z\) 中
      

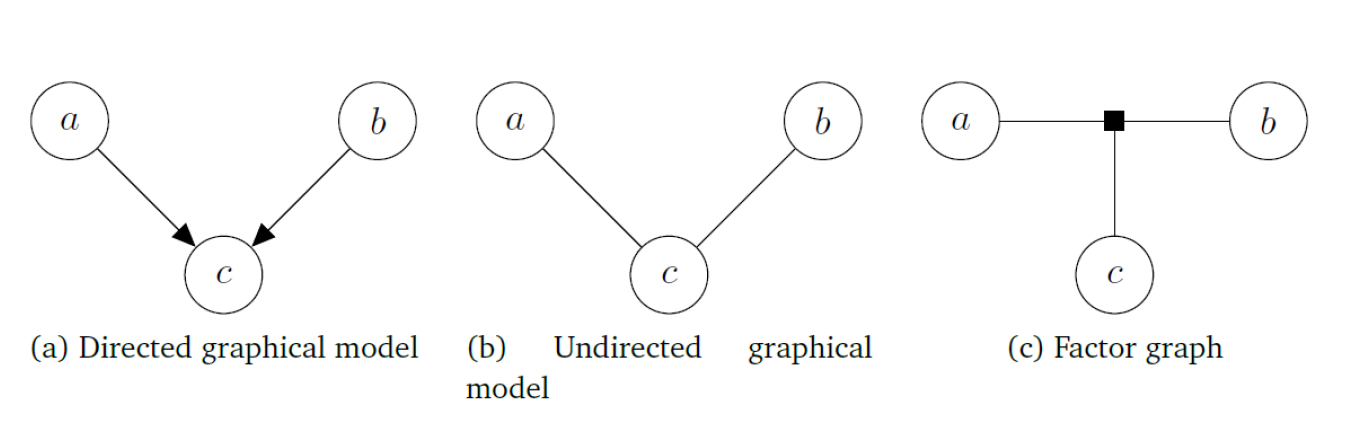
有向图、无向图、因子图

• 贝叶斯网络（有向）
• 马尔可夫随机场（无向）
• 因子图
  

似然、边缘似然的区别

• 似然容易过拟合，而边缘似然通常不会
• 因为模型参数已被边缘化(即无需拟合参数)
• 边缘似然会自动在模型复杂度与数据拟合之间进行权衡(奥卡姆剃刀)