参数估计（二）

正则化

• 经验风险最小化，可能出现过拟合，即：训练集风险估计值小，但测试集风险估计值大
• 引入一个惩罚项，来偏置经验风险最小化的搜索结果
• 通过添加额外项将参数偏向原点
• 附加一个正则项 \(||\theta||^2\)，和参数 \(\lambda\)
• 以最小二乘为例，在损失函数 \(L(\theta)\)后面添加一项 \(\lambda ||\theta||^2\)
• 发生过拟合时，参数 \(\lambda\) 往往会变得较大

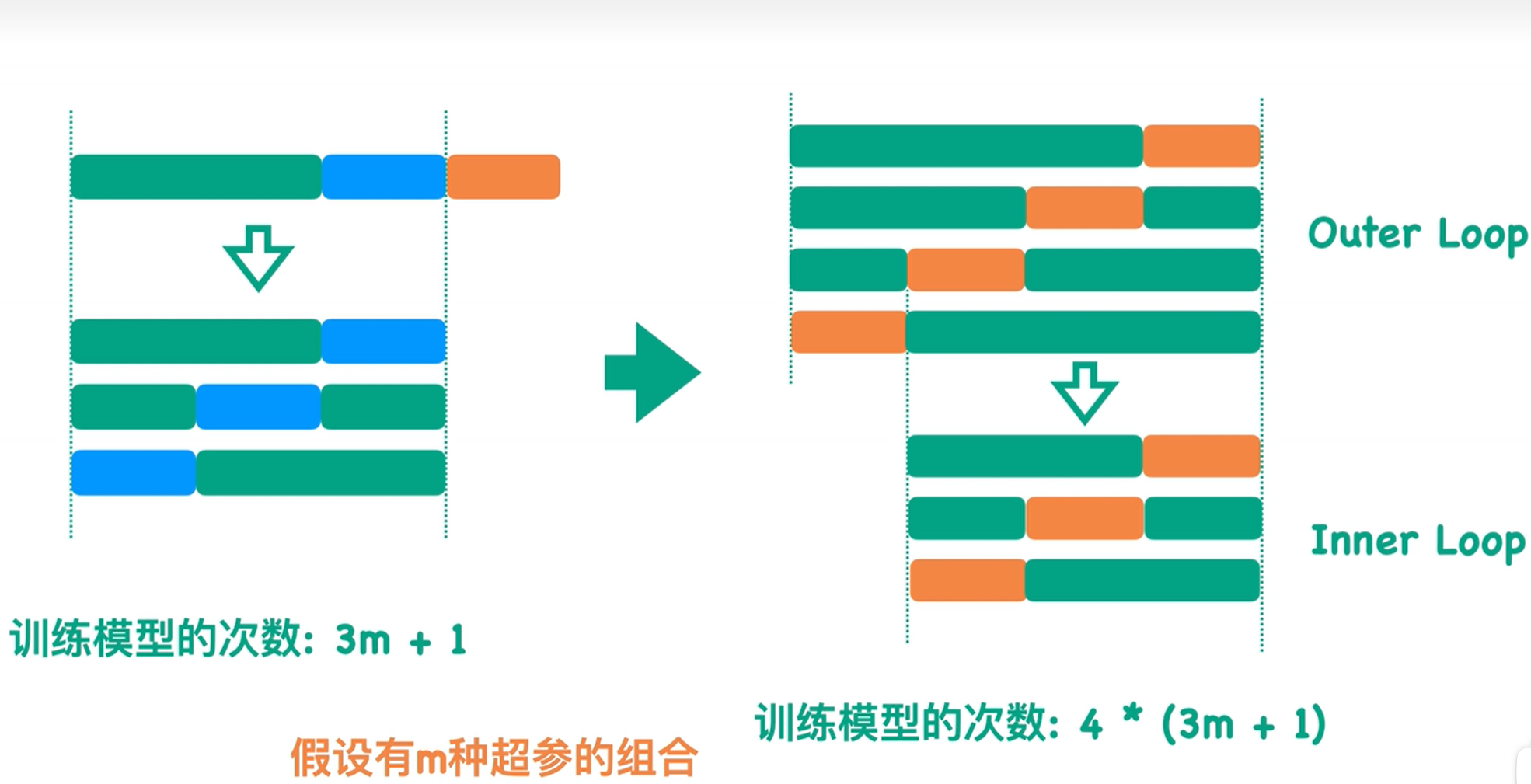
K折交叉验证、嵌套交叉验证

• 数据集有限，小数据集
  

最大似然估计

• 负对数形式
  -- 对数：连乘-->连加
  -- 负：最大-->最小，与凸优化理论统一
  -- 最大似然-->求解负对数的最小值
• 含义
  -- 似然函数取得最大值时的求解得到的参数 \(\theta\) 值，意味着在这个 \(\theta\) 取值下观测到样本 \(x_i\) 的概率最高
  -- 也就是说，用这个 \(\theta\) 取值构建的模型，最接近原本最真实的样子（样本数量越大，越接近）

最大后验估计（MAP）

• 基于贝叶斯公式，用于更新 \(\theta\)
• 负对数形式，要求的是最小值
• 含义
  -- 假设我知道参数 \(\theta\) 的概率，即所谓先验
  -- 乘以该参数下的似然函数 \(p(x|\theta)\) （给定参数 \(\theta\) 下 \(x\) 的条件概率）
  -- 除以真实的 \(x\) 的全概率，即所谓证据
  -- 得到关于参数 \(\theta\) 的新的概率，即所谓后验，参数已更新

贝叶斯推断

• 概率模型 --> 需要求解积分，得到的是参数的分布
• 最大似然ML、最大后验MAP --> 不用积分，直接最小化目标函数，得到的是参数的点估计值
• 必须为参数选择共轭先验，使先验与后验同分布
• 才能使贝叶斯框架中的积分能够解析求解
• 否则需要借助近似方法：随机近似、确定性近似、变分推断、期望传播