自适应控制

一.Lyapunov稳定性理论

（1）Lyapunov方程

\[A^{T}P+PA=-Q \]

二.正实函数

（1）正实

对于复变函数h(s): 当s为实数, h(s)为实数；当 Re(s)>=0 时，有 Re[h(s)] >=0. 那么我们称 h(s)为正实函数。

(2)严格正实

对于复变函数h(s): 当s为实数, h(s)为实数；当 Re(s) >= 0 时，有 Re[h(s)] >0. 那么我们称 h(s)为严格正实函数。


Hurwitz多项式:系数是正实数 ，其根位于复平面的左半平面或虚轴上，即根的实数部分是零或负的。

(3)Kalman-Yakubovich引理 (正实引理）

\[ \begin{cases} \dot{x}=Ax+Bu\\ y=Cx\\ \end{cases}\]

能观且能控，则对应传递函数

\[G(s)=C(sI-A)^{-1}B \]

为严格正实函数的充要条件：存在正定矩阵P和Q，使得

\[ \begin{cases} A^{T}P+PA=-Q, &Lyapunov稳定性定理\\ B^{T}P=C, &正实函数的要求\\ \end{cases}\]

三.Parks方法

Parks方法使用步骤：

（先验知识：\(A_p 、B_p\)的维数，确定m和n）
1.根据被控对象的结构选择参考模型\(A_m 、B_m\)
2.选择参数\(P、R_F、R_k\)(\(R_F\)和\(R_k\)是m×m矩阵)
3.采集实际系统的状态\(x_p(t)\)
4.根据输入\(y_r(t)\)计算参考模型的状态\(x_m(t)\)
5.更新反馈和前馈增益矩阵\(F\)、\(K\)

\[\begin{cases} \dot{F}=-R_FB_m^{T}Pex_p^{T}\\ \dot{K}=-R_kB_m^{T}Pey_r^{T}\\ \end{cases}\]

6.计算控制量u(t)

\[u(t)=F(t)x(t)+K(t)y_r(t) \]

simulink仿真

四.Narendra自适应控制器

Narendra于1978年提出采用前馈补偿器、反馈补偿器和一个可调增益构成自适应调节机构。 

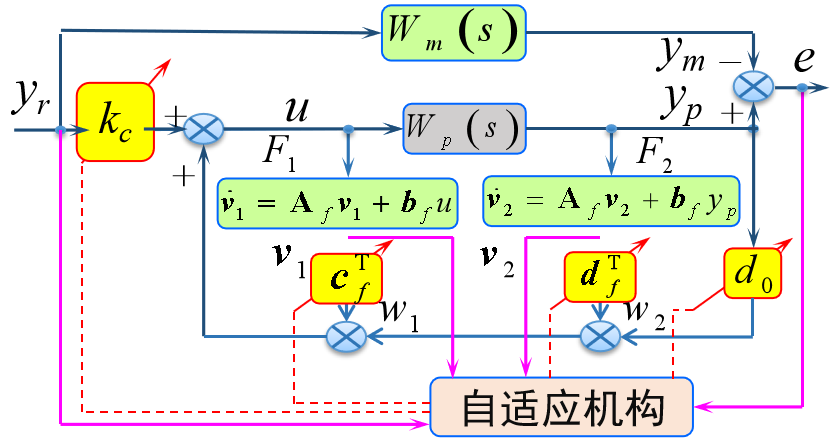
Narendra方法使用步骤：（先验知识：被控对象的阶次、相对阶）

参数向量

\[\theta=[k_c , c_f^{T}, d_0 , d_f^{T}]^{T} \]

信号向量

\[\varphi=[y_r,v_1^{T},y_p,v_2^{t}]^{T} \]

1.选择稳定、正实的参考模型传递函数\(W_m(s)\)
2.设置初值\(θ(0)\)、设置自适应增益矩阵\(Γ\)
3.采集实际系统的输出\(y_p(t)\)(\(θ\)是2n×1向量, \(Γ\)是2n×2n矩阵)
4.计算参考模型输出\(y_m(t)\)、计算输出误差\(e_1=y_p-y_m\)
5.更新两个滤波器的状态\(v1\)和\(v2\)

\[F_1:\begin{cases} \dot{v_1}=A_fv_1+B_fu\\ w_1=c_f^{T}v_1\\ \end{cases}\]

\[F_2:\begin{cases} \dot{v_2}=A_fv_2+B_fu\\ w_2=d_f^{T}v_2\\ \end{cases}\]

6.更新参数向量\(θ(t):\)$$\dot{\theta}=-e_1\Gamma\varphi$$
7.组建向量\(φ(t)\)，计算控制律\(u(t)\)

\[u(t)=\theta^{T}(t)\varphi(t) \]

被控对象相对阶为2

此时\(W_m(s)\)为非正实函数，引入Hurwitz多项式\(L(s)\)使得\(W_m(s)L(s)\)成为分母阶次比分子阶次高一阶的正实函数

\[L(s)=s+a(a>0) \]

\[D_f(s)=L(s)N_m(s) \]

可调参数自适应率：

\[\begin{cases} \dot{\theta}=-\Gamma\zeta(t)e_1(t)\\ \dot{\zeta}=-a\zeta(t)+\varphi(t)\\ \end{cases}\]

控制率：

\[u(t)=\theta^{T}\varphi+e_1\zeta^{T}\Gamma\zeta \]

五.基于Landau超稳定性理论设计MRAC

基于超稳定性理论设计要点：
（1）将MRACS等效为线性前向方块和非线性反馈方块所组成的闭环系统
（2）使等效前向方块满足正实性条件
（3）使等效反馈方块满足波波夫积分不等式
（4）由此确定合适的自适应规律

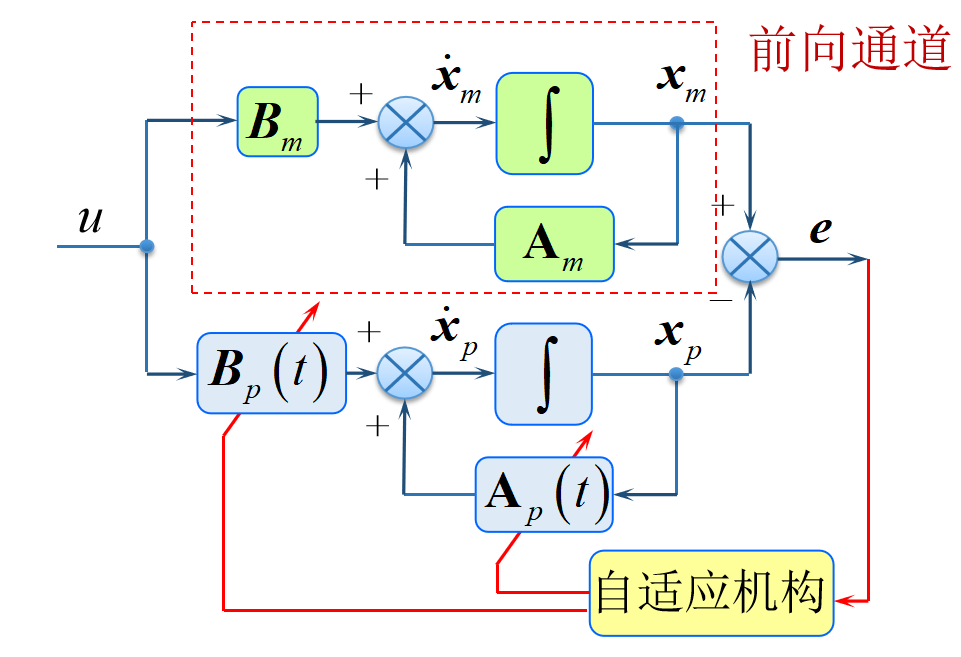
基于状态反馈方法

基于输入输出数据