提高图论大全
不废话,直接进入正题qwq。
1.无向图的DFS树
[CF962F] Simple Cycles Edges
题意:给定n点m边的无向图,找出所以边 \(u-v\),满足边 \(u-v\) 恰好在一个简单环上。(\(n\leq 10^5\))
题解:求一棵dfs树,一个环上的点要么都满足要么都不满足条件。枚举每条返祖边 \(u-v\),\(u-v\) 的链加 \(1\),最后看每个环(枚举每条返祖边)上边的权值是否都是1即可。
[BZOJ4238] 电压
题意:给定 \(n\) 点 \(m\) 边的无向图,找所有边 \(u-v\),使得删去它后,能将图二染色。(\(n\leq 10^5\))
题解:求一棵dfs树,如果原图中有两个及以上的奇环,没有边满足,否则那条返祖边满足。接下来考虑奇环上的树边,要求删掉这条边后,不出现新的奇环,即:不被任何一个偶环覆盖。树上差分即可。
Sabotage
题意:给定 \(n\) 个点 \(m\) 条边的DAG,定义无出度的点为关键点。\(q\) 次询问,给定点 \(u\) , \(v\),需要删掉一个点使得这两个点 均不能到达任意一个关键点,求删点的方案数。(\(n\leq 10^5\))
题解:先考虑一个点到所有关键点的必经点(所有到关键点的路径的交集),两个点求交集即可。对于不同的点 \(u\) 来说,前面每层的点都构成一个树形结构。现在维护一棵树,\(u\) 的父亲就是 \(u\) 能到的点(它们都在上一层,在树中的位置已经确定)的LCA。那么u到根路径上的点都是必经点。查询两个点时,答案就是它们在新树上LCA的深度。
2.欧拉路
[POJ1386] Play on Words
题意:给定n个单词,要求合适的顺序排成一排,使后一个单词的首字母等于前一个单词的末字母。
题解:一个字母抽象为一个点,连边一个单词的首字母和末字母,跑欧拉路即可。
3.哈密顿路
求法:设 \(f(i,S)\) 为当前在点 \(i\),经过的点集为 \(S\),枚举下一个点 \(j\) 转移即可。
4.最小生成树
[JSOI2008] 最小生成树计数
题意:求无向图 \(G\) 的最小生成树个数\(\mod 31011\). (\(n\leq 100\))
题解:随便求一棵最小生成树,枚举每种边权,将这种边权的 \(k\) 条边在图中删掉,得到若干个联通块。现在问题转化为:\(n\) 个点 \(m\) 条边,加入 \(k\) 条边使得图联通的方案数。\(Matrix\) 定理即可。
[USACO08OCT] 打井
题意:\(n\) 块农田,浇灌它可以从其他农田引水或者在这块农田上打井。在第 \(i\) 块地打井的代价为\(w_i\),连接农田 \(i,j\) 的代价为 \(p_{ij}\)。至少打一口井,求最小代价。
题解:至少打一口井就建新点 \(n+1\) ,向点 \(i\) 连边 \(w_i\),再加上农田间的边,求最小生成树即可。
[BZOJ3714] Kuglarz
题意:有 \(n\) 个杯子,有些下面可能藏着球,可以花 \(c_{ij}\) 元知道杯子 \(i\to j\) 下面藏球总数的奇偶性。求最少需要多少钱知道哪些杯子底下藏着球。
题解:记 \(a_i\) 为杯子 \(i\) 底下藏球个数,记 \(s_i\) 为 \(a\) 的前缀和。那么知道哪些杯子底下有球,等价于知道所有 \(s\) 值的奇偶性。连边 \((i,j,c_{ij})\) 表示若知道 \(i\),要知道 \(j\) 的代价为 \(c_{ij}\)。跑最小生成树即可。
[CF437D] The Child and Zoo
题意:给定 \(n\) 点 \(m\) 边的图,每个点有权值 \(a_i\)。对于每对点 \((u,v)\),选择一条 \(min\{a_i\}\)最大的路径,记这个值为 \(f(u,v)\)。求所有 \(f(u,v)\) 的平均值。
题解:首先点权化边权,边 \((u,v)\) 的边权为 \(min(a_u,a_v)\)。那么这条路径一定在最大生成树上。考虑每条边对答案的贡献,将最大生成树上的边按边权从小到大加入,用并查集维护每个联通块的大小,一条边的贡献即为:权值\(\times\)两边联通块大小的乘积。最后答案除以 \(n(n-1)\) 即可。
[BZOJ2395] [Balkan2011] Time is Money
题意:给定 \(n\) 点 \(m\) 边的图,每个点有两个非负权值 \(t_i,c_i\),求一棵生成树 \(T\),最小化
\(n\leq 200, m\leq 10000\)
题解:啥都不说了,秒题!好题!神题!orz。那就讲得详细些吧!
首先看到两个权值,想办法转化为二维平面上的问题。对于一棵生成树 \(T\),记 \(x\) 为 \(t\) 值和,\(y\) 为 \(c\) 值和,那么 \(T(x,y)\) 可以表示为平面上的一个点,权值为横纵坐标的乘积。
显然最左边点是以 \(t\) 构建最小生成树 \(P(x_1,y_1)\),最下边的点为以 \(c\) 构建最小生成树 \(Q(x_2,y_2)\)。\(PQ\)之间还会有些其他的生成树 \(S(x,y)\),形如下图:
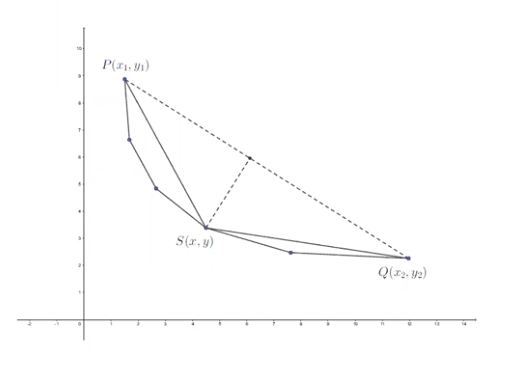
那么可能成为答案的点,一定构成了一个下凸壳,我们要将这个下凸壳求出来。
考虑分治,每次求一个在直线 \(PQ\) 下方,且距离直线最远的点 \(S\),然后左右半边接着做,直到下方没有点为止。可以证明,下凸壳上的点至多有 \(O(m^2)\) 个,而且远远达不到上界。
最后的问题是如何找到点 \(S\)。最大化 \(S\) 到 \(PQ\) 的距离等价于最大化三角形\(PSQ\) 的面积,等价于向量 \(SP\) 和向量 \(SQ\) 的叉积最大。即:
所以把没条边赋值为 \(w_i=(y_2-y_1)t_i-(x_2-x_1)c_i\),求最小生成树即可。
这道题运用了数形结合的思想,是不可多见的好题。
5.斯坦纳树
模板:[WC2008] 游览计划
习题:[LOJ2977] [THUSC2017] 巧克力
6.最短路
[POJ3613] Cow Relays
题意:给定 \(n\) 点 \(m\) 边的图,求 \(s\to t\) 恰好经过 \(k\) 条边的最短路的长度。\(n\leq 200,k\leq 10^6\)
题解:定义新矩阵乘法的规则为 \(Floyd\) 的规则,可以证明它满足结合律,矩阵快速幂即可。
[POJ1734] Sightseeing Trip
题意:带权无向图上求边权之和最小的简单环。\(n\leq 100\)
题解:一个环的表达:\(u\to...\to v\to k\to u\)。其中 \(k\) 不在 \(u\to v\) 的路径中出现,而 \(Floyd\) 每次加入一个新点,就可以满足这个条件,所以在 \(Floyd\) 的时候顺便更新下即可。
[POJ1860] Currency Exchange
题意:\(n\) 种货币,\(m\) 种兑换关系。每次兑换需要手续费,比如当你用\(100\)A币换B币时,A到B的汇率是 \(29.75\),手续费是 \(0.39\),那么你可以得到 \((100-0.39)\times 29.75\) B币。现在手上有 \(x\) 元S币,问经过兑换最后换回S币,金额数能否增加。
题解:每次向权值增大的方向拓展,\(SPFA\) 判是否存在正权回路即可。
[BZOJ2118] 墨墨的等式
题意:给定 \(n\),数列 \(\{a_n\}\),常数 \(B\) 的取值范围,求有多少个 \(B\) 使下面的等式存在非负整数解。
题解:如果 \(B\) 是一个可行解,那么 \(B+a_1, B+2a_1...\) 都是可行解。所以我们把 \(a_i\) 对 \(a_1\) 取模,那么我们只需要求一个最小的 \(B\) 满足上式,计算答案时再加上若干倍 \(a_1\) 获得其他解。对于 \(1\to a_1-1\)的每个数字 \(i\),枚举其他的 \(a_j\),连边 \((i,i+(a_j\mod a_1),a_j)\)。跑最短路即可求出最小的 \(B\)。
[经典构图] 区间覆盖
题意:\(n\) 个区间 \([L_i,R_i]\),代价 \(w_i\)。选出一些区间覆盖 \([1,n]\),最小化代价和。
题解:原问题等价于从 \(1\) 开始跳,每次可以往回跳,若当前的点 \(i=L_j\),可以花 \(w_j\) 的代价跳到 \(R_j+1\),问最少多少代价跳到 \(n+1\)。连边 \((i,i-1,0)\) 表示往回跳,连边 \((L_i,R_i+1,w_i)\) 表示跳一个区间。最短路即可。
差分约束系统
[ZJU1508] Interval
题意:有 \(0,1,2,...,m\) 共 \((m+1)\) 个整数,从中选一些。\(n\) 个要求,每个要求形如 \([l_i,r_i]\) 中选的数的个数不少于 \(c_i\)。最小化选出数的个数。 \(n\leq 5\times 10^4\)
题解:区间选的数的数量需要转化为差的形式,才能用差分约束,容易想到前缀和。记 si 为 1-i 这些数选了几个。那么一个要求即为 \(s_{r_i}-s_{l_i-1}\geq c_i\) ,还有一些很自然的约束:\(1\geq s_i-s_{i-1}\geq 0\)。连边 \((s_{r_i},s_{l_i-1},-c_i),(s_i,s_{i-1},0),(s_{i-1},s_{i},1)\),跑最短路最小化 \(s_m\) 即可。
[POJ1275] Cashier Employment
题意:一家 \(24\) 小时便利店,每个小时需要一定数量的出纳员,记为 \(R_1,R_2...R_{24}\),有 \(n\) 人申请这项工作,如果 \(i\) 被录用,他会从 \(t_i\) 时刻开始连续循环工作 \(8\) 个小时。最小化总出纳员数。\(n\leq 1000\)
题解:根据套路,记 \(num_i\) 为时刻 i 应聘的人数,si 为小时 1-i 实际录用的人数。应满足如下约束:
发现多了一项 \(s_{24}\),而我们想最小化它。所以从小到大枚举它的值,再用差分约束判断是否有解即可。
7.Tarjan
知识点:强连通分量,割点,桥,点双联通分量,边双联通分量,2-sat。
常见简单套路:缩点转 DAG,再利用DAG的性质dp或者干别的,相关习题:[TYVJ1936] 太空战队,[HDU2767] Proving Equivalences
[HNOI2012] 矿场搭建
题意:煤矿工地可以看成是由隧道连接挖煤点组成的无向图。为安全起见,希望在工地发生事故时所有挖煤点的工人都能有一条出路逃到救援出口处。于是矿主决定在某些挖煤点设立救援出口,使得无论哪一个挖煤点坍塌之后,其他挖煤点的工人都有一条道路通向救援出口。问至少需要设置几个救援出口,以及不同最少救援出口的设置方案总数。
题解:如果坍塌的不是割点,不会产生影响。删去所有的割点,得到若干联通块。若只有一个联通块(没有割点),需要两个即可(塌一个还有一个)。否则如果一个联通块,连接两个及以上的割点,不需要设置救援出口,否则需要一个。最后把所有联通块的答案合并下即可。
[POJ3177] Redundant Paths
题意:给定 \(n\) 点 \(m\) 边的无向图,求至少加入多少条边后,图是边双联通的。
题解:边双缩点,一定构成一棵树。记叶子的数量为 \(x\),答案就为\(\lceil \frac{x}{2}\rceil\)。
[HDU4612] Warm Up
题意:给定 \(n\) 点 \(m\) 边的无向图,问添加一条边后,桥最多能减少多少个。
题解:边双缩点构成树的直径就是答案。
2-sat 模板:[POJ3678] Katu Puzzle
8.二分图
若干定理:最小点覆盖=n-最大独立集=最小路径覆盖=最大匹配
[ZJOI2007] 矩阵游戏
题意:给定一个黑白矩阵,每次可以交换两行两列,问若干次操作后,能否使一条主对角线上的点都为黑点。
题解:同行同列的点,经过若干次交换后还是同行同列。所以问题转化为:能否找到 \(n\) 个不同行不同列的点。\(n\) 行建 \(n\) 个点,\(n\) 列建 \(n\) 个点,如果 \(a[i][j]\)是黑色的,连边 \(i\to j\),最后判断最大匹配是否等于 \(n\) 即可。
[SCOI2010] 游戏
题意:\(n\) 个装备,每个装备有两个属性,为每个装备选择一个属性,使得从 \(1\) 开始的连续属性最多。
题解:属性装备建两排点连边,从 \(1\) 开始动态加入属性,直到没有匹配即可。
[BZOJ2150] 部落战争
题意:给定 \(n\times m\) 的带障碍网格图。一次行动可以从一个未经过的点开始,向下方跳一个 \(r\times c\) 大小的矩形,问最少的行动次数,使得除障碍点外其他所有点都被经过。
题解:跳跃是有方向性的,所以构成一个DAG。求DAG的最小路径覆盖即可。具体方法可以参考这个部分——网络流。
9.结语
提高组图论的知识点非常杂,但是如果我们理解了每个算法的精髓,再难的问题也会迎刃而解——这需要时间和努力。努力让自己更强一点,哪怕,一点点......



 浙公网安备 33010602011771号
浙公网安备 33010602011771号