网络流
分类:最大流,费用流
算法:名称:Dinic(O(玄学)) 用途:求一个网络的最大流
流程:1.按照残量网络将图分层,2.dfs多路增广,若无法增广,print(ans),否则 goto 1. 。
名称:连续最短路算法(O(玄学)) 用途:求一个网络的费用流
流程:每次SPFA增广一条流量,计算答案,直到无法增广。
一些知识点
1.有负环,要先消圈。
2.最小割最大流定理:
割:去掉一个边集S,使得s->t不连通,边集S即为一个割。
定理:在一个网络中,最小割=最大流
证明:参见 http://www.cppblog.com/hongtaozhy/archive/2010/04/26/113604.html
3.最小割的必须边和可行边
定义id(x)为x在残量网络上哪个强连通分量。
可行边:原网络该边满流且 id(u)!=id(v)
必须边:在满足可行边的条件下,额外满足 id(u)=id(s), id(v)=id(t)
解释:若边(u,v)不满流,则割掉这条边后不能构成最小割。
若在残量网络上,存在u->v的路径,那么实际这两个点没有被割掉,仍然不能构成最小割。
若该边是可行边,但是 id(u)!=id(s) ,说明 u 与 s 之间还有边被割掉了,所以这条边可以不被割掉,v->t 同理,故该边不是必须边。
4.最大权闭合子图
模型:有向图G的子图V,若V中边均指向内部顶点,且V中点权和最大,则是最大权闭合子图。
5.最大密度子图
模型:选出无向图G的子图V,最大化 点数/边数 。
6.二元关系与最小割
模型:n个物品,选有a[i]的收益,不选有b[i]的收益。两两之间也有额外收益,即:同时选 x,y 有 w1 的收益,同时不选 x,y 有 w2 的收益,选 x 不选 y 有 w3 的收益,不选 x 选 y 有 w4 的收益,问如何选物品使得收益最大?
分析:可以先把所有的收益加起来,再减去最小割
放建图的模型:
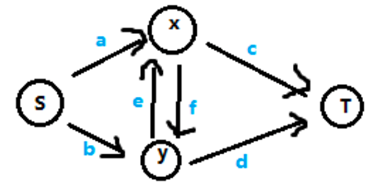
我们通过分析上图来确定 a,b,c,d,e,f 的流量。
我们规定与 s 相连的点为选择这个点,列方程如下:
w1(都选)=c+d
w2(都不选)=a+b
w3(选x不选y)=b+f+c
w4(不选x选y)=a+e+d
那么如何解这个方程组呢?
我们钦定 e=f , 解得 e=f=((w3+w4)-(w1+w2)) / 2
我们再钦定 a=0,就能解出 b,c,d 。
建图:那么求出每条边的流量,建图就如上图即可。
等等,如果 a,b,c,d 是负数咋办?举个例子:若a<0,我们就 c+=(-a) 通过这样一个对称一样的操作解决。
等等,如果 e,f 是负数咋办?我们可以把定义反一下,定义与 s 相连的点不选。但是这种方法只适用于没有奇环的图中(例如二分图),因为奇环的定义转换,转一圈回来就矛盾了。
题目:[Bzoj2127]happiness
我们把这题抽象为二元关系:每个同学抽象为一个物品,那么选有a1的收益,不选有b1的收益,前后左右同时选有sa的收益,同时不选有sb的收益,其他情况无收益。
一些量:w1=sa,w2=sb,w3=w4=0
e=f=((w3+w4)-(w1+w2))/2=((0+0)-(-sa-sb))/2=-(sa+sb)/2
哎呀!e=f<0 了,咋办?改变定义!方程组修改如下:
w1=c+d; w2=a+b; w3=b+f+c; w4=a+e+d;
解得:e=f=((w1+w2)-(w3+w4))/2=(sa+sb)/2. 欧耶!那么接下来算a,b,c,d.
钦定a=0, 那么 b=w2-a=sa, c=w3-b-f=-sa-(sa+sb)/2=(sb-sa)/2, d=w1-c=(sa-sb)/2 .
Nice!现在我们得到了所有的边权,若某个边权<0时,相信你也会处理了,快去快乐建图跑Dinic 吧!
练习:用这个模型建模型4和模型5。
7.网格图何时是二分图?
1.黑白染色
比如:网格中的每个格子与上下左右四个格子有边,那么这时我们要非常敏感地得出结论:这张图是二分图。
具体地,我们按如下方式染色:

即可。
2.行列
比如:网格图中可以安放一些十字射线,安放在第 i 行第 j 列的射线可以覆盖第 i 行和第 j 列,问最少放几个射线?
这个问题我们可以把行拉出来丢到左侧,列拉出来丢到右侧,若 (i,j) 可以安放射线,那么 add(i,j) ,最后就是一个二分图最小点覆盖问题。
8.[CTSC2015]性别改造计划
7.的应用。待更
9.上下界网络流
part1.无源汇可行流
建立超级源S,超级汇T,对于原图中的一条边 (i,j,low,up),连边 (S,j,low),(i,T,low),(i,j,up-low) 即可。
为什么是对的呢?因为 (i,T,low) 使得至少有 low 的流量流过,其他的流量可以经过 (i,j,up-low) 这条边流过,因为已经有 low 的流量分流向 T 了,所以我们再补上 (S,j,low),使其变为实际流量。
那么如何判断可行呢?很简单,只要判断所有和 T 相连的边是否满流即可。
一个例子:
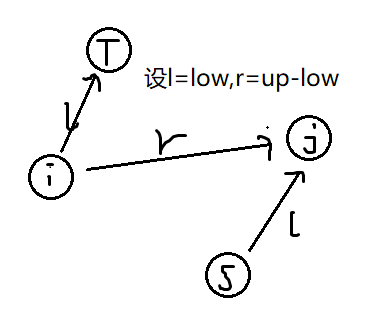
part2.有源汇最大/小流(方法1)
二分x,连边(T,S,x,INF),这样就转化成了一个无源汇可行流问题,利用part1的方法check即可。
part3.有源汇最大流(方法2)
连边(T,S,0,INF),跑一遍无源汇可行流,记录最后这条边的值ans1。
接着删掉这条边,再在残量网络上跑S->T最大流,记答案为ans2,则ans=ans1+ans2。
注意,删掉这条边的同时,要把求可行流时的超级源和超级汇同时删掉。
part4.有源汇最小流2(方法2)
先不连边(T,S,0,INF),按照part1.的方法,添加超级源和超级汇,连边跑最大流。
再添加这条边,跑超级源到超级汇的最大流,最后这条边的流量即为所求。
解释:当然,part3.和part4.是在有可行流的情况下才有意义,如果在每个part后面加个费用,那么就把Dinic换成连续最短路算法即可。
例题:[NOI2008]志愿者招募
这道题的主流算法是线性规划的单纯性法,当然,如果你不了解那东西,可以用网络流来解决。
具体地,我们根据套路,因为每类志愿者是独立的,所以一个志愿者代表一个流量。
那么每天至少 ai 个志愿者,就可以把每天建成一个点,每个点前的那条边代表那天的限制。
现在连边就呼之欲出了,连边 (i-1,i,a[i],INF,0) 表示第 i 天至少要 a[i] 个志愿者。
接着看,每类志愿者只会在 l -> r 这几天工作,志愿者有无限多个,招募费用 ci,那就连边 (r,l-1,0,INF,ci) 呗!
那么这里为啥不连边 (l-1,r,0,INF,ci) 呢?因为我们的目的是让 l-1 -> r 这些点之间的边增加 1 的流量,我们从 r 流到 l-1, 又从 l-1 流到 r ,这样一个循环,就增加了 1 的流量,而 (l-1,r) 这种连边直接跳过了,自然一点用处都没有。
那就,做完了?Of course!快去快乐地写一个上下界最小费用流吧!
10.最大费用流
把连续最短路算法的结束条件改成:if(maxdata<0)return; 即可。
在这里顺便说一下费用流的一个性质:费用流的费用是递增的,即 spfa 的运行结果会越来越大。
11.二分图
part1.判定:二分图染色。
part2.求最大匹配的算法:匈牙利算法,Dinic
part3.若干定理:二分图最大独立集=点数-最大匹配
二分图最小点覆盖=最大匹配
附. Dinic 求解最大匹配的建图
建立源点 s,汇点 t,原图中的边流量为 1,对于左部点,连边 (s,x,INF),对于右部点,连边 (x,t,INF),其实流量是一个大于等于 1 的整数即可,然后跑最大流即为所求。
12.DAG最小路径覆盖
拆点,若原图中有边 (u,v),则连边 (u,v'),DAG的最小路径覆盖=DAG上的点数 - 新图的最大匹配。
而我们发现新图是一张二分图,Dinic 可以在 O(nsqrt(n)) 的时间内解决。
13.无向图最小割(最小割树)
这类问题是这样的:给定一张n个点无向图(n<=500),q 次询问(q<=1e5),每次询问两点之间的最小割。
那么一个暴力的想法是:每次询问,建图Dinic跑一遍 u->v 的最小割,这样肯定会 TLE,那么我们能不能预处理这个东西呢?
我们来构造一棵最小割树:树上的一条边 (u,v) 的权值为无向图中 u->v 的最小割,那么这棵最小割树的性质为:无向图中,两点之间的最小割等于这两点在最小割树上路径中,边权的最小值。
我们先来构造这样一棵最小割树:
构造过程非常简单,只需要随便取两个点求它们的最小割,接着按照这个最小割的结果,把集合分成两部分,递归地做下去即可。
接下来你会问:纳尼?你连选点都不讲究,这个东西怎么可能的对的?如果你想知道为什么,可以去看下面这篇 blog,有详细的证明和实现。
https://www.luogu.com.cn/blog/user38148/solution-p4897
14.总结
本篇文章主要介绍了 OI 中网络流的相关知识,适合已经了解了算法的同学进行巩固和复习。
另外,本篇 blog 因时间原因,习题较少,但是之后笔者一定会尽量添加的。
最后,感谢帮我答疑解惑的 租酥雨老师,和集训时讲解知识的 张若天老师 。因为笔者能力有限,有不妥之处请提出您的宝贵建议。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号