学习笔记 带权并查集

 

 

今天的蒟蒻Lbmttw_lx又要学习新的有趣的东西了！

.

 

最近考的NOIP基础知识里面涉及到了一个比较有趣的东西，叫做带权并查集，可是Lbmttw_lx并不知道是什么，所以今天痛下决心好好学一下

正文分割线

---

 

 

　　理解权值并查集我们首先需要知道并查集是什么，在这里简单说一下吧

 

　　普通并查集的主要作用是判断图是否连通，即两个节点之间是否存在某种联系（即同一个根节点），如下图所示就是一个很普通的并查集，只能看到边代表着方向额而没有记录其他信息

 

　　代码应该都会写，不上了

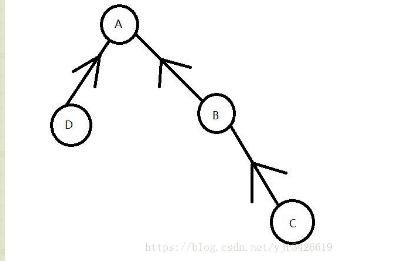
　　但是有些时候我们需要判断更多的信息，比如把多个连通的图合并为一个图并且记录合并后节点的个数，我们就需要一个更为高级的结构，权值并查集

 

　　如何理解这个权值呢？这个权值的意思就是需要额外记录一些信息。

　　

　　基于对并查集的理解，我们会发现一个比较有趣的事情，就是

 

　　看上面的图，我们对C进行find操作，让c连上A，不过在此之前，C会先找到B，然后才连上A，我们可不可以直接把C和A相连呢，这样极大程度上缩小了时间复杂度，得到的结果如下

 

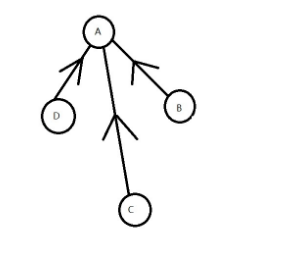
　　这种优化有一个学名，叫做并查集的路径压缩，将每一个节点直接与其find操作得到的节点连接。

 

　　很轻松的可以写出这样的代码

int find(int x)
{
    if (x != f[x])
    {
        f[x] = find(f[x]);
    }
    return f[x];
}

 

 　　和一般的并查集相比，这个不过是多了一个在find前面加了一个赋值操作，把所有要找的节点的根节点设成最后找到的那个点而已！！！但是就比之前的传统并查集优秀

 

　　基于路径压缩的原理，权值并查集就变成了一下的样子

 

　　

　　发现这个图，每一条边都记录了一条信息，具体记录什么信息需要依据题意而定，in general 都是一些边的相对关系。但是最主要的是，有权值就会有几个问题

 

　　1.由于我们优秀的路径压缩操作，所以我们记录的权值都是与根节点之间的权值，在我们find操作中，路径压缩也要更新这个权值

 

　　2.在并查集的合并操作中，我们也需要更新权值，因为根节点！！！路径压缩存储的是与根节点之间的权值！！！

 

　　所以呢，路径压缩的权值修改和并查集合并操作更新权值代码部分如下

 

　　（合并并查集）

    x=read(),y=read();
    int fx=find(x);
    int fy=find(y);
    if(fy!=fx)
    {
        f[fx]=fy;
        sum[fx]=num[fy];
        num[fy]+=num[fx];
    }

　　（路径压缩权值修改）

int find(int x)
{
    if(x==f[x])
    return x;
    int fa=find(f[x]);
    sum[x]+=sum[f[x]];
    return f[x]=fa;
}

 

 　　是不是非常简单呢？？

 

　　23333上两道例题

　　

　　题目描述

　　约翰所在的乡村可以看做一个二维平面，其中有 NNN 座牧场，每座牧场都有自己的坐标，编号为 111 到 NNN。牧场间存在一些道路，每条道路道路连接两个不同的牧场，方向必定平行于 XXX 轴或 YYY 轴。乡下地方的道路不会太多，连通两座牧场之间的路径是唯一的。

　　突然间，约翰的导航仪失灵了，牧场的坐标记录全部消失了。所幸的是，约翰找到了表示道路的数据，可以通过这些信息得知牧场间的相对位置。但贝西有急事，在约翰工作到一半的时候就要知道一些牧场间的曼哈顿距离。这时，如果约翰能从找回的道路信息之间推算出答案，就会告诉贝西。请你帮助约翰来回答贝西的问题吧。(x1,y1) (x_1, y_1)(x​1​​,y​1​​) 和 (x2,y2)(x_2, y_2)(x​2​​,y​2​​) 间的曼哈顿距离定义为 $|x1-x2|+|y1-y2|。$

　　输入格式

　　第111行：两个分开的整数NNN和MMM.

　　第222到M+1M+1M+1行：每行包括4个分开的内容，${\mathrm{F1，F2，L，D分别描述两个农场的编号，道路的长度，F1F\_1F1到F2F\_2F2的方向N,E,S,WN,E,S,WN,E,S,W．}}^{}$

　　第M+2M+2M+2行：一个整数，KKK，表示问题个数．

　　第M+3M+3M+3到M+K+2M+K+2M+K+2行：每行表示一个问题，由3部分组成：${\mathrm{F1，F2，J．其中F1F\_1F1和F2F\_2F2表示两个被问及的农场．而J(1\le J\le M)J(1\backslash leq\; J\backslash leq\; M)J(1\le J\le M)表示问题提出的时刻．JJJ为111时，表示得知信息111但未得知信息222时．}}^{}$

　　输出格式

　　• 对每个询问，输出牧场间的曼哈顿距离，如果当时恢复的数据还不足以得知答案，输出 $-1。以换行符分隔答案$

　　样例

　　样例输入 1

　　7 6
　　1 6 13 E
　　6 3 9 E
　　3 5 7 S
　　4 1 3 N
　　2 4 20 W
　　4 7 2 S
　　3
　　1 6 1
　　1 4 3
　　2 6 6

　　样例输出 1

　　13
　　-1
　　10

　　数据范围与提示

　　样例解释1

　　在时刻1，约翰知道1到6的距离为13;
　　在时刻3，1到4的距离仍然不知道；
　　在时刻6，位置6向北3个距离，向西7个距离于位置2，所以距离为10.

 

　　

 

　　AC代码如下

　　

#include <bits/stdc++.h>
#define ll long long
#define res register 
#define MAXN 100050
using namespace std;
int f[MAXN],nx[MAXN],ny[MAXN];
int n,m,q;
char s[10];
int find(int x)
{
    int y=f[x];
    if(x!=f[x]) 
    f[x]=find(f[x]);
    nx[x]+=nx[y];
    ny[x]+=ny[y];
    return f[x];
}
struct Node
{
    int x,y,c,p;
    int ans;
    inline friend bool operator <(Node a,Node b)
    {
        return a.c<b.c;
    }
}t[40010],tt[50010];
bool cmp(Node a,Node b)
{
    return a.p<b.p;
}
ll read()
{
    int s=0,w=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){s=(s<<1)+(s<<3)+ch-48;ch=getchar();}
    return s*w;
}
int main()
{
    freopen("navigate.in","r",stdin);
    freopen("navigate.out","w",stdout);
    n=read(),m=read();
    for(res int i=1;i<=n;i++)
    f[i]=i,nx[i]=ny[i]=0;
    for(res int i=1;i<=m;i++)
    {
        int x,y,c;
        x=read(),y=read(),c=read();
        scanf("%s",s);
        t[i].x=x;
        t[i].y=y;
        t[i].c=c;
        if(s[0]=='E') 
        t[i].p=0;
        else if(s[0]=='W') 
        t[i].p=1;
        else if(s[0]=='N') 
        t[i].p=2;
        else 
        t[i].p=3;
    }
    q=read();
    for(res int i=1;i<=q;i++)
    {
        int x,y,c;
        x=read(),y=read(),c=read();
        tt[i].x=x;
        tt[i].y=y;
        tt[i].c=c;
        tt[i].p=i;
    }
    sort(tt+1,tt+1+q);
    int now=0;
    for(int i=1;i<=q;i++)
    {
        while(now<tt[i].c)
        {
            now++;
            int x=t[now].x,y=t[now].y,c=t[now].c;
            int ff=find(y);
            nx[ff]=-nx[y];
            ny[ff]=-ny[y];
            f[ff]=y;
            nx[y]=ny[y]=0;
            f[y]=x;
            if(t[now].p==0) 
            nx[y]=c;
            else if(t[now].p==1) 
            nx[y]=-c;
            else if(t[now].p==2) 
            ny[y]=c;
            else 
            ny[y]=-c;
        }
        int x=tt[i].x,y=tt[i].y;
        if(find(x)!=find(y)) tt[i].ans=-1;
        else
        {
            tt[i].ans=abs(nx[x]-nx[y])+abs(ny[x]-ny[y]);
        }
    }
    sort(tt+1,tt+1+q,cmp);
    for(int i=1;i<=q;i++) 
    printf("%d\n",tt[i].ans);
    return 0;
}