PA2021 部分题解

PA 2021 部分题解

「PA 2021」Oranżada

无解条件显然，若 $a_i$ 的种类数小于 $k$，那么输出 $-1$。

否则贪心的取前 $k$ 个不同的 $a_i$ 就好了。

具体细节看代码。

Code

---

「PA 2021」Od deski do deski

先考虑对于一个固定的序列，判断其是否合法。

设 $g_i$ 表示 $[1,i]$ 是否能被删除，那么如果存在一个 $j\in[1,i-1]$ 满足 $g_{j-1}=true$ 且 $a_i=a_j$。

也就是说，若一个位置 $a_i$ 满足前缀 $i-1$ 是合法的，那么再往后出现 $a_i$ 的位置代表的前缀都是合法的。我们称这样的值为特殊值。

于是可以从左到右扫描序列，记录当前前缀的特殊值集合 $S$，以及当前前缀是否合法。加入一个数时，若前缀合法，则加入的值会成为特殊值。可以通过集合 $S$ 直接判断新前缀是否合法。

接着考虑计数，可以发现计数时不关心特殊值集合 $S$ 具体是什么，只关心它的大小。因为通过上面的方法可知加入的数只关心其是否是特殊值。

记 $f_{i,j,0/1}$ 表示长度为 $i$，特殊值集合大小为 $j$，不合法/合法的序列个数。

转移需要分类讨论一下，共四种：

• 当前前缀合法，继续填特殊值依旧合法，并且特殊值数量不会增多。$f_{i,j,1}\times j\to f_{i+1,j,1}$。
• 当前前缀合法，但是填不是特殊值的值，那么将变的不合法且特殊值数量增加一。$f_{i,j,1}\times (m-j)\to f_{i+1,j+1,0}$。
• 当前前缀不合法，填一个特殊值，那么将变的合法且特殊值数量不会增多。$f_{i,j,0}\times j\to f_{i+1,j,1}$。
• 当前前缀不合法，填一个不是特殊值的值，那么依旧不合法且特殊值数量不会增多。$f_{i,j,0}\times (m-j)\to f_{i+1,j,0}$。

最终答案为 $\sum_{i}f_{n,i,1}$。

时间复杂度 $\mathcal O(n^2)$。

具体细节看代码。

Code

---

「PA 2021」Zbalansowane słowa

首先对于原题，字符集大小只有 $3$。

那么就有一种 $\mathcal O(2^{\Sigma}n)$ 的做法。

枚举字符集，然后构造和为 $0$。具体的，对于当前枚举的字符集，给前面的几个字母随一个权值，并给最后一个字母的权值设为前面几个字母权值和的相反数。

手写哈希即可做到 $\mathcal O(2^{\Sigma}n)$，但是我懒用了 map 所以多一只 $\log$，不过没有关系，足以通过原题了。

具体细节看代码。

Code

但是呢，字符集是可以开到 $26$ 的！！！

定义一个字符串的状态为它的字符集，即 $\texttt{aa}$ 的状态为 $100\cdots0$，$\texttt{abd}$ 的状态为 $1101000\cdots0$。

不难发现每个点作为左端点只有 $26$ 种状态，作为右端点也只有 $26$ 种状态。

设当前状态为 $S$，$len=\left|S\right|$。

给每个字母随一个 ull 范围的权值。

设当前状态的每个字母的权值和为 $sum$，字符串的权值前缀和为 $s_i$。

那么一个区间合法说明 $s_r-s_{l-1}=\dfrac{r-l+1}{len}\times sum$。

移项得 $s_{l-1}-\dfrac{l-1}{len}\times sum=s_r-\dfrac{r}{len}\times sum$，可以把条件再改一下，设 $X$ 是一个很大的数，则 $sum\times X+s_{l-1}-\dfrac{l-1}{len}\times sum=sum\times X+s_r-\dfrac{r}{len}\times sum$

记 $pre_{i}$ 表示 $i$ 前面字符集按最后一次出现的位置排序的顺序，$suf_{i}$ 表示 $i$ 后面字符集按第一次出现的位置排序的顺序。

拿字符串 $\texttt{abbcda}$ 举例。

则 $pre_{4}=\left\{c,b,a\right\},pre_{6}=\left\{a,d,c,b\right\},suf_{1}=\left\{a,b,c,d\right\},suf_{3}=\left\{b,c,d,a\right\}$。

设 $f_{i,j}$ 表示以 $i$ 为右端点，状态大小为 $j$ 的值，$g_{i,j}$ 是以 $i$ 为左端点，状态大小为 $j$ 的值。$f$ 的计算需要用到 $pre$，$g$ 的计算需要用到 $suf$。

那么最终就是从后往前枚举，插入右端点的值，查询左端点的值。

具体细节看代码。

Code

---

「PA 2021」Desant 2

首先有个很显然的暴力 DP，记 $f_i$ 表示前 $i$ 个数的答案，$sum_i$ 表示 $a$ 的前缀和。

那么 $f_{i}=\max(f_{i-1},f_{i-k}+sum_i-sum_{i-k})$。

这样复杂度是 $\mathcal O(nQ)$ 的。

但是可以借鉴一下 这题 的思路。

可以把 DP 的过程看成在图上遍历，当前是否选连出去两条边，$k$ 个点排成一列，可以连成类似这样一张图：

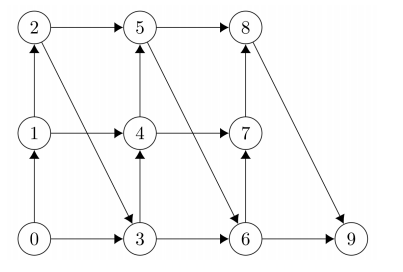
其中横向边的权值是区间和，纵向边的权值是 $0$。

记特殊边为 $2\to3,5\to6,8\to9$ 这种。

问题变为在图上查询最长路。

考虑分治，若行数不超过列数，考虑跨越中间列的询问一定经过中间列的点，对每个中间列的点求一遍所有点到其和其到所有点的最长路，即可处理这些询问，然后分治下去，复杂度 $\mathcal O(n\sqrt n)$。

否则，考虑跨越中间行的询问一定经过中间行的点，或者通过至少一条特殊边，对这些点边做一遍上一部分一样的过程即可，然后分治下去，复杂度 $\mathcal O(n\sqrt n)$。

细节有点多，可以看代码好好领悟。

Code

---

「PA 2021」Koszulki

简单贪心。

Code

---

「PA 2021」Pandemia

如果不考虑头部和尾部，那么我们设中间的连续为 $0$ 段的长度分别为 $a_1,a_2,\cdots,a_k$。那么贪心的，我们直接将 $a$ 按照降序排列，然后模拟。

那么如果考虑头部和尾部呢？

继续贪心，显然保护头部或尾部只需一个时间，那么我们在开头就保护。

上述贪心都是基于直觉，也不难证明是正确的（其实我不会证）。

具体细节看代码（自认为写的很丑）。

Code

---

「PA 2021」Poborcy podatkowi

我们考虑设 $f_{u,i}$ 表示的是以 $u$ 为根的子树，$u$ 留给父亲的链长为 $i$ 的已选边的边权之和最大值。

难点在于转移，考虑以 $f_{u,0}$ 为例，列举我们需要的条件：

• 接到这个点上的长度为 $1,3$ 的链的数量相同。
• 长度为 $2$ 的链的数量为偶数。

可以设 $g_{i,j}$ 表示选了长度为 $1$ 的链的个数减去长度为 $3$ 的个数为 $i$，长度为 $2$ 的链的数量的奇偶性为 $j$ 时所选边权的最大和。但是发现第一维是 $\mathcal O(n)$ 的，总复杂度为 $\mathcal O(n^2)$。

但是有个非常震撼的东西，将儿子序列随机打乱，就可以把第一维控制在 $\mathcal O(\sqrt n)$。

谁管证明啊（

具体细节看代码。

Code

---

「PA 2021」Zakłócenia

小清新构造，直觉上尽可能平均分是最优的，也不难证明是正确的。

Code

---

「PA 2021」Sumy

简单题，显然答案具有单调性，二分即可。

Code

---

「PA 2021」Mopadulo

设 $sum_{i}=(\sum\limits_{j=1}^{i}a_i)\bmod 10^9+7$，那么 $f_i$ 能被 $f_j,j\lt i$ 转移到需要满足以下任意一个条件：

• $sum_j\gt sum_i$ 且 $sum_j$ 与 $sum_i$ 奇偶性不同。
• $sum_j\le sum_i$ 且 $sum_j$ 与 $sum_i$ 奇偶性相同。

维护两个树状数组即可。

具体细节看代码。

Code

---

「PA 2021」Ranking sklepów internetowych

不难发现权值的最大值是 $2n+1$，计数的话就枚举区间长度，维护一下区间端点的合法区间就可以了。

具体细节看代码。

Code

---

「PA 2021」Butelki

比较震撼，直接 BFS 即可，因为状态数是线性的。

简单说明一下，考虑一次操作之后，必定有一个瓶子的状态为空或者满了。那么共 $6$ 种情况，对于每种情况，剩下两种瓶子的总量是固定的。所以状态数是线性的。

具体细节看代码。

Code

---

「PA 2021」Drzewo czerwono-czarne

更加震撼的一题。

先判掉一些平凡的 Case：

• $c=c^{′}$，输出 Yes
• $c$ 中只有一种颜色，输出 No
• $c^{′}$ 中，任意 $(u,v)\in E$ 都有 $c^{′}_{u}\ne c^{′}_{v}$，输出 No

前两个 Case 显然。第三个 Case 是由于我们最后一次操作的时候肯定会造出来两个相同颜色的点, 所以不可能没有这样的点对。

然后是最震撼的东西，如果存在一个度数 $\ge3$ 的点，输出 Yes。

因为我太菜，所以我暂时还没有完全看懂证明，所以这里贴一个 Qingyu 大佬的证明。（也可以看官方题解，不过看中文总比看波兰语翻译过来的要好吧。。）

否则原来的树就是一条链啦

• 如果序列开头的元素不一样, 那么我们只能把头给删掉, 因为我们只能merge 两个连续段, 不能 swap 或 split。
• 如果删掉以后，$c$ 的连续段数目 $\lt$ $c^{′}$ 的连续段数目就是 No，否则是 Yes。
• 证明仍然是类似的调整。注意到我们总是有一段的长度 $\ge 2$，所以我们一定可以通过伸缩一段让前面一段自由。

时间复杂度为 $\mathcal O(n)$。

具体细节看代码。

Code