JZOJ 5828. 【省选模拟2018.8.18】⽔果拼盘

---

这怕是假题

先看一看题解做法

---

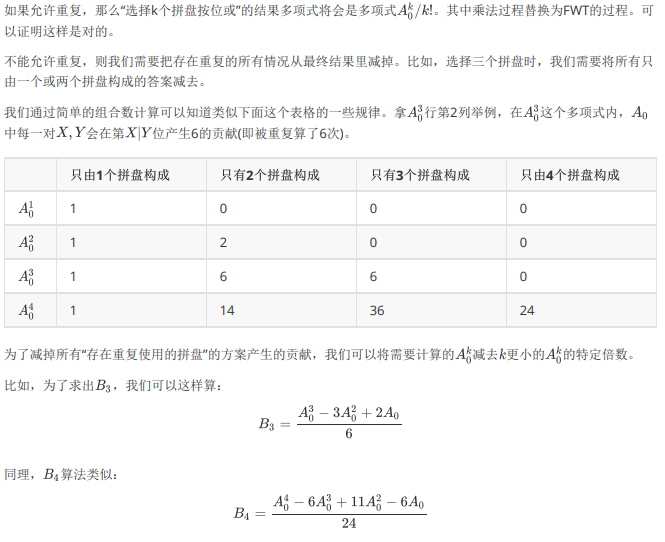
根据题意……显然每个水果是否能够进到最终选择的盘子里是相互独立的……

设$p_i$表示第$i$个水果最终被选到了，$cnt_i$表示第$i$个水果在多少个盘子中出现了

则有

$$1-p_i=\frac{n - cnt_i \choose k}{{n \choose k}}$$

即没有被选中的方案数相当于去掉这个水果后剩余盘子中拿出$k$个盘子的方案

之后答案就显得十分显然……$ans=\sum_{i=1}^{m}p_ia_i + (1-p_i)b_i$……

%:pragma GCC optimize(2)
%:pragma GCC optimize(3)
%:pragma GCC optimize("Ofast")
%:pragma GCC optimize("inline")
%:pragma GCC optimize("-fgcse")
%:pragma GCC optimize("-fgcse-lm")
%:pragma GCC optimize("-fipa-sra")
%:pragma GCC optimize("-ftree-pre")
%:pragma GCC optimize("-ftree-vrp")
%:pragma GCC optimize("-fpeephole2")
%:pragma GCC optimize("-ffast-math")
%:pragma GCC optimize("-fsched-spec")
%:pragma GCC optimize("unroll-loops")
%:pragma GCC optimize("-falign-jumps")
%:pragma GCC optimize("-falign-loops")
%:pragma GCC optimize("-falign-labels")
%:pragma GCC optimize("-fdevirtualize")
%:pragma GCC optimize("-fcaller-saves")
%:pragma GCC optimize("-fcrossjumping")
%:pragma GCC optimize("-fthread-jumps")
%:pragma GCC optimize("-funroll-loops")
%:pragma GCC optimize("-fwhole-program")
%:pragma GCC optimize("-freorder-blocks")
%:pragma GCC optimize("-fschedule-insns")
%:pragma GCC optimize("inline-functions")
%:pragma GCC optimize("-ftree-tail-merge")
%:pragma GCC optimize("-fschedule-insns2")
%:pragma GCC optimize("-fstrict-aliasing")
%:pragma GCC optimize("-fstrict-overflow")
%:pragma GCC optimize("-falign-functions")
%:pragma GCC optimize("-fcse-skip-blocks")
%:pragma GCC optimize("-fcse-follow-jumps")
%:pragma GCC optimize("-fsched-interblock")
%:pragma GCC optimize("-fpartial-inlining")
%:pragma GCC optimize("no-stack-protector")
%:pragma GCC optimize("-freorder-functions")
%:pragma GCC optimize("-findirect-inlining")
%:pragma GCC optimize("-fhoist-adjacent-loads")
%:pragma GCC optimize("-frerun-cse-after-loop")
%:pragma GCC optimize("inline-small-functions")
%:pragma GCC optimize("-finline-small-functions")
%:pragma GCC optimize("-ftree-switch-conversion")
%:pragma GCC optimize("-foptimize-sibling-calls")
%:pragma GCC optimize("-fexpensive-optimizations")
%:pragma GCC optimize("-funsafe-loop-optimizations")
%:pragma GCC optimize("inline-functions-called-once")
%:pragma GCC optimize("-fdelete-null-pointer-checks")

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10, mod = 998244353;
ll ans, fac[N], inv[N];
int n, m, k, a[N], b[N], cnt[N];
ll pw(ll a, ll b) {
    ll r = 1;
    for( ; b ; b >>= 1, a = a * a % mod) if(b & 1) r = r * a % mod;
    return r;
}

ll C(ll n, ll m) {
    if(m > n) return 0;
    return fac[n] * inv[m] % mod * inv[n - m] % mod;
}

int main() {
    freopen("eat.in", "r", stdin);
    freopen("eat.out", "w", stdout);
    scanf("%d%d%d", &n, &m, &k);
    fac[0] = inv[0] = 1;
    for(int i = 1 ; i <= n ; ++ i) fac[i] = fac[i - 1] * i % mod;
    for(int i = 1 ; i <= n ; ++ i) inv[i] = pw(fac[i], mod - 2);
    for(int i = 1 ; i <= m ; ++ i) scanf("%d", &a[i]);
    for(int i = 1 ; i <= m ; ++ i) scanf("%d", &b[i]);
    for(int i = 1, k ; i <= n ; ++ i) {
        scanf("%d", &k);
        for(int j = 1, x ; j <= k ; ++ j) {
            scanf("%d", &x);
            ++ cnt[x];
        }
    }
    for(int i = 1 ; i <= m ; ++ i) {
        ll nop = C(n - cnt[i], k) * pw(C(n, k), mod - 2) % mod;
        ll p = (1 - nop) % mod;
        ans = (ans + p * a[i] % mod) % mod;
        ans = (ans + nop * b[i] % mod) % mod;
    }
    ans = (ans % mod + mod) % mod;
    printf("%lld\n", ans);
}