USTC 形式化方法笔记 Formal Method
基础
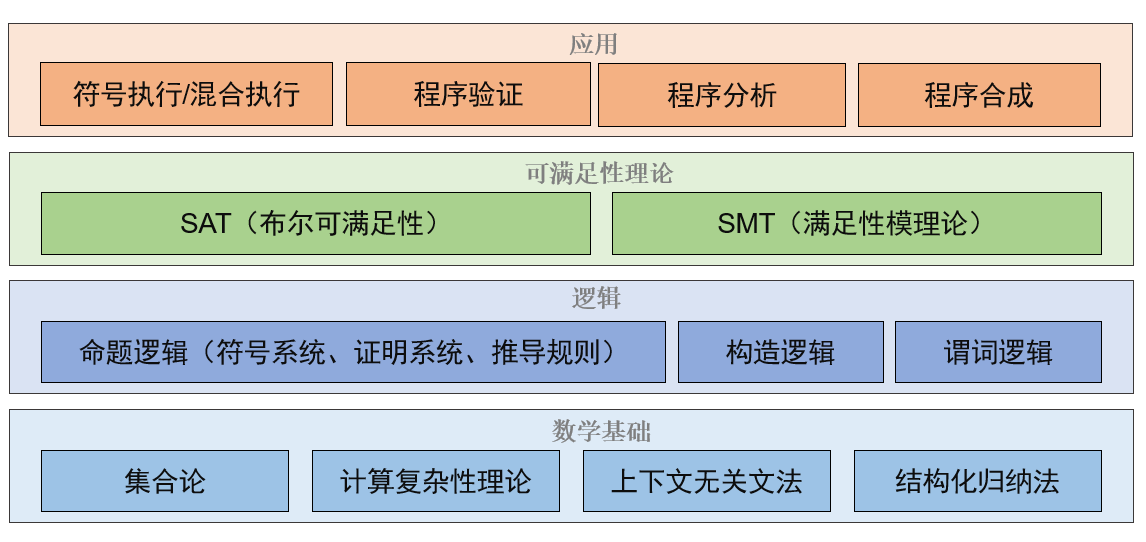
P 问题、NP 问题、NPC 问题
研究哪些问题能够被计算机计算的:
- P (Polynomial)问题:多项式时间 \(O(n^k)\) 可解决的问题
- NP(Non-Polynomial)问题:存在算法,至少要指数时间 \(O(2^n)\) 可解决的问题,不是现实可行
- NPC(NP-Complete)问题:NP 问题中最困难的一些问题;其他 NP 问题都能在多项式时间内转换成 NPC 问题,只要 NPC 问题能解,其他问题也可解
上下文无关文法
描述形式系统的符号工具
四元组: \(G = {N、T、S、P}\)
- \(N\) 是终结符集合
- \(T\) 是非终结符集合,且 \(N∩T = ∅\)
- \(S\) 是开始符号,且 \(S∈N\)
- \(P\) 是产生式的有限集合,每个产生式具有的形式如:\(N\to α,α ∈ (N ∪ T)*\)
【例题1】给定文法 G 的规则:
\(S ::= A\ B\ C\)
\(A ::= u\ |\ v\)
\(B ::= w\ |\ x\)
\(C ::= y\ |\ z\)
其中,终结符 N 的集合是 \(\{u, v, w, x, y, z\}\);非终结符 T 的集合是 \(\{S, A, B, C\}\);开始符号为非终结符 S,文法 G 的集合为 \(\{uwy, uwz, uxy, uxz, vwy, vwz, vxy, vxz\}\)
【例题2】给定文法 G 的规则:
\(E ::= E+E\ \mid\ E-E\ \mid\ E*E\ \mid\ E/E\ \mid\ (E)\ \mid\ n\)
其中,
终结符 N 的集合是 \(\{+,-,*,/,(),n\}\)
非终结符 T 的集合是 \(\{E\}\)
开始符号为非终结符 S,文法 G 的集合为整数域上加减乘除的表达式
【例题3】判断表达式 1+2*3 是否文法 G 的元素?
\(\begin{align}E & \to E + E \\ &\to E+E*E \\ &\to n-n*n\\ &\to1+2*3\end{align}\)
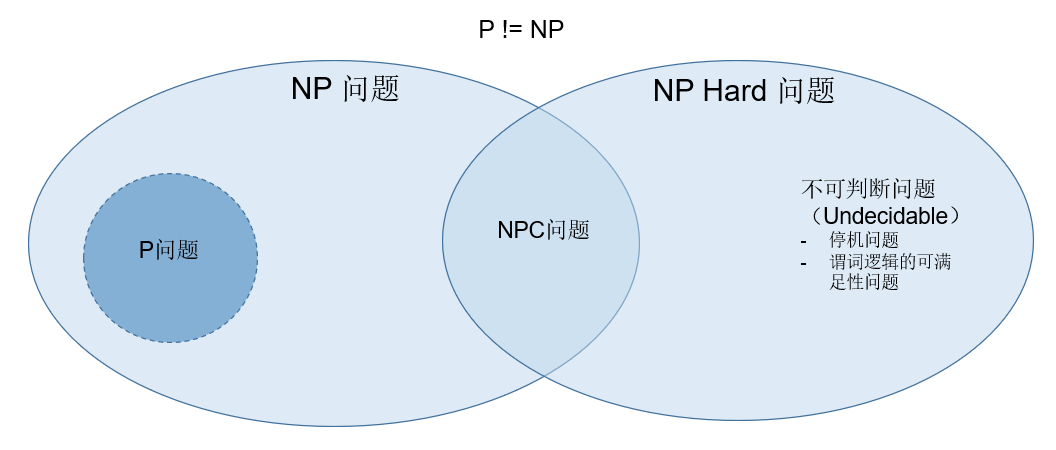
推导树(由于推导过程不唯一,推导树也不唯一):
结构归纳法
假设存在集合 \(A\),证明其具有某种性质 \(P\),只要证明:
- 归纳基础:集合 \(A\) 中的任意元素 \(x\) 都具有性质 \(P\),即 \(P(x)\) 成立。
- 归纳推理:设集合 \(A\) 中子集 \(B\) 具有性质 \(P\),即 \(P(B)\) 成立,如果由子集 \(B\) 递归构造的新集合\(C\),且 \(C \subseteq \ A\),仍具有性质 \(P\),即 \(P(C)\) 成立。
那么我们就可以推出,集合 \(A\) 具有性质 \(P\)。
【例题】证明以下给定文法所代表的集合 A,左括号和右括号的数量相等
\(E ::= E+E\ \mid\ E-E\ \mid\ E*E\ \mid\ E/E\ \mid\ (E)\ \mid\ n\)
证明:设 \(L(A)\) 和 \(R(A)\) 分别代表集合 \(A\) 的左括号数量和右括号数量
归纳基础:\(L(n) = R(n) = 0\)
归纳推理:设 \(L(E) = R(E)\) 成立,则
\(L(E+E) = L(E)+L(+)+L(E)=R(E)+R(+)+R(E) = R(E+E)\),成立;
同理可证 \(E-E\),\(E*E\),\(E/E\) 成立;
对 \((E)\) 进行验证可得:\(L((E)) = 1+L(E) = R(E)+1 = R((E))\),成立;
因此,\(L(A)=R(A)\)
命题逻辑 Propositional logic
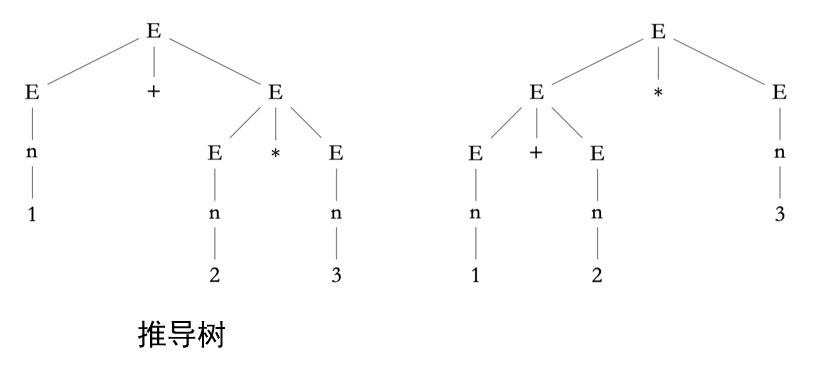
语法 Syntax
证明系统 The proof system
证明系统的目的就是去查实一个命题是否可证(provability)
证明系统在数学上:Hilbert 系统,构造性,没有规律可言,需要人为去推导
证明系统在CS上:自然演绎系统,可自动化推理,即算法
环境 $\Gamma $ :是由 \(n, n\ge 0\) 个命题构成的命题列表(特别的,若 n =0 称 \(\Gamma\) 为空环境)。在命题逻辑中,\(Γ\) 为一组逻辑命题,而在一阶逻辑中,\(Γ\) 是一组逻辑命题或变量。
\(\Gamma = P_1,...,P_n\)
断言 judgement \(⊢\) :是由环境 \(\Gamma\) 和命题 \(P\) 构成的元组
\(\Gamma\ ⊢ P\)
证明规则:是形如如下的一条公式,其中 \(n \ge 0\)
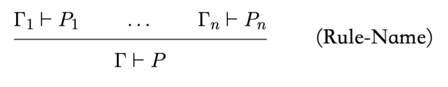
横线上方是前提,横线下方是结论
(1) 直接证明的结论 \(P\),已经存在前提条件中(公理)

(2) \(T\) 是无条件成立(公理)
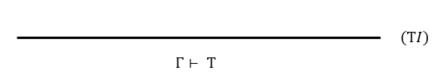
(3) \(⊥\),假 推出一切;也就是说从一组自相矛盾的条件出发,任何结论都成立。

(4) \(⋀\) 相关

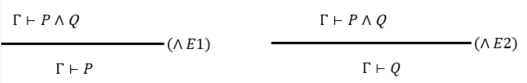
(5) \(⋁\) 相关


(6) \(\to\)

(7) \(¬\) 反证法

(8) \(¬¬\) 双重否定律(唯独该规则不是语法制导的)
命题逻辑由于存在非语法制导的规则,需要改进成构造逻辑的形式系统才可满足语法制导,从而才可以让计算机自动证明命题

【例题1】
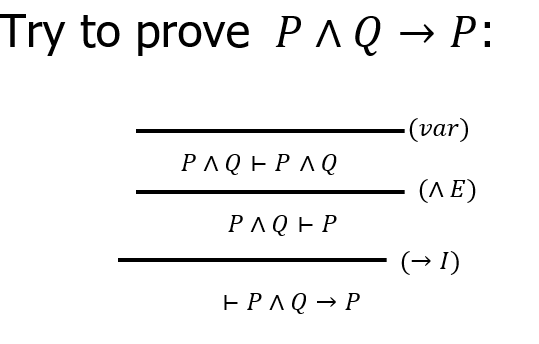
【例题2】$$P \rightarrow \neg \neg P$$
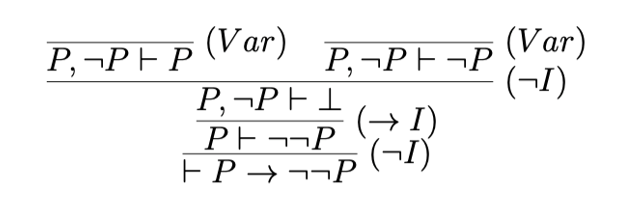
【例题3】\(⊢ (P\to R)\and (Q\to R)\to (P\and Q \to R)\)

【例题4】\(⊢ (P\to Q \and R)\to (P\to Q)\and (P\to R)\)

【例题5】\(⊢ (P\and (Q \and R))\to ((P\and Q)\and R)\)

【例题6】\(⊢\neg(P\or Q)\to (\neg P)\and (\neg Q)\)
语义系统 Semantics
证明系统 关心的是是否可证,而 语义系统 更关心计算,得到的结果是“真”还是“假”
但并不是所有问题都是可计算的,例如 NP 以及 NPC 问题
形式系统:

例如一个形式系统:真值表 The truth table
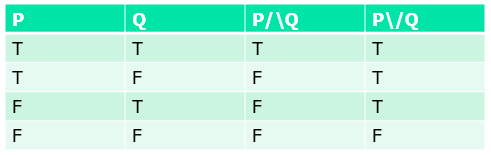
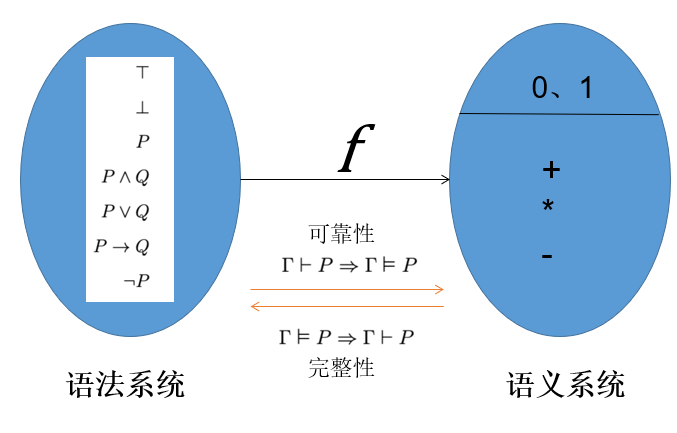
Interpretation:在以上两个形式系统 A B 中,A 即上文中研究的命题逻辑系统(逻辑命题,连接词,推理规则),B 即真值表系统(T,F,AND,OR);语义学本质上要写一个编译器 V,将 A 中的元素编译(即数学中映射\函数)到 B 中
也就是说把抽象的命题映射成某个代数系统的具体的值,就能计算出结果;实际上可以映射成真值表系统,也可以映射成布尔代数系统

重言式 Tautology (永真式):即对于任意的编译器 \(V\),\(V(P)=T\) ,使用 \(⊨P\) 来表示
\(⊢𝑃\) :(在证明系统中)语法上可证
\(⊨P\) :(在模型论中)通过计算为真
可靠性(Soundness):\(Γ⊢ P => Γ ⊨ P\)
完备性(Completeness):\(Γ ⊨ P => Γ⊢ P\)
构造逻辑 Constructive logic
构造逻辑的目的:避免排中律问题 \(⊢P⋁\sim P\)
例如一个排中律问题:无理数的无理数次幂是否可能是有理数?

语法 Syntax

和经典结构的语义相比,没有否定连接词,但是可以这样表示否定:\(¬P = P\to⊥\)
否定在构造系统中定义成语法糖(并不是必需的)
证明系统 The proof system
和命题逻辑差不多,就是删除掉了否定相关规则,即全部规则都可语法制导,从而可以实现证明系统的自动化推理
语义系统 Semantics
为了解决排中律问题,可以让 V 将 A 映射到 Heyting algebra,而不是到真值表系统或者布尔代数系统
谓词逻辑 Predicate logic
目的:为了让逻辑可以表示 “所有”、“存在” 谓词;而 ∀ 是多态的基础,∃ 是ADT的基础
语法 Syntax

-
Bound and free variables
对于 ∀𝑥.𝑃(𝑥, 𝑦) ,其中 x 为 bound var,y 为 free var
把自由变量(free variables)看作全局变量或外部变量
将替换看作函数调用
-
Substitution: P[x↦E]
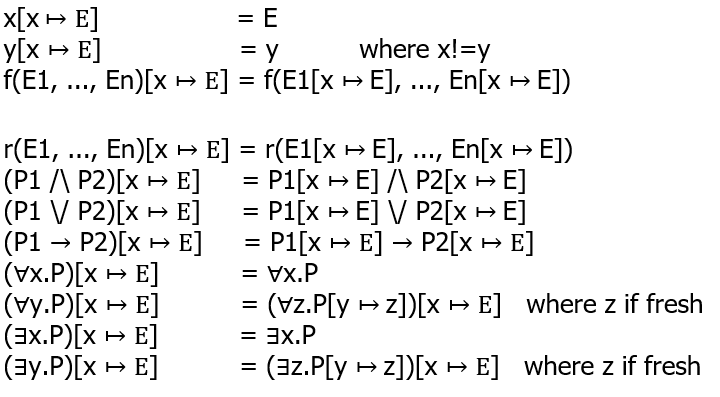
- 𝛼−renaming
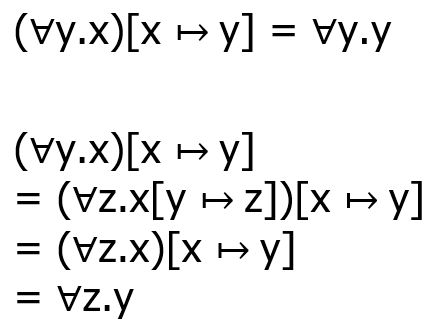
证明系统 The proof theory
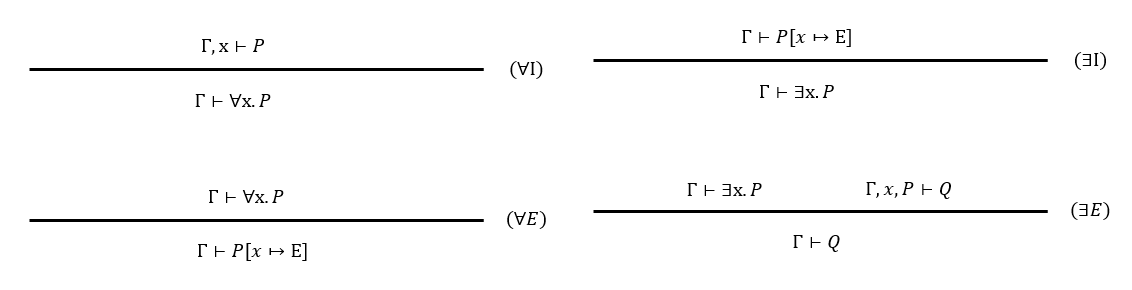
【例题1】\(\exist x.(P(x)\to ⊥)\to (\forall x.P(x)\to⊥)\)
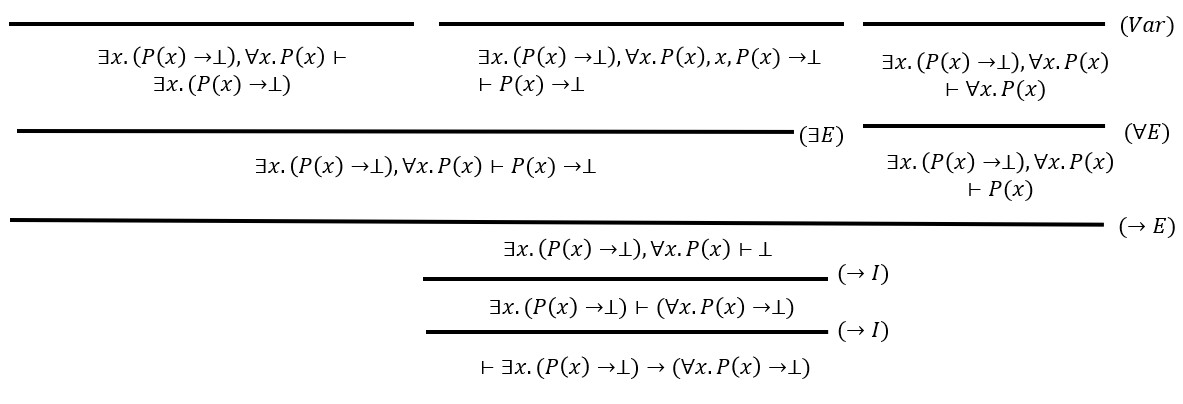
【例题2】\(\forall x.(P(x)\to Q(x))\to \exist x.P(x)\to\exist x.Q(x)\)
!
语义系统 Semantics
如果对于任意编译器 V和任意模型 M, \(\models_{V}^{\mathcal{M}} \mathrm{P}\) ,interpretation V and model M
如果 P 是有效的,可简化为 \(⊨P\)
可以一般化为 \(Γ ⊨P\)
可能有无限个模型 M,可能有无限种求值 V,甚至对于单个模型 M 也可能由无限多元素因为 \(\forall\)
Satisfiability(SAT 问题)
SAT:给定一个命题P,是否存在一个模型(变量的赋值)使得最终 P 为Ture
SAT 问题是第一个 NPC 问题
SAT 问题在实际问题的表达能力上局限性比较大,所以对 SAT 问题进行了扩展,通过把 SAT 问题与谓词逻辑或者说一阶逻辑结合,生成了一个新的理论,即可满足性模理论(satisfiablity modulo theory,SMT)。
而 SMT 问题即是判断 SMT 是否可满足问题
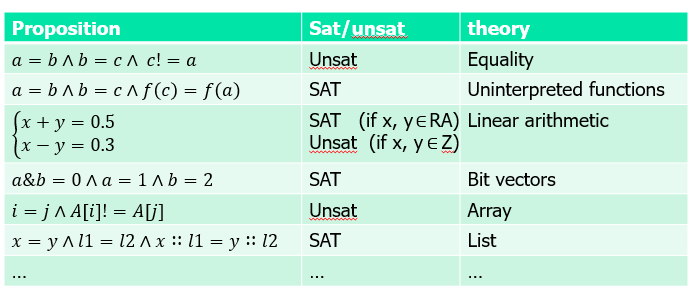
SAT 与 Valid
\(Vaild(P) ⟺ unsat(\sim P)\)
如果证明 \(P\) 为真,只需要证明 \(\sim P\) 为 UNSAT
Valid:在所有模型中,P 为真
SAT:在一个模型中,P 为真
DPLL 算法-转换范式
流程:\(P→NNF→CNF\)
【例题】
(1)否定范式 NNF
- 没有蕴含 \(\to\)
- 否定 \(\sim\) 只能出现在原子命题前
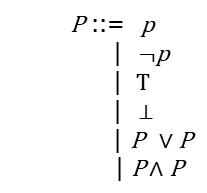
Non-NFF:\(p1⋀\sim (p2⋀p3)⋀\sim p4\)
NFF Example:\(p1⋀(\sim p2⋁\sim p3)⋀\sim p4\)
消除蕴含规则:
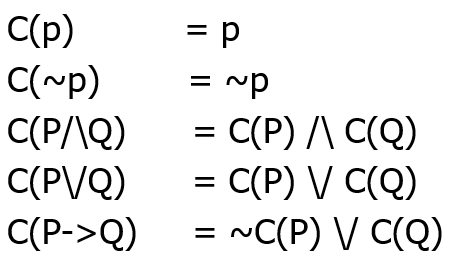
【例子】

转换成NFF规则(消去~非原子命题):
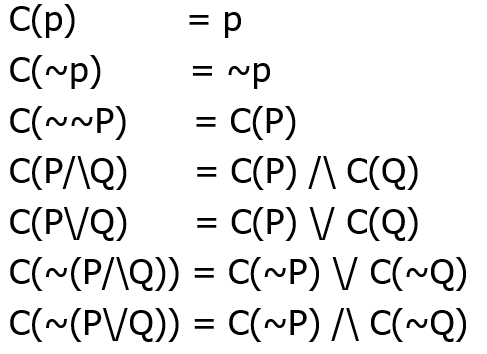
【例子】
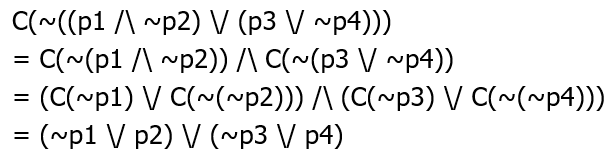
(2)CNF 合取范式

Non CNF:\((\sim p1⋀p2)⋁(\sim p2⋀ p4)\)
CNF Example:\((\sim p1⋁\sim p2)⋀(\sim p1⋁ p4)⋀(p2⋁p4)\)
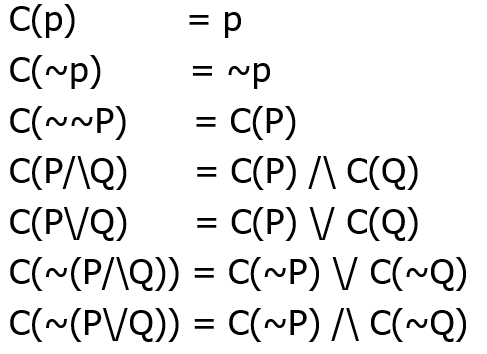
【例子】
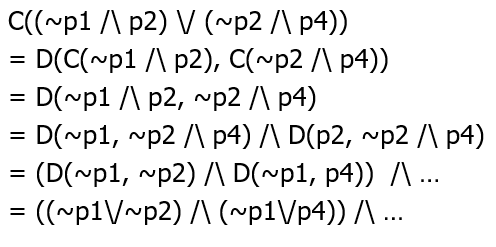
(3)DIMACS standard(可选的步骤)
如果当一个命题已经满足 CNF ,那么用数字代表一个命题进行编码
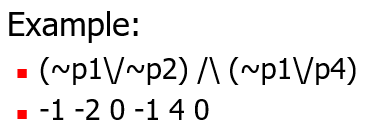
BCP 解析与传播

【例题】:

【例题】:

DPLL 算法改进
分割 Splitting:让 P 中的某个单元 prop 假设为真,分裂出两条简化路径
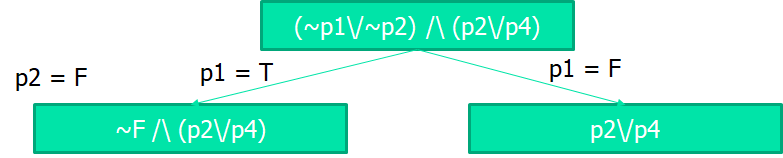
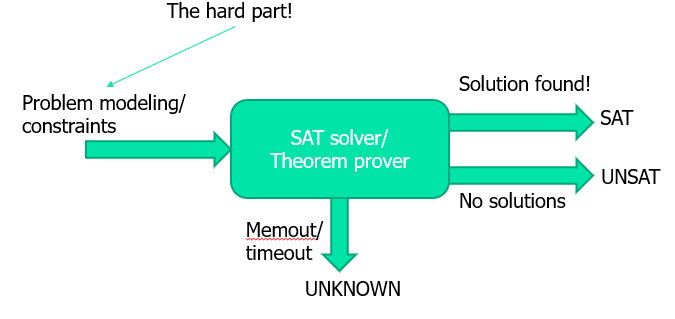
SAT 应用
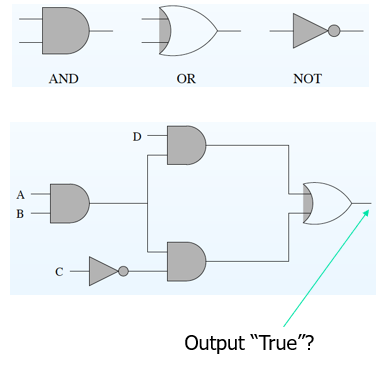
案例一(电路输出):可建模为
\(((A ⋀ B) ⋀ D) ⋁ ((A ⋀ B)⋀ \sim C)\)
案例二(坐椅子问题):可建模为
Ai: Alice takes seat Ai
Bi: Bob takes seat Bi
Ci: Bob take the seat Ci
Where 1<=i<=3
// constraint:
1. Alice must take just one seat:
(A1/\~A2/\~A3) \/ (~A1/\A2/\~A3) \/ (~A1/\~A2/\A3)
2. Bob (Carol) takes just one seat:
…
3. The 1st seat just taken by 1 person:
(A1/\~B1/\~C1) \/ (~A1/\B1/\~C1) \/ (~A1/\~B1/\C1)
4. Alice cannot sit near to Carol:
(A1->~B2)/\(A2->~B1)/\(A2->~B3)/\(A3->~B2)

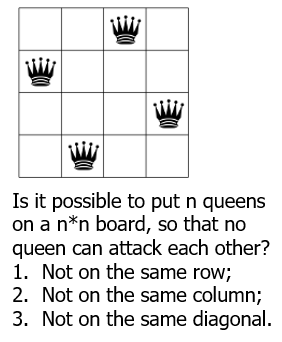
案例三(四皇后):可建模为
bool board[n][n]; // board[i][j]=true, when there is a queen; false, when there is not.
// constraint:
1.Every row has exactly 1 queen:
(b[0][0]/\~b[0][1]/\~b[0][2]/\~b[0][3]) \/ (~b[0][0]/\b[0][1]/\~b[0][2]/\~b[0][3]) \/ (~b[0][0]/\~b[0][1]/\b[0][2]/\~b[0][3]) \/ (~b[0][0]/\~b[0][1]/\~b[0][2]/\b[0][3])
…
2. Each column has exactly 1 queen:
...
3. Each diagonal has at most one queen:
...
语义系统 Semantics
可靠性与完备性依然成立!
可计算=可证,可证=可计算(计算机上可计算,不可判定为T还是F)
等式和未解释函数理论 EUF
目的: SAT 对于命题逻辑、NPC问题,但是已经高效(使用 DPLL 算法);但对于谓词逻辑,是不可判定的,不可能有计算机算法解决,不过将其限制到一个子集中:theory,可能是可解的
EUF 全称为 Equality and Uninterpreted Functions
EUF 理论

解决等式问题(Equality):
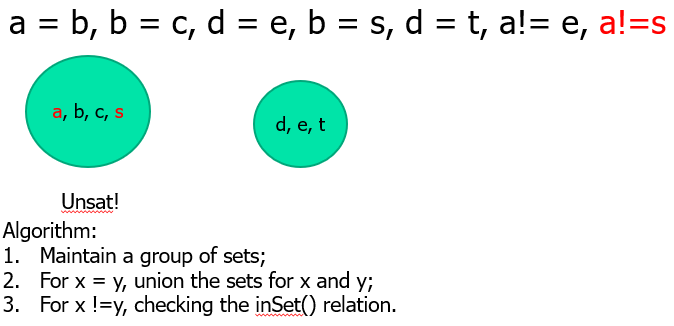
解决未解释函数问题(Uninterpreted functions):
未解释函数通常指一个公式中没有被解释的函数,或者说没有被定义的函数

当函数符号相等,且函数符号接收的参数在对应位置上相等,才称为全等。
EUF 理论的应用
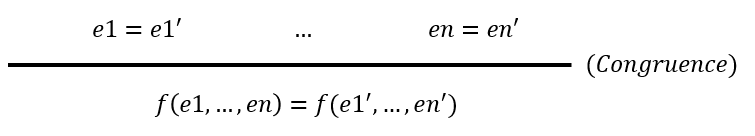
检验代码等价
例1:

例2:

检验命题,实际上就是证明对于任意的相同输入,两者是否产生相同的输出。但由于输入的范围过大,无法构造证明证明,因此只需要证明其反命题是不可满足的即可。
solver.add(Not(F))
线性算术理论 Linear arithmetics
LA 的应用有很多,不仅可以解决一般的线性算术问题,还可以解决:
- 编译器优化
- n 皇后问题
- 子集总和问题
- task scheduling
- task assignment
- 0-1 背包
语法 Syntax

变量论域:
- 在有理数域内(\(Q\)):polynomial(多项式时间)
- 在整型域内(\(Z\)):NPC
问题规模:
- 大规模:Simplex 算法(有理数域 \(Q\)), Branch&Bound 算法(整数域 \(Z\))
- 小规模:Fourier-Motzkin 算法(有理数域 \(Q\)),Omega test 算法(整数域 \(Z\))
Fourier-Motzkin
解决实数论域上的线性算术命题的算法,核心思想就是不断小区变量,得到命题的最终结果
算法流程:
-
等式消除:选择一个等式约束,将要消去的变量用其他变量表示出来,带入到其它约束中
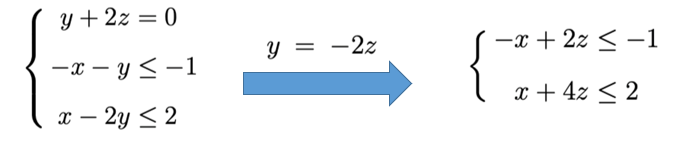
-
无界变量消去:移除包含该变量的所有约束(可能会导致其他变量成为无界变量,这个步骤不断迭代,直到不包含无界变量)
无界变量&有界变量
\(\bigwedge_{i=1}^{m} \sum_{j=1}^{n} a_{i j} * x_{j} \leq b_{i}\)
- 无界变量 \(x_j\) :当变量 \(x_j\) 的系数 \(a_{ij}\)在命题P中全部为正时(有上界),或者全部为负时(有下界)
- 有界变量 \(x_j\) :当变量 \(x_j\) 的系数 \(a_{ij}\) 在命题P中既有正数也有负数时,变量 \(x_j\) 既有上界也有下界
-
正规化 :让所有式子变成 >= 0 的形式
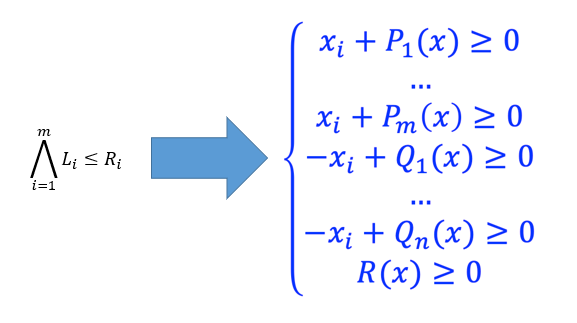
-
找到变量,即存在正系数也存在负系数,即为消去候选,然后就可以正系数负系数两两相加消去 \(x_i\)
-
消去化简后继续 (2) 步,此时不包含 \(x_i\)
特殊情况:

算法总结:
- 对于 \(n\) 个变量和 \(m\) 个约束:每一步可能引出 \(m^2/4\) 个不等式(产生关系式数量爆炸),因此总复杂度为 \(m^{2^n}/4^n\)
- 对于较大的 n 和 m,该算法是低效的,但是小规模的问题依然很使用
【例子】
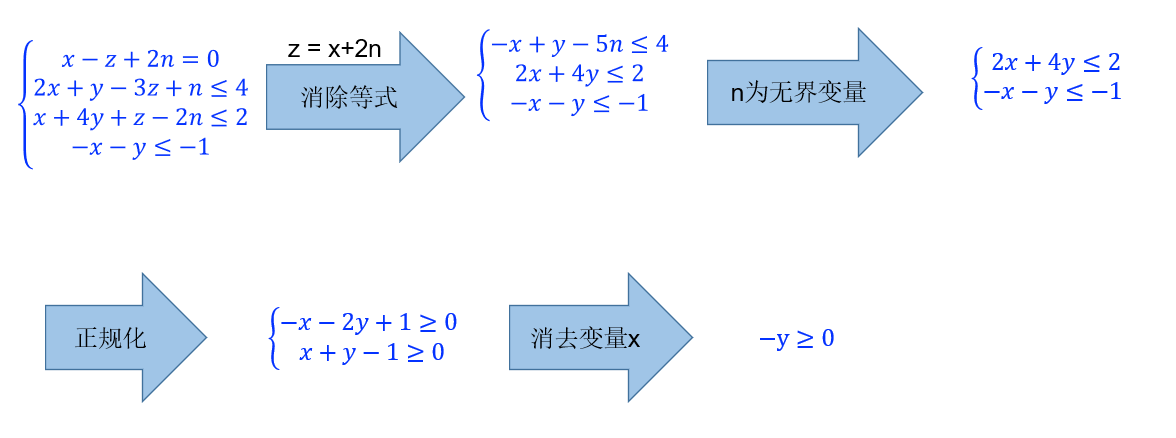
【不太恰当的例子】
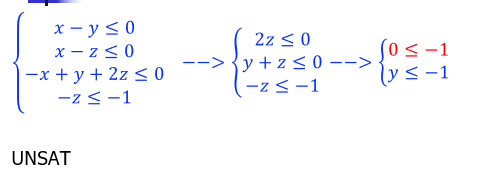
Simplex
线性约束可满足性问题可以转换为几何问题:
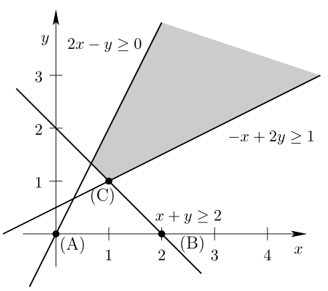
- 每个变量代表一个维度
- 每个约束定义一个凸子空间
- 不等式定义一个半空间
- 等式定义一个超平面
- 解空间由半空间和超平面交集定义,形成一个凸多面体
ps:凸集可以这样描述:用一条直线连接集合里两个元素,这条连线上的所有元素都在这个集合里,这个集合称为凸集
Simplex 算法的几何学意义:
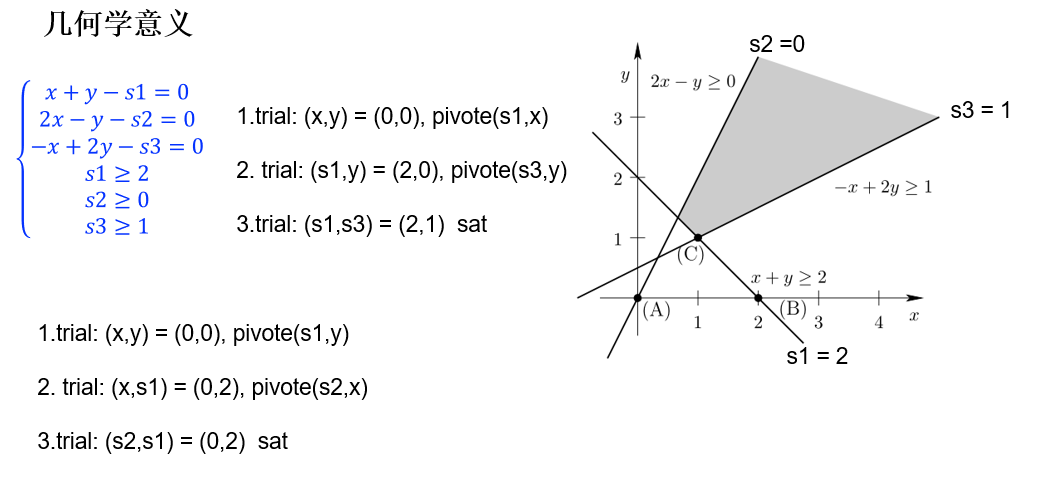
Normal forms: n 个等式+ n 个不等式
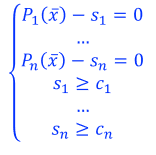
x 称为基本变量(原本存在),s称为附加变量
例如:

Tableau:
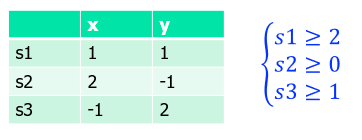
将自变量写在行上,将因变量写在列上,因变量随着自变量的变换而变化,并且因变量可能是对自变量存在约束
问题:是否可以找到x、y使得s1、s2、s3满足约束?
Trail and fix:
给还没确定值的自变量定值为 0 (初始自变量)或边界值(换轴后自变量的 bound),看看是否满足 Tableau 约束,若不满足条件则尝试换轴(pivoting);pivoting 后要满足 Tableau 的约束从而更新 Tableau,然后重复本步骤
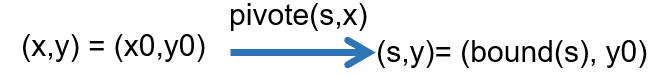
【例子】:
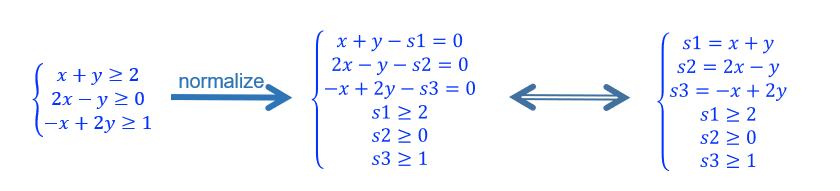



【例子2】:



算法总结:
- 最初用于解决线性规划问题,线性算术的可满足性问题是线性规划的一个子问题
- 最坏情况下的时间复杂度是指数级的
- 可以有效解决含有大量线性约束的线性算术问题
伪代码:
simplex(){
tab = constructTableau();
for(each additional var si){
if(si violates its constraint){
if(there is a suitable xj)
pivot(si, xj);
else return UNSAT;
}
}
return SAT;
}
Branch & Bound(ILP)
主要方法:先当成一个实数域的线性算术问题 \(S\) 去解决:
- 如果不可解,UNSAT!
- 找到一个解 [\(x=r0\), \(y=r1\)]
- 如果 $r0, r1 \in Z $, SAT!
- 添加两个分支(假设仅 \(r0 \in R\) ):
- \(S∪[x ≥ ⌈r0⌉]\)
- \(S∪[x ≤ ⌊r0⌋]\)
伪代码:
branchBound(S){
res = simplex(S);
if(res==UNSAT) // prune
return UNSAT;
if(res are integers)
exit(SAT); // deep return
c0 = select(x of real value);
return branchBound(S ∪[x ≥ ⌈𝑐0⌉])|| // backtrack
branchBound(S ∪[x ≤ ⌊𝑐0⌋]);
}
比特向量理论 Bit-Vectors
语法 Syntax & 语义 Semantics
- Syntax:
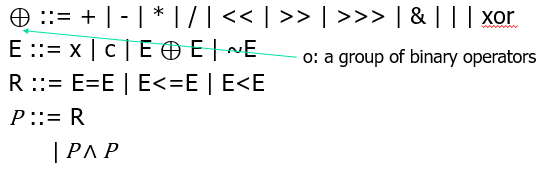
- Semantics:
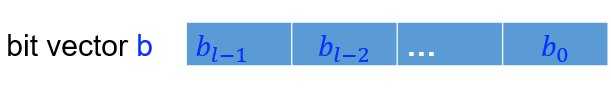

Example:
<11001000>U = 200
<11001000>S = -56 (补码)

x, y = BitVecs(‘x y’, 8)
solve(x+y == 1024)
# why Z3 output:[x=0, y=0] ?
# x,y为长度为8的bitvec,x+y同理,故1024(100,0000,0000)=0(0000,0000)
Bit Blasting
流程:
C = {}; // a set of all generated constraints
// two main passes:
// 1. blast each proposition;
// 2. generate constrains
bitBlast(P){
// convert the proposition to atomic bools
blastProp(P);
// generate constraints
genConsProp(P);
}
- blasting:其实就是给每个可计算出值的节点(即除了 \(\and,=\) 以外的节点)赋予 n 长度的 boolean 数组(bit-vector),以便后面产生约束用
// blastProp() will blast each proposition P
blastProp(P){
if P is (e1=e2){
// for atomic propositions, crawl through
// expressions
blastExp(e1);
blastExp(e2);
}else if P is (P1 ∧ P2){ // trivial recursion
blastProp(P1);
blastProp(P2);
}
}
// genCons() will generate constraints
blastExp(e){
if e is x:
// a vector of boolean variables
return (b0, b1, …, bn);
if e is c:
return (b0, b1, …, bn);
if e is e1+e2:
(b0, …, bn) = blastExp(e1);
(c0, …, cn) = blastExp(e2);
return (d0, …, dn); // attach to e1+e2
// other cases are similar
}
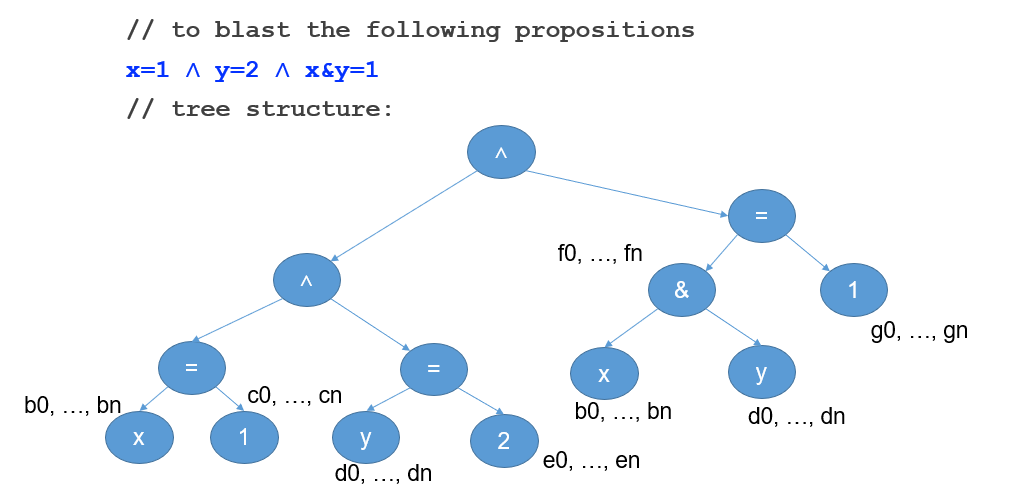
- generating constraints:产生这些 bit-vector 互相之间的约束条件,以便之后扔进 DPLL 计算 SAT
// genConsProp() will generate constraints
genConsProp(P){
if P is (e1=e2):
genConsExp(e1);
genConsExp(e2);
C ∪= {x0=y0, …, xn=yn};
else if P is (P1 ∧ P2):
genConsProp(P1);
genConsProp(P2);
}
// genExp() will generate constraints for exp
genConsExp(e){
switch(e){
case (x&y):
C ∪= {z0=x0 ∧ y0, z1=x1 ∧ y1, …, zn=xn ∧ yn}
break;
case (x|y):
C ∪= {z0=x0 ∨ y0, z1=x1 ∨ y1, …, zn=xn ∨ zn}
break;
case (~x):
C ∪= {z0=~x0, z1=~x1, …, zn=~xn}; break;
case (x+y):
c0=F ∧
r0=xor(x0,y0,c0) ∧ c1=(x0 ∧ y0)\/(xor(x0,y0) ∧ c0)
r1=xor(x1,y1,c1) ∧ c2=(x1 ∧ y1)\/(xor(x1,y1) ∧ c1)
…
case (x-y):genConsExp(x+(-y))
case (x*y):genConsExp(y+y+...+y)
case (x/y):genConsProp(y!=0∧d*y+r=x∧r<y)
}
}
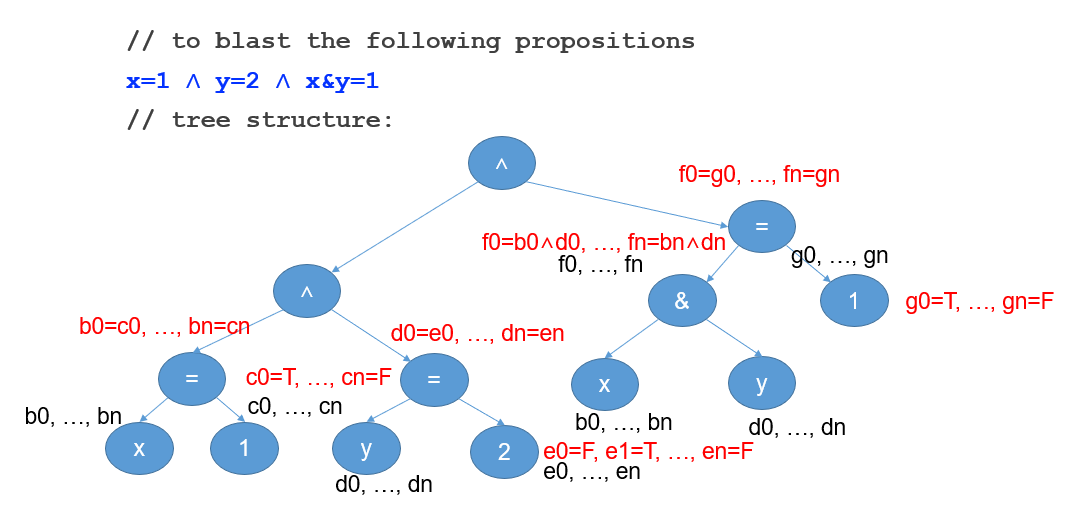
Incremental Bit Blasting 策略:
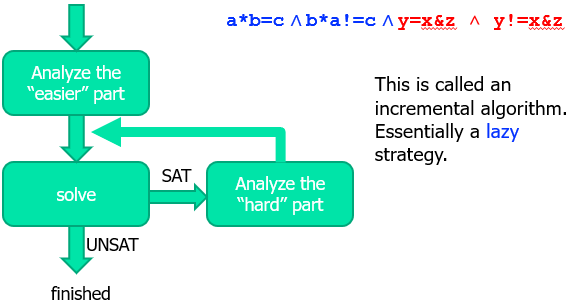
先求解容易求解的部分,如果 UNSAT 直接不满足
Bit-Vectors 的应用
Fermat‘s last theorem(费马大定理):

为什么要 a & magic == 0 ?它让 a、b、c 只能 \(2^4 = 16bit\),在a×a×a的时候会达到48bit<64bit,否则将会溢出!
Question: why we don’t just use integers?Z3不会去遍历所有整数,因为它是无限的,所以要限定范围!
数组理论 Arrays
为什么要研究数组运算?
- 在计算机中,如果有整型向量和array可以推理任何程序
- 数组从接口上看也具有特殊性,数组的读写代表read/write、select/update、look up/insert,代表了符号表查找表一系列结构
语法 Syntax & 语义 Semantics
- Syntax:
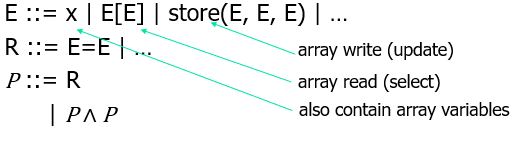
- Semantics:
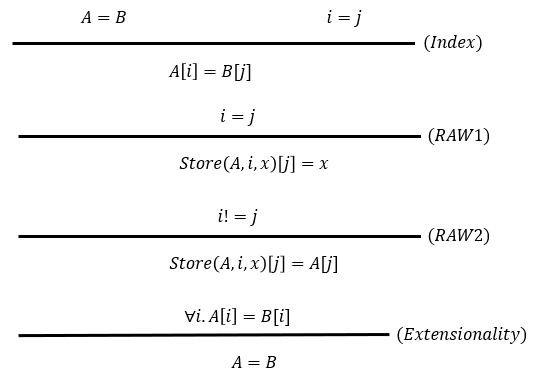
Array Elimination
数组读可以转换成 EUF 理论:

数组写则转换成谓词逻辑:

例如,对于 \(store(A,i,x)[i] >= x\) 会解释为:

restricted array elimination rules:由于数组写转换成的谓词逻辑是不可判定的,我们可以将其限制在某种子集里(出现过的变量集合)

对于 \(E\) 中下标 \(I\) 做出了限制,防止不可判定
流程:
- 消除 array store
- 消除 \(\exist\) 谓词
- 消除 $ \forall$ 谓词
- 消除 array read
- 以 EUF 理论解决
伪代码:
// Given a proposition in array property form,
// convert it into an equivalent EUF formulae.
// Input: any proposition P
// Output: an EUF proposition
EUF arrayReduction(P){
P1 = eliminate all array write: store(A, i, x);
P2 = replace ∃x.P1(x) with P1(y); // y is fresh
P3 = replace ∀x.P2(x) with P2(i)/\.../\P2(k);
P4 = eliminate array read in P3: A[i];
return P4;
}
【例子】:证明 \((\forall x \in N . x<i \rightarrow A[x]=0) \wedge A^{\prime}=\operatorname{store}(A, i, 0) \rightarrow\left(\forall x \in N . x \leq i \rightarrow A^{\prime}[x]=0\right)\)
证明上式即是证明下式为 UNSAT:
\((\forall x \in N . x<i \rightarrow A[x]=0) \\ \wedge A^{\prime}=\operatorname{store}(A, i, 0) \\ \wedge\left(\exists x \in N . x \leq i \wedge A^{\prime}[x] \neq 0\right)\)
step #1:消除 array store
\((\forall x \in N . x<i\rightarrow A[x]=0) \\ \wedge A^{\prime}[i]=0 \wedge \forall j \neq i . A^{\prime}[j]=A[j] \\ \wedge\left(\exists x \in N . x \leq i \wedge A^{\prime}[x] \neq 0\right)\)
step #2:消除 \(\exist\) (用一个新变量 \(z\in N\))
\((\forall x \in N \cdot x<i \rightarrow A[x]=0) \\ \wedge A^{\prime}[i]=0 \wedge \forall j \neq i . A^{\prime}[j]=A[j] \\ \wedge z \leq i \wedge A^{\prime}[z] \neq 0\)
step #3:消除 \(\forall\) (index: \(\{i, z\}\))
\((i<i \rightarrow A[i]=0) \wedge(z<i \rightarrow A[z]=0) \\ \wedge A^{\prime}[i]=0 \wedge\left(i \neq i \rightarrow A^{\prime}[i]=A[i]\right) \wedge\left(z \neq i \rightarrow A^{\prime}[z]=A[z]\right) \\ \wedge z \leq i \wedge A^{\prime}[z] \neq 0\)
简化为
\((z<i \rightarrow A[z]=0) \\ \wedge A^{\prime}[i]=0 \wedge\left(z \neq i \rightarrow A^{\prime}[z]=A[z]\right) \\ \wedge z \leq i \wedge A^{\prime}[z] \neq 0\)
step #4:消除 array read
\(\left(z<i \rightarrow F_{A}(z)=0\right) \\ \wedge F_{A^{\prime}}(i)=0 \wedge\left(z \neq i \rightarrow F_{A^{\prime}}(z)=F_{A}(z)\right)\\ \wedge z \leq i \wedge F_{A^{\prime}}(z) \neq 0\)
很容易证明上述式子是 UNSAT 的,因此原命题是 valid 的
指针理论 Pointer
假设有原始内存模型(即全部值存进内存,而不包含寄存器):
- 内存中存储整型
- 内存地址也用整型表示
- S: x→a表示将变量 x 映射到地址a
- H: a→v表示将地址 a 映射到值v
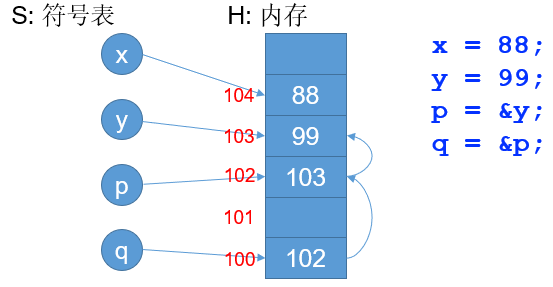
我们希望以下指针语法是 SAT 的:
\(p=\&a ∧ a=1 → *p=1\)
语法 Syntax & 语义 Semantics
- Syntax:
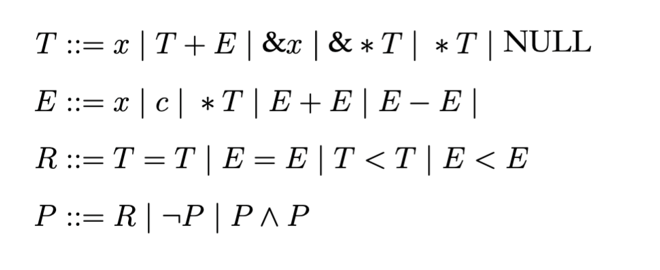
- Semantics:
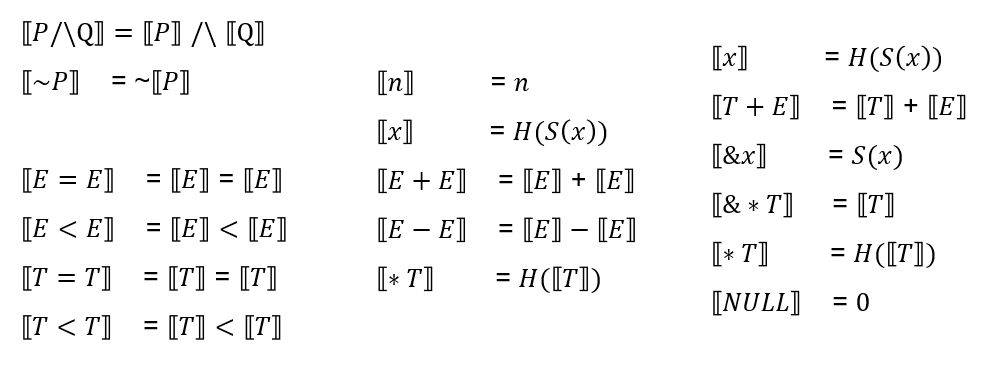
其中 H,S 并没有明确的定义,就可以转换成未解释函数 EUF 问题
【例子1】

【例子2】
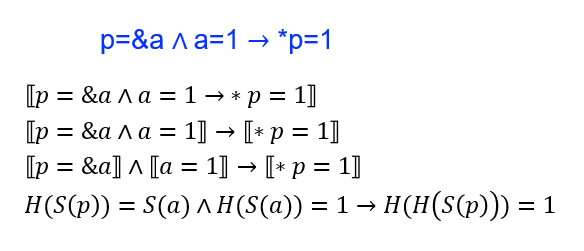
伪代码:
sat(P){
P’ = ⟦P⟧; // Pointer semantics
return sat(P’);
}
内存分区 Memory Partitions
如果一个变量 \(x\) 没有被 \(\& x\) 提取过地址,那么这个变量 \(x\) 称为 纯变量(pure);否则, 变量 \(x\) 被称为 逃逸变量(escaped)。
为了不让纯变量 \(x\) 在指针理论语义计算中也套上一层 \(H(S(x))\)(会导致更大的无谓计算量),可以引入一种新的内存模型 \(R(x)\)
相较于上文的原始内存模型,这种进一步划分内存的思想:
- 相当于额外添加了寄存器,有一个更细粒度的内存模型
- 可以根据内存类型,推断出更多巧妙的属性
【例题】\(*p=1\and**q=1\to p \neq q\)

理论组合 Theory Combination
从本质上来说,一阶逻辑是不可判定的,没有算法对他任意命题的求解,所以便选取一阶逻辑的子集,对子集进行求解,子集即理论。
在这个子集中能表达计算机的一些问题,而且可以找到一些计算机算法能够对子集有效地求解。并且其解释的确定的,即给定一个语法,可以解释到具体的规则上。

理论组合从本质上分为两大类:
- 把每一个理论都分别转换为命题逻辑的公式,然后直接用 SAT 方法求解
- 每个理论分别用其特有的算法进行求解,在求解的过程中两边进行协作,信息互相传播,最终达到稳定状态即解
Nelson-Oppen 算法
理论组合问题,一般来说是不可判定的(即使其中的理论都是可判定的),为了让它变得可判定的,就需要满足以下条件:
- 各自的理论 \(T1\) ,\(T2\) 都是可解的
-
\[\Sigma 1 \cap \Sigma 2=\phi$$ 相交的语法为空(等号 $=$ 除外) \]
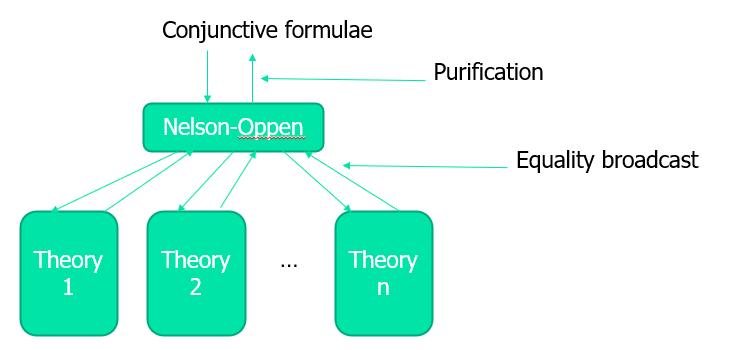
命题可能是混合在一块的
- 纯化(purification):让命题变成满足 \(P_1 ∧ P_2 ∧... ∧ P_n\) 的形式,且每个命题 \(P_i\) 只属于一种理论,并通过变量将不同理论的命题连接起来

- 等式传播(equality propagation):将每个理论分别丢进求解器中,然后返回等式结果,然后经过等式的传播不停反复一直到求解结束

【例题】

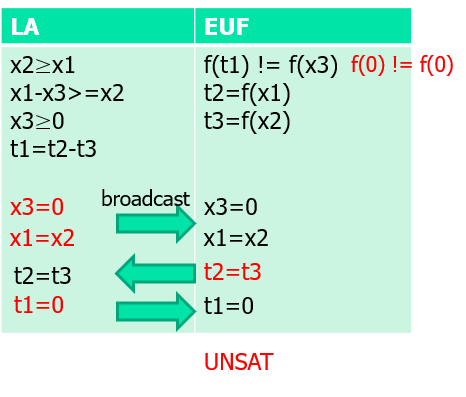

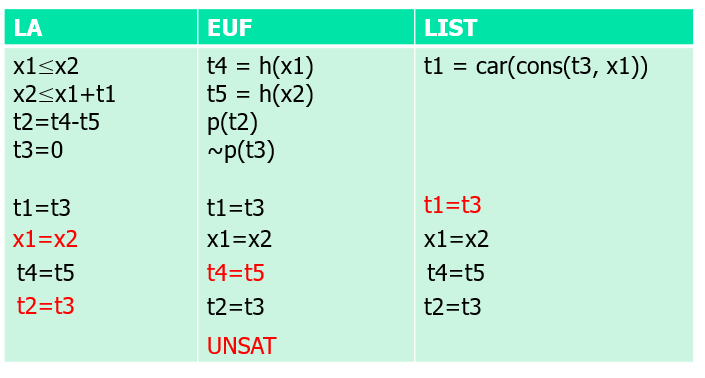
伪代码:
nelson_oppen(P){
P1 ∧... ∧ Pn = purify(P);
L:
if(some Pi is UNSAT)
return UNSAT;
if(some Pi implies x=y){
broadcast(x=y);
goto L;
}
if(Pi implies x1=y1 ∨ … ∨ xn=yn)
nelson_oppen(P, xi=yi);
return SAT;
}
Nelson-Oppen 算法-凸性 Convexity

问题:从上面的例子中可以看出,纯化后并没有等式,在 LA 和 EUF 中无法进行传播,故无法求解
凸理论:如果命题 P 能推出一个析取的等式,P 一定能推出其中某一个
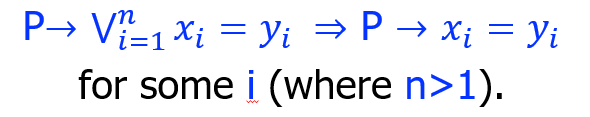
如果理论 \(T\) 叫非凸性(non-convex),那么就不能满足上面的条件
因此需要对 Nelson-Oppen 改进:
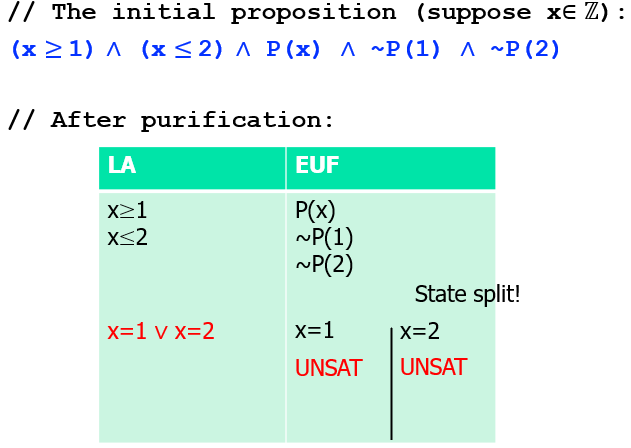
在纯化后得到 x=1 或 x=2 之后需要进行状态分裂(split),将其中一个命题广播到 x=1,另一个 x=2,然后分别对 EUF 求解
伪代码:
nelson_oppen(P){
P1 ∧... ∧ Pn = purify(P);
L:
if(some Pi is UNSAT)
return UNSAT;
if(some Pi implies x=y){
broadcast(x=y);
goto L;
}
if(Pi implies x1=y1 ∨ … ∨ xn=yn)
nelson_oppen(P, xi=yi);
return SAT;
}
Soundness and completeness:
- 对于完备性,即如果 nelson 返回为 SAT 则一定是满足的
- 当返回 UNSAT 时,是不可满足的,但是这种情况很难证明,因为我们不知道传播是否充足(也可能是求解器不行)
DPLL(T) 算法
T 表示 theory,本质上还是要研究 DPLL 算法,即 SAT 算法,但这个算法是以理论 T 作为参数。
类比为在写 C++ 时的泛型或模板算法
用 Nelson 算法研究一个 SAT 问题,要求必须是一个合取式。但是实际上都是各种一般形式,这时候就需要通过 DPLL(T) 求解。
\(一阶逻辑\to抽象\to命题逻辑\to传给DPLL\to聚象\to Nelson\)
抽象前后的可满足性结果可能不同,因为信息量减少!
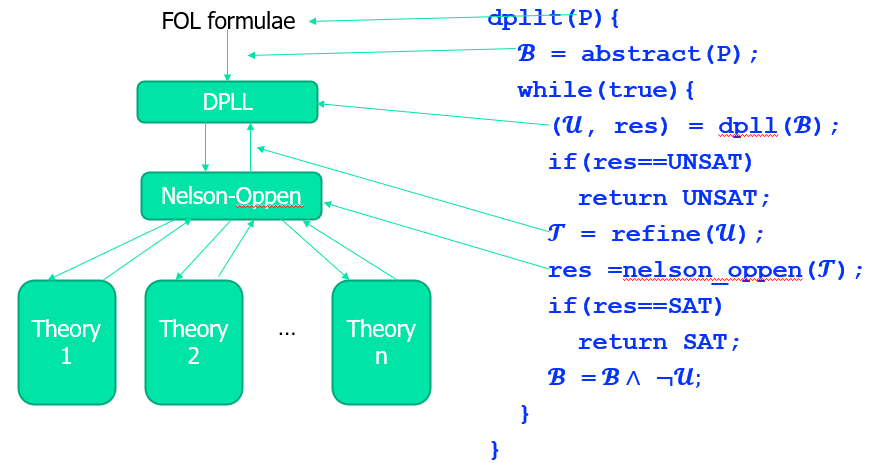
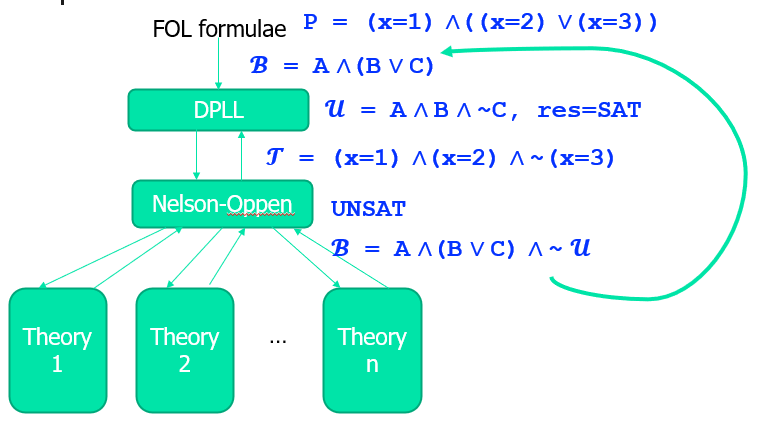
这种解法一般称为离线的,主要特点是把 SAT solver用成一个黑盒,每调用一次都可以得到一个值。
注意:当 Nelson 验证并不成立时,应当把该次 DPLL 计算的 u 完全取否后加入到下一次 DPLL 验证中;例如此次只是证明了如果B成立的条件下C不成立,但是并不能说明C本身不成立
【例题】
- 先将一阶逻辑抽象成各种命题 \(A,B,C,D\),得到 \(B = A\and B\and (C\or D)\),并通过 DPLL 求解器算出一种解 \(u = A \and B \and C \and D\),并向下传播给 Nelson-Oppen
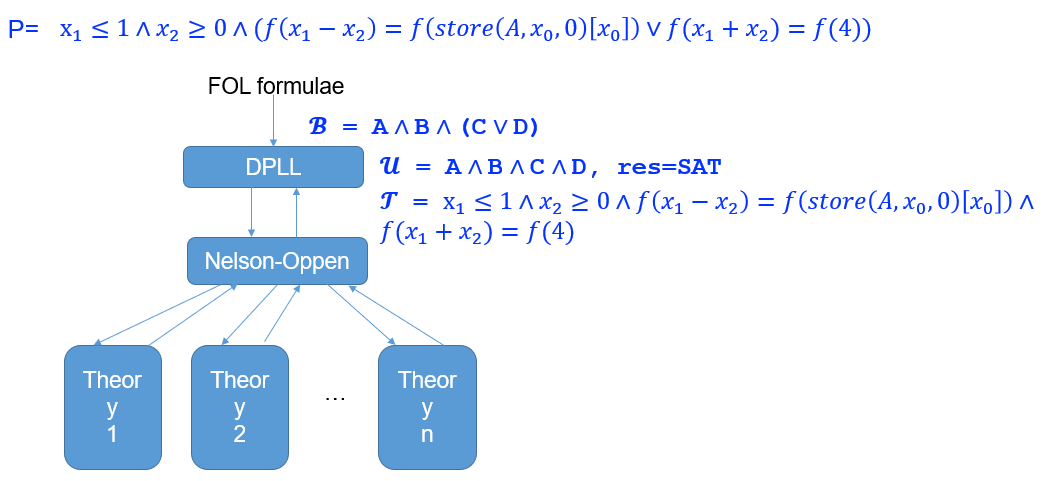
- Nelson-Oppen 算法求解后,发现传来的命题约束有矛盾
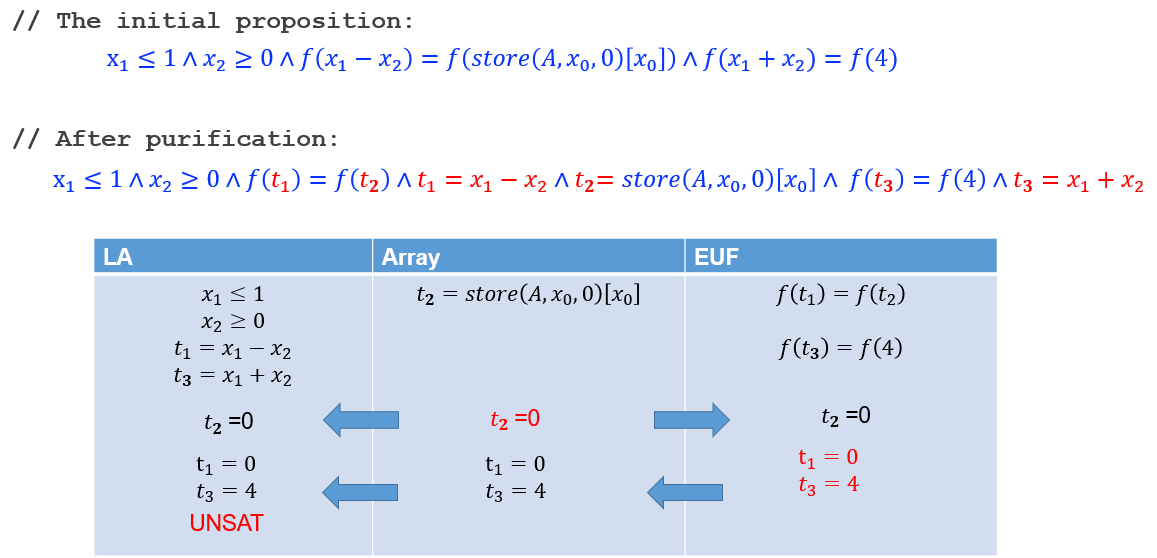
- Nelson-Oppen 向上给 DPLL 报告该解不可行,于是以 \(\and \sim u\) 的形式添加到 DPLL 求解器
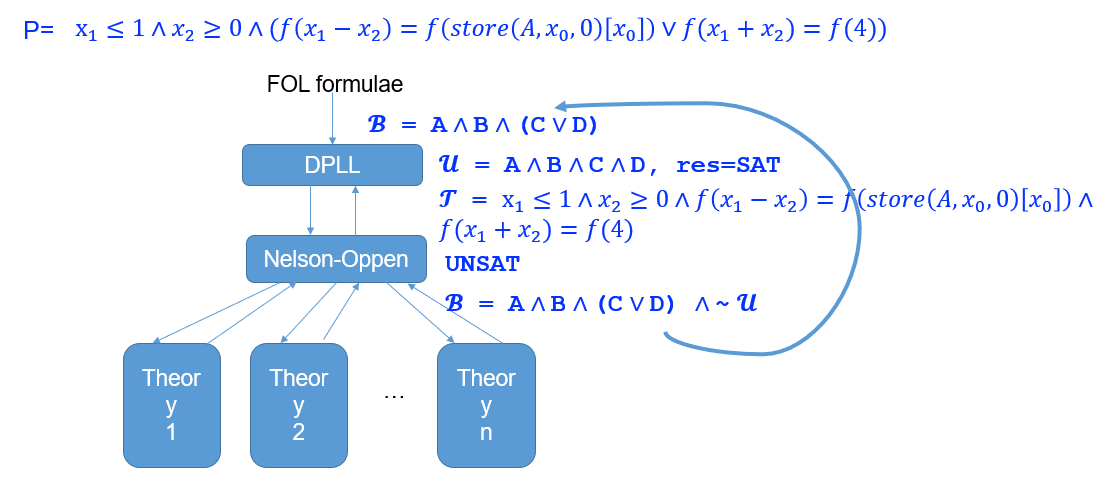
- DPLL 求解器再一次算出一种解 \(u = A \and B \and C \and \sim D\),并向下传播给 Nelson-Oppen
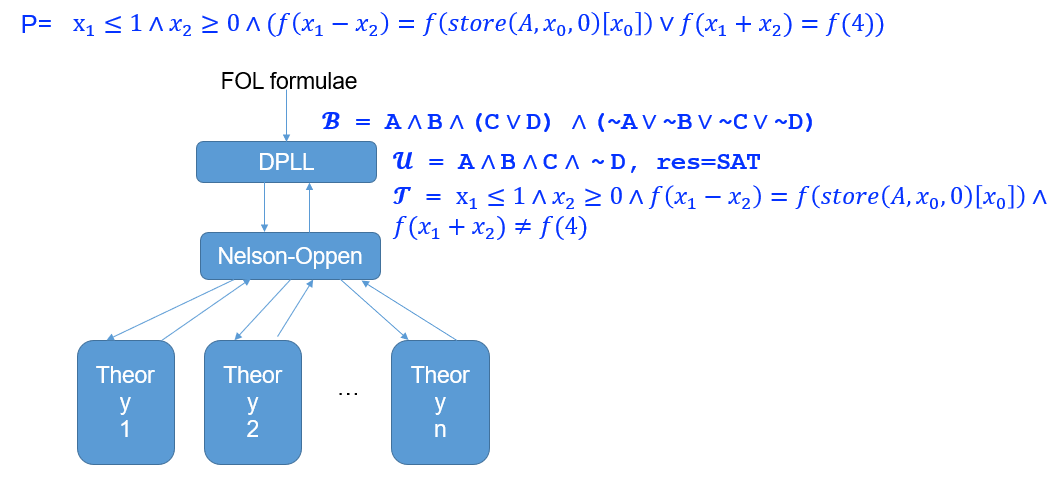
- Nelson-Oppen 求解后,发现可满足,证明为 SAT

操作语义(具体执行) Operational semantics
操作语义:实际上就是把一堆程序语句引入推导规则,从而实现执行程序的效果
在每一步中,\(𝜌⊢S→S’;𝜌’\)
因为在执行 S 之后,S 必然发生了变换,其中可能会存在赋值,导致上下文(存储器) 𝜌 也发生更新
因此,操作语义也被称为解释器,是虚拟机的主要 idea;个人理解的话,更应该称之为具体执行(Concrete execution )

Store:\(𝜌:𝑥→𝑛\)
-
存储器 \(𝜌\) 把变量映射到他们对应的值
-
更新操作: \(𝜌[𝑥↦𝑛]\)
-
读取操作: \(𝜌(𝑥)\)
Judgment:\(𝜌⊢𝐴→𝐴′\)
- 在存储器 𝜌 下,A 化简为 𝐴′
- 𝜌 即用来存放变量,A为正在研究的某一类语法符号。描述了每一类化简形式。
操作语义风格 Operational semantics styles
Big-step operation semantics:\(𝜌⊢𝐸⟹𝑛\)
- 对表达式的计算是一步到位(例如复合结构,忽略内部结构,一步得到结果)
Small-step operation semantics:\(𝜌⊢𝐸→𝐸′\)
- 和大步结构相反,每次只计算一步
- 在小步结构中,必须要走一步,因此并不存在 0 步,即不存在(E—n)的情况
符号执行 Symbolic execution
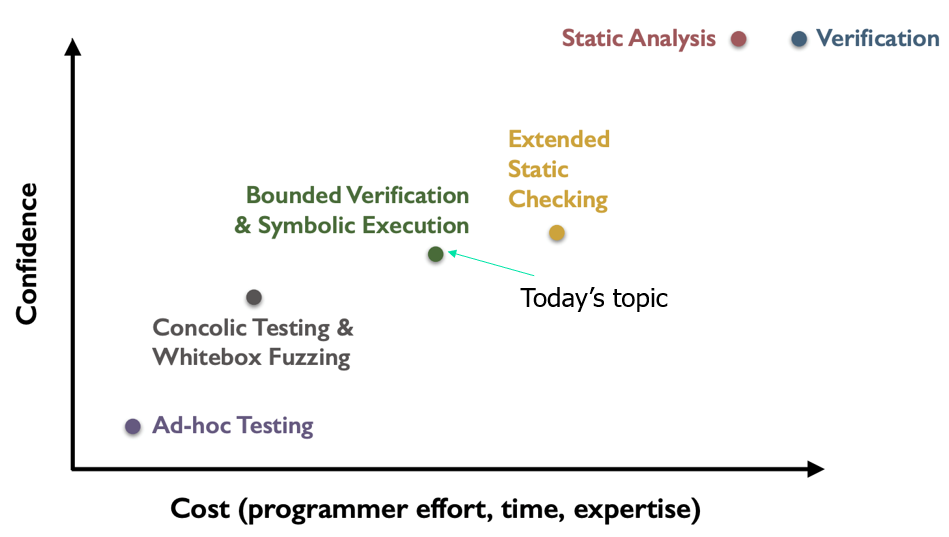
符号执行目的:软件安全领域、软件测试
例如对于以下程序:
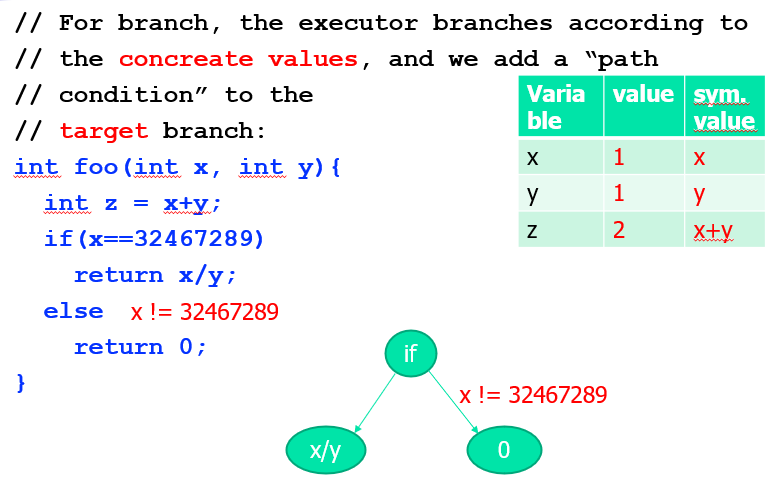
int foo(int x, int y){ if(x==32467289) return x/y; else return 0; }我们希望算出程序可能触发 0 除异常的输入:
- 我们当然可以通过遍历输入的值域来产生具体的输入,然后进行程序测试(用具体的输入值来执行程序,其实被称为 具体执行 Concrete execution),但是这样的暴力遍历很明显是计算量巨大的(多个变量的输入组合数量将是爆炸的)。
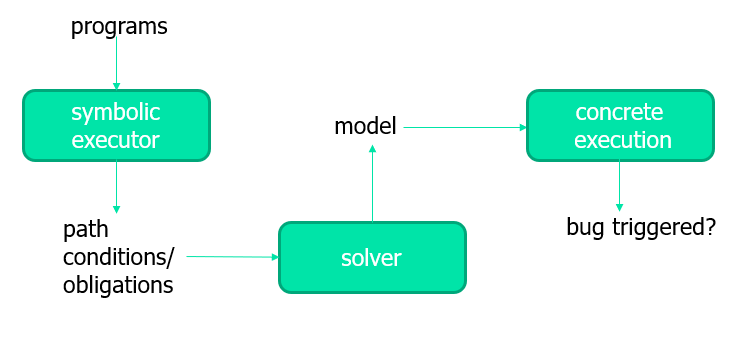
使用符号执行 Symbolic execution 方法,解析程序得到符号约束,最后把这些约束扔进 SMT 求解出具体结果(能导致异常的输入)


【例子1】:
【例子2】:

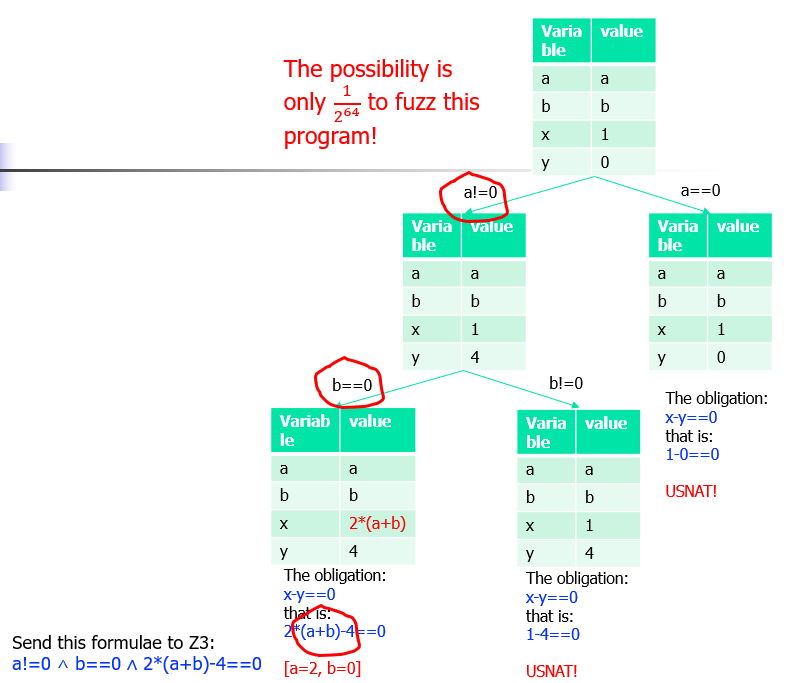
符号执行的实际问题
-
Path explosion:路径爆炸
- 随机选择部分路径,放弃路径的全覆盖
- 根据覆盖信息选择路径
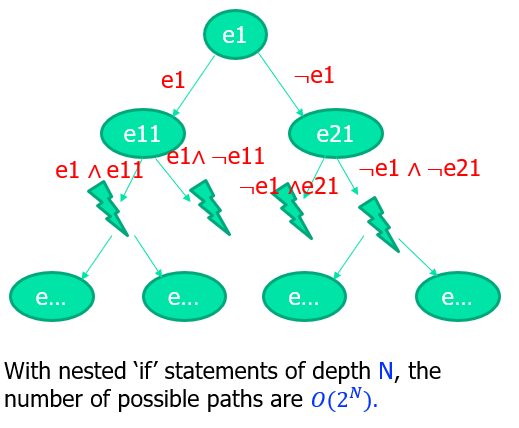
-
Loops and recursions:在符号执行中,符号并不是具体的值,因此循环不会结束
- 解决办法:限制循环次数,其实也相当于限制了路径的全覆盖
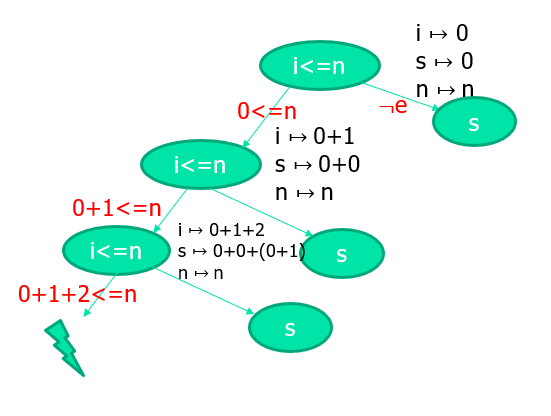
-
Heap modeling:堆栈建模
- 解决方案:建立一个完全的符号堆,太重量级
- 解决方案:利用数组理论和指针理论
-
Environment modeling:符号执行必须对环境进行建模,对所有的库的输入和输出都进行建模
- 结合具体执行(Concrete execution)
- 建立模型:对所有的库的输入和输出都进行建模
-
Constraint solving:
- 约束简化:动态优化约束(像传统编译器优化那样做)
- 求解器缓存和重用(增量式求解)
混合执行 Concolic execution
为了解决符号执行的多个实际问题,可以采用混合的方式,即结合具体执行和符号执行
Concolic = Concrete + symbolic
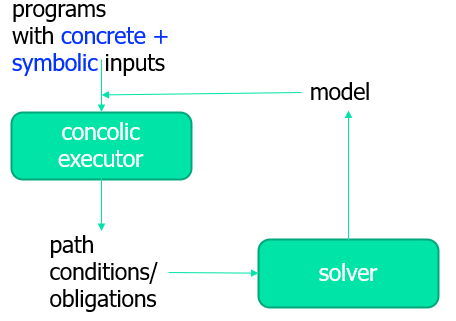
算法流程:
- 对一个待测试的程序,同时生成两种待测试的输入,一组是具体输入(随机取数),另一种是符号数
- 用生成的两种输入运行当前被测试的程序,同时维护两种状态
- 如果有分支语句(条件判断),生成路径条件,但并不像符号执行中生成两种路径条件,并不产生分支。因为可通过具体值来判断哪一种是可行的路径
- 得到路径条件之后,进行取反给求解器,得到其他的具体输入
- 跳到第 2 步重复执行
【例子1】:
【例子2】:

混合执行的优点
- 对于 Path explosion:每次得到一条路径,进行循环,是可控的。但是失去了路径的全覆盖
- 对于 Loops and recursions:混合执行时维护两个状态,是具有具体值的,可以有条件跳出循环而不是限制循环次数
- 对于 Environment modeling:当不知道库函数性质时,直接将具体值带入,没有符号值就将其弱化成具体的数
总之,Concolic execution 是一个更具实践性和更灵活的程序测试方式,但这是牺牲了完备性的基础上换取的实用性
霍尔逻辑 Hoare logic
目的:正确性验证
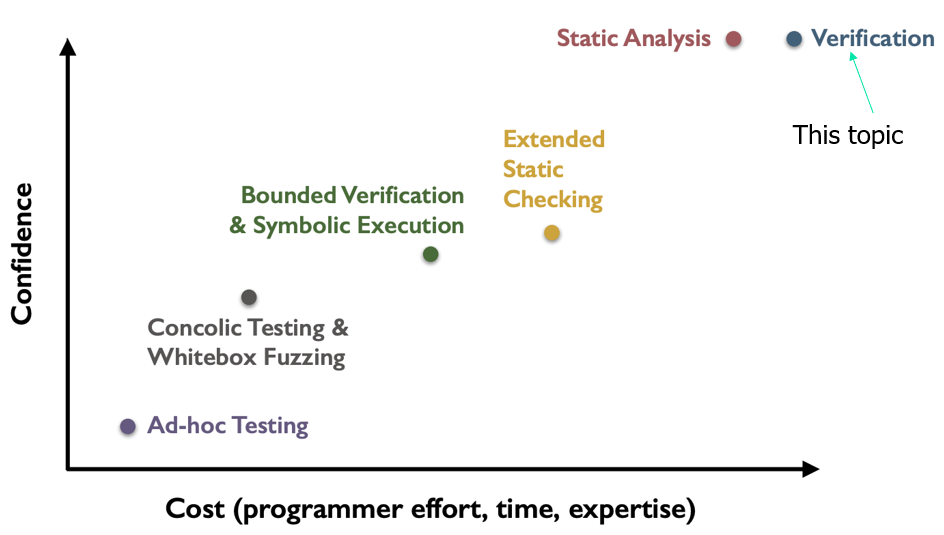
基于霍尔逻辑的正确性验证
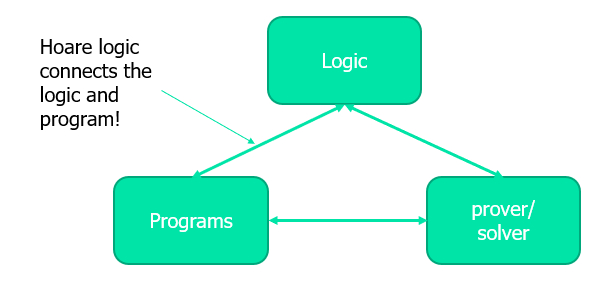
Hoare Triple 霍尔三元组
- {𝑃} 𝑆
其中 P,Q 是两个逻辑命题,前提条件(pre-condition)和后条件(post-condition),S 即程序的语句。
在执行语句S之前,相关变量满足 P 的约束,经过 S 执行中止之后应当满足 Q 的约束;未要求执行是否中止,只是要求了程序的部分正确性。
- [𝑃] 𝑆 [𝑄]
另一种完全正确性,初始状态要满足 P,并且程序 S 一定会终止,然后中止后满足 Q;这被叫做活跃性(liveness)性质。
语法 Syntax & 语义 Semantics
- Syntax:

-
Semantics:
-
\(𝜌⊨𝑃\)
\(𝜌\) 代表存储器(内存),P 在store 𝜌 上成立;也就是说,用存储器 𝜌 上的值取代命题 P 上的变量,结果 P 成立
-
\(∀𝜌.∀𝜌′.(𝜌⊨𝑃 ∧ 𝜌⊢𝑆⟹𝜌′) → 𝜌′⊨𝑄\)
对于任意的 𝜌 在P上成立,并且在 𝜌 下 S 执行得到 𝜌’,依然成立,便可以推出 Q 在 𝜌’ 上成立
-
Axiomatic semantics
定义一套公理系统来做推理。建立一个可靠性和完备性理论:
⊨{𝑃}𝑆{𝑄} ⟺ ⊢{𝑃}𝑆{𝑄}
推导规则:
- empty 空语句,在执行之后状态不变

- assignment 赋值语句 将 P 中的 x 替换成 E

- sequence 顺序(序列)

- if

- while

- consequence (唯一一个不是语法制导)

【例题1】:

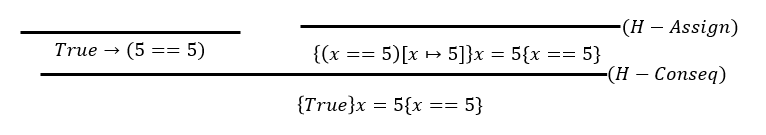
【例题2】:

【例题3】:

自动验证霍尔逻辑
霍尔逻辑的本质是一个推理系统;我们可以基于其定理和推理规则,构造一棵证明树,即使用自动策略来验证霍尔逻辑断言
最弱前提条件 Weakest pre-condition
对于一个霍尔三元组:{𝑃} 𝑆 {𝑄}
给定一个执行 S,通过条件 Q 来计算一个 A,执行 S 后假设 A 满足 Q
那么只需要证明对于任意的 P,𝑃→𝐴 即可。
那么 A 是一个最弱的前提条件(weakest pre-condition)
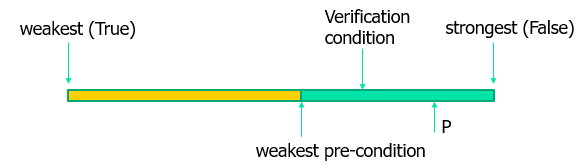

关键问题:对于一个霍尔三元组 {P} S {Q},如何计算最弱前提条件 WP(S, Q)
通过语法制导(syntax-directed)方法,即对执行 S 的归纳来计算一个最弱前提条件生成。
-
empty
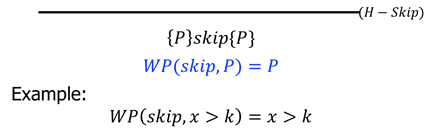
-
assignment
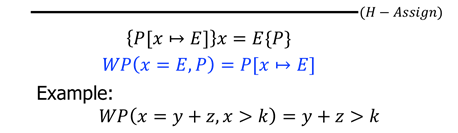
-
sequence

-
if

-
while

【例子1】:

【例子2】:

VC,Verification Condition
最弱前提条件的计算在实际中通常是不可行的,因为可能有无穷的计算,为了让计算变得更加有可行性,可采用 Verification condition 算法
我们希望 VC 可以有两个好的性质:
- 验证条件比最弱前提条件更容易求解
- 比用户给定的前提条件更弱
关键问题:对于一个霍尔三元组 {P} S {Q},如何计算 VC(S, Q)
最核心的洞察就是循环,循环不中止!每写一个循环都要标识一个循环不变式。
\({while}_I(E;S), I\) 就是循环不变式!一般不要求,但是要让循环可行的话就需要给出循环不变式。

有了循环不变式之后就可以构造一个验证条件生成器:

最核心的部分就是生成器算法:


【例子1】:

【例子2】:

【例子3】:

VC 爆炸问题
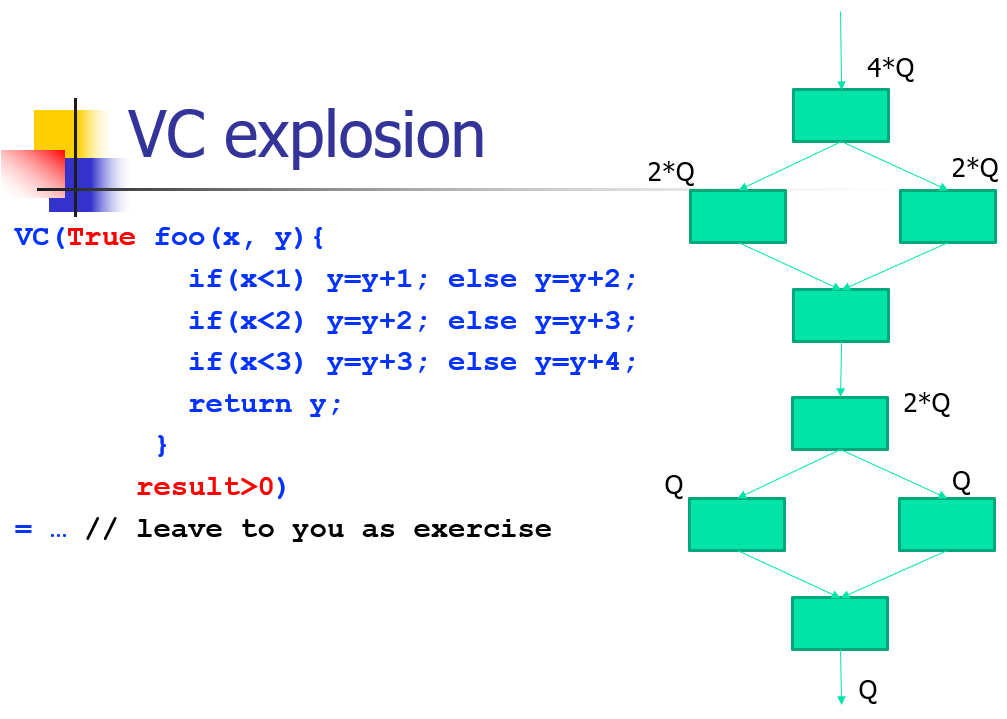
对一个问题分析:
- 可能不存在算法
- 存在算法,但复杂度很高
- 需要存储量较大(VC爆炸)
Forward Calculation of VC
核心思想:使用符号执行(symbolic execution)
- Syntax:

- Semantics:
- 先提前编译程序,将 if 和 while 语句转换成 label 和 goto 形式


【例子】

- 定义符号机器状态:\((pc,ρ,Σ)\),并根据改进的 VC 规则
- \(pc\) 是程序计数器,指向下一个要执行的指令
- \(ρ\) 是符号存储,将变量映射到符号值
- \(Σ\) 是一个不变集合

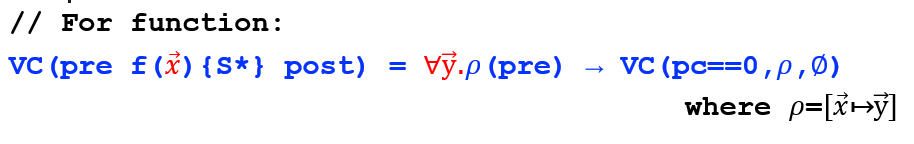
【例子】:
作者:KillerAery
出处:http://www.cnblogs.com/KillerAery/
本文版权归作者和博客园共有,未经作者同意不可擅自转载,否则保留追究法律责任的权利。


























 浙公网安备 33010602011771号
浙公网安备 33010602011771号