USTC 程序语言设计原则笔记 Principle of Programming Language
- 无类型算术表达式 Untyped Arithmetic
- 无类型λ演算 Untyped Lambda Calculus
- De Bruijn 表示法
- 闭包 Closure
- 类型安全理论 Type Safety
- 有类型算术表达式 Typed Arithmetic Expression
- 有类型λ演算 Typed lambda calculus
- Lambda 演算的扩展
- 引用理论 Reference
- 异常理论 Exception
- 子类型理论 Subtyping
- 轻量级Java(FJ)实例分析
- 递归类型 Recursive Types
- 类型重建 Type reconstruction
- 万能类型 Universal Types
- 存在类型 Existential Types
- 类型操作符 Type Operators
- 更高层次多态 Higher-Order Polymorphism
无类型算术表达式 Untyped Arithmetic
一种由自然数和布尔值组成的小型语言,引入抽象语法、归纳定义和证明、求值等基本概念
语法

t 是元变量(非终结符):可以用其他特殊的项(term)来替换的变量,替换后就能得到一个变式,往往记为 \(t'\)
而元变量 \(t\) 及其变式 \(t’\) 均表示对象语言中的项
项的定义
- 归纳定义:

- 推导规则定义:

- 具体定义:

上述方法定义的集合是等价的,即 \(\mathcal{T}=S\)
-
从抽象语法树角度理解项:叶子节点(true、false、0)、中间节点(succ、pred、iszero、if)、树(t)、子树(t1、t2…)
-
项 t 中出现的常量集合 Consts(t):抽象语法树中出现的叶子节点的类型

-
项 t 的长度 size(t):抽象语法树中节点的个数
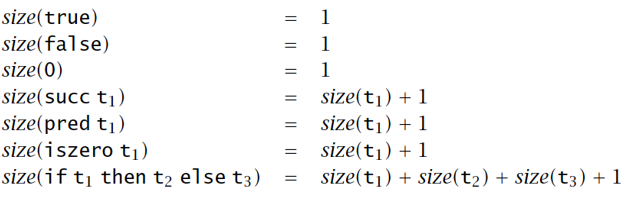
- 项 t 的深度 depth(t):抽象语法树的深度
-
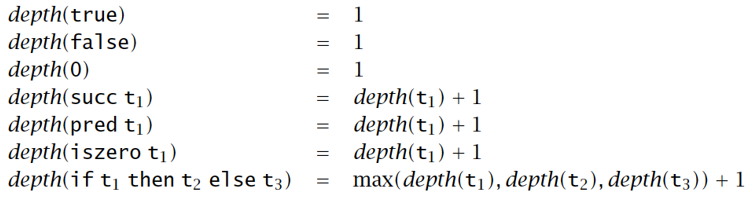
求值语义
操作语义(Operational semantics):通过定义一个简单的抽象机器来说明一个程序语言的行为,把语言的项作为机器的状态,用转换函数定义机器的行为。对于每个状态,要么通过对项做进一步简化给出下一个状态,要么声明机器已经停止。一个项 t 的 语义(semantics) 可以看作是机器在将 t 作为初始状态时达到的最后状态。
而我们希望引入 求值(evaluation) 操作语义,来让这个语言具备求值功能,其实后文还包含 类型(typing) 操作语义,让语言具备类型检查功能。
为了指导这个状态转换,我们引入了求值的推导规则,而推导规则的实质是将处在规则的结论和前提(如果有)相同位置的项来代换每个元变量所得到的结果
\(t → t’\) :根据求值规则,\(t\) 进行一步求值得到 \(t’\)
范式:如果没有求值规则可作用于项 t,则该项是范式(即不存在 \(t’\) 使得 \(t → t’\));每个值都是范式(意味着已经求值到尽头了,已经得到最终结果值了)
Small-step evaluation
小步求值是一种结构操作语义,它的规则可以很方便让机器自动推导求值

if 表达式求值的顺序问题:
- E-If:如果条件 t1 本身是一个条件句(不是值true或false),必须先对 t1 求值
- E-IfTrue、E-IfFalse:当条件 t1 已被求值为true或false时应用
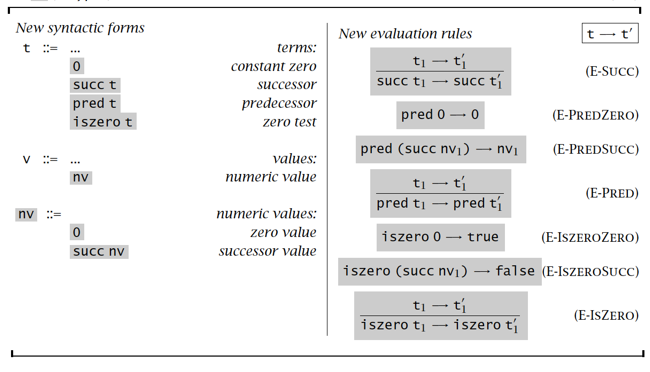
引入新语法形式后:
- t :项(包括值和数值)
- v :值(包括数值)
- nv:数值
【例子】

Big-step evaluation
小步求值的问题:假如遇到例如 Pred true,Succ false,Iszero true 等问题,可能会进入错误的状态,但此时已经完成括号内的大部分求值,浪费了很多计算
大步求值就可以通过删除一些小步规则,更早地发现这种错误状态,但大步求值是一种自然语义,它的规则更适合人手动推导,而不适合机器自动推导(非语法制导)

【例题】改变语言的求值策略使得一个if表达式的then和else分支在条件求值之前被求值。
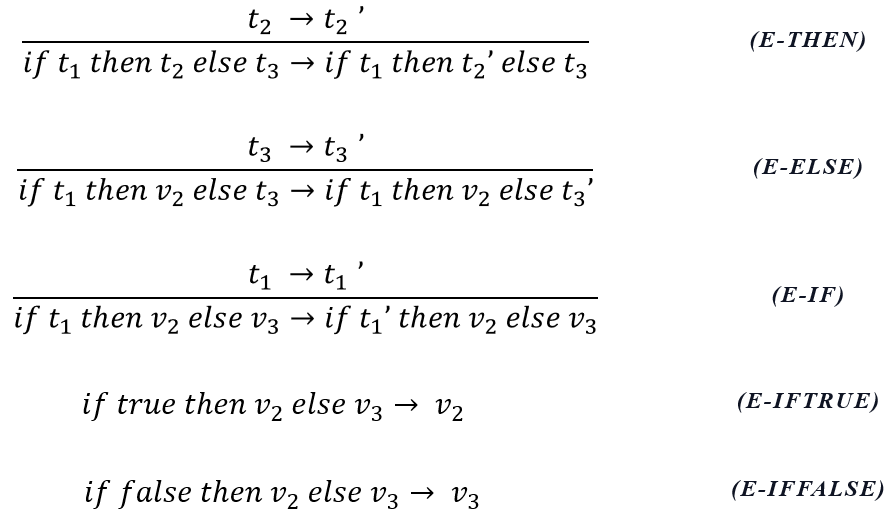
无类型λ演算 Untyped Lambda Calculus
语法

它相当于程序语言中的函数机制,例如:
匿名函数:\(\lambda x.x\)
int f(int x){
return x;
}
嵌套函数:\(\lambda x.\lambda y.x\)
int f(int x){
int g(int y){
return x;
}
}
函数调用:\(\lambda x.\lambda y.x\ \ 2 ==> \lambda y.2\)
int f(int x){
int g(int y){
return x;
}
}
f(2);
恒等函数 \(id=\lambda x.x\)
代换 Substitution
绑定变量 Bind variables:对变量 \(x\),当它出现在抽象 \(\lambda x.t\) 的 \(t\) 中,就说 \(x\) 是被这个抽象所绑定的;实际上绑定变量就是形参
自由变量 Free variables:变量 \(x\) 是自由的,不被任何对 \(x\) 的抽象绑定;实际上自由变量就是全局变量

Substitution 规则,把变量 \(x\) 替换成 \(s\)(常用于实参替换掉形参的操作):
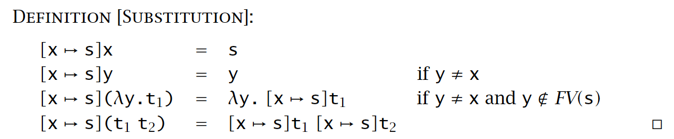
对于 \([x |→ s] (λy.t1)\)
- \(y ≠ x\)(防止把绑定变量换掉)
- alpha 转化:在发现命名冲突如 \(y=x\) 时,重新命名绑定变量,以便代换操作能够正常进行
- alpha 转化示例:\((λx.λy.\ x\ y)\ x\) 等价于 \((λa.λb.a\ b)\ x\)
- \(y ∉FV(s)\) ,确保绑定变量 y 的名称不同于 s 中自由变量的名称(防止代换后绑定变量出现次数变化)
求值语义
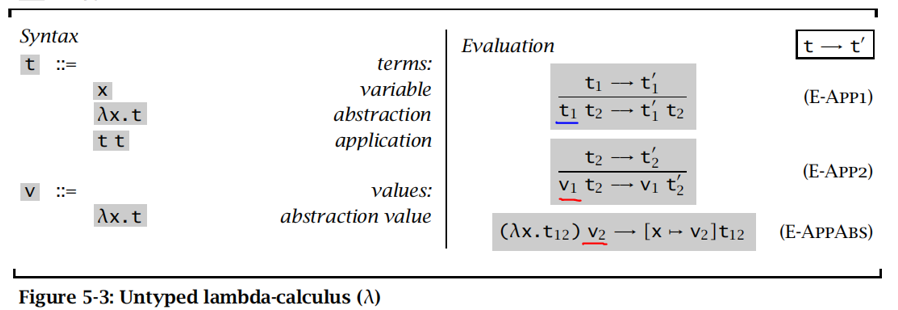
约式:左端部分为抽象的应用(即,形如 的项),称为一个约式(可归约表达式)
beta归约:根据下述规则将右端部分代换为抽象体中的绑定变量,重写一个约式
按值调用策略 call by value
求值顺序问题:确定一个项在下一步求值(归约)中激活哪些约式
- 全 beta 规约:任何时刻可以规约任意位置的约式
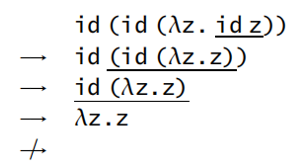
- 规范顺序策略(normal order strategy):最左边、最外面的约式总是第一个被规约
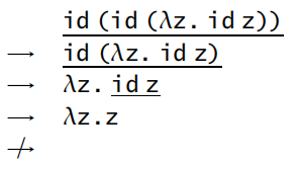
- 按名调用策略(call by name):不允许在抽象内部进行规约

本课程采用的策略是 按值调用策略(call by value):只有最外面的约式可以归约,并且只有当该约式的右边均已归约到一个值时才能进行归约(先规约右边为值得前提下的、最靠外的约式)
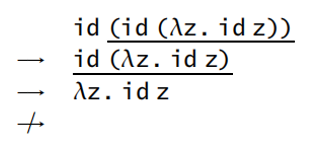
Currying
lambda calculus 没有对多参数提供支持,currying 的思想就是把多参数函数转换为高阶函数达到相同效果
对于多重参数的情况:
- un-curry 形式:例如,\(\lambda(x, y).x\) 和 \((\lambda(x, y).x)\ \ (3, 4)\)
- curry 形式:例如,\(\lambda x. \lambda y. x\) 和 \((\lambda x.\lambda y. x)\ \ 3\ \ 4\)
currying:un-curry 形式转化为 curry 形式
对于括号顺序的约定:
- 应用采用左结合,即 \(s\ t\ u\) 等价于 \((s\ t)\ u\)
- 抽象体采用右扩展,即 \(\lambda x.\lambda y.t\) 等价于 \(\lambda x.(\lambda y.t)\)
【例子】:
- $\lambda x.\lambda y.x\ y\ x $ 等价于 \(\lambda x.(\lambda y.((x\ y)\ x))\)
- \(y\ (λx.x)\) 可省略为 \(y\ λx.x\),但形如 \((λx.x)\ y\) 时不能省略
- \((((t1\ t2)\ t3)\ t4)\) 可省略为 \(t1\ t2\ t3\ t4\)
- \(\lambda x.(t1\ t2\ t3\ t4)\) 可省略为 \(\lambda x.t1\ t2\ t3\ t4\)
【更多例子】:

Lambda calculus 与程序语言
一个 Lambda calculus 的基础模型就可足以表达所有程序语言的特性:
尽管实践中是需要更多语法糖的
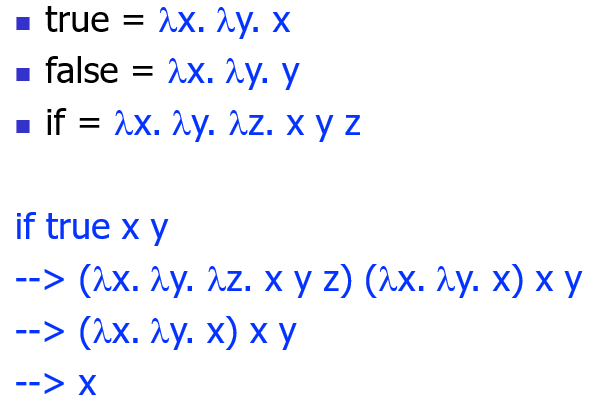



对于数值 n :只需要把 n 次 s 应用到 z ,例如 \(4 = \lambda s.\lambda z.s(s(s(s\ z)))\)
这里 m,n 都是形如数值的形式
【例子】:
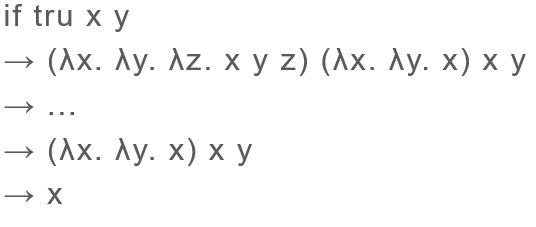

递归问题:
不能求值到一个范式的项称为发散的
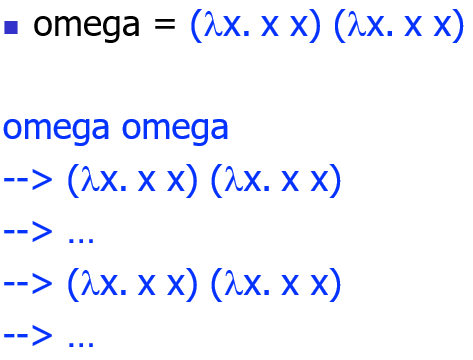
De Bruijn 表示法
由于在 Lambda calculus 中变量名(字符串)的比较太过缓慢,我们可以用 De Bruijin 方法来对参数进行编号

语法

编号 n 意味着它是对应第 n 层 lambda 之外的实参(最里面的一层为 0 层)
【例子】
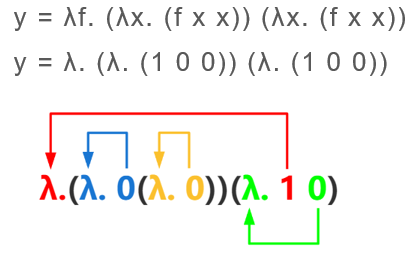
命名上下文:一次对所有自由变量指派一个 de Bruijin 索引,并在需要选择自由变量的数时保持一致地使用这个指派
一般从0逐渐递增,随意指派谁都可以
【例子】
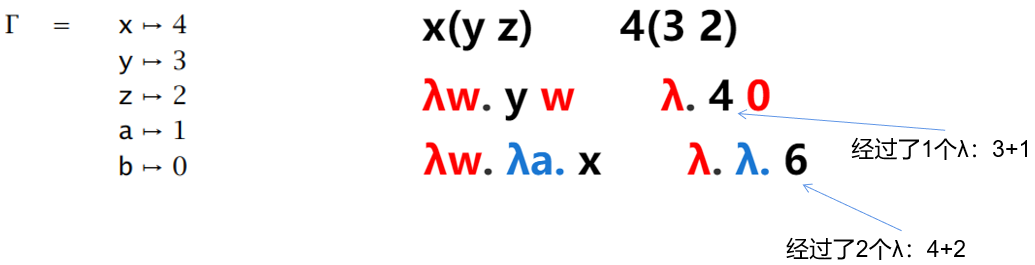
对于 自由变量 free variables 情况:需要填充 fake lambdas,同时对上下文指派对应的 de Bruijin 索引
例如:\(\lambda x. \lambda y .z \ \ x \ \ y\) 存在 \(z\) 是 free variable
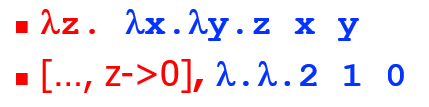
红色部分不应当写出来,只是为了说明填充手段
代换 Substitution
移位:将一个项中的 自由变量 的索引重新编号
一定注意!对绑定变量无任何影响!
移位函数 采用 截参数 c 来控制哪个变量应该移位
- 截参数为 0 时,意味着所有变量都要移位
- 从 0 开始,移位函数每通过一个绑定器,截参数增加 1
一个项 t 在截 c 上的 d 步移位,记为 \(\uparrow_{c}^{d}(\mathrm{t})\)
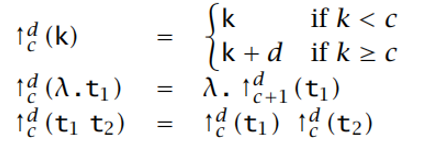
代换 Substituion:

【例子】

求值语义
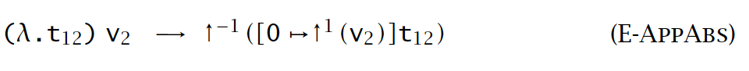
【例子】
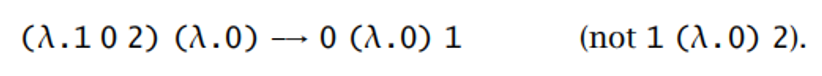
闭包 Closure
lambda calculus 每一次应用 app 规则都要对整个表达式进行遍历来找到要替换的变量。
closure 的思想就是引入一段记录,来记录 free variable 的值,这样应用 app 规则就可以直接查表无需再次遍历整体。
语法 & 求值语义
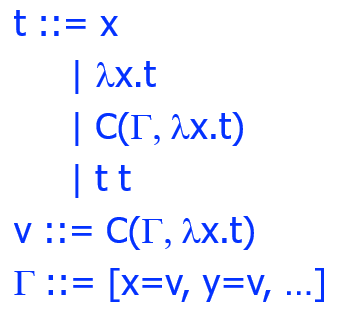

【例子】
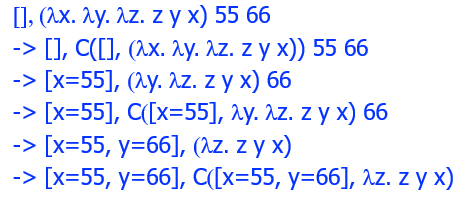
类型安全理论 Type Safety
- Safety = Progress + Preservation
Progress:类型良好的 term 是不会阻塞的(意味着该 term 要么是一个值或者可以继续求值)
Perservation:如果一个类型良好的 term 进行一步求值后产生的 term 也仍然是类型良好的

也就是说在保证 Safety(通过类型检查)后,就可以保证 T1 == T2 == T3 ...
- 为什么引入类型系统?
可通前期过对类型的静态分析和检查,判断一个项(表达式)是否正确,减少进一步对项计算的步骤
有类型算术表达式 Typed Arithmetic Expression
语法 & 类型语义
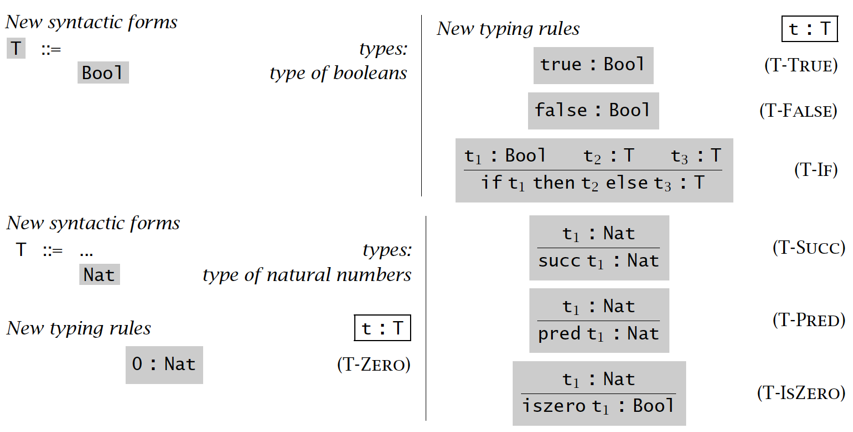

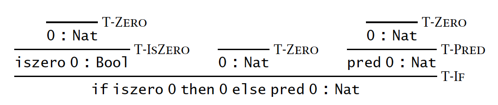
【例子】
有类型λ演算 Typed lambda calculus
类型系统是一种很强的约束,从而带来了 Safety,但如果引入更多高级类型,那么它的 Safety 便会弱化
- 例如对于某些特殊例子,就得引入更高级的类型:\(omega = \lambda x.x \ x\)
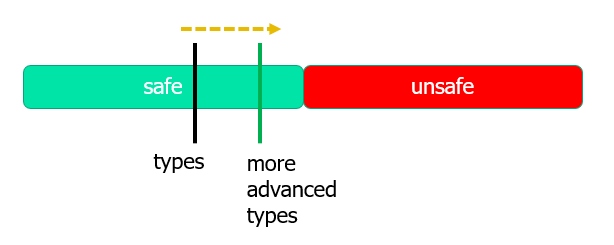
语法 & 求值语义 & 类型语义
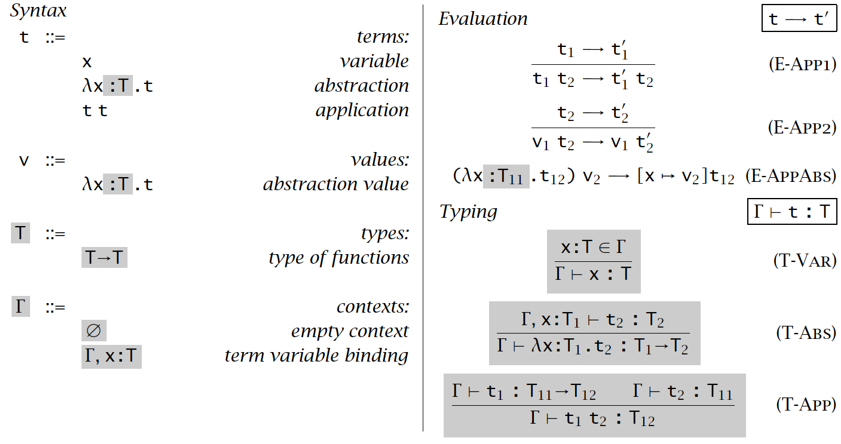
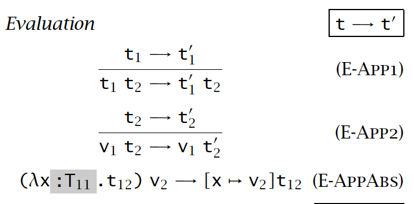


【例子】
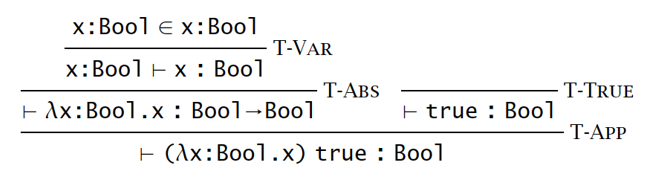
Erasure and Typability
在 evaluation 阶段,类型信息是不需要的。因此编译器可以在类型检查结束后将类型信息消除(erase)掉


Lambda 演算的扩展
lambda calculus 对于理论学习已经足够好用了,但对于实际编程来说是不易用的,因此我们可以在 lambda calculus 的基础上扩展出一些结构形式,实际上被称之为语法糖
Base type
Base type 表示未解释的抽象类型
在 C++ 语言里,其实就是模板类型参数 T

【例子】
lambda x:A. x <fun>: A -> A lambda x:B. x <fun>: B -> B
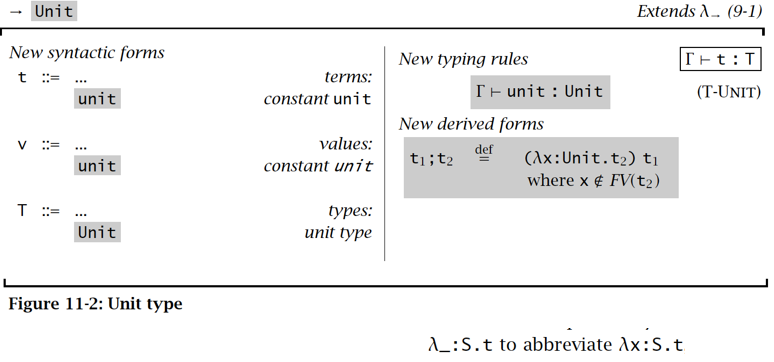
Unit type
Unit type 代表空值
在 C++ 语言里,其实就相当于 void
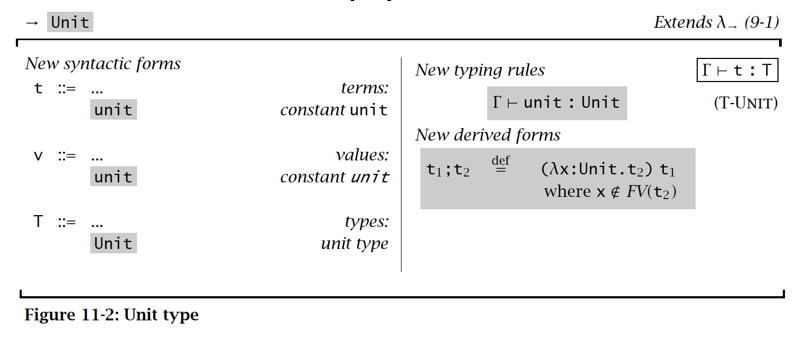
序列&通配符 Sequencing & Wildcard
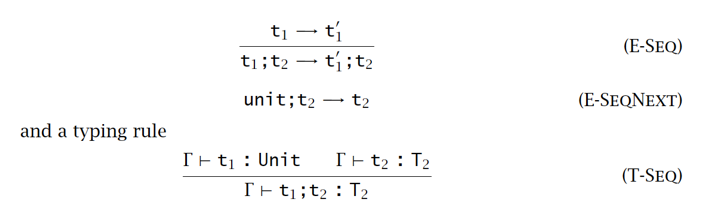
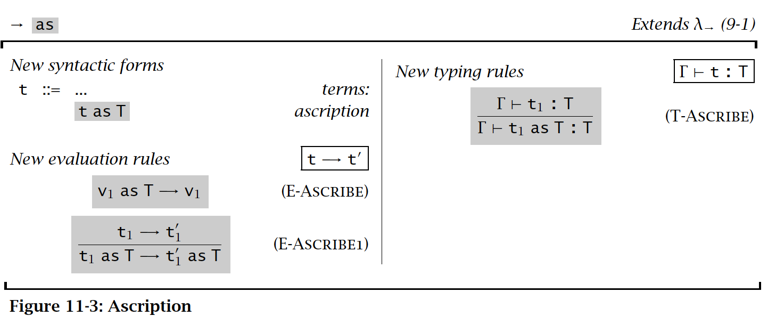
类型标注 Ascription
相当于 C++ 语言里的类型转换
Let Binding
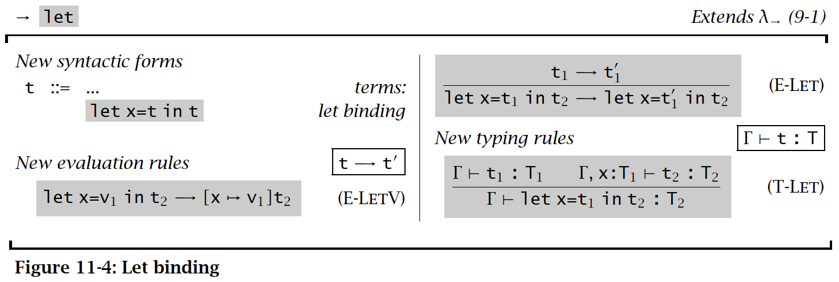
\(let\ \ x=t_{1}\ {in}\ t_{2}\) \(\stackrel{\text { def }}{=}\) \(\left(\lambda x: T_{1} . t_{2}\right) t_{1}\)
二元组 Pair
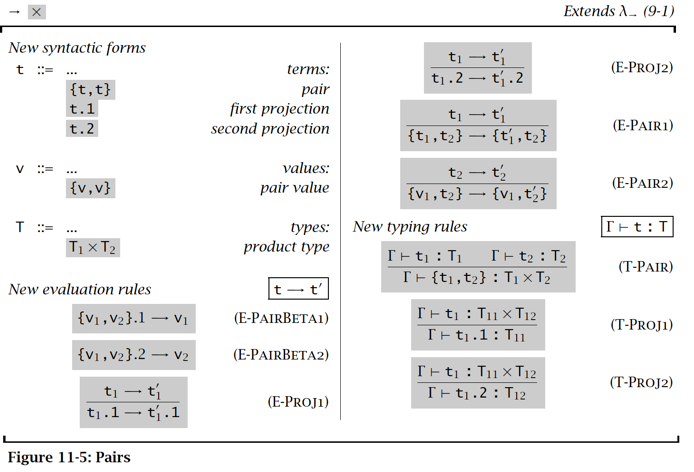
【例子】

n元组 Tuple
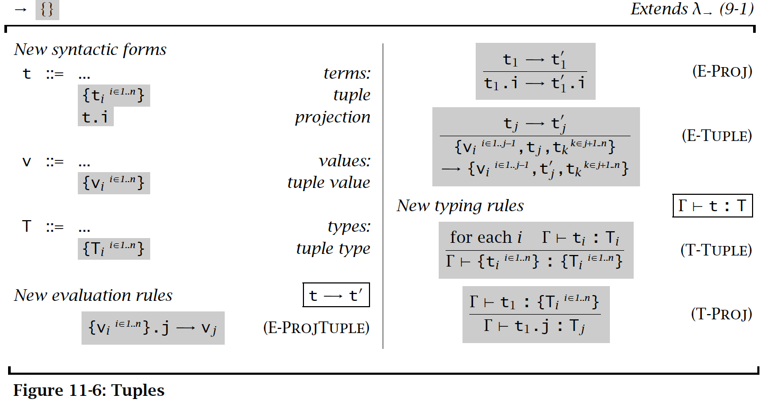
Records
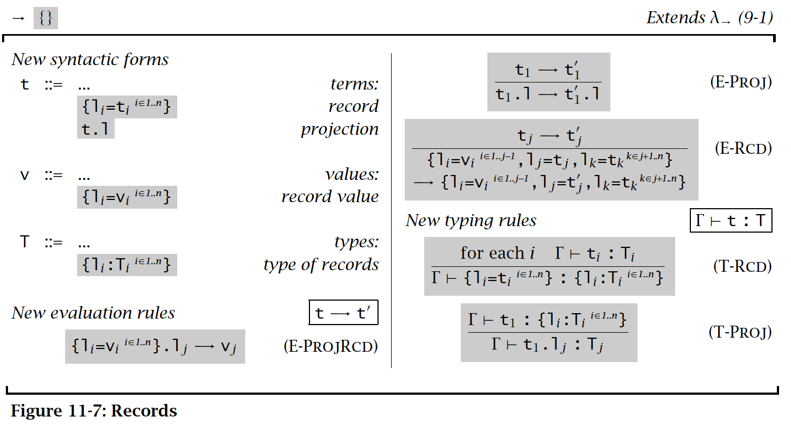
Sum
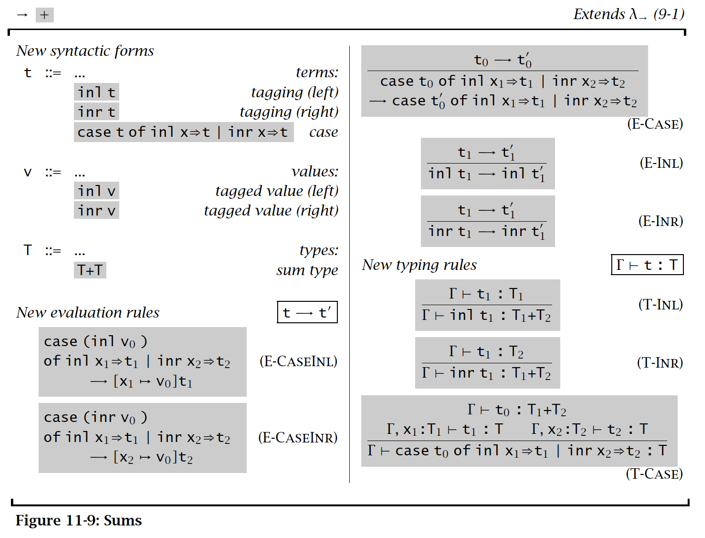
【例子】

Variant
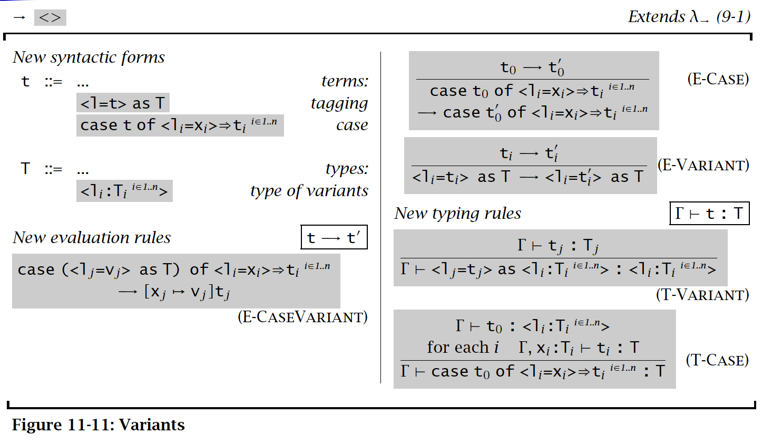
Recursion
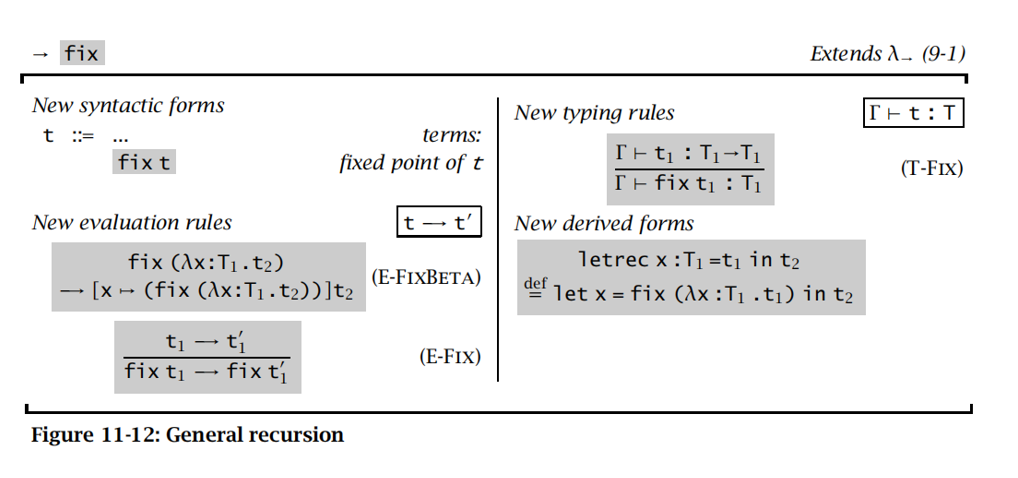
Lists
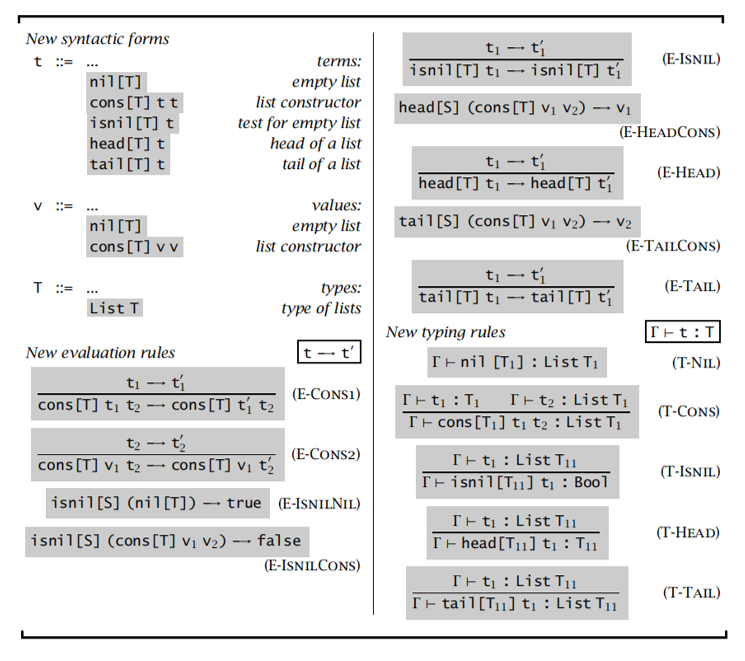
引用理论 Reference
为了引入 Reference 类型,就需要引入一个类型存储;实际上,Reference 是一个纯函数式编程的漏洞
语法 & 求值语义 & 类型语义
Syntax:
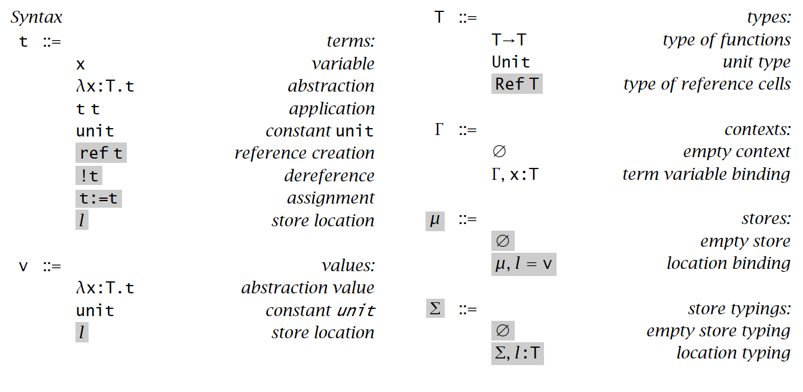
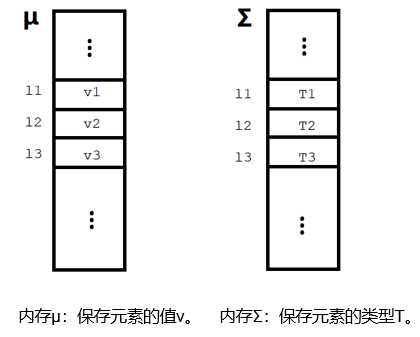
Evaluation semantics:

Typing semantics:
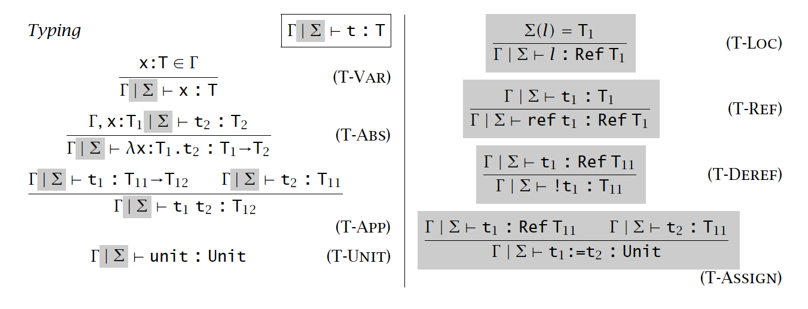
引用类型满足类型 Safety:
-
理论 [Preservation]:如果
\(\Gamma \mid \Sigma \vdash \mathrm{t}: \mathrm{T}\)
\(\Gamma \mid \Sigma \vdash \mu\)
\(\mathrm{t}\left|\mu \longrightarrow \mathrm{t}^{\prime}\right| \mu^{\prime}\)
那么,存在某些 \(\Sigma^{\prime} \supseteq \Sigma\),
\(\Gamma \mid \Sigma^{\prime} \vdash \mathrm{t}^{\prime}: \mathrm{T}\)
\(\Gamma \mid \Sigma^{\prime} \vdash \mu^{\prime} .\)
-
理论 [Progress]:假设 \(t\) 是闭合的,类型良好的 term(也就是说,存在一些 \(T\) 和 \(\Sigma\) 会令 \(\varnothing \mid \Sigma \vdash t:T\))那么不管 \(t\) 是不是一个值,对于任何满足 \(\varnothing \mid \Sigma \vdash \mu\) 的存储器 \(\mu\) ,会存在一些项 \(t'\) 和存储器 \(\mu'\) 满足 \(t \mid \mu \to t' \mid \mu'\)
异常理论 Exception
需要优雅地处理异常事件,如:
- 0 除问题
- 数组越界
- 内存
那么就需要引入一些机制让代码从被调用者全局“跳跃”到调用者:也就是异常机制
异常 Exception

- error 作为无论是函数还是参数的求值结果均为 error
- error 可以是任意类型的
【例子】:

处理异常 Handling exceptions
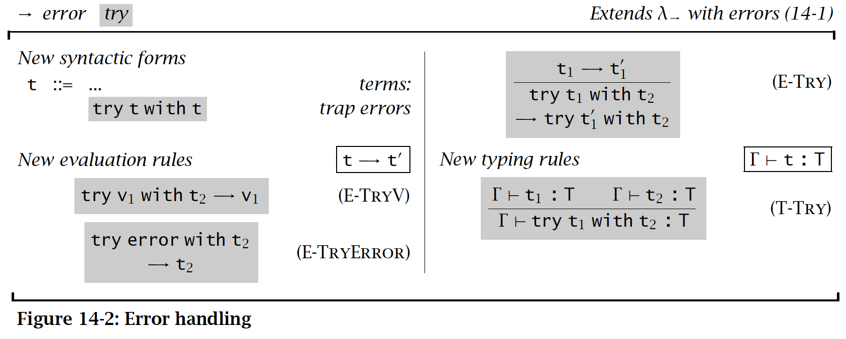
求值规则:try t1 with t2
- t1 能够进一步求值,则求 t1 (E-Try)
- t1 能正确求值 v1 ,则表达式返还 v1,结束
- t1 求值为 error,则求 t2(E-TryError)
含有值的异常 Exceptions carrying values
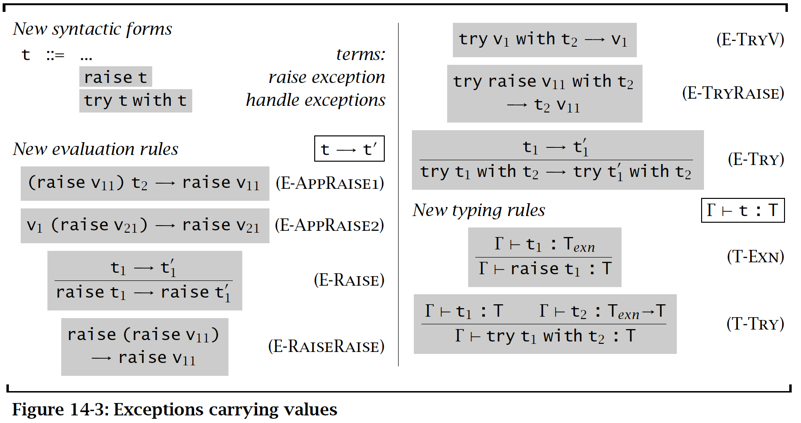
\(T_{exn}\) 可以是任何类型,例如 nat, string, data type, classes ...
子类型理论 Subtyping
目的:实现面向对象语言的基础
总结:
- 声明性子类型:声明和证明属性
- 算法子类型:更高效地实现,语法制导(更进一步可以说是类型制导)
声明性子类型 Subtyping
\(S<:T\)
- \(S\) 是 \(T\) 的子类型
- \(T\) 的元素是 \(S\) 中元素的子集
子类型化规则:
-
包含规则、自反性规则、传递性规则(非语法制导):
自反规则没有前提,传递规则没具体说明 U,且这两个规则中 S 和 T 是裸露的元变量,它们的结论覆盖了其它子类型化规则的结论
包含规则也存在裸露、没有被说明为具体形式的元变量 t ,导致其可以用于任何一项,从而无法确定该使用哪条规则
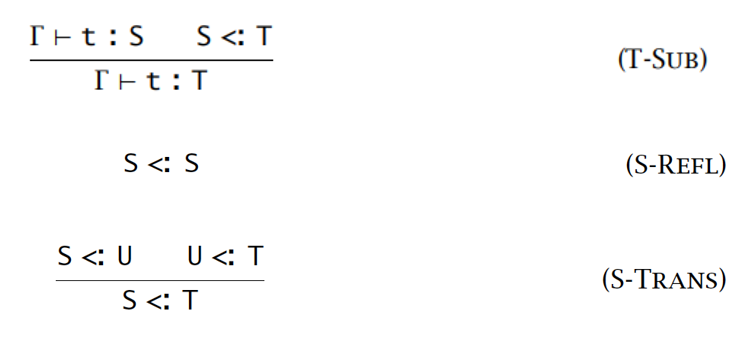
- 广度子类型化:
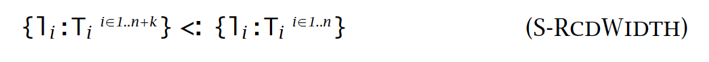
- 深度子类型化:
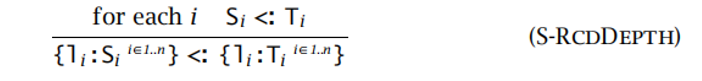
- 记录中字段的顺序发生变化不影响该记录的安全使用(同名字段仍保持子类型关系):
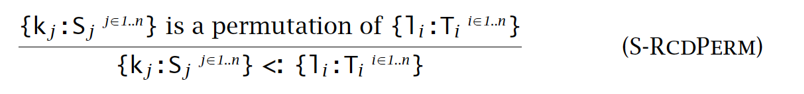
- 函数子类型关系,需满足:
- 子类型函数 \(S\) 所需要的输入信息比父类 \(T\) 少(逆变)
- 子类型函数 \(S\) 所需要的输出信息比父类 \(T\) 多(协变)
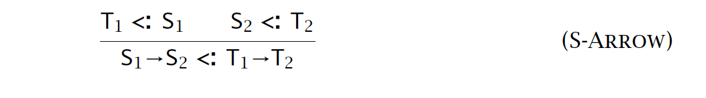
协变:能在使用父类型的场景中改用子类型。如:记录型;变式型;函数型(箭头型)的右端
逆变:能在使用子类型的场景中改用父类型。如:函数型(箭头型)的左端
不变:不能做到以上两点的被称为不变
-
变式类型:协变式
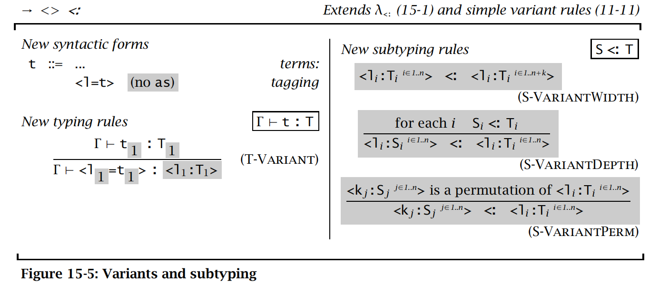
-
列表类型:协变式
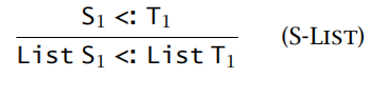
-
引用类型:不变式
为了保证类型的安全,需要:
- 读时要读到不少于上下文要求的类型的信息
- 写时要提供不少于上下文要求的类型的信息
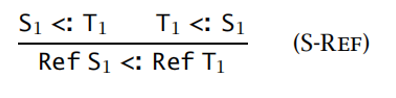
-
数组类型:不变式
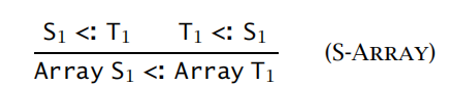
【例子】
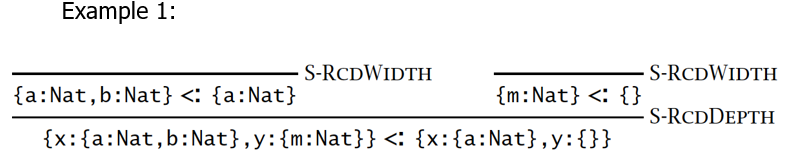
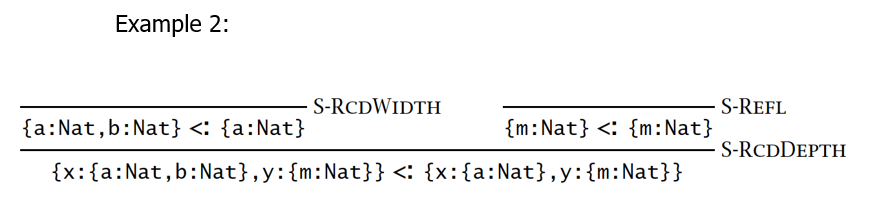

声明性子类型化满足类型 safety:
- 理论[Preservation]:如果 \(\Gamma \vdash \mathrm{t}: \mathrm{T}\) 并且 \(t\to t'\),那么 \(\Gamma \vdash \mathrm{t}^{\prime}: \mathrm{T}\)
- 理论[Progress]:如果 \(t\) 是一个封闭的、类型良好的项,那么 \(t\) 要么是一个值或者可以继续求值 \(t \to t'\)
强制转型,Up/Down Casting
\(S<:T\)
- 对于 \(e:S\),\((T)e\) 称为 上行转型 up-casting,是类型安全的
- 对于 \(e:T\) ,\((S)e\) 称为 下行转型 down-casting,是不安全的,往往需要运行时检查(低效的)
上行/下行转型其实就是沿着继承链向上走/向下走

算法子类型 Algorithmic Subtying
目的:用语法制导的算法类型化关系代替声明性的子类型化关系,从而实现语法制导。
去掉了 S-Trans 和 S-Refl 规则,增加了一个将字段类型的深度、广度和置换子类型化规则结合起来的规则 S-Rcd:

\(\mapsto \mathrm{S}<:T\) 表示:\(S\) 在算法上是 \(T\) 的子类型
将应用规则 T-APP 用更有力的规则 TA-APP 代替:将 T-SUB 的一条实例作为前提包括进来,使得可以完全不使用包含规则 T-SUB
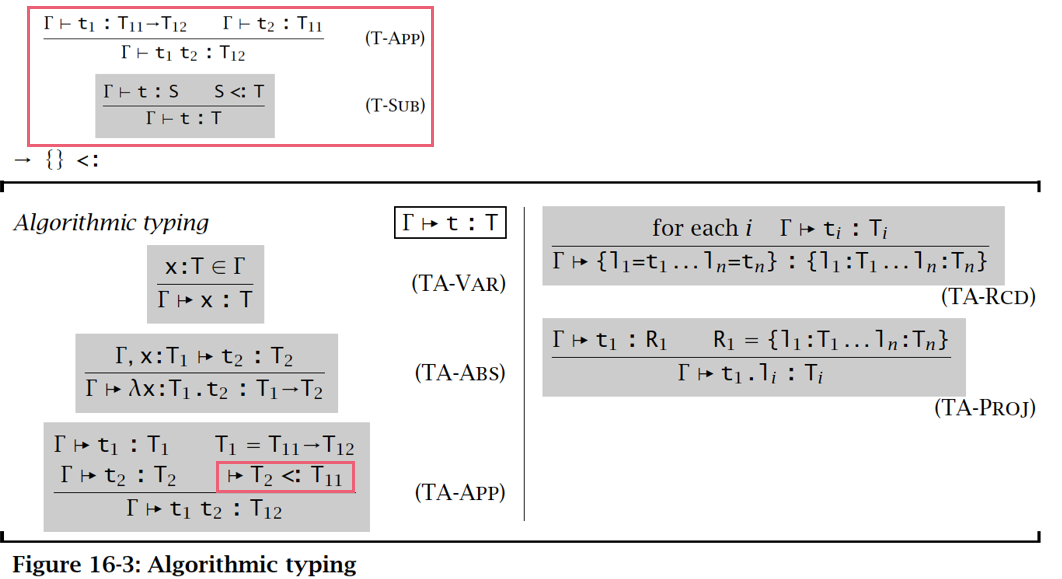
伪代码:
let rec subtype(S, T) =
match (S, T) with
|(_, Top) -> true
|(S1->S2, T1->T2) ->
subtype(T1, S1) /\
subtype(S2, T2)
|({li: Si, …}, {ki: Ti, …}) ->
{ki}⊆{li} /\
subtype(Si, Ti) // for each i
| _ -> false
算法子类型化的属性:
-
理论[可靠性]:如果 \(\Gamma \vdash \mathrm{t}: \mathrm{T}\) 并且 \(t\to t'\),那么 \(\Gamma \vdash \mathrm{t}^{\prime}: \mathrm{T}\)
Proof:算法类型推导的直接归纳
-
理论[完备性,最小类型化]:如果 \(t\) 是一个封闭的、类型良好的项,那么 \(t\) 要么是一个值或者可以继续求值 \(t \to t'\)
轻量级Java(FJ)实例分析
面向对象编程语言的特点
多重表示:当一个对象调用一个操作时,对象自行确定哪些代码被执行。
封装:对象的内部表示是隐藏的,只有对象自己的方法才能访问其内部数据。
子类型化:具有更多方法的接口是具有较少方法的接口的子类型;当需要某一类型时,提供其子类型总是安全的。
继承:定义类(实例化对象的模板)、继承父类、增加新方法、重载旧方法。
开放递归:一个方法内部能通过特殊的变量(self或this)来调用同一对象中的其他方法。
语法 & 求值语义 & 类型语义
Syntax:
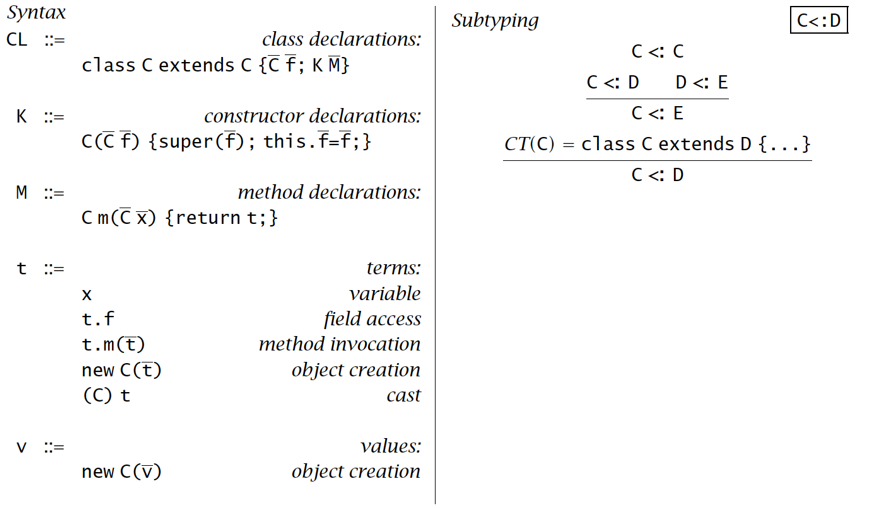
辅助定义:

求值语义:

类型语义:

递归类型 Recursive Types
递归类型:出现在其定义中的类型,可以编写无限的数据结构
-
列表 NatList = <nil:Unit, cons:{Nat, NatList}>
或 NatList = µX. <nil:Unit, cons:{Nat,X}>
其中,µ 为递归操作符。µX.T 表示X类型是由T定义的类型,T中包括 X 类型。
【例子】类型判断



- 饥饿函数(吞掉所有参数) Hungry = µA. Nat -> A
【例子】

- 流 Stream = µA. Unit ->
【例子】

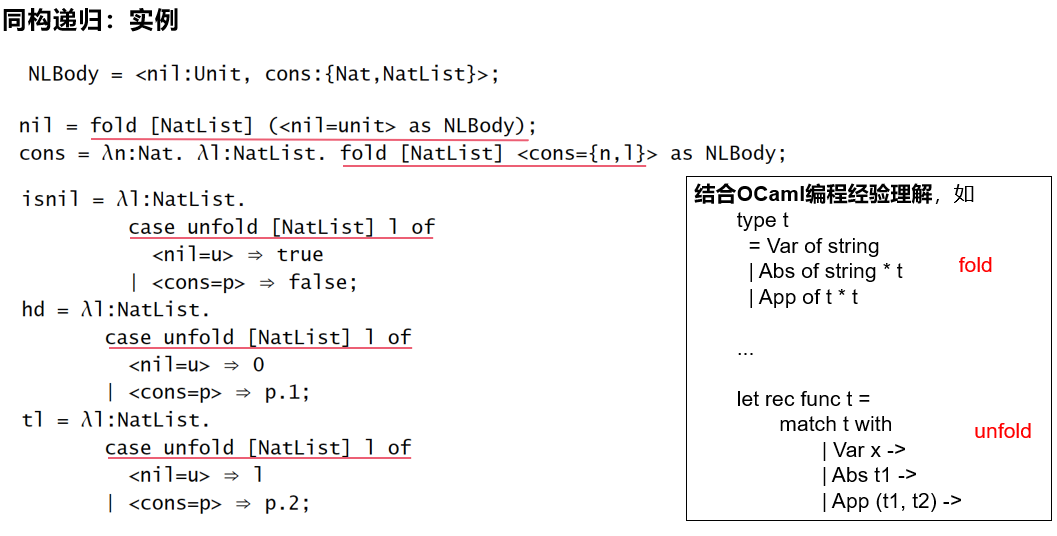
同构递归形式 Iso-recursive
递归类型 μX.T 和它的一步展开是什么关系?
- 等价递归:认为两表达式等价
- 实际应用时难以进行类型等价性检查
- 形式更轻量级
- 同构递归:认为递归类型与其展开式不同,但同构
- 方便类型检查
- 形式更重量级

同构递归 Syntax & Semantics:
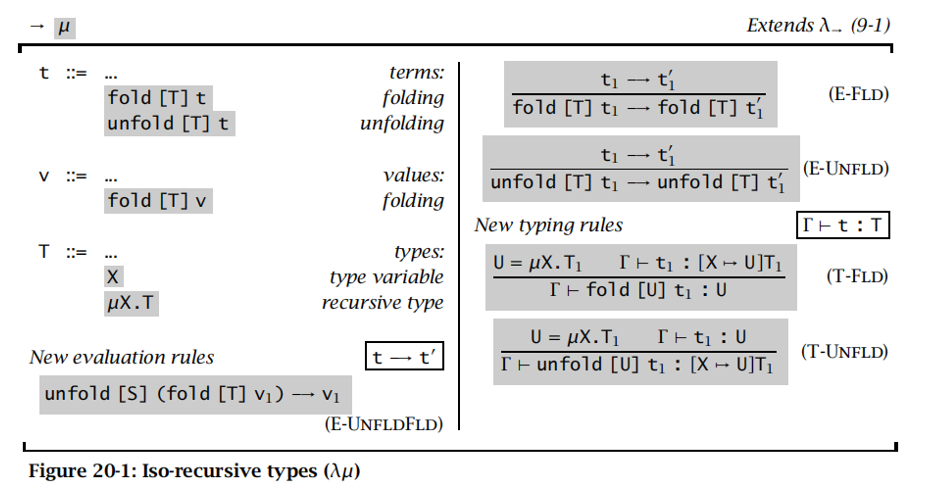
【例子】
类型重建 Type reconstruction
编程语言中,程序员希望通过编写无类型代码来减少编码量,然后让编译器进行自动推断类型(也就是所谓的类型重建)从而可以进行类型系统检查
类型变量和类型代换

类型变量:可实例化为某一基本类型,或被其它类型变量代换
类型变量的引入,让代码更加可复用(模板/泛化),结合了有类型和无类型的优点:不需要显示写出具体类型就可以拥有强类型和强类型安全
类型代换 σ:
-
定义一个从变量转换到具体类型或其他类型变量的有限映射σ。如 σ = [X|->Bool,Y|->X]
-
将该映射应用到类型变量T上(代换是同时进行的)。如上例,T=Y→Y时,σ(T) = X→X
-
代换规则:


类型重建:赋予类型变量一个具体类型
类型推断
根据 t 和 Γ 中体现的约束,选择合适的值将该项实例化为良好类型;即求解(Γ,t),通过实例化各个类型变量,使项 t 通过类型检查。
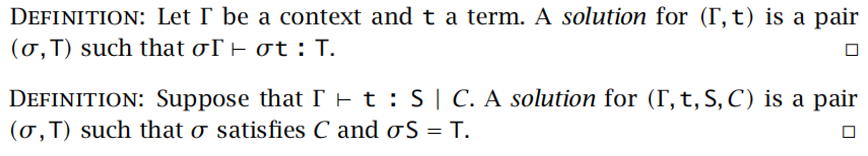
求解步骤:
- 计算约束集:根据给定的项 t,上下文 Γ,以及代表 t 的类型的类型变量 S,找到能使 t 有类型的约束集 C
- 合一算法:求解约束得到代换 σ,代换 σ 把 t 中的类型变量替换为其他类型变量或实例化为具体类型
\(\Gamma |- \mathrm{t}: \mathrm{T}| x \ \mathrm{C}\) 表示:约束集 C 满足时,项 t 在 Γ 下的类型为T
x 用于记录在每个子推导中出现的中间类型变量
约束类型规则:

给定 Γ 和 t,计算 T 和 C (以及 x),使其满足 \(\Gamma |- \mathrm{t}: \mathrm{T}| x \ \mathrm{C}\)
【例子】

合一算法:求解约束集 C 得到代换 σ
伪代码:

主类型:

对于隐性类型变量
-
解析期间,编译器填充所有缺失类型的变量,但可能执行的时间太早(所有 function application 会共享到相同的类型变量)
-
lazy 策略:
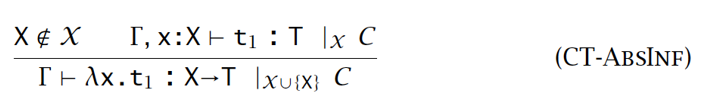
-
使用 let 多态来实现隐性类型变量
Let 多态 Let polymorphism
目的:通过抽象类型变量实现相似功能的代码的重用


在上下文Γ中对项 let x = t1 in t2 进行类型检查,步骤如下:
-
使用约束类型规则为右端的 t1 计算相关的类型 S1 和约束集合 C1
-
用合一规则为约束集 C1 找到最一般化解 σ,并将 σ 用于 S1(和Γ) 来获得 t1 的主类型 T1
-
对 T1 中的 其余变量(自由变量) 进行一般化推广(泛化),如果 X1...Xn 是剩余的变量,则 t1 的主类型模式为 ∀X1...Xn.T1
【注】不要将 Γ 中提到的 T1 也进行一般化推广,因为这些对应着 t1 与其语境之间的实际的约束
自由变量集合 = FV(t1)-FV(Γ)
-
对上下文进行扩充,将囿变量 x 的类型记为 ∀X1...Xn.T1,现在上下文会给每个自由变量一个类型模式(形如∀X1...Xn.Ti),而不是一个类型。开始对t2进行类型检查。
-
每次在 t2 中遇到变量 x,则查找 t1 的类型模式 (∀X1...Xn.T1),产生新的类型变量序列 Y1...Yn 并用其来实例化 t1 的类型模式,即产生 [X1→Y1, ... , Xn→Yn]T1,以此作为x的类型(之后据此检查 t2 的类型,即计算相关的类型 S2 和约束集合 C2,最终求解出 t2 的类型,即为整个let x = t1 in t2 的类型)
最终结果无论有多个 \(\forall\) ,都应该提取出来放在求解结果的头部(若未实例化)
【例题】

【例题2】

【例子】

万能类型 Universal Types
为什么需要多态性(Polymorphism)?
抽象原则:每个功能应该只被实现一次
例如,实现一个 f(f(x)) 的功能,期望只实现一个支持泛化类型的功能,而非针对每个具体类型再实现一次该功能:
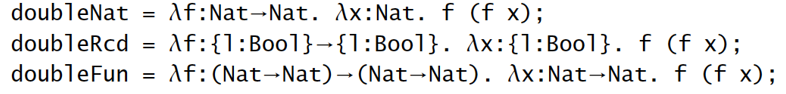
一般程序语言所需的多态特性可有:
- 参数多态(System F,例如模板和泛化)
- Ad-hoc 多态(值可以被看成各种不同类型,例如方法重载)
- 子类型多态
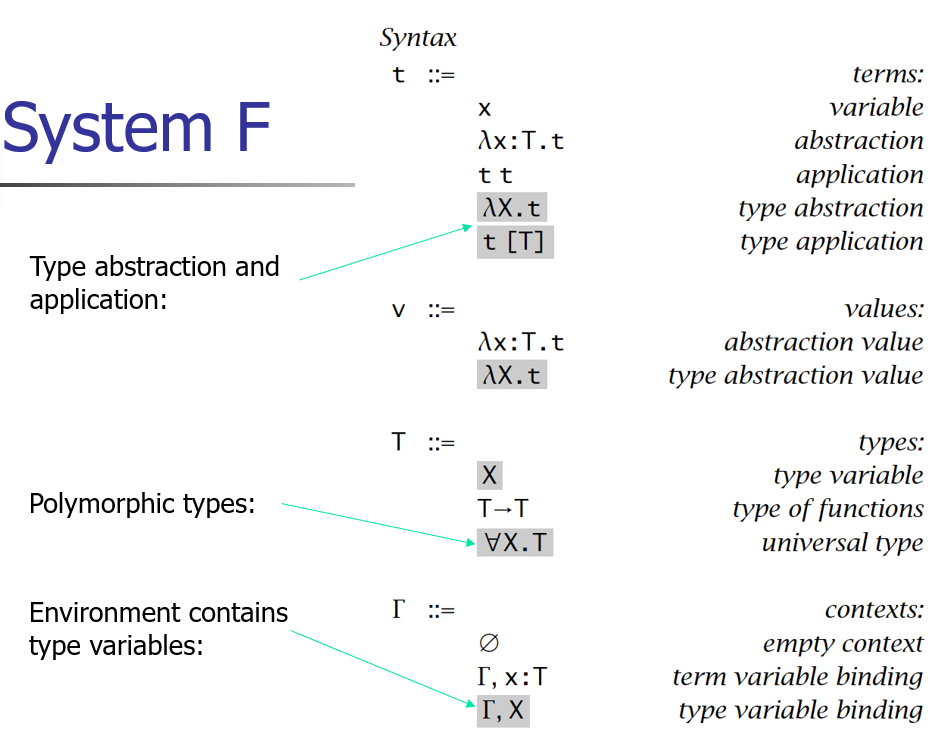
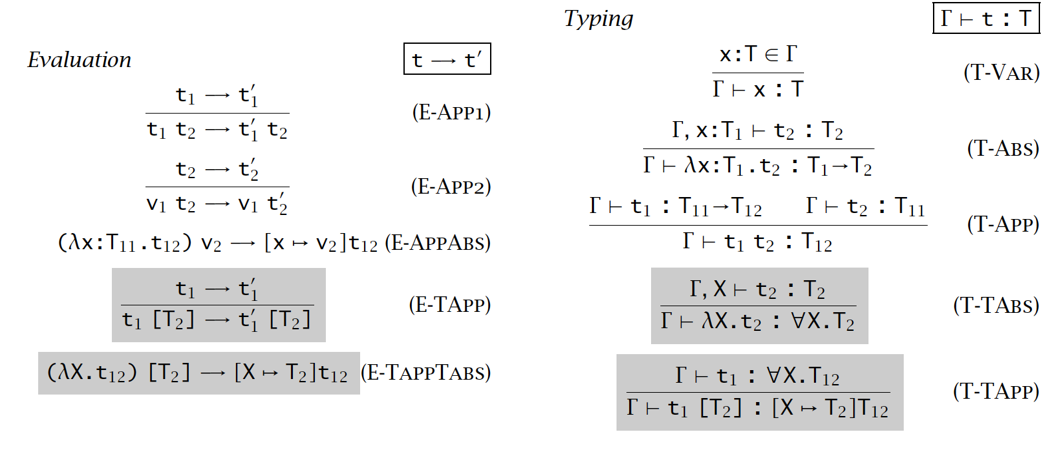
System F
把类型也当成函数参数来调用,并使用 [T] 作为具体类型参数

相当于
// C++ template template <typename X> X f(X a){return a;} f<int>(33);
【例子】标识符

【例子】double 函数

【例子】无类型项
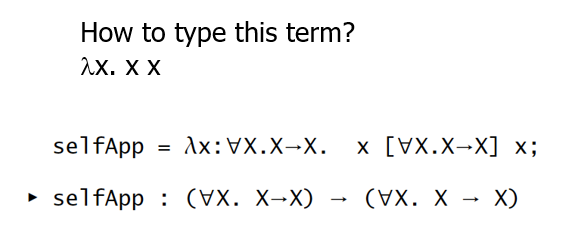
【例子】list

【例子】bool

【例子】nat

System F 的属性:
- 理论[Preservation]:如果 \(\Gamma \vdash \mathrm{t}: \mathrm{T}\) 并且 \(t\to t'\),那么 \(\Gamma \vdash \mathrm{t}^{\prime}: \mathrm{T}\)
- Proof:
- 理论[Progress]:如果 \(t\) 是一个封闭的、类型良好的项,那么 \(t\) 要么是一个值或者可以继续求值 \(t \to t'\)
- Proof:
- 理论[Normalization]:类型良好的 System F 是规范化的
System F 的其它性质:
-
二阶 polymorphism:从 root 到 \(\forall\) ,其左边没有通过 2 个或更多的 arrow
- e.g.:\((\forall X.X\to X)\to Nat\) ;\(Nat\to (\forall X.X\to X)\to Nat \to Nat\) ;\(((\forall X.X\to X)\to Nat)\to Nat\)
- 类型重建是可判定的
-
不可/可预测性:依据范式表达式是否接受它自己作为参数
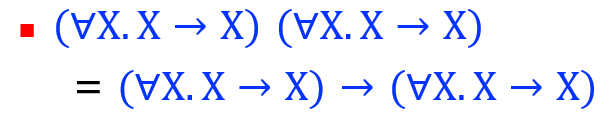
- 接受:不可预测性
- 不接受:可预测性,因为移除了矛盾

- System F 实现了参数多态,在表达更多非变量时更加强有力
- 类型重建是不可预测的(因为太过重量级的类型概念)
Erasure of Types
移除 Types
理论:以下是不可判定的:给定一个无类型 lambda 演算中的封闭项 \(m\),在 System F 中存在一些类型良好的项 \(t\) 可以使得 \(earse(t) = m\)
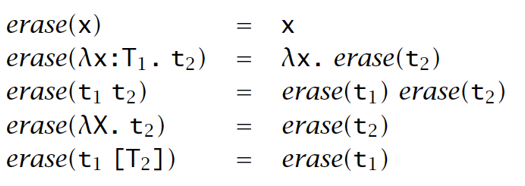
移除 Type Applications
理论:以下是不可判定的:给定一个 type applications 被标记了但参数是暴露的的封闭项 \(m\),在 System F 中存在一些类型良好的项 \(t\) 可以使得 \(earse(t) = m\)
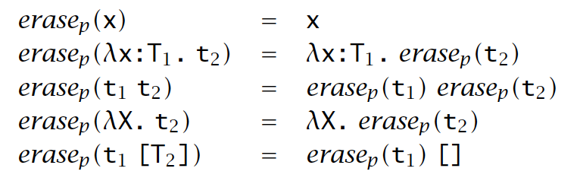
移除和求值顺序
理论:如果 \(erase_v(t) = u\) ,那要么 \(t\) 和 \(u\) 都是根据它们各自的求值关系的规范化形式,要么 \(t\to t'\) 和 \(u\to u'\),才有 \(earase_v(t') = u'\)
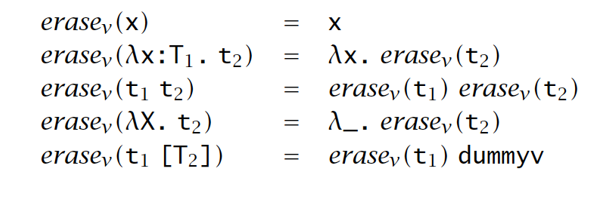
存在类型 Existential Types
目的:万能类型可被认为是表达所有谓词 \(\forall X.T\),而我们还需要表达存在谓词 \(\exist X.T\)
逻辑直觉上: 一个 \(\{\exist X, T\}\) 元素意味着存在某些类型 \(S\) 使它的值为 \([X|-> S]T\)
操作直觉上:一个 \(\{\exist X, T\}\) 元素意味着它是一个二元组 \(\{*S, t\}\) ,其中 ;就像模块或者 ADT 那样

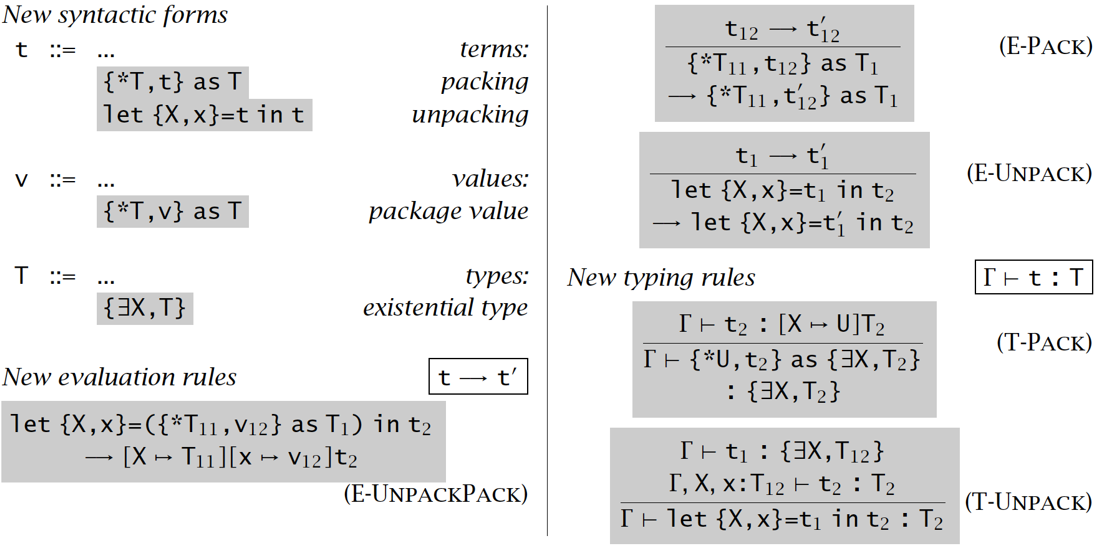
【例子1】T-PACK
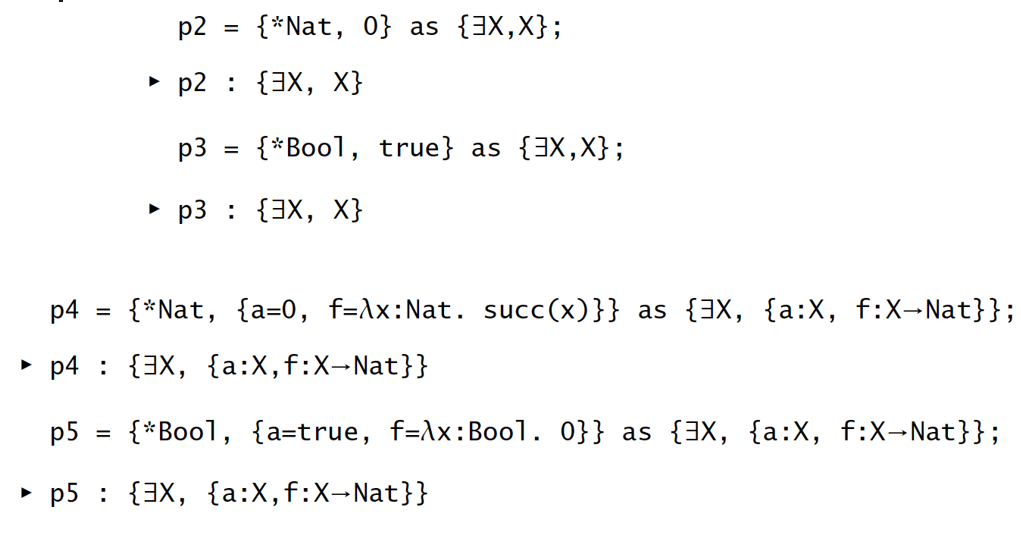
【例子2】T-UNPACK
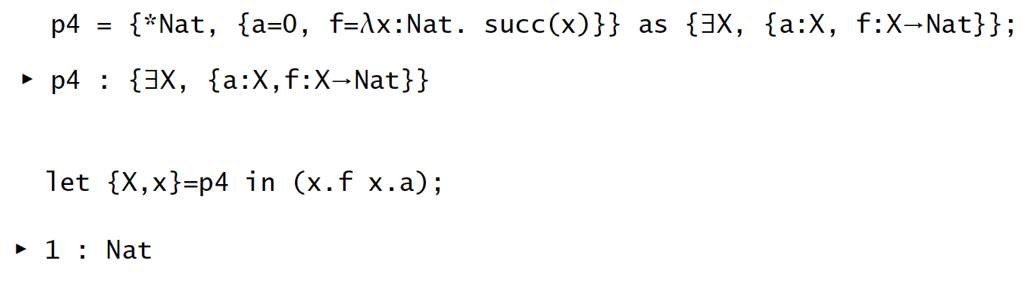
抽象会被保留:
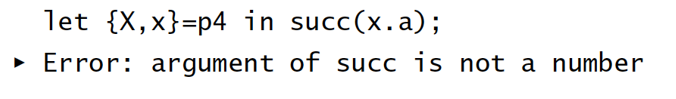
结论中不会出现类型变量:

数据抽象 Data Abstraction
数据抽象主要两种形式:
- ADT(Abstract data types),由下列元素组成
- 类型名 \(X\)
- 具体代表类型 \(T\)
- 一组操作类型 \(T\)
- 一个抽象边界
- Objects:
- 内部状态 \(X\)
- 一组操作状态的方法 \(T\)

总结:
- 存在类型强制抽象或信息隐藏,是一个很好的抽象概念用于ADT或对象建模
- 限制了程序的变化
- 限制了依赖性
- 鼓励开发者去抽象地思考
- 表示的独立性:
- 具体表示能被代换成可选的一种
类型操作符 Type Operators
期望实现类型层次的计算,或者更说求类型操作(类似于值的求值操作):

template <typename X, typename Y> class Pair{ X a; Y b; public: Pair(X a, Y b){…} } int main(){ Pair p; // type error! Pair<int, int> p; // 支持 type-level }也期望可以判断类型的等效性(就像通过类型判断值的等效性):

类型 application 也可能是无意义的(期望有比类型更高层的抽象规则约束掉这种类型 application):

类型操作符就是在类型层次的函数,为此需要将抽象上升一个 kind 层级( kind 之于类型,其实就是类型之于值)

【例子】

一个引入 kind 层(用于支持类型操作符)的系统:
- 该系统的类型检查是非平凡的
- 类型等效是非平凡的
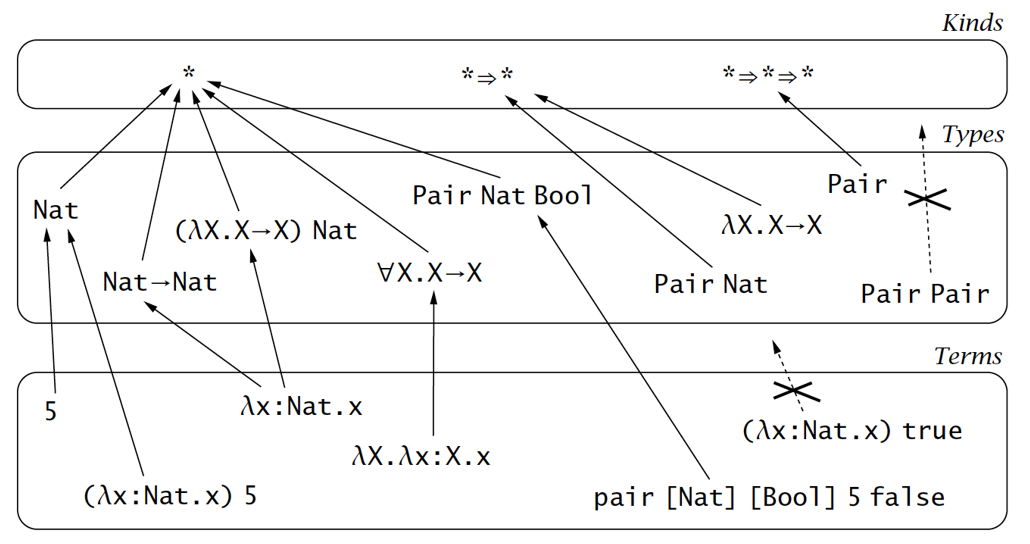
为什么没有超过三个层级?其实类型理论学家已经研究超过三层的系统(称为pure type systems),但主流编程语言并没有采纳该系统,而且3层已经足够一般的程序生涯了
System λω
加入了支持类型操作符的有类型λ演算包含:
- 语法:
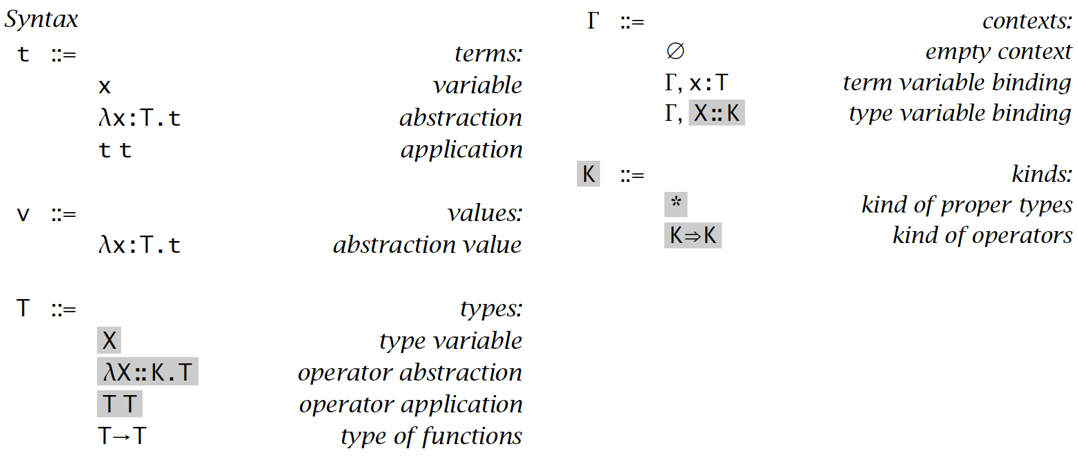
- 求值规则:
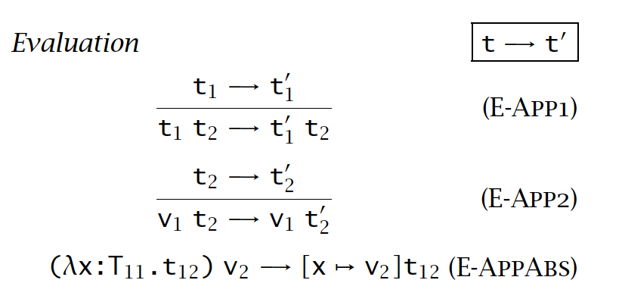
- 类型规则:
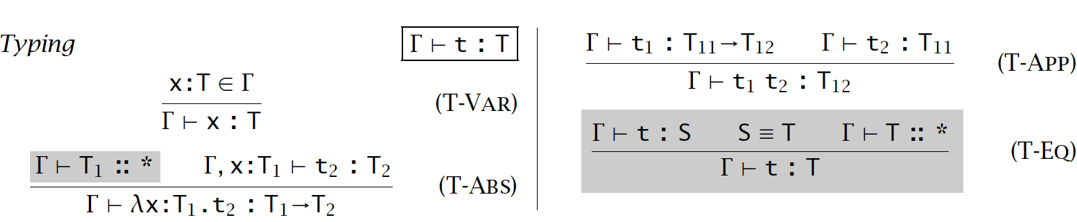
-
类型等价:
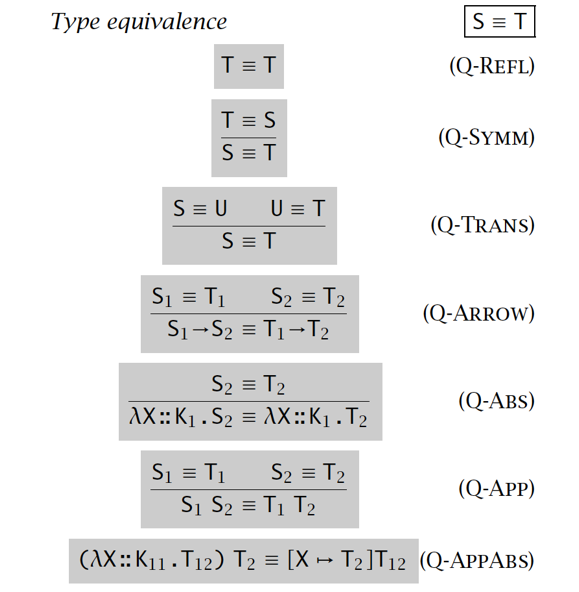
-
kinding 规则:
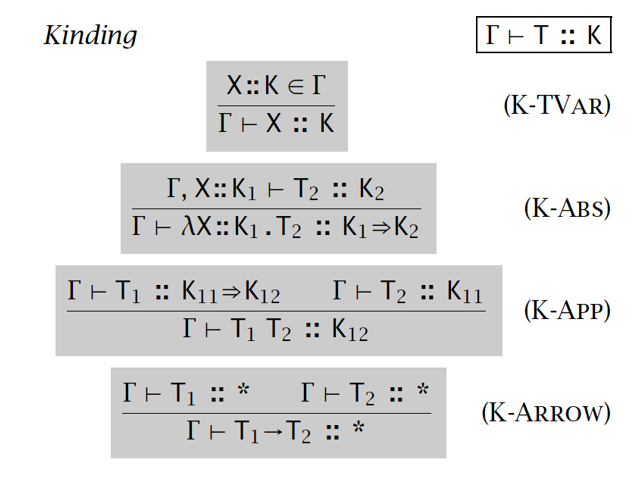
更高层次多态 Higher-Order Polymorphism
System Fω
System F 实现了多态函数
System λω 实现了多态类型

System Fω:结合多态函数+多态类型
【例子】:
- 语法:

- 求值规则:

- 类型规则:

- 类型等价:

- kinding 规则:
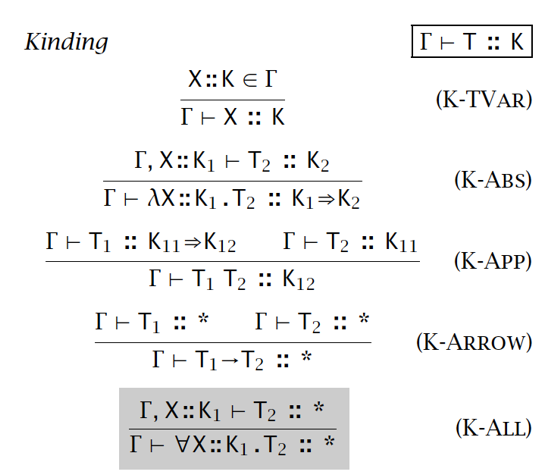
- 扩展的存在量词:

【例子】

System Fω:
- 是非平凡的:计算基于类型而不仅仅是项
- 满足类型安全:理论[Preservation]+理论[Progress]
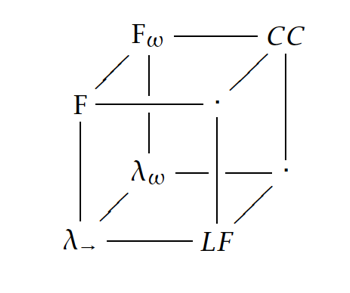
- Barendregt cube:呈现了干净且同一的结构纯类型系统
作者:KillerAery
出处:http://www.cnblogs.com/KillerAery/
本文版权归作者和博客园共有,未经作者同意不可擅自转载,否则保留追究法律责任的权利。

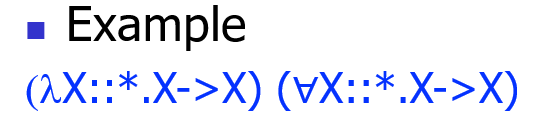

 浙公网安备 33010602011771号
浙公网安备 33010602011771号