实时阴影技术（1）Shadow Mapping

目录

• Shadow Mapping
  • Shadow Bias
  • Peter Panning 问题 & 简单 Trick
  • Slope Scale Based Depth Bias
• Percentage Closer Filtering（PCF）
  • 分布采样函数
  • PCF 算法过程
  • 硬件 PCF
• Percentage Closer Soft Shadows（PCSS）
  • Penumbra Size
  • Blocker Search
  • PCSS 算法过程
  • Penumbra Mask
• Filtered Shadowmap
  • Variance Soft Shadow Mapping（VSSM）
    • 计算平均值 & 方差
    • 计算累计分布函数（CDF）
    • 加速 Blocker Search 算法
    • 加速 PCF 算法
    • VSSM 的缺陷
  • Moment Shadow Mapping（MSM）
  • Exponential Shadow Mapping（ESM）
    • Log 空间存储
  • Exponential Variance Shadow Map（EVSM）
• Cascade Shadow Map（CSM）
  • 视锥分割
  • 计算包围盒
  • 层级选择
  • 分帧更新
  • Stablize CSM
• Virtual Shadow Map
  • Clipmaps
  • 稀疏内存管理
  • 算法过程
• Per Object Shadow
  • 自阴影
  • 结合 Shadow Volume 技术
  • 延迟阴影管线
• Shadow Caster Culling [预计算]
  • Shadow Caster & Shadow Receiver
  • Precomputed Shadows
  • PVS（Potential Visible Set）
• Shadow Caster Culling [运行时]
  • Shadow Map Caching [2012]
  • 遮挡剔除
  • 视锥剔除
  • Receiver Mask [2011]
• 参考

Shadow Mapping

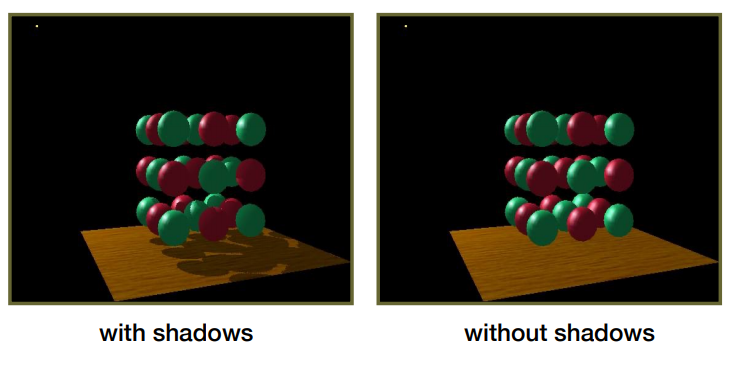
Shadow Mapping 基本原理：

1. 阴影生成 Pass：
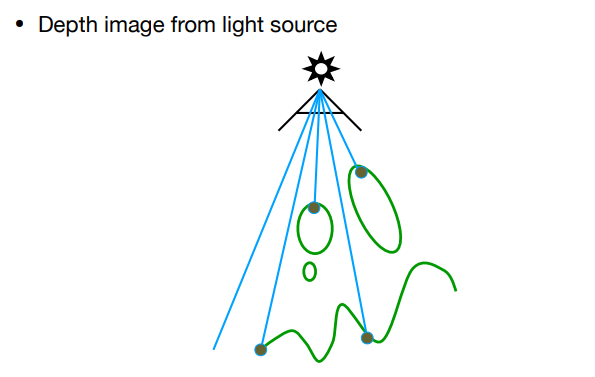
   • 额外设置一个摄像机在光源位置（Light Camera，光源摄像机），并且朝光照方向看去。
   • 用一张 Texture（称为 阴影贴图 Shadow Map）来记录 Light Camera 所看到的像素深度（每个像素位置只记录所见最近深度，而不用做别的 shading 计算）来作为遮挡深度。

// shadowVertex.glsl
// ...
void main(void) {
  vNormal = aNormalPosition;
  vTextureCoord = aTextureCoord;
  gl_Position = uLightMVP * vec4(aVertexPosition, 1.0);
}

// shadowFragment.glsl
// ...
void main(){
  gl_FragColor = pack(gl_FragCoord.z);
}

如图，Shadow Map 记录了 Light Camera 所看到的最近深度图，颜色越深，离摄像机越近：

2. 渲染 Pass：
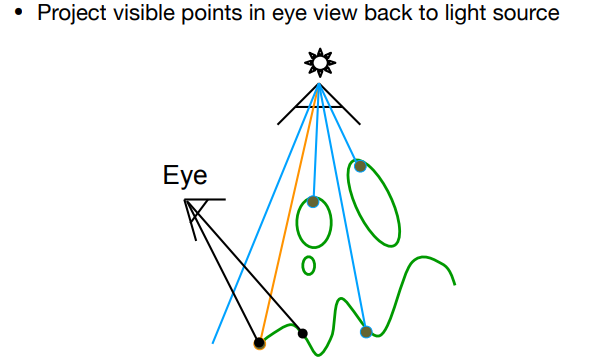
   • 主摄像机需要渲染屏幕每个像素时，该像素对应的世界坐标进行 Light Camera 的MVP变换后能得到在 Light Camera 屏幕空间中的对应位置 \(shadowCoord = (x',y',z')\)。
   • Shadow Map 里用\((x',y')\)采样得到的遮挡深度 \(depth\) 与深度值 \(z'\) 做比较： 若 \(depth < z'\)（意味着该像素的光被遮挡），这时就可以对该像素降低可见度（Visibility）。

// phongVertex.glsl
// ...
void main(void) {
  vNormal = (uModelMatrix * vec4(aNormalPosition, 0.0)).xyz;
  vTextureCoord = aTextureCoord;
  vFragPos = (uModelMatrix * vec4(aVertexPosition, 1.0)).xyz;
  vPositionFromLight = uLightMVP * vec4(aVertexPosition, 1.0);
  gl_Position = uProjectionMatrix * uViewMatrix * uModelMatrix * vec4(aVertexPosition, 1.0);
}

// phongFragment.glsl 
// ...
void main(){
    // 归一化坐标
    vec3 projCoords = vPositionFromLight.xyz / vPositionFromLight.w;
	vec3 shadowCoord = projCoords * 0.5 + 0.5;
    // Shadow
	float visibility = 1.0;
	float depthInShadowmap = unpack(texture2D(shadowMap,shadowCoord.xy).rgba); //将rgba四通道（32位）的值unpack成float类型的数值
	if(depthInShadowmap < shadowCoord.z){
    	visibility = 0.0;
	}
    // blinnPhong光照着色
    vec3 color = blinnPhong();
    
    gl_FragColor = vec4(color * visibility,1.0);
}

如图为主摄像机每个像素经过变换后比较深度的结果，其中绿色点意味着深度 \(depth \approx z’\) （没有遮挡光照），非绿色点意味着 \(depth < z'\)（被遮挡了光照）:

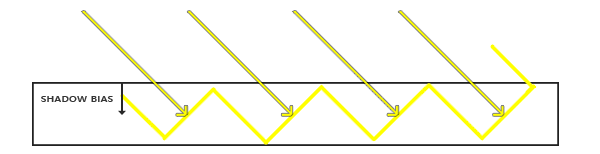
Shadow Bias

直接使用Shadow Map可能会在不应该出现阴影的位置出现一些黑白条纹相间的现象（称为 Shadow Acne）：

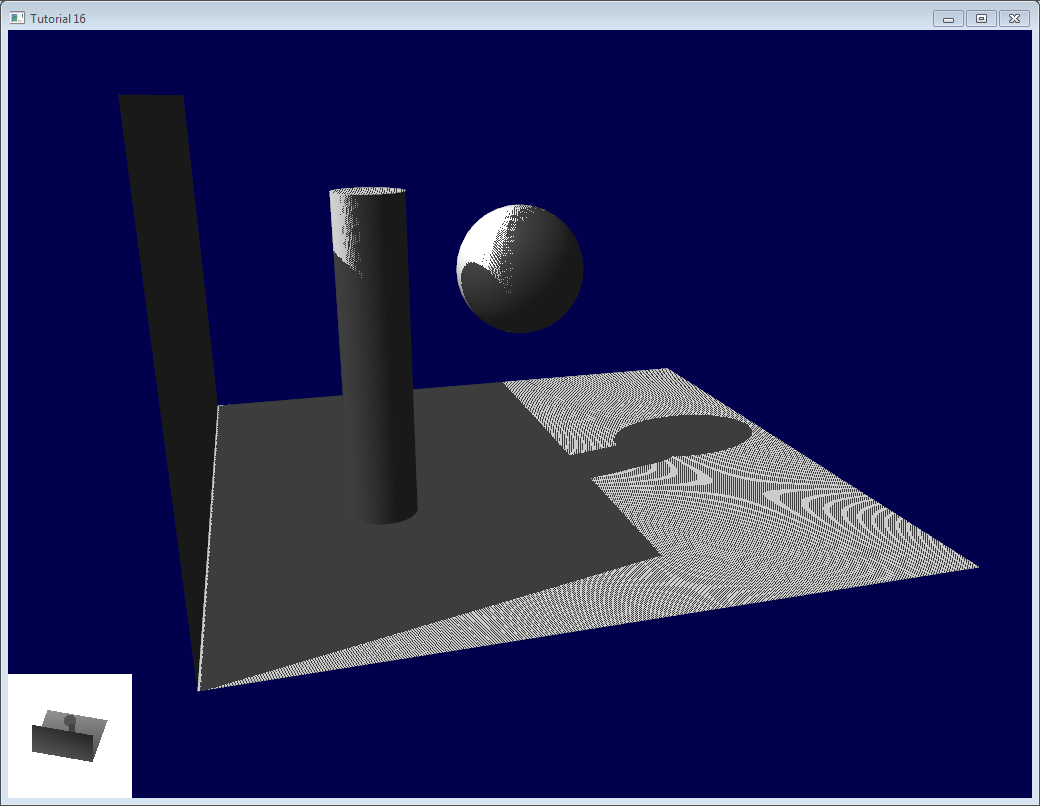
其本质原因在于，Shadow Map 是一个二维数组，离散的存储方式很难完全表示实际的几何信息。尤其当光照方向不垂直于平面时，遮挡深度的采样会和实际深度产生偏差（如图一个不受遮挡的几何平面，但黑色加粗部分却被Shadow Mapping方法认为是被遮挡的）：

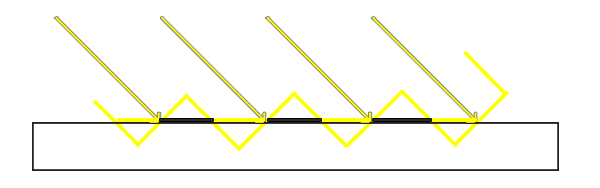
解决方法：

• 直接给采样阴影深度加一个 偏移量 Bias（相当于把阴影深度往远处加，从而更不容易产生遮挡）。

// phongFragment.glsl
//...
void main(){
    // 归一化坐标
    vec3 projCoords = vPositionFromLight.xyz / vPositionFromLight.w;
	vec3 shadowCoord = projCoords * 0.5 + 0.5;
    // Shadow Bias
	const float BIAS = 0.005;
    // Shadow
	float visibility = 1.0;
	float depthInShadowmap = unpack(texture2D(shadowMap,shadowCoord.xy).rgba); //将rgba四通道（32位）的值unpack成float类型的数值
	if(depthInShadowmap + BIAS < shadowCoord.z){
    	visibility = 0.0;
	}
    // blinnPhong光照着色
    vec3 color = blinnPhong();
    
    gl_FragColor = vec4(color * visibility,1.0);
}

Peter Panning 问题 & 简单 Trick

然而由于增加了Bias，可能会导致 Peter Panning 现象：往往在物体缝隙间发生漏光。

解决方法：

• 避免使用单薄的几何体（例如薄墙、薄地面）；只要几何体厚度大于Bias，影子边界便会产生在几何体内部，从而不易看见影子与几何体的分离现象。

有一种有别于Bias的方法（但实际上也是殊途同归）：

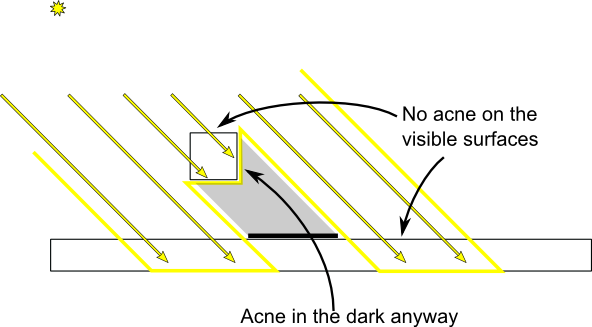
• 不使用Bias

• 第一个Pass（Light Camera记录深度的那个）设置成仅渲染背面（正面剔除）

这样可以让一些具有厚度的几何体背面作为深度记录，从而部分避免了几何体正面的 Shadow Acne现象。实际上这个跟使用了Bias+加厚几何体思想是差不多的，区别只不过在于：前者是低门限加一个偏移，后者则是直接给出高门限

Slope Scale Based Depth Bias

通过上面知道，Bias 过小时可能不能解决 Shadow Acne 现象，Bias 过大时又可能导致严重的 Peter Panning问题。

Slope Scale Based Depth Bias ：为了尽可能减少由于 Bias 过大过小引起的问题，采取了根据平面倾角的一种自适应 Bias（例如：当光线与平面垂直时，Bias应该为0；当光线与平面的夹角越小，则Bias应越大）。

float bias = max(0.05 * (1.0 - dot(normal, lightDir)), 0.005);

Percentage Closer Filtering（PCF）

Shadow Mapping 还存在 阴影锯齿（Shadow Aliasing） 问题：

Percentage Closer Filtering（PCF）正是解决阴影锯齿的方案，它的核心想法是计算阴影时不是考虑单个采样点，而是在一定范围内进行多重采样，这样可以让阴影的边缘不那么锯齿，因为 Visibility 不再是非0即1，而是带有渐变的取值。

分布采样函数

vec2 disk[NUM_SAMPLES]; // 经过分布采样函数运算后得到NUM_SAMPLES个采样坐标

在对周围一定范围内若干个坐标进行采样的时候，可以通过分布采样函数来确定 NUM_SAMPLES 个采样位置，为了让阴影边缘更加柔和，我们可以用一些较好的分布采样函数。

均匀圆盘分布采样（Uniform-Disk Sample）：圆范围内随机取一系列坐标作为采样点；看上去比较杂乱无章，采样效果的 noise 比较严重。

泊松圆盘分布采样（Poisson-Disk Sample）：圆范围内随机取一系列坐标作为采样点，但是这些坐标还需要满足一定约束，即坐标与坐标之间至少有一定距离间隔。

// 均匀圆盘分布
void uniformDiskSamples( const in vec2 randomSeed ) {
  // 随机种子
  float randNum = rand_2to1(randomSeed);
  // 随机取一个角度
  float sampleX = rand_1to1( randNum ) ;
  float angle = sampleX * PI2;
  // 随机取一个半径
  float sampleY = rand_1to1( sampleX ) ;
  float radius = sqrt(sampleY);
  for( int i = 0; i < NUM_SAMPLES; i ++ ) {
    disk[i] = vec2(radius * cos(angle) , radius * sin(angle));
    // 继续随机取一个半径
    sampleX = rand_1to1( sampleY ) ;
    radius = sqrt(sampleY);
    // 继续随机取一个角度
    sampleY = rand_1to1( sampleX ) ;
    angle = sampleX * PI2;
  }
}

// 泊松圆盘分布
void poissonDiskSamples( const in vec2 randomSeed ) {
  // 初始弧度
  float angle = rand_2to1( randomSeed ) * PI2;
  // 初始半径
  float INV_NUM_SAMPLES = 1.0 / float( NUM_SAMPLES );
  float radius = INV_NUM_SAMPLES;
  // 一步的弧度
  float ANGLE_STEP = 3.883222077450933;// (sqrt(5)-1)/2 *2PI
  // 一步的半径
  float radiusStep = radius;

  for( int i = 0; i < NUM_SAMPLES; i ++ ) {
    disk[i] = vec2(cos(angle),sin(angle)) * pow( radius, 0.75 );
    radius += radiusStep;
    angle += ANGLE_STEP;
  }
}

PCF 算法过程

Percentage Closer Filtering（PCF） 的算法过程：

1. 计算 Visibility 时，原本对 Shadow Map 的一次坐标采样换成对周围一定范围内若干个坐标进行采样。
2. 各个采样结果同样用来与 \(z'\) 做比较，最后取比较结果的平均作为 Visibility。

float visibility_PCF(sampler2D shadowMap, vec4 coords) {
  const float bias = 0.005;
  float sum = 0.0;
  // 初始化泊松分布
  poissonDiskSamples(coords.xy);
  // 采样
  for(int i = 0;i<NUM_SAMPLES;++i){
    float depthInShadowmap = unpack(texture2D(shadowMap,coords.xy+disk[i]*0.001).rgba);
    sum += ((depthInShadowmap + bias)< coords.z?0.0:1.0);
  }
  // 返还平均采样结果
  return sum/float(NUM_SAMPLES);
}

硬件 PCF

所谓硬件 PCF 技术就是利用纹理采样器中的 compare func（如 DX11 中为 D3D11_COMPARISON_LESS_EQUAL）来实现深度大小比较计算，这样对 shadow map 采样一次的结果返还的不是阴影深度而是深度比较后的布尔结果（0或1），并且同时还需要启用 linear sampling 从而可以得到 2x2 texels filter 后的采样结果。

• 硬件 PCF 非常快速，只需一次采样操作即可完成，无需额外代码。

然而硬件 PCF 只能计算 2x2 个 samples，只能让阴影边缘有一定程度的软化，并不能完全消除锯齿。为此还可以进一步利用硬件 PCF 技术，我们进行更多次这样的硬件采样，就可以得到更多 samples 的结果。例如，进行 4 次硬件采样就可以获得 4×4 个 samples 的结果：

Percentage Closer Soft Shadows（PCSS）

Shadow Mapping 还存在硬阴影（Hard Shadow）的问题，因为现实世界的影子往往是软阴影（Soft Shadow）。

一个现实观察是，当投影物与阴影之间的距离越远，则阴影越软（如下图：笔尖阴影由于与笔尖的距离较近，因此阴影边缘较为锐利；而远处笔身阴影则因与笔身距离较远，阴影边缘较为发散且模糊）。

这是因为较大的光源面会有一些区域被遮蔽一部分光又接受一部分光，从而产生半影（Penumbra），直观看就是没那么暗的边缘处阴影。

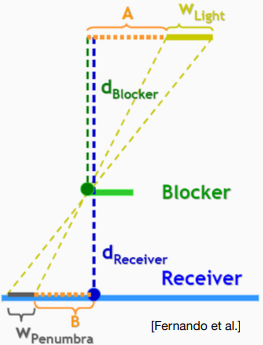
Penumbra Size

用二维平面的图去描述，实际上就是光源段 \(w_{Light}\) 两端与遮挡物连直线后打在被投影物上的即是 半影段 \(w_{Penumbra}\) ，也就是说这段半影需要有渐变的阴影效果。假如我们用 PCF 算法中的圆盘半径大小等同于这个半影段的尺寸 \(w_{Penumbra}\)，就能实现这段的渐变阴影效果（可以想想为什么）。

现在，由下图的几何关系容易推出：

\[w_{\text {Penumbra }}=\left(d_{\text {Receiver }}-d_{\text {Blocker }}\right) \cdot w_{\text {Light }} / d_{\text {Blocker }} \]

其中，\(w_{Light}\) 是光源面积尺寸，\(d_{Blocker}\) 是遮挡物的深度，\(d_{Receiver}\) 是被投影物的深度（实际上就是 \(z‘\)）。

但是 PCF 算法的圆盘半径大小是固定的，因此处处的边缘看起来都带有相同的渐变范围，这和我们看到的笔尖阴影现象不符合（近处边缘渐变应该更少些，远处边缘渐变应该多些），所以我们可以只要根据不同位置动态地修改圆盘半径大小（实际上就是动态地计算 \(w_{Penumbra}\) ），这个也就是PCSS的核心部分。

Blocker Search

我们不能简单把一个投影点变换成Shadow Map的坐标后，直接拿单个坐标采样 ShadowMap 的深度来作为 \(d_{Blocker}\) 。这是因为投影点的单次采样实际上就是单一直线连向了光源面的中心，而这条直线要是没有碰到遮挡物（即 \(d_{Blocker}=d_{Receiver}\) ），从而得出该投影点为全亮的结论。

但实际很多场景中（如下图），投影点和光源面处处连线后会发现有相当一部分光线会碰到遮挡物，因此该投影点应该属于半影范围内。

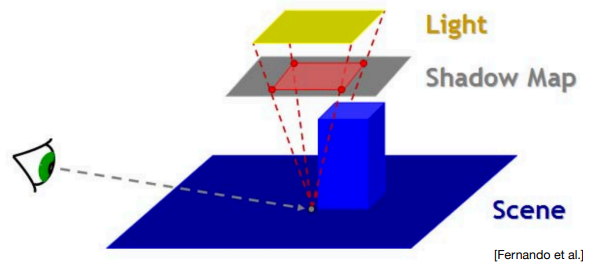
为此，我们可以对 ShadowMap 的一定范围内进行多重采样，每次采样得到的深度若小于 \(d_{Receiver}\) 则认为遇到遮挡物并算入平均遮挡深度的贡献，这样多重采样之后得到的平均遮挡深度就作为 \(d_{Blocker}\)。

如何确定采样的范围半径呢？两个参数决定：\(w_{Light}\) 的尺寸、投影点与光源的距离（可以结合上图推理一下为什么）

\[w_{blockersearch}=w_{Light}\cdot z_{Receiver} \cdot c \]

这样，计算 Blocker 平均遮挡深度的整个过程为：

float findBlocker( sampler2D shadowMap, vec2 uv, float zReceiver ) {
  float dBlocker = zReceiver * 0.01;
  const float wLight = 0.006;
  const float c = 100.0;	
  float wBlockerSearch = wLight * zReceiver * c;
  float sum = 0.01;	// 取0.01一是为了避免出现0除问题，二是当多重采样没有贡献时的dBlocker/sum将等于zReceiver
  for(int i = 0;i<BLOCKER_SEARCH_NUM_SAMPLES;++i){
    float depthInShadowmap = unpack(texture2D(shadowMap, uv + disk[i] * wBlockerSearch).rgba);
    if(depthInShadowmap < zReceiver){
      dBlocker += depthInShadowmap;
      sum += 1.0;
    }
  }
  return dBlocker/float(sum);
}

PCSS 算法过程

Percentage Closer Soft Shadows（PCSS） 的算法过程：

1. Blocker Search：通过多重采样，计算出平均遮挡深度 \(d_{Blocker}\)

2. Penumbra Size：计算圆盘半径大小 \(w_{\text {Penumbra }}=\left(d_{\text {Receiver }}-d_{\text {Blocker }}\right) \cdot w_{\text {Light }} / d_{\text {Blocker }}\)

3. Filtering：通过多重采样，计算出平均 Visibility（实际上就是调用PCF算法）

float visibility_PCSS(sampler2D shadowMap, vec4 coords){
  poissonDiskSamples(coords.xy);
  // STEP 1: avgblocker depth
  float dBlocker = findBlocker(shadowMap,coords.xy,coords.z);
  // STEP 2: penumbra size
  const float wLight = 0.006;
  float wPenumbra = (coords.z-dBlocker)/dBlocker * wLight;
  // STEP 3: filtering
  const float bias = 0.005;
  float sum = 0.0;
  for(int i = 0;i<PCF_NUM_SAMPLES;++i){
    float depthInShadowmap = unpack(texture2D(shadowMap, coords.xy + disk[i] * wPenumbra).rgba);
    sum += ((depthInShadowmap + bias)< coords.z?0.0:1.0);
  }
  return sum/float(PCF_NUM_SAMPLES);
}

PCF算法效果图：

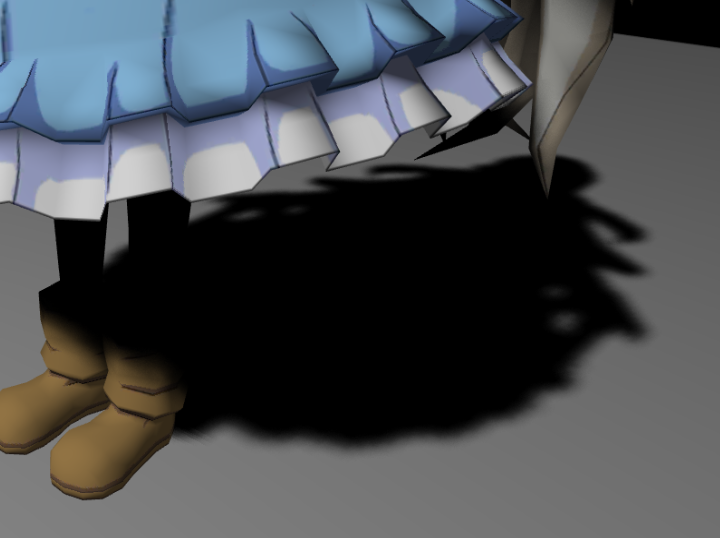
PCSS算法效果图：

Penumbra Mask

PCSS 是比较耗时的计算（需要 blocker search 采样和 PCF 采样），但实际上很多全阴影区或者全光照区是不需要软阴影效果的（它们的 shadow factor 非0即1），只有半影区是需要进行软阴影计算的。

• 可以先对每个 pixel 进行 blocker search，blocker search 的样本也同时用于与 pixel 在 shadow map space 的深度作比较；如果比较结果为部分样本被遮蔽而另一部分样本不被遮蔽，则意味着该 pixel 位于半影区，这时候才进行后续的 PCF 采样。
• 先用硬阴影技术生成 screen space shadow mask texture，然后对这张 shadow mask texture 进行边缘检测，将处于边缘的 pixels 标记出来；之后在进行一个 full-screen shader 来对有标记的 pixels 进行 PCF 计算。

可能一个 full-screen 的边缘检测本身就是比较耗时的 pass，所以可能还得想个性能更优的方式，这里就抛砖引玉一个基于 tile 的边缘检测想法：先根据 tile 内各个 pixel 的 shadow mask 情况来判断出当前 tile 属于完全遮蔽还是完全不遮蔽亦或半影；接着每个 tile 读取周围 8 个 tiles 的 mask，如果本 tile 为 shadowed 而存在相邻 tile 为 unshadowed（亦或相反的情况），则本 tile 也应该为 penumbra。最后我们只对 penumbra tiles 里的 pixel 进行昂贵的 PCF/PCSS 计算。

Filtered Shadowmap

PCF 和 PCSS 都属于一些基于空间滤波的软阴影方法，但是实时进行空间滤波往往会比较费。实际上还有另一类基于预过滤的软阴影方案，通过预过滤来减少实时滤波的开销，主要代表方案有以下：

方案	使用通道数	保存的参数
VSSM	2	\(d\), \(d^2\)
MSM	4	\(d\),\(d^2\),\(d^3\),\(d^4\)
ESM	1	\(e^{c\cdot d}\)
EVSM	4	\(e^{cd}\),\(e^{2cd}\),\(-e^{-cd}\),\(e^{-2cd}\)

Variance Soft Shadow Mapping（VSSM）

PCSS、PCF 的算法都需要多重采样，尤其 PCSS 需要两个多重采样（第一步的Blocker Search和第三步的PCF），这使得算法速度较慢。

为了避免多重采样的计算，Variance Soft Shadow Mapping（VSSM） 假定一定范围内的深度的分布符合 正态分布（Normal Distribution） ，那么只要知道该段范围的 均值（实际上就是期望值）E 、方差 Var，就能先得到该范围的正态分布模型（即知道对应的 概率密度函数 PDF）。

\[PDF(x) = \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right) \]

其中，\(\mu = E\)，\(\sigma^2 = Var\)。

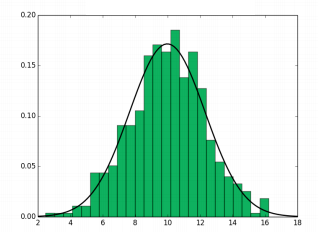
接着可以通过该正态分布模型的 累计分布函数（即 CDF），就能快速推算出该范围内有多少比例的 x 大于（或小于）给定的某个值。

\[CDF(x) = \int^x_{-\infin} PDF(t) \mathrm{d}t \]

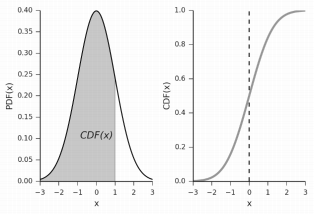
Variance Soft Shadow Mapping（VSSM） ：简单来说，VSSM 算法就是依据 ShadowMap 的深度符合正态分布的假设来快速完成 PCSS 中的第一步（Blocker Search）和第三步（PCF算法）的一种阴影算法。

VSSM效果图：

计算平均值 & 方差

为了快速查询得到某块范围的均值、方差，我们可以先选以下一种数据结构来快速查询 Shadow Map 某段范围的均值（期望值）\(E(X)\) 。

• 硬件 Mipmap：当 Shadow Map 更新时，需要重新生成 Mipmap，不过GPU硬件实现的 Mipmap 算法非常快的开销非常小；查询某段方形范围时，需要根据方形中心所在的位置（相对于周围四个纹素的坐标）、上下层级做三线性插值（Trillinear interpolation），得到的结果即是近似的均值（期望值）。

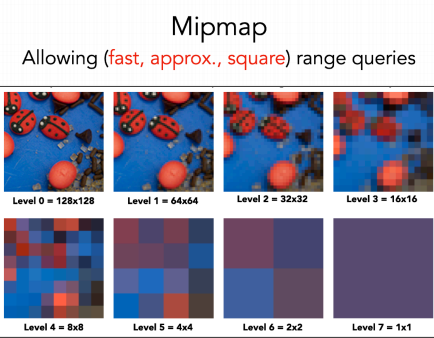
• 前缀和数组（Summed Area Tables/SAT）：当 Shadow Map 更新时，需要重新进行二维前缀和计算；需要编写 Compute Shader 实现该算法，比Mipmap方法更慢一些，但百分百精准；查询某段方形范围时，就可以通过如下图方法快速查询得到某段范围的总和，除掉范围面积就能得到均值（期望值）。

我们需要存储 \(E(X)\)、\(E(X^2)\)​ ，这样就能计算某段范围的平均值、方差：

1. 平均值 \(E(X)\)

2. 方差 \(Var(X)=E(X^2)-E^2(X)\)

\(E(X^2)\) 即 ShadowMap 每个纹素再求个平方后作为额外的ShadowMap，然后再生成 Mipmap 或 SAT。

计算累计分布函数（CDF）

有了上面的期望值与方差，我们就能确定一个正态分布。但是它对应的 CDF 函数是没有解析解的，而有数值解（称为 Error Function），但是计算比较繁琐。

切比雪夫不等式（Chebyshev’s Inequality）：

\[P(x>t) \leq \frac{\sigma^{2}}{\sigma^{2}+(t-\mu)^{2}} \]

实际上这个切比雪夫不等式不仅可用在正态分布，其它的很多分布也是可以套用这个不等式的。

将这个不等式改造一下，就成了一个大胆的近似公式：

\[P(x>t) \approx \frac{\sigma^{2}}{\sigma^{2}+(t-\mu)^{2}} \]

注意：这里求的是 \(x>t\) 的部分，即 \(P(t)=1-CDF(t)\)。

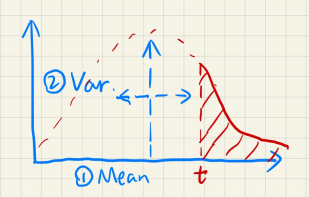
当然这个近似公式肯定不是精确的，但是计算开销非常小，也就被用在 VSSM 算法中。

加速 Blocker Search 算法

PCSS 算法中的 Blocker Search 步骤：在一定范围内多重采样，每次采样得到的深度若小于 \(d_{Receiver}\) 则认为遇到遮挡物并算入平均遮挡深度的贡献，这样多重采样之后得到的平均遮挡深度 \(z_{occ}\) 就作为 \(d_{Blocker}\)。

如下图5X5的采样结果，若设 \(d_{Receiver}\) 为7，那么平均遮挡深度 \(z_{occ}\) 则为红色部分的平均值。

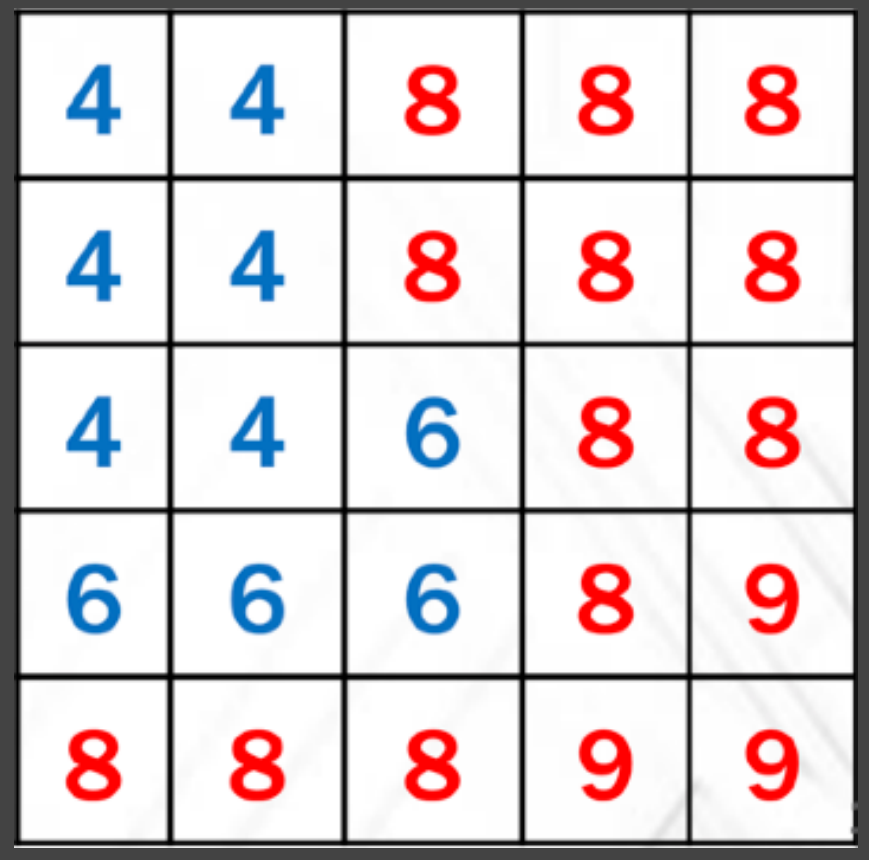
设该采样范围的面积为 \(N\)，无遮挡的面积占有 \(N_1\)，有遮挡的面积则占有 \(N_2 = 1-N_1\) ，则有：

\[\frac{N_{1}}{N} z_{\text {unocc }}+\frac{N_{2}}{N} z_{o c c}=z_{A v g} \]

我们做出两个假设：

• 假设深度分布为正态分布。无遮挡率则为：

  \[P_1(x>d_{Receiver}) = \frac{N_1}{N} \]

• 假设绝大部分没被遮挡的情况都属于同一个深度（相当于在同一个垂直于光方向的平面）​ ：

  \[z_{unocc} = d_{Receiver} \]

那么 Blocker Search 算法的公式表示为：

\[d_{Blocker} = z_{occ} = \frac{N\cdot z_{Avg} - N_1 \cdot z_{unocc}}{N_2} = \frac{E(x)-P_1(x>d_{Receiver})\cdot d_{Receiver}}{1-P_1(x>d_{Receiver})} \]

再利用切比雪夫不等式加速求解 \(P_1(x>d_{Receiver})\) 即可。

注：\(P_1\) 是在范围为 \(w_{blockersearch} * w_{blockersearch}\) 下的概率估计。

加速 PCF 算法

PCF 算法中的多重采样：每次采样得到的遮挡物深度用来与 \(z'\) 做大小比较（小于 \(z'\) 则视为被遮挡，大于 \(z'\) 则视为全亮），最后取比较结果的平均作为 Visibility。

我们做出一个假设：

• 假设深度分布为正态分布。无遮挡率为：

  \[P_2(x > z') \]

那么 PCF 算法的公式表示为：

\[Visibility = P_2(x>z') \cdot 1 + (1-P_2(x>z')) \cdot 0 = P_2(x>z') \]

再利用切比雪夫不等式加速求解 \(P(x>z^{'})\) 即可。

注：虽然 \(z'\) 和 \(d_{Receiver}\) 是一样的，但 \(P_2\) 是在范围为 \(w_{\text {Penumbra }}*w_{\text {Penumbra }}\)下的概率估计，与 \(P_1\) 不同；在利用切比雪夫不等式求解时，\(P_1\) 和 \(P_2\) 需要分别在不同的层级采样 mipmap。

VSSM 的缺陷

VSSM 的主要缺陷表现：

• 并不是任何深度的分布都是符合正态分布模型的，例如对于图右的简单几何体反而用正态分布表示会很不适合。

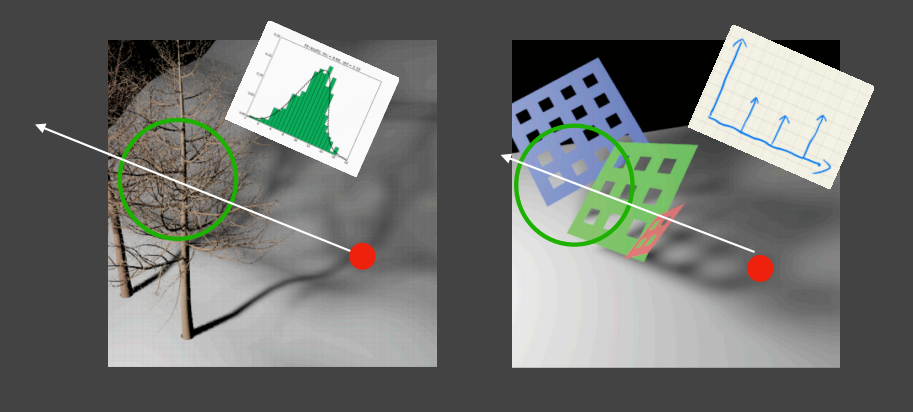
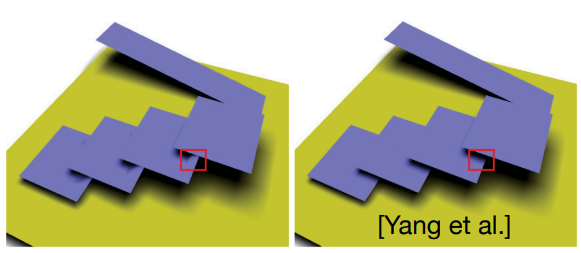
• 漏光（Light Leaking）现象，在一些应当被阴影完全遮蔽的内部有可能仍产生亮度。

• 在加速 Blocker Search 算法中的假设 \(z_{unocc} = d_{Receiver}\) 基于认为绝大部分没被遮挡的情况都属于同一个深度，但实际上有些不被遮挡的地方深度并不等于 \(d_{Receiver}\) 。

Moment Shadow Mapping（MSM）

Moment Shadow Mapping 正是为了解决 VSSM 缺陷的一种算法，它主要想法是：使用高阶的矩去描述一个分布的 CDF。这样就能通过记录 m 阶的矩，就能复原成足够接近实际 CDF 函数的效果，从而能适应不同的深度分布模型（有些地方可能接近正态分布，有些地方可能奇奇怪怪的分布）。

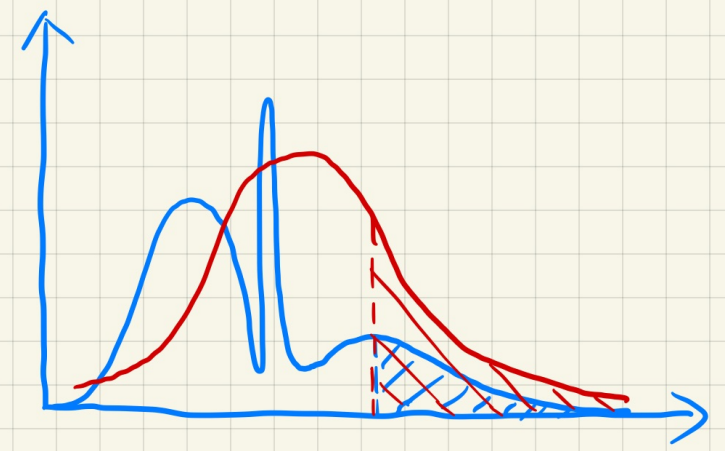
Moment Shadow Mapping将使用最简单的形式来标识矩：\(z,z^2,z^3,z^4,...\)

实际上，VSSM 本质便是记录 2 阶的矩来复原 CDF 函数，而 Moment Shadow Mapping 一般使用4阶的矩就已经足够接近实际 CDF 了。

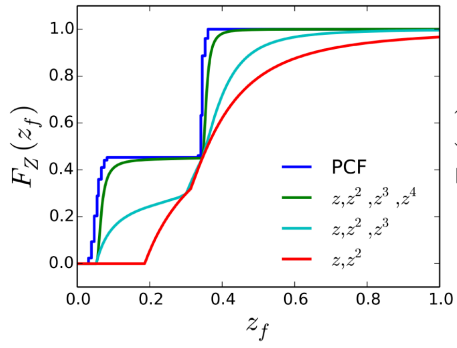
虽然 Moment Shadow Mapping 效果相当不错，很好的解决了 VSSM 绝大部分缺陷，但是它仍需要相当的额外空间开销和重建矩的额外性能开销。

Exponential Shadow Mapping（ESM）

ESM 主要是为了实现硬阴影的边缘软化和避免锯齿（类似 PCF），但 PCF 是无法实现 pre-filter 的，而 ESM 可以。

而 pre-filter 的最大的好处是，如果项目采用的技术框架是 precomputed shadow map，那么就可以换成 precomputed exponential shadow map，无任何额外开销还能顺便实现了边缘的软化。

ESM 的核心思路在于将传统的阴影测试函数：

\[s(d, z)= \begin{cases}0 & d>z \\ 1 & d \leq z\end{cases} \]

\(d\) 为 shading point 在 shadow map space 的深度，\(z\) 为 shadow depth。

替换成指数函数的形式：

\[\begin{aligned} f(d, z) & =e^{-c(d-z)} \\ & =e^{-c d} e^{c z} . \end{aligned} \]

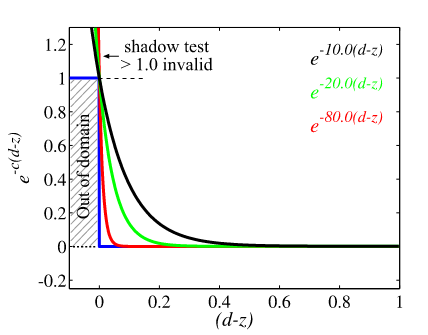
这两种函数的可视化如图所示，并且 \(c\) 越大指数函数会越接近阴影测试函数：

在具体效果上，\(c\) 越大，那么阴影效果会越硬；反之会越软。

而 PCF 的滤波计算如下：

\[s^{\prime}(d, z)=\sum_i^N w s\left(d, z_i\right) \]

而 ESM 的滤波计算则如下：

\[\begin{aligned} f^{\prime}(d, z) &=\sum_i^N w f\left(d, z_i\right) \\ &= \sum_i^N w e^{-c d} e^{c z_i} \\ &= e^{-c d} \sum_i^N w e^{c z_i} \end{aligned} \]

可以看到因为传统阴影测试函数会把 \(d\) 和 \(z\) 耦合在一起，因此 PCF 的滤波计算无法将它们拆离开来；而 ESM 则可以分离 \(d\) 和 \(z\) ，从而单独对 \(z\) 这部分进行预滤波，并将该结果存进 ESM 纹理中（只需一个通道）。

Log 空间存储

另外，ESM 如果直接存储滤波结果可能会有较大精度损失，因此一种改进是存储 log 空间的结果，这样就能大大提升精度：

\[\begin{aligned} \ln \left(result\right) &= \ln \left[\sum_{i=0}^N w_i e^{c z_i}\right] \\ &=c z_0+\ln \left[w_0+\sum_{i=1}^N w_i e^{c\left(z_i-z_0\right)}\right] \end{aligned} \]

在实践中，通过 log 空间来进一步提升精度，在深度变化不大的区域看起来效果不错，然而深度变化较大的区域仍然会出现浮点数溢出，从而产生明显的 artifact。因此在实践时还需要结合一些手段避免浮点数溢出问题。

Exponential Variance Shadow Map（EVSM）

回想一下 VSSM 的漏光问题，其常见于多层遮挡物重叠的情况。

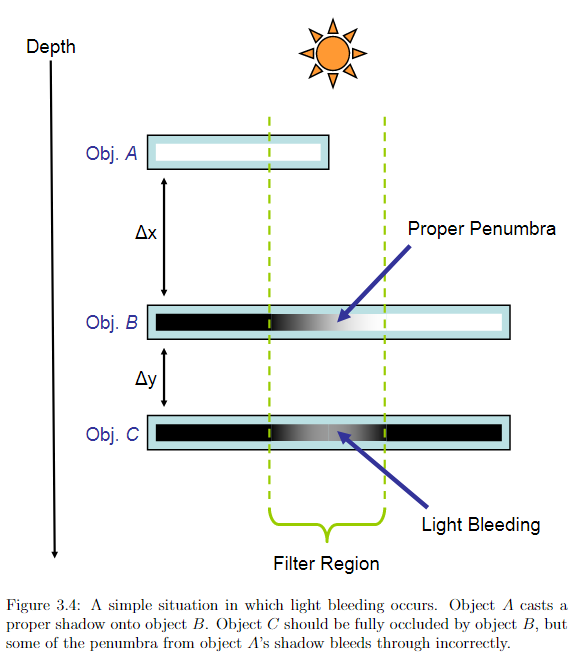
如下图三个物体A、B、C（对应的深度记为a、b、c），由于 light space 下只记录最前面的深度即 a 和 b，该段滤波区域的方差只受 \(\Delta x=b-a\) 控制（均值也只受 a 和 b 控制），与 c 无关；理论上 c 的 cdf 只占据了正态分布曲线的尾部面积，则 c 会得到一个接近于完全遮蔽的值（虽然 ground truth 上应当是完全遮蔽），然而当 c 比较靠近 b 时（\(\Delta y = c-b\) 较小时），c 占据的尾部面积会变得很大，以至于出现较亮的漏光现象。

综上，我们希望抑制漏光现象，就得减少 \(\frac{\Delta{x}}{\Delta{y}}\) 这个比例。

在前人的工作中发现，深度本身可以用一个函数包装（该函数称为 warp function），然后阴影算法（无论是传统 shadow map 还是 vssm）全按 warp 后的结果来计算也会得到正确的阴影结果（只是阴影可能呈现的效果稍微不同）。

函数只要在非负数域内维持单调不减性就可以用于 warp。

而 EVSM 的作者受 ESM 启发，在 VSSM 的基础上使用了这个 warp function：

\[f(z) = e^{kz} \]

结果就是 \(\frac{\Delta{x}}{\Delta{y}}\) 比例就降低了；并且常数 k 越大，这个比例就越低，从而漏光现象就更少，但是也可能导致另一种 artfact：在非平面或多个 receivers 的效果不正确。因此作者又额外使用了另一个曲线更缓和的 warp function：

\[f(z) = -e^{-kz} \]

在计算阴影时，对这两种 warp function 分别使用切比雪夫不等式求出各自的 visibility 值，并取这两个值的 min 值作为最终 visibility 值，这样就可以修复大部分 EVSM 的 artifact。这也意味着，EVSM 需要记录 \(e^{kz}\),\(e^{2kz}\),\(-e^{-kz}\),\(e^{-2kz}\) 四个通道的值，性能比 VSSM 还要更费。

原文提到，当出现 VSSM 和 ESM 共有的 artifact 时，采用了两种 warp function 的 EVSM 才会有 artifact。

总的来说，该方法还是不适宜落地，虽然能够解决大部分 VSSM 的漏光问题，但性能开销还是略高，并且也和 ESM 一样存在数值精度的问题。但是其核心思想可以提炼一下：深度本身就是某种函数表示，将物体的远近关系用非线性的关系表达出来。因此用 warp function 实际上就是在将物体的远近关系进行重新表达，不同的 warp function 有不同的作用，例如可以将远近关系更加凸显的指数函数。

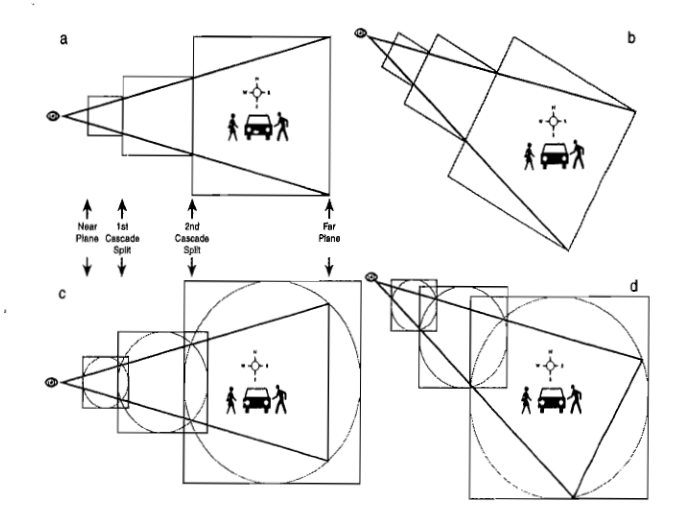
Cascade Shadow Map（CSM）

当 Shadow Mapping 应用在大型场景中时，一张正常分辨率大小（如1024×1024）的贴图用来记录整个大型场景的阴影深度信息是非常不精确的，尤其是在靠近主摄像机的地方所看到的阴影将是严重失真的（一块块栅格）。

Cascade Shadow Map（CSM） 借鉴了 LOD 的思想，对主摄像机的视锥体范围进行了划分，然后对每个划分区域采用相同分辨率大小的 Shadow Map，这意味着：离主摄像机比较近的地方往往区域面积是比较小的，这样 Shadow Map 能够表示的深度信息就更精确些，看到的阴影效果也更真实；离主摄像机比较远的地方往往区域面积是比较大的，虽然使用相同分辨率的 Shadow Map 能够表示的深度信息比较不精确，但对于远处的物体来说，这种不准确是可以接受的。

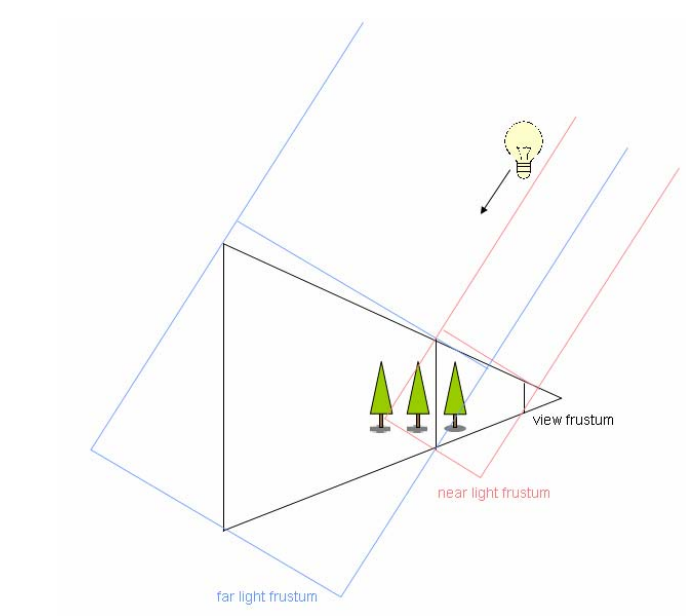
CSM 的代价很明显，即划分了多少层区域，就要使用多少倍数量的 Shadow Map；但 CSM 已经算是比较廉价且视觉效果不错的大型场景 Shadow 解决方案，在工业界得到广泛应用。

CSM（一层Shadow Map）的效果：

CSM（三层Shadow Map）的效果：

视锥分割

首先需要对视锥体划分成若干层（每一层在主摄像机观察空间下的 z值范围 分别从哪到哪），有如下方法：

• 通过自定义比例来分割

• 通过对数比例分割：这是较理想的比例公式，能够减少 Shadow Perspective Alias 问题的出现（下面是公式推理的内容）。

Shadow Perspective Alias：透视投影会产生近大远小的效果，可能会让近处物体的多个像素对应着 Shadow Map 中的一个纹素，从而产生 Alias。

假设，\(dp\) 为主摄像机近平面上的一小段距离， \(ds\) 为 ShadowMap 平面上的一小段距离。

通过下图的分析，通过几何关系容易得：

\[\frac{dp}{ds} = \frac{n\tan(\theta)dz}{z}/ ds \]

\(\varphi\) 和 \(\theta\) 为物体平面法线的角度参数，则 \(\tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}=\frac{\cos(\varphi)}{\cos(\theta)}\)

\(n\) 为主摄像机近平面距离，\(f\) 为主摄像机远平面距离。

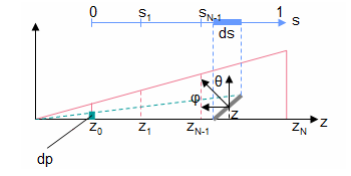
我们期望各层 Shadow Map 的投影和主摄像机图像分辨率都呈现尽量相同的比例（即比例与 \(z\) 无关）：

\[\frac{dp}{ds} = C_0 \]

接着，我们假设所有物体表面法线都是一样的，也就是说 \(tan(\theta)\) 也将是一个常数。

这个假设是针对这类物体：一个横跨了多层 Shadow Map 具有相同朝向的物体（如一长块墙面），在各层 Shadow Map 交界处很容易被看出边界的artifact问题（上下两层 Shadow Map 精准度不同）。

最终整理得到这么一个式子：

\[\frac{1}{z}\frac{dz}{ds} = C \]

解一下微分方程得：

\[z=n \cdot \left(\frac{f}{n}\right)^{s} \]

分别代入 \(z=n,s=0\) 和 \(z=f,s=1\) 解得。

最终，把若干层 Shadow Map 视为若干段 \(s\)，代入得：

\[z_i=n \cdot (\frac{f}{n})^{\frac{i}{N}},i=1,...,N \]

但是对数分割是一种理论上的理想分割，在场景物体从近到远分布均匀的情况下才有比较好的表现，而在实际应用中是很少出现以上理想情况的。因为使用对数比例计算出来的一层 CSM 通常距离很小，在多数情况下都是比较空旷的，这就造成了大量的浪费。

因此通常会与线性分割进行一个混合，公式如下:

\[z_{i}=\operatorname{lerp}\left(n *(\frac{f}{n})^{\frac{i}{N}}, n+\frac{i*(f-n)}{N}, \lambda\right), i=1, \ldots, N \ , \lambda \in [0,1] \]

\(\lambda\) 是一个 \([0,1]\) 区间的控制参数，用以在对数和线性之间进行插值

计算包围盒

分割好各层视锥体后，我们需要选择对应的 Shadow Map 来恰好包围住视锥体（即各层的 Light Camera 的光锥体刚好包围住视锥体）。

有如下做法：

• 使用最紧凑的方形包围盒：分割后的视锥体的8个顶点在世界空间上做的View变换后，取它们最大最小x值y值z值来作为 Light Camera 的远近平面参数设置。

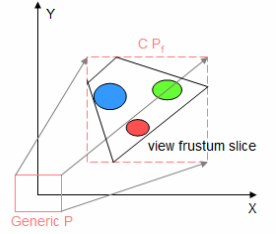
然而这种做法很容易导致远近平面大小频繁变化，在视锥体发生变化的情况下容易出现阴影边缘闪烁的瑕疵（shimmering edge effect or shadow flickering）

• 使用固定的最大方形包围：既然频繁变化容易导致阴影抖动，那么就干脆使用一个固定的最大方形包围盒来包围任意角度下的视锥体。代价则是会包含有更多视锥体以外的位置，降低了Shadow Map的利用率。

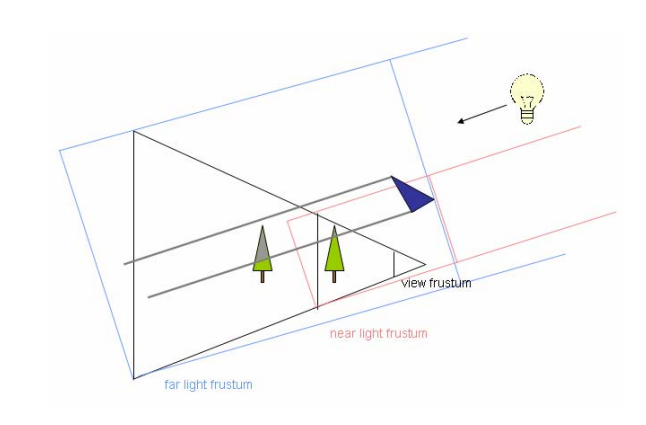
此外，还有使用球形包围盒的方法来构造光源正交矩阵，优势是可以通过很低廉的算法来进行层级选择：即像素点坐标到球心的距离与半径比较。

层级选择

有了若干层 Shadow Map 后，渲染某个shading poing时该如何判断点在哪个层级：

• 直接通过视锥分割的z值范围来判断所在是哪个层级

• 通过各层 Light Camera 的 View 变换和 Projection 变换，得到点在该层 Shadow Map 的 UV 坐标，当 UV 坐标在 [0,1] 范围内时则说明在该层级内

前面我们在视锥分割已经确定了z值划分范围，直接简单根据shading point的z值来判断层级不是更好吗？这是因为每一层的 Shadow Map 其实多多少少包含了更远一层的部分阴影信息，但是它的精准度明显要比更远层的 Shadow Map 要好，因此通过uv坐标判断点所属层，就可以尽量命中较近层的 Shadow Map。

不过，如果仅选择单个层级，会容易出现各层级阴影交界处出现阴影效果剧变的问题，这时候也可以混合上下两层 Shadow Map 来让交界可以过渡变化。

分帧更新

每帧绘制所有层级的 shadow map 可能会性能开销大，因此我们可以对远处阴影的 shadow map 进行更低频率的更新：对于高层级的 shadow map，我们不必要每帧都更新，而是可以每 n 帧重新绘制一次。

Stablize CSM

由于 CSM 的阴影矩阵是随视锥体变化而变化的，而矩阵的数值精度问题可能会导致阴影计算的结果产生抖动。Stablize CSM 会将相机的变化拆解为旋转和平移。

视锥体旋转时，stablize CSM 会对视锥切割部分建立一个固定大小的圆形包围盒（如图 c），这样无论视锥体如何旋转，切割部分都不会超出其所在的包围盒；接着，我们就对圆形包围盒建立 AABB，该 AABB 将作为 light camera 的远平面。因为该 AABB 的大小也同样是固定大小，并且 AABB 并不会和 OBB 那样随意旋转，因此 stablize CSM 的阴影矩阵就不会每帧产生新的旋转，而只会转化成平移并叠加上相机的平移。

而对于平移部分就更简单了，就是说平移后的位置是一个任意的数值（基本上会带各种小数），而小数部分就会存在精度误差。而我们只要让平移后的位置对齐到整数，这样就可以当相邻两帧平移矩阵发生变化时，避免了小数部分带来的精度误差。

Virtual Shadow Map

与 virtual texture 相似，假设存在有一张超巨大的 shadow map 覆盖了超大范围的场景，这张巨大的 shadow map 称之为 virtual shadow map；然后根据 camera 所可见的范围来将 virtual shadow map 划分出所需要访问的块（实际在术语上，更多会称之为页，即 page），一个 page 可以是例如 128×128 分辨率的纹理块。

根据访问请求，去 page table 中查找有没有存在对应的有效 physical page ：

• 如果有，则直接访问该 physical page。
• 如果没有，则意味着发生 page fault（缺页错误），需要后续进行一定操作来得到对应的 physical page 以供访问。

但与 virtual texture 不同的是：page fault 的时候不用从内存/硬盘中把对应 page 换入到显存，而是直接在管理机制分配得到的 unused physcial page 上重新进行物体的绘制来生成该 page 上的 shadow depth 信息。

这样设计的原因是考虑 I/O 开销远远比重新生成深度的开销要大。

这也就意味着，VSM 是不需要两级存储之间的换入换出，而仅需要使用显存作为物理存储。

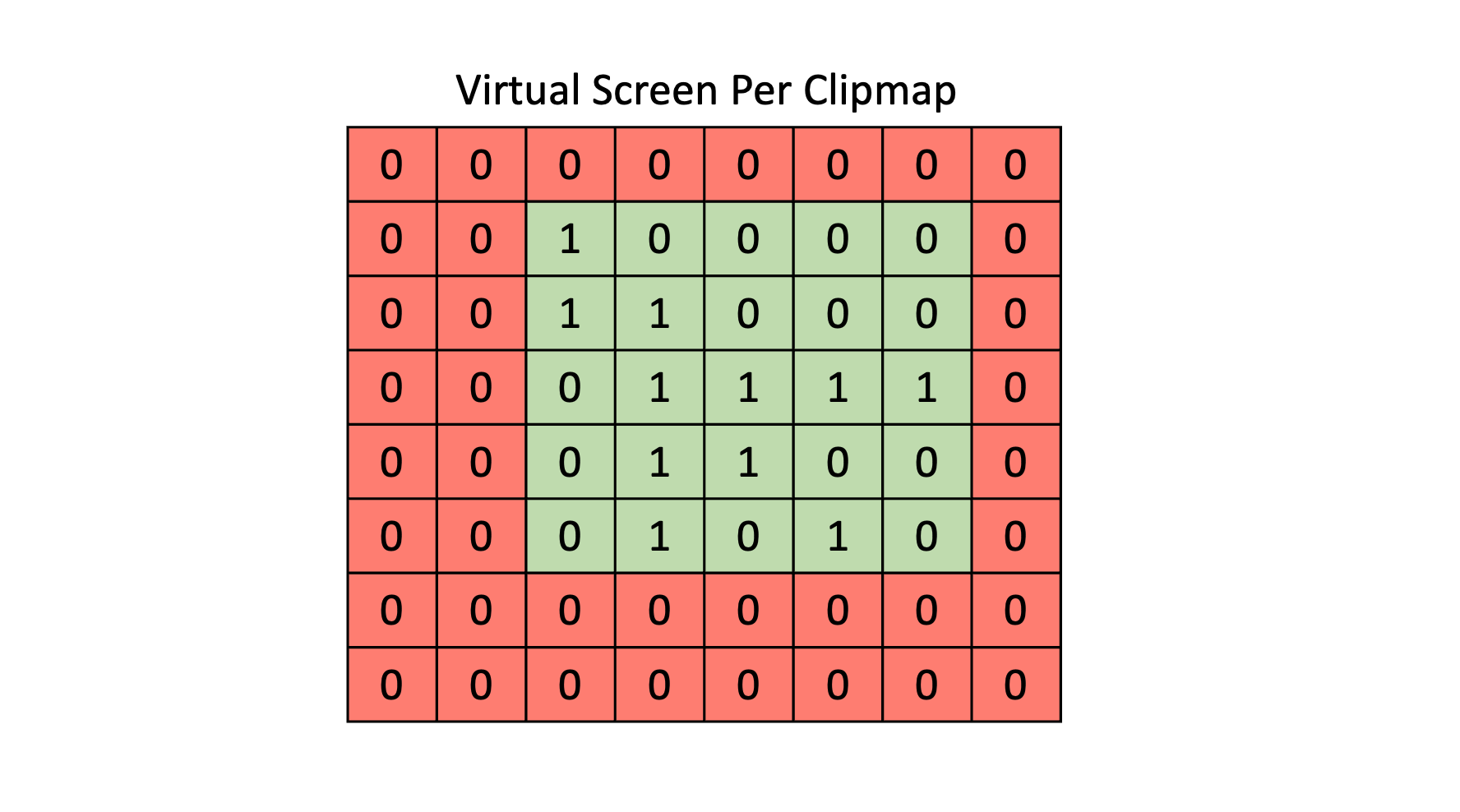
Clipmaps

VSM 往往采用了 clipmap 的设计来实现摄像机近处阴影高精度、远处阴影低精度的效果。在具体实现上，一般是用 6 层 clipmaps，每层 clipmap 均为 8k×8k 分辨率的 virtual shadow map，然后这些 clipmaps 共享一个物理内存池分配。

这就意味着，我们的 virtual pages 总数将共计有 \(6×(8k×8k)÷(128×128)=24576\) 个，而实际上 physical pages 的总数则取决于我们的控制：如果 physical pages 总数多一些，那么物理内存池的显存占用明显变大，但同时也会更少出现 page fault。

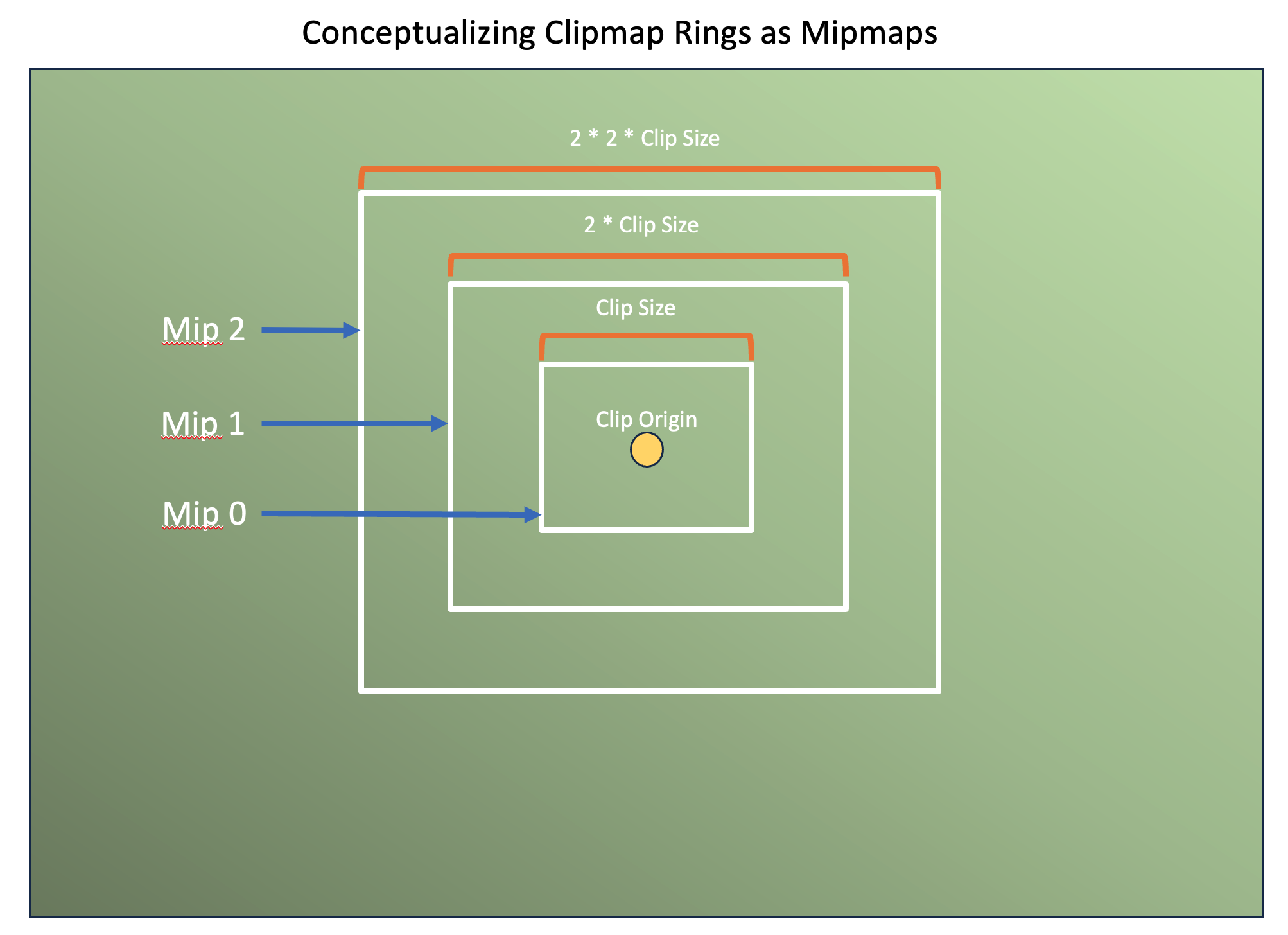
并且由于采用了 clipmap 设计，我们可以利用文章后面的 shadow cache 技术来进一步优化 VSM。

稀疏内存管理

由于 virtual shadow map 是需要将物理内存划分为一块块 page 来按需分配，也就是需要稀疏内存（sparse memory）管理机制。这里大概有两类方式实现：

• 软件实现：在 GPU 上提前分配一个固定大小的巨大物理内存池（常见于 texture2D array 或者一张巨大的 altlas），并通过一些 compute shader passes 来管理这块物理内存块的 physical pages 分配。缺点是占据的显存一直都会这么多，并不会动态伸缩；并且往往不能方便支持硬件的深度写入，而是得软件实现 shadow depth 写入，更具体原因可见后续算法过程。

一般情况下我们会推荐使用 texture2D array，原因如下：

• 当使用 bilinear sampler 去采样 atlas 时，采样到边界是会混合了相邻 page 的 texels，这往往会造成边界突变问题，因此需要正确使用 atlas 就得让 page 扩边 1 个单位（例如 127×127 分辨率扩边成 128×128 分辨率），并且还得对扩充的边界进行数据填充。而 texture2D array 是不会存在这样的问题。
• texture2D array 的一个 layer 就代表了一张 page 及一系列由其生成的 mipmap，可以很方便支持实现 VSM 的软阴影效果。

UE5 VSM 便是采用了 texture2D array，共有 4096 个 layers，其一个 mipmap level 0 的 page 就为 128×128 分辨率。

• GPU 硬件/API 支持：如果硬件/API 支持稀疏内存分配机制，例如：Sparse Textures OpenGL、Sparse Resources Vulkan、Tiled Resources DirectX。那么这种方式可以减少内存管理的工作量，并且也能有更合理的显存占用（不用预先分配）。然而支持该特性的机器少之又少，并且特性本身也还不成熟（现在还有一些 issues 报告 sparse texture 性能差的问题）。

算法过程

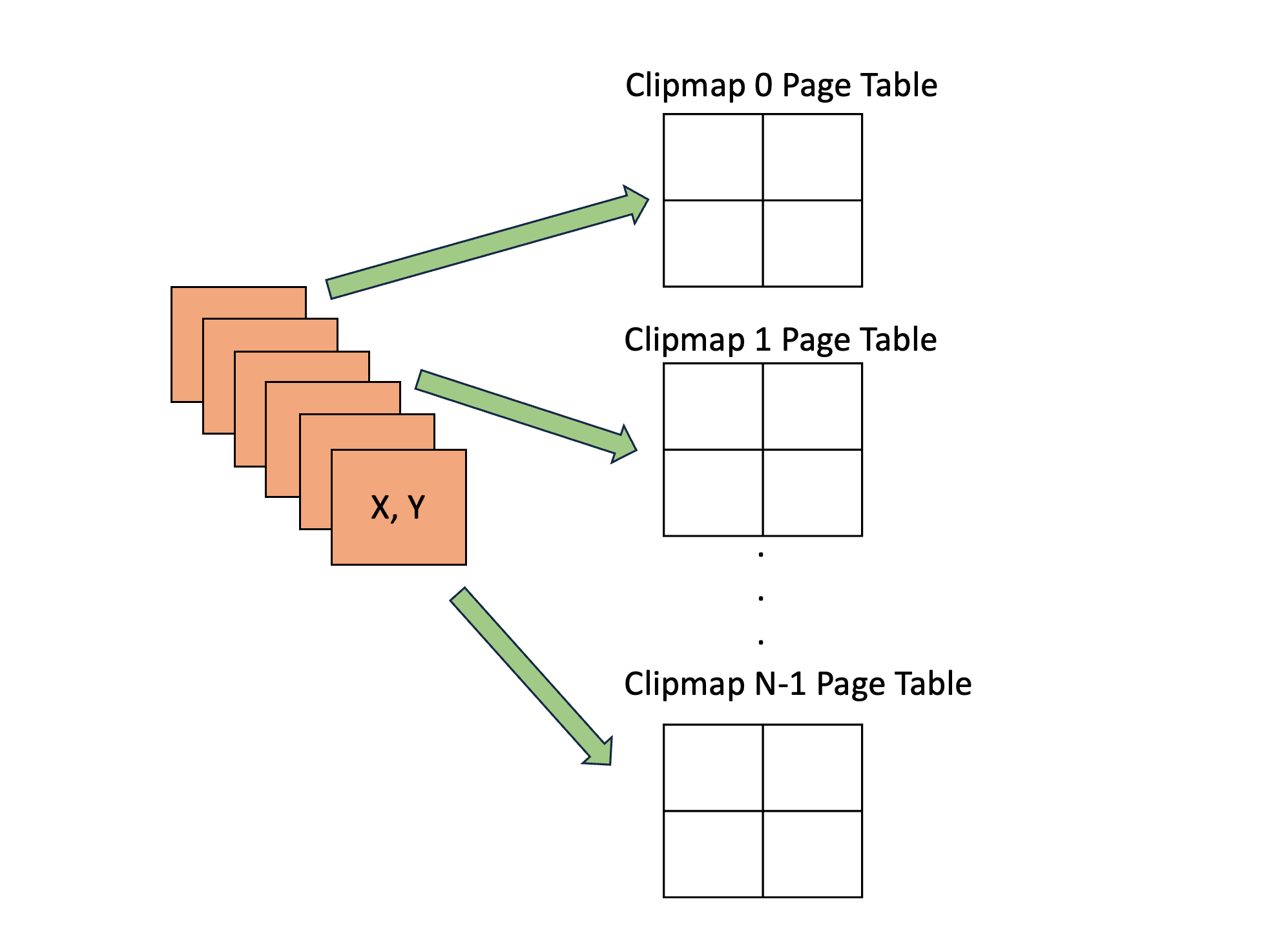
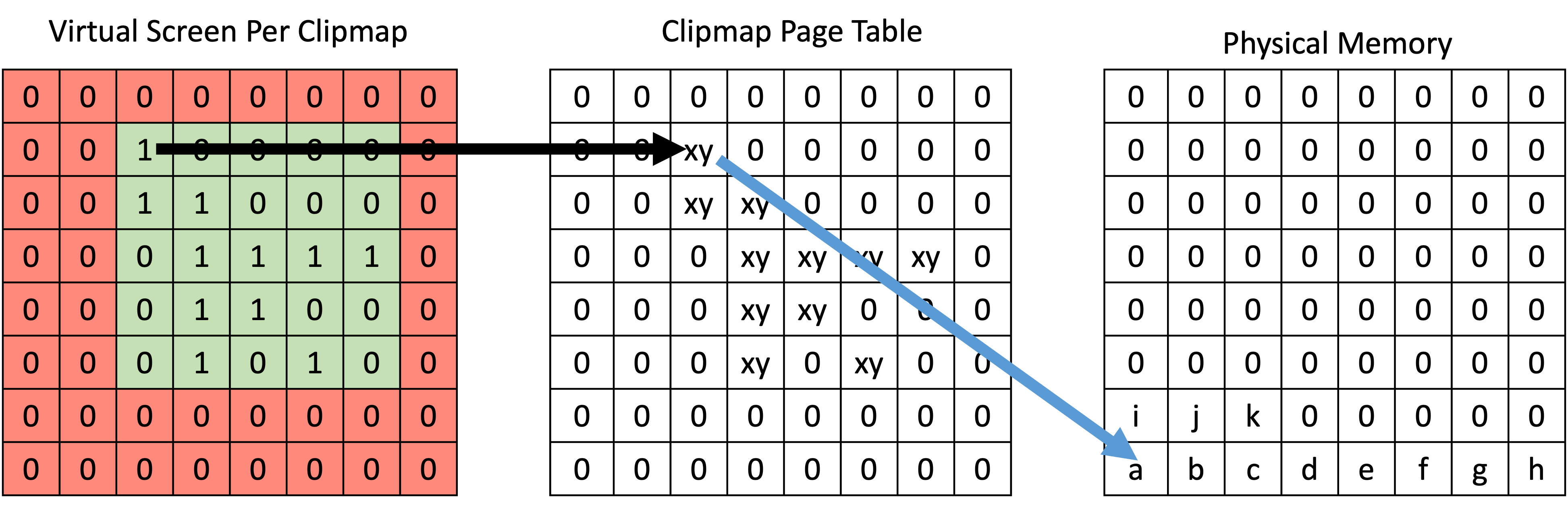
1. Analyze Depth：对每个 screen pixel 从 world space 转换成 light space 再转换成 virtual shadow map space（实际上就是当前的 clipmap space）的坐标 (x,y)，并在 page table 里找到对应的 page entry 项（注意不是找到对应的 page），标记该 page entry 的 frame marker 为 1（代表着本帧将要访问该 page）。

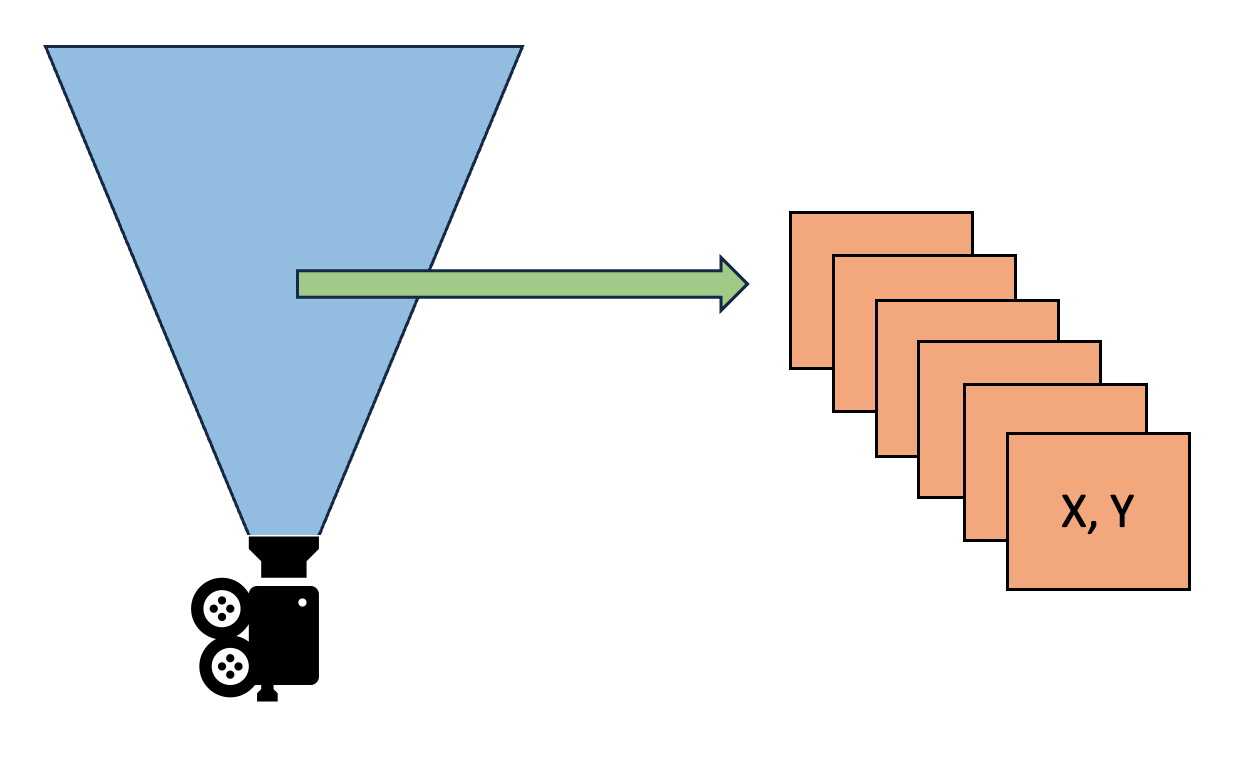
page entry 可以理解为一个 virtual page 和 physical page 的映射关系，其还包含了本帧是否要访问该 page 的状态（frame marker）、physics page 位置（X,Y,pool index）、physics page 是否有效（Residency Status）、是否需要重新生成（valid/dirty status）等属性。

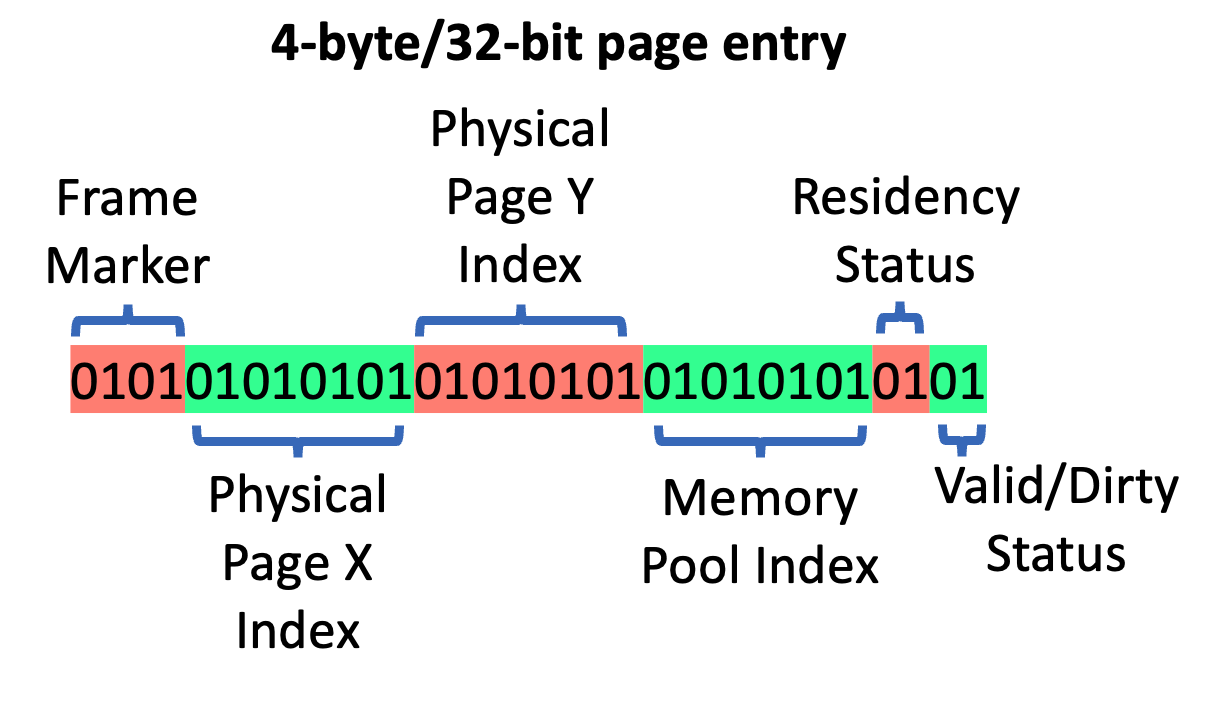
frame marker 的最低位 0 表示本帧没有被访问，1表示本帧将要被访问；而前面的几个位则分别表示前第几帧是否被访问。这样设计 frame marker 的原因是为了稍微延长一下该 page 的生命周期，避免产生频繁的 page 重复分配/释放。

2. Consult Page Tables：遍历 page table 里的所有 page entries，并判断 page entry 对应的 page 是否无效，如果无效则视为产生了 page fault（page entry 也被标记为 dirty）。

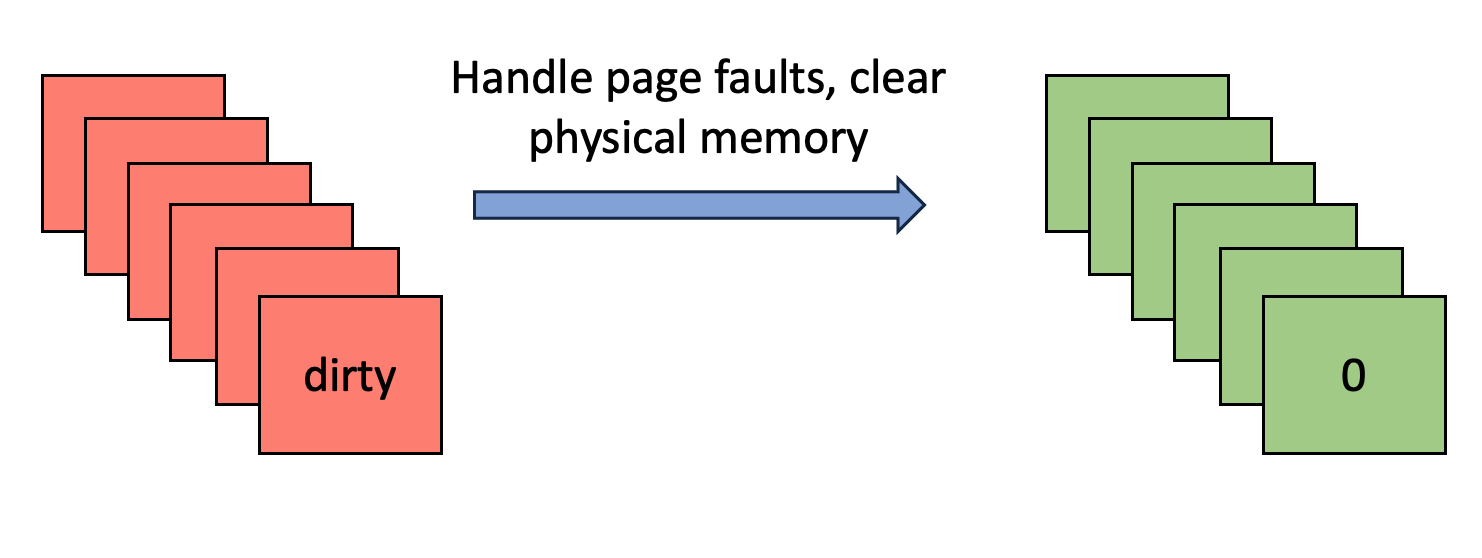
3. Handle Page Faults：对所有 dirty page entries 进行处理：
   • 如果不存在对应的 physical page，那么为其分配新的 physical page，并进行清 0 操作。
   • 如果存在对应的 physical page 但只是数据过期了，则直接进行清 0 操作。

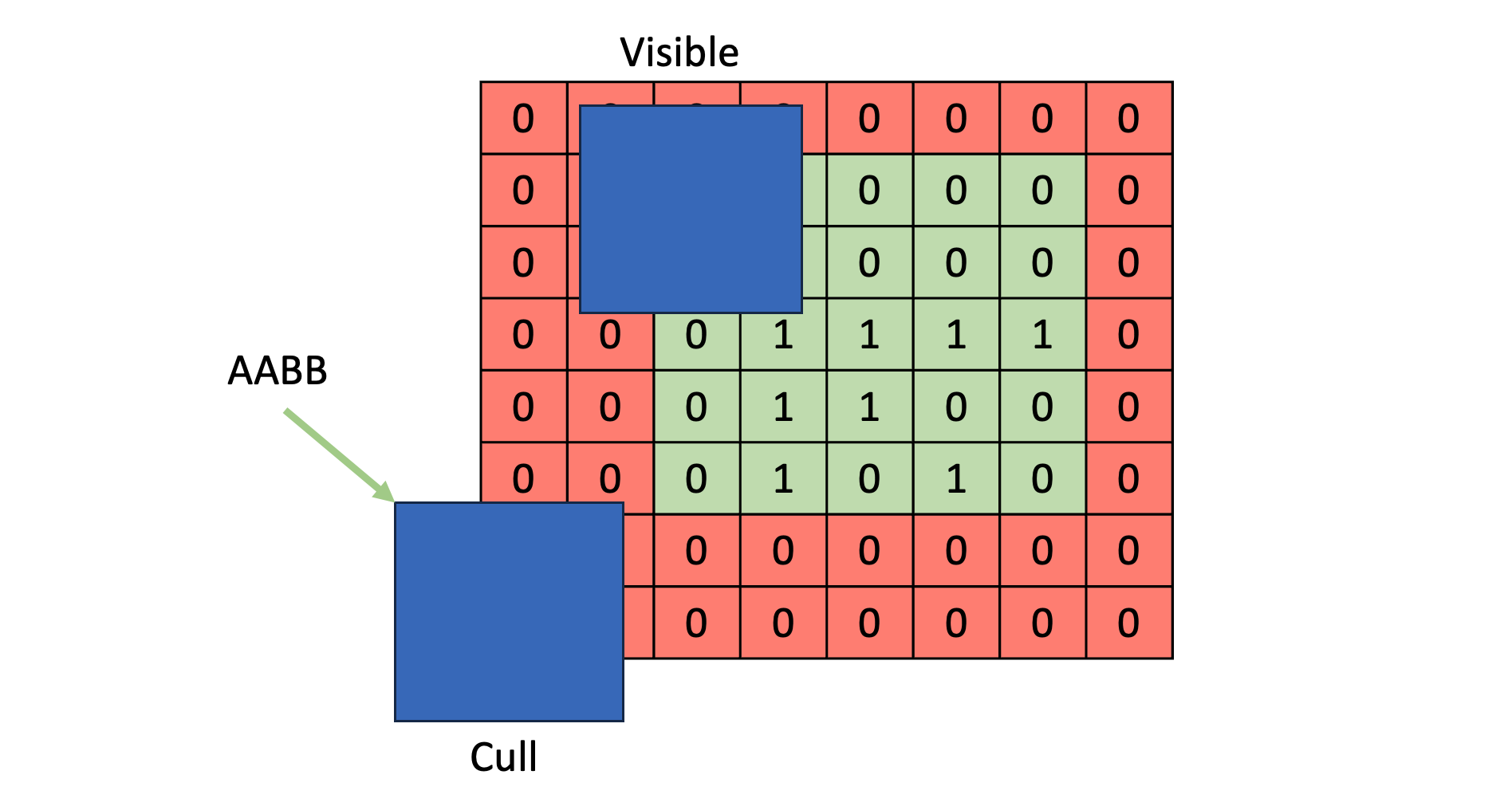
4. Cull Objects：在 virtual shadow map space（当前 clipmap space）下，我们已经知道了各个 dirty page 的位置。那么我们需要算出一个 AABB 刚好围住所有 dirty pages，并且称之为 screen bounds。

   如图，page 标记为 1 意味着该 page 是 dirty page，是需要重新生成 shadow depth。当前 clipmap 范围为红色区域，而 screen bounds 范围为绿色区域。

   

   将不需要的物体剔除掉，剔除手法包含但不限于：

   • objects 的 AABB 与 screen bounds 的相交测试。
   • objects 之间的遮挡剔除。
   • objects 的 AABB 与各个 dirty page bounds 的相交测试。

UE5 则可以利用基于 nanite 的 instancing culling 和 cluster culling，这种基于 GPU driven 的 culling 会。当然，文章后面的 shadow caster culling 技巧也能结合于此。

5. Render To Physical Memory：对剔除后的物体进行绘制，将 shadow depth 写入到对应 page 中的对应位置。当我们采用软件实现的稀疏内存管理机制时，由于同一个三角形光栅化形成的 fragments 有可能属于不同的 pages，我们需要在 fragment shader 里查 page table 来得到 physical address 后，才能写入 shadow depth。这就意味着：
   • 我们不能依靠 z-test 写入或者 render target 写入，而只能对 image UAV 的进行 atomic min/max。因此 shadow depth 得用 unit32 而非 float 来表示。
   • 丧失了硬件的 early-z test 优化。

当然这种方法也可能导致一定的性能问题：大量生成的 fragments 在 fragment shader 查表后发现自己映射在 vaild page 上就直接 discard 了。也就是说 view port 设为 screen bounds 时很可能会产生很多不必要的 fragments。

也可能有人认为，为什么不以 dirty page 为 viewport 进行绘制 ？以 dirty page 为 viewport，就可以在 vertex shader 中进行重映射操作，不仅能利用硬件深度测了，并且还能避免所有没必要的 fragments 生成，但是与此带来的缺点是绘制的次数很可能会多很多（因为最坏情况下，有几个 dirty pages 就意味着有几个 viewports，从而就得绘制几遍所有物体）。

因此可以考虑一种兼顾的方案是，将 screen bounds 内以 n×n pages（例如 n 为 2）为一个 viewport 来进行绘制，但如果 n×n pages 里没有任何 dirty page 时就不会进行。虽然还是不能利用用硬件深度测试写入，但是已经能避免相当部分没必要的 fragments 生成。

VSM 是一套比较新的 GPU driven shadow map 方案，主要是在工程实现上比较复杂，还有更多实现上的细节和优化空间值得再开一篇博客剖析，但是篇幅有限就不多展开。

Per Object Shadow

当需要物体产生高精度的阴影时，就可以单独对物体生成 per object shadow，放在 shadow map 外的另一张 texture。为了避免生成多张 textures，这些 per object shadows 都会塞进同一张 atlas，通过 uv min 和 uv max 确定某个 per object shadow 的范围。

per object shadow 常见于角色阴影，并且还可以用于做多光源下的角色阴影。图来自于【星铁】截帧浅析 - 知乎 (zhihu.com)。

生成好 per object shadows 后，还得考虑下一个问题：不可能每个 pixel 都要读 shadow map + 所有 per object shadows，这会导致极大的带宽开销。因此需要尽可能减少不必要的 shadow reading。

一个 naive 的想法可能是在 CPU 判断物体与哪些阴影体积相交来决定物体在绘制时需要读取哪些 per object shadow，但是很费时且粒度过大！因此可以考虑以下内容。

自阴影

物体阴影基本都会有一定阴影投射到自己身上，因此用于生成 per object shadow 的物体必须要读取自身的 shadow。

结合 Shadow Volume 技术

对 object 建立 shadow volume 并进行绘制，启动深度比较但关闭深度写入，并在 fragment shader 中加入了读取 per object shadow 并判断是否遮蔽，并将结果写入到一张 screen space shadow mask texture 中。

shadow volume 往往是 light space 下对 object 建立 AABB 后再往光源方向延长成的体积。shadow volume 相关技术更具体可以看实时阴影技术系列的第（2）篇，其中有更详细的介绍。

screen space shadow texture 实际上也可以是一个 8 bit stencil buffer 或者 g-buffer 中某个通道之类的。并且还可以根据需要定制，不一定得写入单一光源的 shadow mask，例如可以是：

• 多个光源的 shadow masks，8 bit stencil buffer 就能表示 8 个光源的阴影。
• 单个光源的 shadow factor。

并且在同一光源下，多个 object 各自所产生的 shadow volumes 是可以进行 batching 的，即 1 个 draw call 完成。

此外，绘制 shadow volumes 也应该开启 early stencil test 来避免 shadow volumes 重叠而产生的 overdraw。

延迟阴影管线

正常的 shading pass 往往是包含计算光照和阴影，而延迟阴影意在将计算光照和计算阴影分离：先计算阴影的遮蔽率后将 shadow mask 写入到一张 screen space shadow texture 后，在后续进行着色时读取 shadow mask 并将遮蔽率与着色结果相乘。

为啥要分离阴影计算和光照计算呢？个人认为的好处有如下：

• UE 中的 modulated shadow（即对应于 per object shadow）没有采用延迟阴影，而是在绘制 shadow volume 的 fragment shader 中（计算阴影时）就直接将 scene color 乘上 shadow factor，因此可能导致如图的重复混合错误。

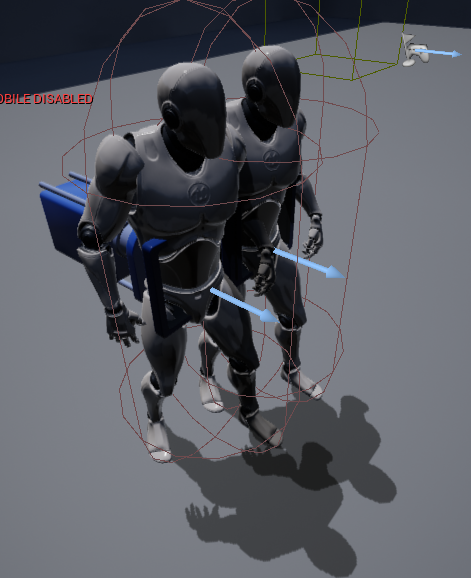
• 如果光照着色采用的是 draw light volume 形式，可以通过 early stencil test（假设 shadow mask 写入到 stencil buffer 中）来避免阴影区域 fragments 的光照计算。

Shadow Caster Culling [预计算]

Shadow Caster & Shadow Receiver

Shadow Caster：产生阴影的物体

Shadow Recevier：接受阴影的物体

• 手动/自动设置非 caster 物体（减少 shadow map draw call）：如最底下的平地。

• 手动/自动设置非 receiver 物体（减少 read shadow map）：如必定不会被阴影遮蔽的某块区域。

• 部分 casters 可以使用低模代理（shadow proxy），减少 draw call 的顶点数。

  如角色可使用 capsule shadow（胶囊体阴影）。

Precomputed Shadows

• 预计算：针对静态物体预生成一张 precomputed shadow map，并存储在硬盘上；需要的时候 upload 到 GPU 里。

  可利用 direct storage 之类的硬件特性支持来优化。

• 运行时只对动态物体 draw call，生成另一张 dynamic shadow map。

  如果两张 shadow map 占用空间太大，可以考虑 precomputed shadow map 搭配 per object shadow。

• precomputed shadow map 的压缩方法：不展开，可参考 shadowmap压缩 - 知乎 (zhihu.com)

PVS（Potential Visible Set）

• 预计算：预先计算生成出每个区域的潜在 casters 列表，并存储在硬盘上。
• 运行时：根据玩家走到某个区域，获取对应的 casters 列表来用于调用 draw call 并生成 shadow map。

Shadow Caster Culling [运行时]

Shadow Map Caching [2012]

往往需要两张 shadow map，可以称为 cached shadow map 和最后真正要用的 temporary shadow map。其思想和 precomputed shadow 类似，只不过 cached shadow map 并不是从磁盘读取，而是实时生成后在 GPU 显存内保存，可以节省大量存储空间；理想状态下 cached shadow map 在第一帧生成好，后续不需要更新，这样就有近似于预计算的性能。

• cached shadow map 只对新添加的静态物体进行绘制 shadow depth，并持久化保存。
• temporary shadow map 先将 cached shadow map 的内容 copy 过来，再对动态物体进行绘制 shadow depth。

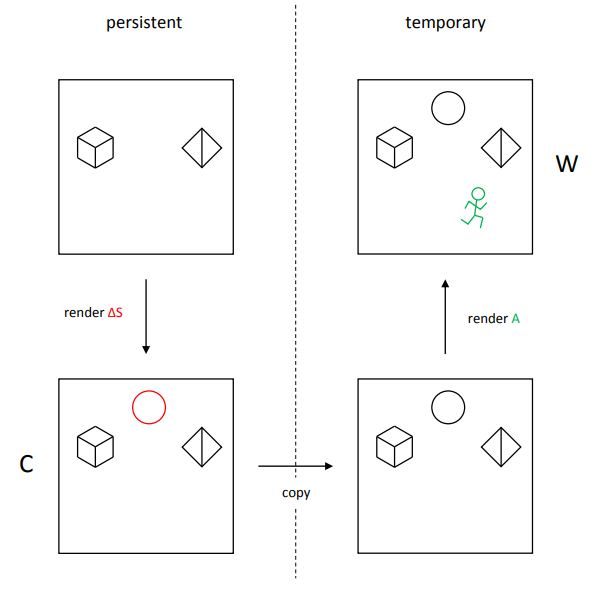
然而当光源发生平移时，cached shadow map 会需要对所有静态物体重新绘制 。

为了避免这种性能浪费，可以采用滚动优化：即只对 cached shadow map 中移动后产生的新区域进行更新，更具体地就是在 CPU 测试一遍有哪些静态物体在新区域上，若在则提交绘制。

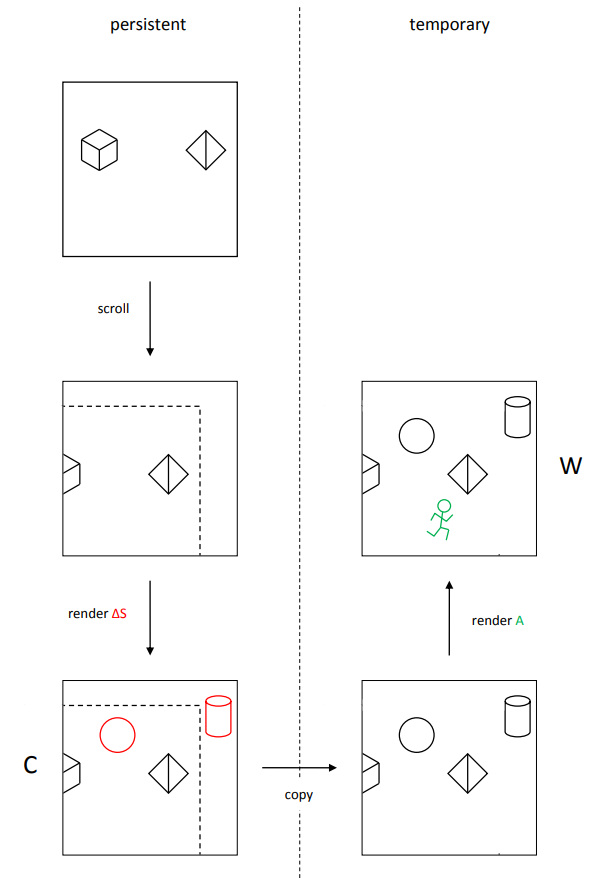
但需要说明的是，采用了滚动优化后，texel 的逻辑位置 \(P_{logic}\) 和物理存储位置 \(P_{physics}\) 往往不是一样的，因为在具体实现上需要记录 \(offset\)，当光源移动时就给 \(offset\) 添加相应的位移，最后通过 shift 操作将逻辑位置转换为物理存储位置：

\[P_{physics} = (P_{logic} + offset) \mod (resolution_{shadowmap}) \]

shadow map caching 方法天生适合于 point light/spot light 光源，在 Unreal Engine 中默认是启用该技术；但是对于方向光来说，可能还需要相当多的工程性改造，例如：CSM 总是根据视锥范围来构造的，如果应用于此是需要修改 CSM 的构造规则。

遮挡剔除

大家常说的遮挡剔除往往是用于玩家摄像机的，这可以帮我们剔除一些被遮挡的 receivers。但实际上遮挡剔除也可以用于光源摄像机：尽可能剔除被遮挡的 casters，来减少 draw call 数量。

常见的遮挡剔除方法如下，但不具体展开。

• CPU 软件光栅化：在 CPU 上利用软件光栅化将一些较大的 occluders（往往是美术预设的）绘制出来并得到一个低分辨率 z-buffer，然后再绘制其它小物体的包围盒来查询是否被遮挡。
• GPU Driven：在 compute shader 里利用 hi-z 和物体包围盒进行剔除，并利用 indirect draw 来绘制通过剔除测试的物体。
• 基于硬件 Occlusion Query：向 GPU 插入查询，查询模型包围盒是否被 z-buffer 遮挡，并将结果回读到 CPU 里。

视锥剔除

对于光源摄像机来说，视锥剔除往往起不到巨大的作用，因为在逻辑上光源的 view 往往是覆盖整个场景的。

因此我们得从玩家摄像机视角来做视锥剔除，但注意：不能直接根据 caster 是否与玩家视锥体相交来进行剔除，因为视锥外的 casters 仍可能产生阴影投射在 view frustum 内；因此需要考虑 caster 及 caster 自身产生的 shadow volume（阴影体积）组成的一个几何体。

当然在 CPU 里计算 caster 及其 shadow volume 是否与 view frustum 相交可能是比较费事的计算，这里有一些优化思路：

• 简化 caster 模型：使用 bounding box。
• 思维逆转！反向延长视锥体，而不是延长 caster。

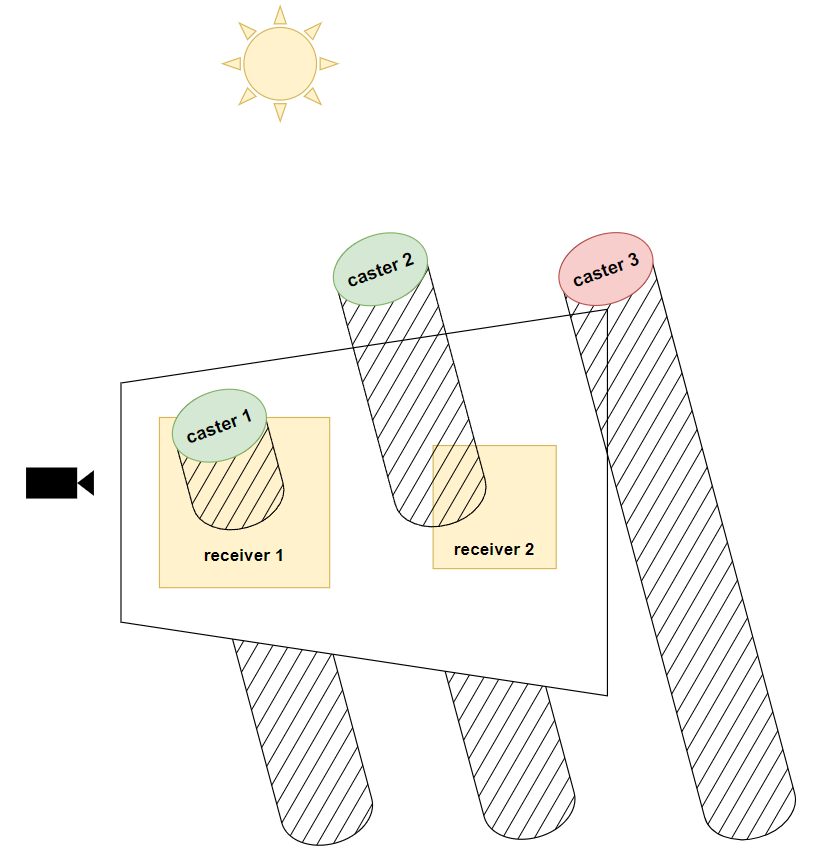
Receiver Mask [2011]

前面讲到的视锥剔除能在一定程度剔除 casters，但如果我们更进一步分析，实际上有效 casters 并不是与 view frustum 相交的 casters（及其 shadow volume），而是那些与至少一个 receiver 相交的 casters。

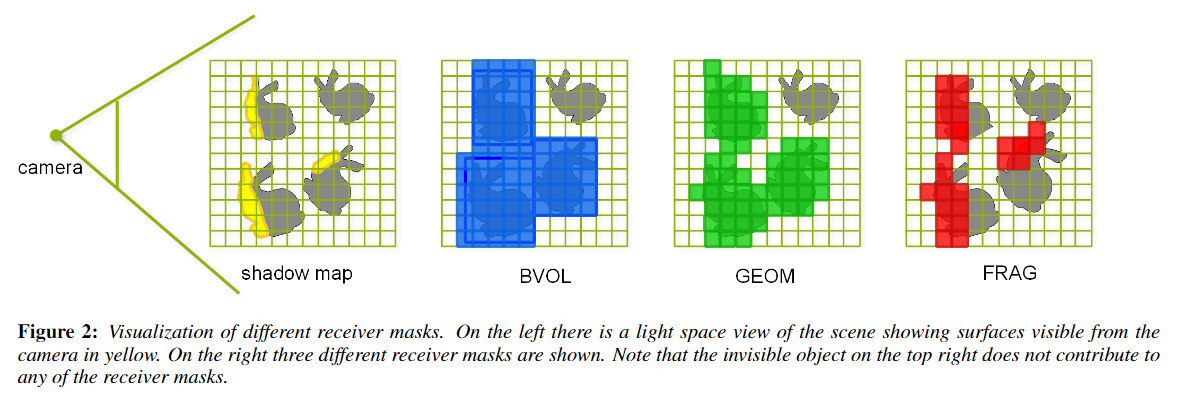
《Shadow caster culling for efficient shadow mapping》提供了一个这样的思路，在 light space 下先创建一张 mask texture，并绘制所有可见的 receivers 来写入 mask 值，然后就根据 caster 在 light space 下的范围是否存在 receivers mask 来决定是否对该 caster 进行 draw call。

具体的步骤可以拆解为三步：

1. 确定有哪些 receivers 可见：这里会在 CPU 里先对 receivers 进行常见的视锥剔除和遮挡剔除（渲染管线的老技巧了）。

2. 在 GPU 里为可见 receivers 绘制一张 light space mask texture，大致有以下生成的方式：

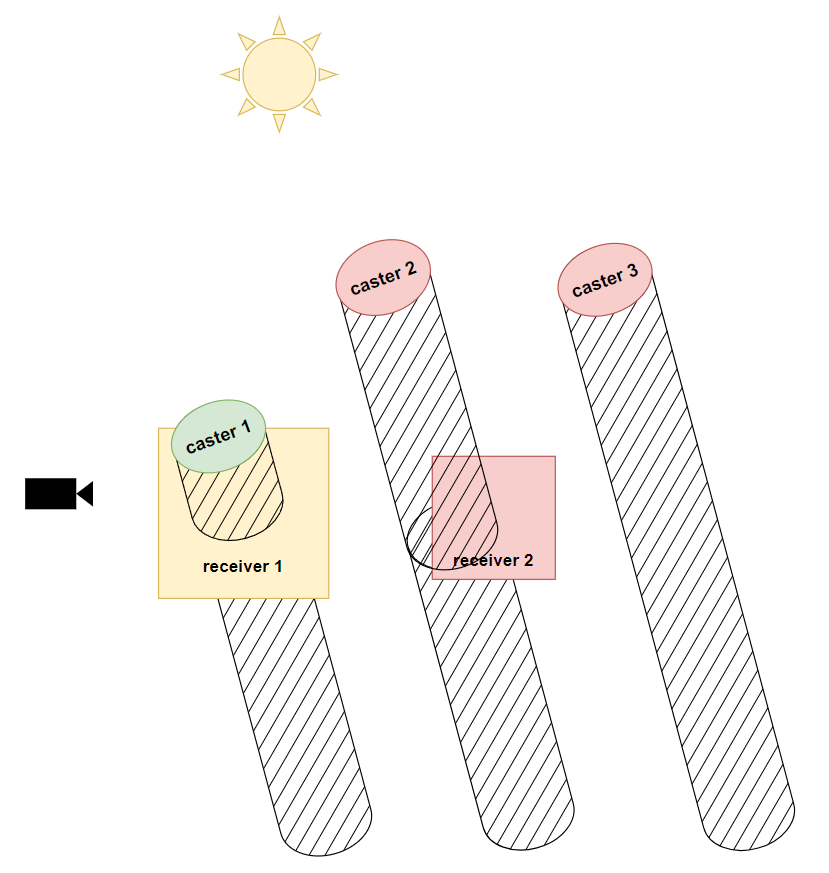
   • Bounding Volume Mask：最直接的方法。对可见 receivers 建立 bounding box，然后绘制这些 bounding boxes 并写入 mask。

   • Geometry Mask：直接绘制可见 receivers 写入 mask 和 shadow depth。

     很多时候，receiver 自身也是 caster，因此使用 geometry mask 后可以在后续第三步（渲染 shadow map 时）跳过这些 casters 的绘制。所以这类 mask 生成方式很多时候是 free lunch。

   • Bounding Volume Mask + Geometry Mask：结合两者的优点。

     • 上一帧最终在 light space 可见的 receivers 大概率本帧也会出现在 light space mask texture，因此只绘制这些 receivers（同时也得满足 camera 可见） 写入 mask 和 shadow depth。

     此时的 shadow map 只有上一帧 light space 的可见 receivers 写入的深度。

     另外，在后续第三步（渲染 shadow map 时）可以跳过这些绘制了 shadow depth 的 casters 的绘制。

     • 然后对所有 receivers 建立 bounding box，利用硬件 occlusion query 技术查询所有 boxes 是否被生成的 shadow map 所遮挡，如果没有则判断为在 light space 上本帧可见。

     该方法其实说白了就是在 light space 下又对 receivers 做了一次遮挡剔除，从而只需要精确绘制最靠近光源的那些 receivers。

   • Fragment Mask：直接绘制可见 receivers 写入 mask 和 shadow depth，但是在 fragment shader 中额外进行了变换到 camera space 并与 depth buffer 进行大小判断，如果 fragement 深度要更远，那么 discard 掉。

     该方法生成的每个 fragment shader 都需要读一次 camera space depth buffer，并做了一定的变换计算，这些都是潜在的额外开销，需要根据场景来测试使用 Bounding Volume + Geometry Mask 还是 Fragment Mask 方法。

     另外一提该方法有点类似于 camera space 下查 shadow map 来决定 fragments 是否在阴影区域，只不过角色互换了。实际上阴影问题本质上就是找 camera 和 light 同时能看见的 fragments。

   

3. 在绘制 shadow map 时，就可以在 CPU 利用硬件 occlusion query 技术来查询 casters 是否通过了 mask texture 的 stencil test，并由此决定是否绘制 casters。

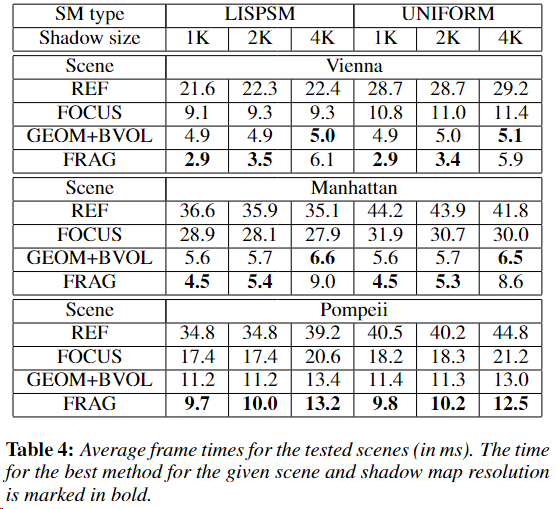
性能表现较好的 mask 方法基本就是 fragment mask 和 BVM+GM 这两种，下面是一些原 paper 性能数据：

参考

• [1] GAMES202-高质量实时渲染-闫令琪
• [2] Tutorial 16 : Shadow mapping | opengl-tutorial
• [3] Chapter 8. Summed-Area Variance Shadow Maps | NVIDIA Developer
• [4] Exponential Shadow Maps
• [5] 切换到ESM - KlayGE游戏引擎
• [6] Rendering Antialiased Shadows using Warped Variance Shadow Maps
• [7] Cascaded Shadow Maps | Rouslan Dimitrov NVIDIA Corporation
• [8] Cascade Shadow进阶之路
• [9] Virtual Shadow Maps in Unreal Engine | Unreal Engine 5.0 Documentation
• [10] Sparse Virtual Shadow Maps
• [11] 剔除：从软件到硬件 - 知乎 (zhihu.com)
• [12] 游戏中的动态阴影 - 知乎 (zhihu.com)
• [13] shadowmap压缩 - 知乎 (zhihu.com)
• [14] 2012 | CSM-Scrolling
• [15] Symposium on Interactive 3D Graphics and Games 2011 | Shadow caster culling for efficient shadow mapping