基于物理的渲染（1）光谱与辐射度量学

目录

• 光谱表示
  • 系数 SPD
  • XYZ 颜色空间
  • RGB 颜色空间
  • 非线性颜色空间
    • sRGB 颜色
    • HSV 颜色
• 辐射度量学（Radiometry）
  • 立体角（Solid Angle）
  • Radiant Energy & Radiant Flux（Power）
  • Radiant Intensity
  • Irradiance
  • Radiance
• 渲染方程（The Rendering Equation）
• 参考

所谓的 基于物理的渲染（Physically Based Rendering，PBR），实际上就是整套渲染流程的每个成分，包含 light transport（光路）、material（材质）、lighting（光照）、camera（摄像机）等，这些都是在遵循真实世界物理理论的基础上所建立的模型。

目前绝大部分基于物理的渲染理论基础都是基于几何光学，而实际上它还不完全是真实世界的物理，因为它只体现了光的几何直线传播，没有体现光的波动性，这也是最近新渲染理论关注的点：波动光学。

光谱表示

现实世界的颜色实际上都是不同波长的电磁波叠加而成。波长是电磁波的属性，人眼可以感受到的电磁波范围约为 400nm-700nm。光谱可以对光在此一定范围内的能量进行度量，通常采用 SPD（Spectral Power Distribution, 光谱功率分布）来描述光源的颜色和强度以及物体表面在不同波长下的反射和折射特性。

SPD 是一个连续函数，表示在不同波长下的光源强度；通过对 SPD 进行采样，可以获得在特定波长下的光源强度。

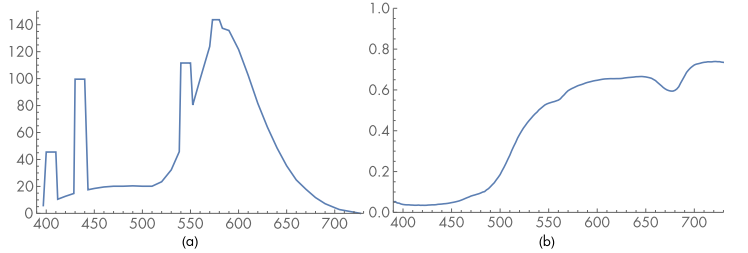
(a) 荧光灯的频谱分布和 (b) 柠檬皮的反射率。波长 400nm 左右是偏蓝光，而波长中段是绿色和黄色，波长 700nm 左右是红光。

系数 SPD

计算机中只能以离散的形式存储数据，为了模拟 SPD，可以存储若干个 SPD 系数：即每隔一定长度的波长就放置一个采样点（对应下图黑色点），采样点记录对应波长的光源强度（即所谓 SPD 系数）；要采样某个特定波长的光源强度，则需要找到该波长相邻的两个采样点的强度并进行线性插值来获得。

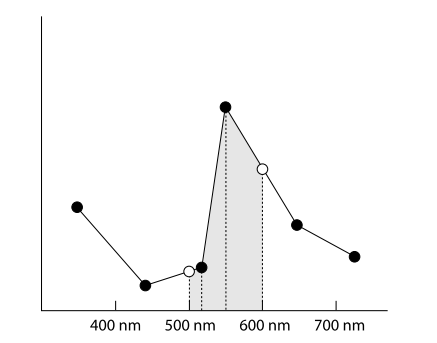
理论上只要采样点够多，系数 SPD 就足够接近原始 SPD 函数，也就更准确表达 SPD。

XYZ 颜色空间

颜色感知的三刺激理论 （tristimulus theory）表明，人类视觉系统的一个非凡性质是可只用三个值 \(x_λ\) , \(y_λ\) 和 \(z_λ\) 就能为人类观察者准确表示所有可见的颜色。实际上就是让 SPD 以三种基函数 \(X(λ)\),\(Y(λ)\) 和 \(Z(λ)\) 的线性组合来表达，如图所示为三种基函数的形状：

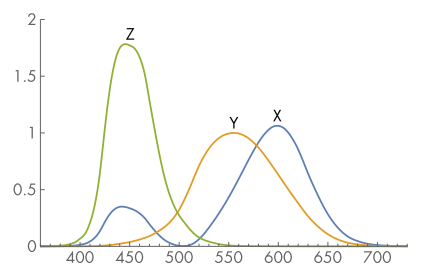
给定 SPD 即 \(S(λ)\)，通过积分 \(S(\lambda)\) 和对应基函数的乘积便可算得这些 \(x_λ\) , \(y_λ\) 和 \(z_λ\) ：

\[\begin{aligned} & x_\lambda=\int_\lambda X(\lambda) S(\lambda) \mathrm{d} \lambda \\ & y_\lambda=\int_\lambda Y(\lambda) S(\lambda) \mathrm{d} \lambda \\ & z_\lambda=\int_\lambda Z(\lambda) S(\lambda) \mathrm{d} \lambda \end{aligned} \]

当然，仅用这三种函数肯定不能精确表达所有 SPD，之所以 XYZ 颜色能表示所有可见颜色，是因为对于人类观察者来说，还存在一个现象：同色异谱，简单来说就是对于人类观察者来说具有相同的视觉呈现，但是却可以是完全不同的光谱。

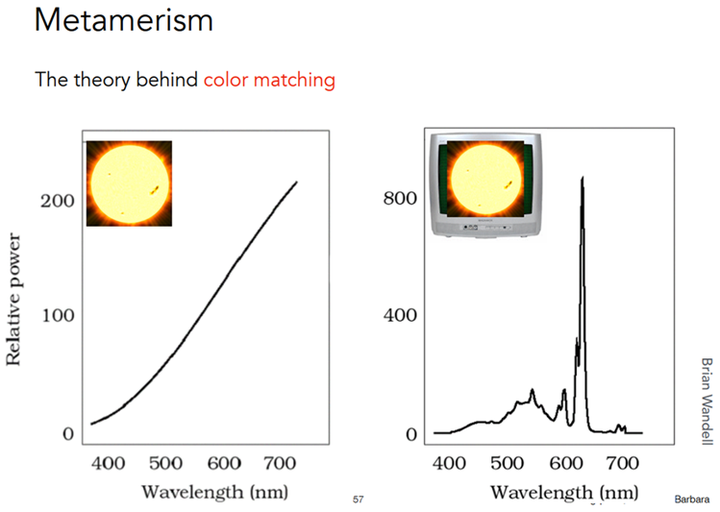
正因为同色异谱现象，国际照明委员会（CIE）才制定了 XYZ 颜色空间标准以方便表示人类所有可见颜色。尽管很方便表示颜色表现，但在光谱计算中，XYZ 不是特别好的基函数。

例如，在光源和反射率相乘的情况下，XYZ 颜色相乘的结果可能明显不同于 SPD 相乘后再计算出的 XYZ 颜色。

RGB 颜色空间

XYZ 利用三个浮点数去表示 SPD 是非常方便的。但由于显示器的物理性质不同，每个设备自己的基函数都会有所不同，因此才有了设备相关的 RGB 颜色空间。

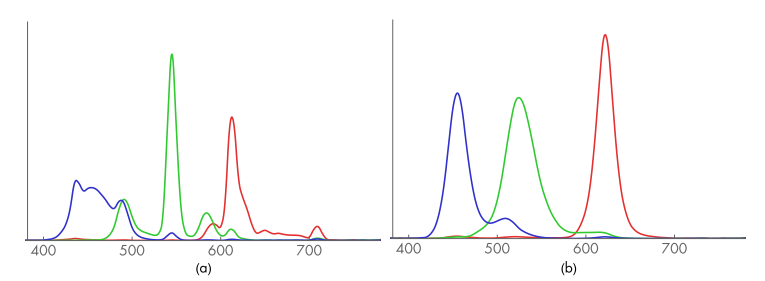
(a) 为 LCD 显示器的 RGB 基函数，(b) 为 LED 显示器的 RGB 基函数，两种显示器有完全不同的基函数形状。

下面是不同的 RGB 标准所占据的颜色空间范围（注：有颜色的区域为人眼可观察到的颜色）。

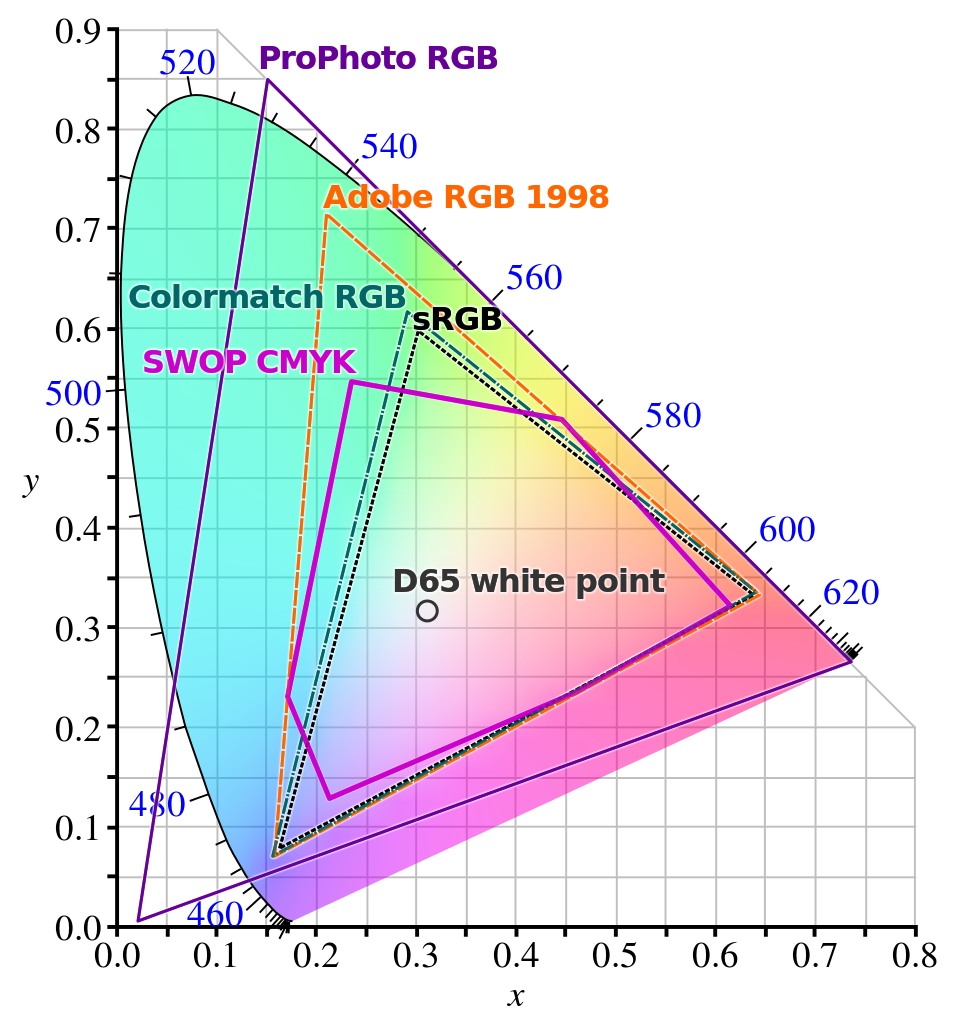
在现实中，人们制定了各种 RGB 标准之后，以后生产的设备会遵循某一 RGB 标准，从而统一了较多的设备差异。目前 sRGB 标准仍是显示器设备的主流标准，而 Adobe RGB 是第二常用的广域颜色标准（比 sRGB 能表示更大范围的颜色）。

与 XYZ 一样，RGB 也是由三个基向量 \(R(\lambda)\),\(G(\lambda)\),\(B(\lambda)\) 线性组合而成，其 r，g，b 值可通过以下积分式算得：

\[\begin{aligned} r=\int R(\lambda) S(\lambda) \mathrm{d} \lambda \\ g=\int G(\lambda) S(\lambda) \mathrm{d} \lambda \\ b=\int B(\lambda) S(\lambda) \mathrm{d} \lambda \end{aligned} \]

无论 RGB 采用什么颜色标准，只要其由三个基向量线性组合而成，就属于线性空间（XYZ 同理），因此 XYZ 颜色空间和各种 RGB 颜色空间均可以通过矩阵变换来互相转换。

如下为 XYZ 空间转换到指定 RGB 空间所需的矩阵（当然 RGB 空间转换回 XYZ 空间所需的矩阵只需要转换矩阵的逆即可）：

RGB 颜色空间	XYZ to RGB 转换矩阵
Adobe RGB	\(\left[\begin{array}{ccc}2.0413690 & -0.5649464 & -0.3446944 \\-0.9692660 & 1.8760108 & 0.0415560 \\0.0134474 & -0.1183897 & 1.0154096\end{array}\right]\)
sRGB	\(\left[\begin{array}{ccc}3.2404542 & -1.5371385 & -0.4985314 \\-0.9692660 & 1.8760108 & 0.0415560 \\0.0556434 & -0.2040259 & 1.0572252\end{array}\right]\)
Apple RGB	\(\left[\begin{array}{ccc}2.9515373 & -1.2894116 & -0.4738445 \\-1.0851093 & 1.9908566 & 0.0372026 \\0.0854934 & -0.2694964 & 1.0912975\end{array}\right]\)
CIE RGB	\(\left[\begin{array}{ccc}2.3706743 & -0.9000405 & -0.4706338 \\-0.5138850 & 1.4253036 & 0.0885814 \\0.0052982 & -0.0146949 & 1.0093968\end{array}\right]\)

在模拟光照传播时，就少不了颜色计算。而常用的实时渲染中，我们都会选取 RGB 来表示颜色，并在 RGB 线性空间下进行计算。部分 RGB 颜色标准中默认是在非线性空间（如 sRGB 颜色标准），我们往往需要将其逆伽马校正成线性空间的 sRGB 颜色才能进行正确的颜色计算（也包括上面提过的颜色空间变换）。

RGB 线性空间下的颜色计算在加法上是正确的，然而在乘法上却不准确（常见于乘 BRDF）。推导过程可看 PBRTv4，但其实直观上也很容易理解：准确的颜色乘法应当是每个波长上的反射率和对应波长上的辐射量进行乘法来得到一个新的 SPD，最后再将其转换为用于最终显示的 RGB 颜色。

如果我们全程使用 SPD 来进行颜色计算，那么这种便称为基于光谱的渲染技术，这种渲染往往计算量巨大（基本只能离线），但是能够进行精确的光学计算，一般用于专业级模拟光学的领域。

非线性颜色空间

sRGB 颜色

人类的视觉系统还有一个特征：对较暗区域的颜色变化更敏感。如下图，用 RGB 线性空间表示一个颜色，虽然数值上 [128, 128, 128] 是一半的颜色值，很明显在人类视觉上 [56, 56, 56] 才是一半的亮度。

因此为了优化颜色编码，让更多数值去表示较暗区域， sRGB 标准默认采用了非线性编码：将正常线性空间的 RGB 颜色值各通道进行了 $\frac{1}{2.2}\approx 0.45 $ 幂次方，从而更加突出暗部细节。

\[sRGB = RGB^{\frac{1}{2.2}} \]

但是要注意，我们在进行颜色计算时，仍然需要在线性空间下计算才能保持准确性（尽管还是没 SPD 准确），也就意味着：

• 当去读取普通 RGB 纹理（实际上说的就是线性空间），可以直接读取并进行相关颜色计算。
• 当去读取 sRGB 纹理（实际上就是说非线性空间）时，而我们往往需要将 sRGB 颜色逆伽马校正（进行 \(2.2\) 幂次方）回线性空间的 RGB 颜色后才能进行相关颜色计算。

sRGB 纹理可以更好地保留暗部细节，常用于存储人眼可直接观察的纹理：如 albedo texture、lightmap 等。而对于与人眼直接观察无关的纹理，便一般使用普通 RGB 纹理：如 normal texture。

本处不会提及显示屏伽马相关，因为现代显示屏很多都已经不是阴极射线管（CRT显示器），很多时候游戏都会让玩家自己手动调节伽马值，因此这里只讲 sRGB 编码。

HSV 颜色

HSV 是另一种表示颜色的方式，和 RGB 一样由三个分量表达，分别为：

• Hue（色相）
• Saturation（饱和度）
• Value（明度）

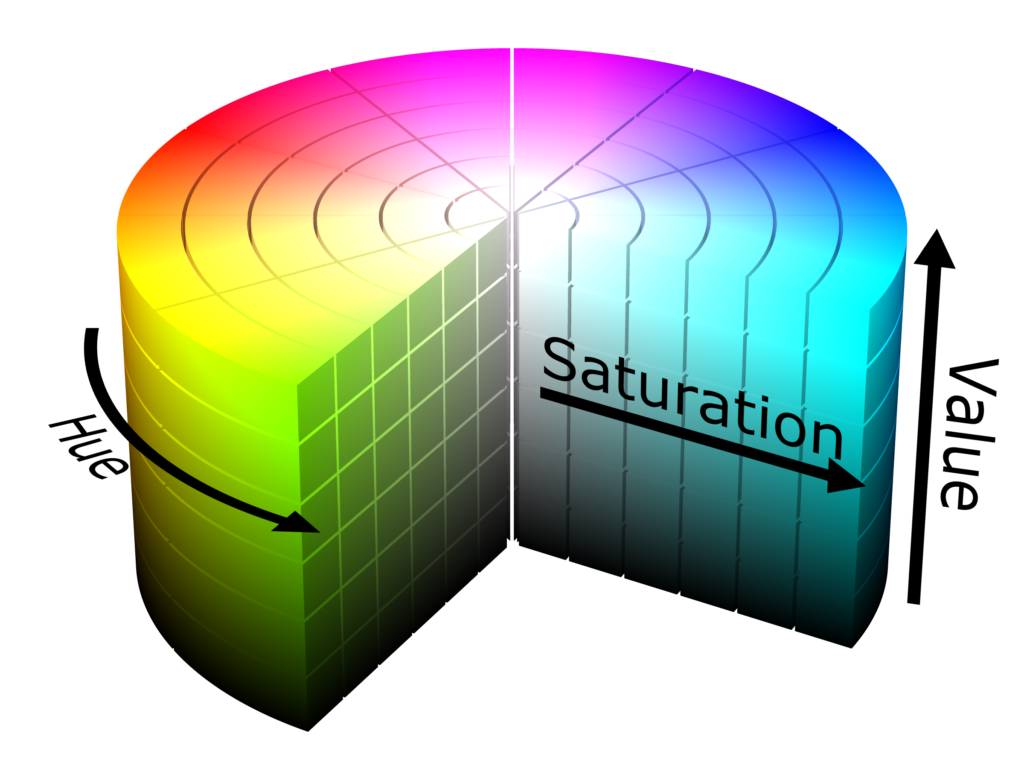
HSV 有着比 RGB 更直观的参数，更方便面向用户，并且还常用于图像处理（因为这三个分量很好的提取了颜色的三类特征）。更多的就不具体展开了。

辐射度量学（Radiometry）

现在我们需要从能量的角度上去理解光的传播、光在空间中的分布，为此需要一些物理计量单位，而这些也就刚好是辐射度量学的范畴。

立体角（Solid Angle）

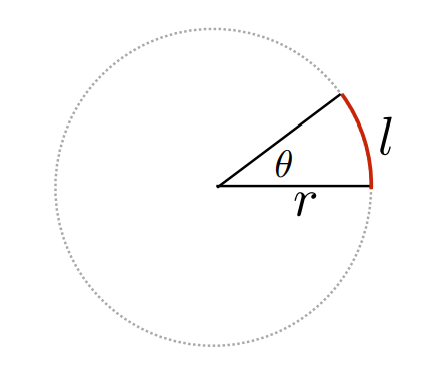
角度（Angle）：从二维上看，用圆上所对应的弧长与半径之比来定义一个角度，而且这个角度是与圆半径大小无关的（因为使用了弧长和半径之比）。

• \(\theta = \frac{l}{r}\)
• 任何圆都有 \(2\pi\) 弧度

立体角（Solid Angle）: 推广至三维，类似地，用球面上的面积A与所对应的半径平方之比来定义一个立体角，而且这个立体角同样是与球体半径大小无关的（因为使用了球面上的面积A与所对应的半径平方之比）。

• \(\omega = \frac{A}{r^2}\)
• 任何球体都有 \(4\pi\) steradians

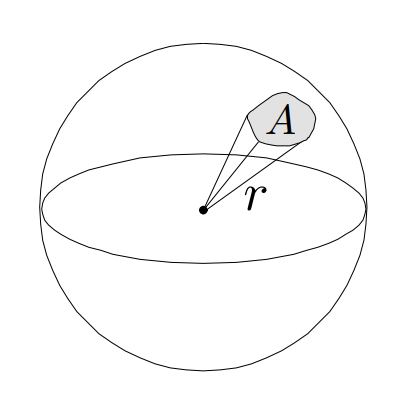
考虑下图所示空间中的点光源，以球心为顶点的无限长锥体内，任何截面（与任意半径的球体相截）接收到的光子能量应该是一样的。换句话说，近处较小面积的表面和远处较大面积的表面所接收到的 Power 应该相同。立体角（Solid Angle）正可以表示这样一个比例关系（球面面积A与半径平方之比）。

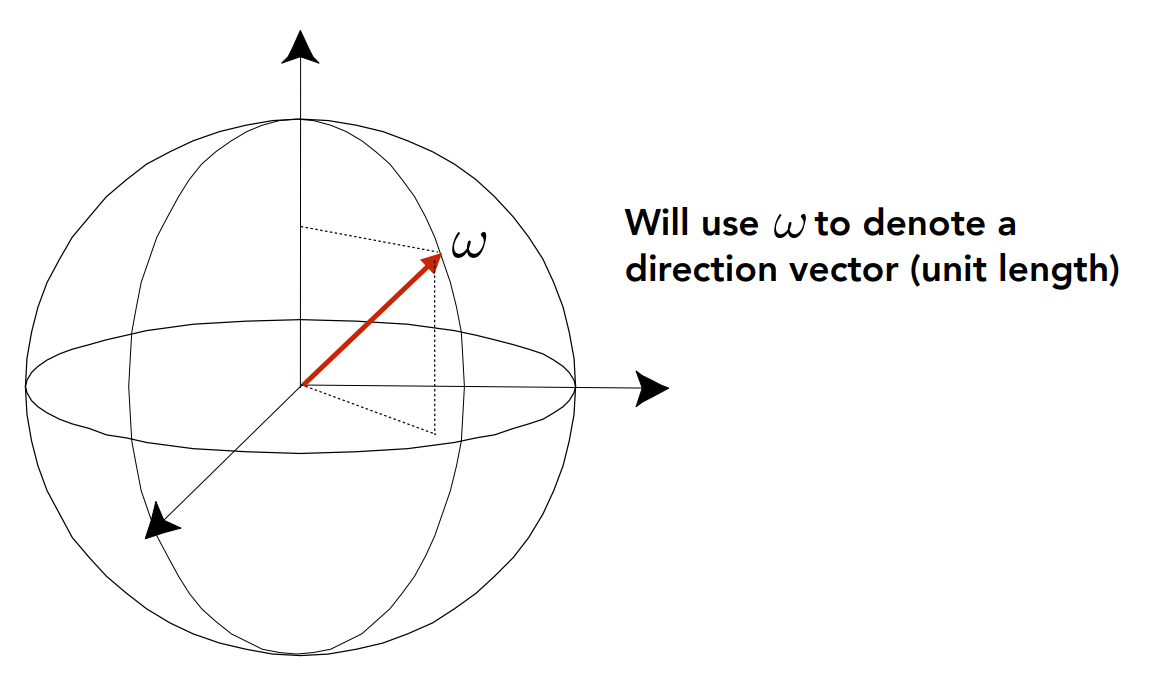
另外，角度 \(\theta\) 可以代表一个 2D 有向单位向量（2D 方向），而立体角 \(\omega\) 也可以被用来代表一个 3D 有向单位向量（3D 方向）。

Radiant Energy & Radiant Flux（Power）

Radiant Energy：能量

\[Q \]

单位 \([J=Joule]\)

Radiant Flux / Power：单位时间的能量（功率）

\[\Phi=\frac{dQ}{dt} \]

单位 \(\\ [W=Watt], [lm=lumen]^*\)

物体表面总是时时刻刻接受光子能量，又时时刻刻散发光子能量，因此图形学中常将 Radiant Flux / Power用来衡量光照强度，而几乎不用 Radiant Energy。

Radiant Intensity

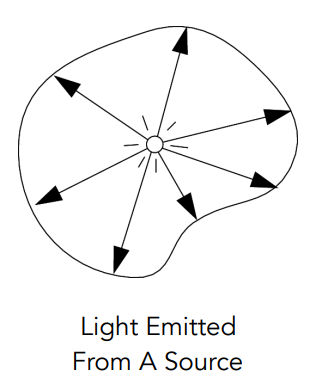
Radiant Intensity：每单位立体角的 Power，常用于衡量光源朝某个立体角方向辐射出去的 Power。

\[I(\omega) \equiv \frac{\mathrm{d} \Phi}{\mathrm{d} \omega} \]

单位 \(\left[\frac{\mathrm{W}}{\mathrm{sr}}\right], \left[\frac{\mathrm{lm}}{\mathrm{sr}}=\mathrm{cd}=\mathrm{candela}\right]\)

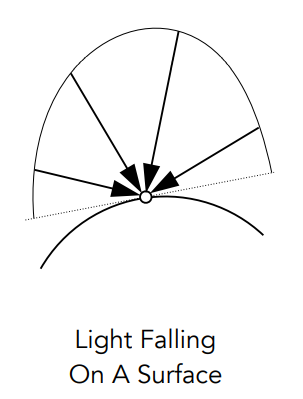
Irradiance

Irradiance：每单位面积的 Power，常用于衡量表面上每单位面积接受各个立体角方向入射的 Power 总和

\[E(\mathbf{x}) \equiv \frac{\mathrm{d} \Phi(\mathbf{x})}{\mathrm{d} A} \]

单位 \(\left[\frac{\mathrm{W}}{\mathrm{m}^{2}}\right],\left[\frac{\mathrm{lm}}{\mathrm{m}^{2}}=\operatorname{lux}\right]\)

Radiance

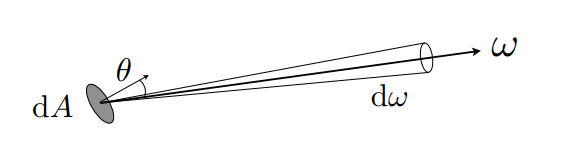
Radiance：每单位立体角，每单位投影面积的 Power，常用于衡量表面上每单位面积朝某个立体角方向反射的 Power。

\[L(\mathrm{x}, \omega) \equiv \frac{\mathrm{d}^{2} \Phi(\mathrm{x}, \omega)}{\mathrm{d} \omega \mathrm{d} A \cos \theta} \]

单位 \(\left[\frac{\mathrm{W}}{\mathrm{sr} \mathrm{m}^{2}}\right],\left[\frac{\mathrm{cd}}{\mathrm{m}^{2}}=\frac{\operatorname{lm}}{\mathrm{sr} \mathrm{m}^{2}}=\mathrm{nit}\right]\)

渲染方程（The Rendering Equation）

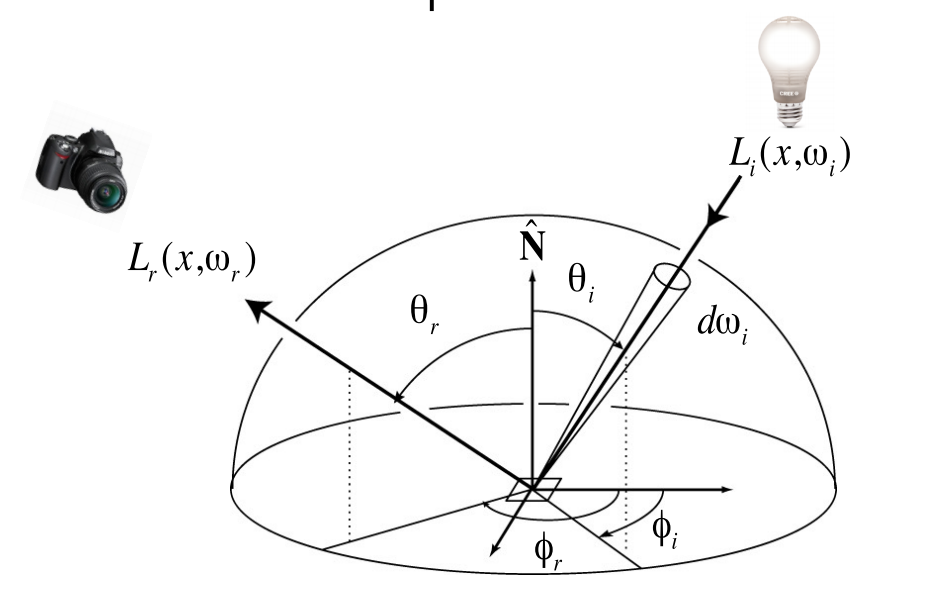
有了上述的概念，那么我们就可以用公式这样描述对某个完全不透明 shading point 的渲染：一个点 \(x\)​ 接受各个方向（\(\omega_i\in \Omega^+\)​）的入射光 \(L_i\)​ 后，则往某个指定方向 \(\omega_r\)​ 反射的光为 \(L_r\)​，并有：

\[L_{r}\left(x, \omega_{r}\right)=\int_{\Omega^{+}} L_{i}\left(x, \omega_{i}\right) f_{r}\left(x, \omega_{i}, \omega_{r}\right)\left(n \cdot \omega_{i}\right) \mathrm{d} \omega_{i} \]

倘若点 \(x\) 还包含有自发光（Emissive） \(L_e\)，那么完整的渲染方程应该如下：

\[L_{r}\left(x, \omega_{r}\right)=L_{e}\left(x, \omega_{r}\right)+\int_{\Omega^{+}} L_{i}\left(x, \omega_{i}\right) f_{r}\left(x, \omega_{i}, \omega_{r} \right)\left(n \cdot \omega_{i}\right) \mathrm{d} \omega_{i} \]

• \(f_{r}\left(x, \omega_{i}, \omega_{r}\right)\)​​ 表示为某个光入射点表面后孤立的反射情况，也就是马上要讲的 BRDF，因为光传播到不同物体表面上的反射情况是各不相同的，例如对于glossy的物体（光滑的镜子）和diffuse的物体（粗糙的木头），前者往往更容易形成镜面反射的光，而后者则是更容易形成漫反射的光。

这里的渲染方程主要是面向不透明物体，一般用 BRDF 足以表示该反射情况；对于别的特殊材质，例如半透明/透明物体，一般会使用 BSDF；对于次表面散射物体，就会用 BSSRDF ... 这些双向分布函数可以统一称为 BxDF。

• 积分域 \(\Omega^+\) 的意思是上半球的范围，这是因为 shading point 不可能被从背面的下半球面传来的光线打到。

实际上，如果物体是半透明的，还是可能被背面下半球面传来的光线打到，在包含 BSDF 的渲染方程中会包含整个球 \(\Omega\) 范围。

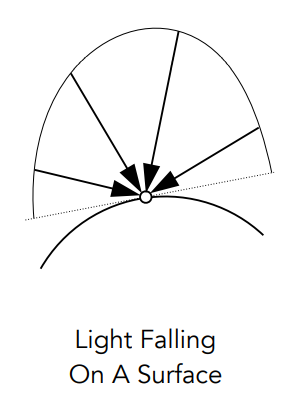
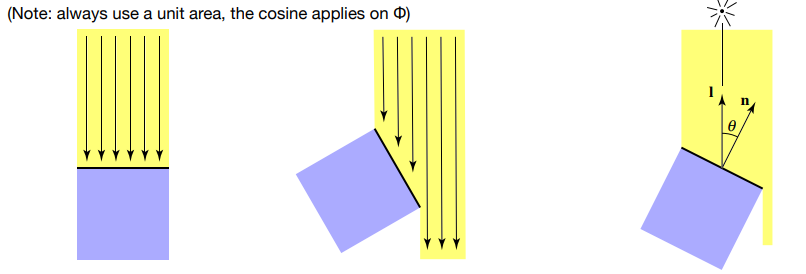
• \((n\cdot\omega_i)\) 这个点积则意味着入射方向与表面法线夹角越小，那么这个表面能够接受的 Power 就越多：

参考

• [1] GAMES101-现代计算机图形学入门-闫令琪
• [2] GAMES202-高质量实时渲染-闫令琪
• [3] 知乎 |【基于物理的渲染（PBR）白皮书】（一） 开篇：PBR核心知识体系总结与概览
• [4] Pharr M, Jakob W, Humphreys G. Physically based rendering: From theory to implementation[M]. Morgan Kaufmann, 2016.
• [5] 游戏色彩101（入门必看） - 知乎 (zhihu.com)
• [6] 色彩空间基础 - 知乎 (zhihu.com)