李沐动手学深度学习14——循环神经网络基础
循环神经网络
如果说卷积神经网络可以有效的处理空间信息,循环神经网络则可以更好地处理序列信息。
循环神经网络通过引入状态变量存储过去的信息和当前的输入,从而可以确定当前的输出。
自回归模型
1.若想预测xt对应的值,使用固定长度时间跨度的数据xt-1到xt-τ进行预测,这种模型叫自回归模型。
2.在自回归的基础上,设想观测数据x是有一个不可观测的隐变量z驱动,而z本身又遵循某种自回归,这种模型叫隐变量自回归模型。
以下代码使用sin函数与随机噪音生成模拟数据,以τ值为4的两层多层感知机训练简单的自回归模型:
实验发现:
1.在训练集中,模型表现合格(时间<600)
2.在时间大于600后,模型图像趋于一条直线(常数),无法拟合数据。此时算法效果差,原因是错误的累积效应
3.为验证错误的累积效应,将k值设为1,4,16,64,分别计算若模型模拟k步后的效果,发现k大于4后,模型预测效果差
import torch from torch import nn from d2l import torch as d2l import matplotlib.pyplot as plt def init_weight(m): if type(m) == nn.Linear: nn.init.xavier_uniform_(m.weight) def get_net(): net = nn.Sequential(nn.Linear(4, 10), nn.ReLU(), nn.Linear(10, 1)) net.apply(init_weight) return net def train(net, train_iter, loss, epochs, lr): trainer = torch.optim.Adam(net.parameters(), lr) for epoch in range(epochs): for X, y in train_iter: trainer.zero_grad() l = loss(net(x), y) l.sum().backward() trainer.step() print(f'epoch {epoch + 1}, 'f'loss: {d2l.evaluate_loss(net, train_iter, loss):f}') if __name__ == "__main__": T = 1000 time = torch.arange(1, T + 1, dtype=torch.float32) x = torch.sin(0.01 * time) + torch.normal(0, 0.2, (T,)) d2l.plot(time, [x], 'time', 'x', xlim=[1, 1000], figsize=(6, 3)) # plt.show() # 将τ值设为4,即自回归模型以前4个点作为输入 tau = 4 features = torch.zeros((T - tau, tau)) for i in range(tau): features[:, i] = x[i: T - tau + i] labels = x[tau:].reshape((-1, 1)) # 使用前600个数据作为训练集 batch_size, n_train = 16, 600 train_iter = d2l.load_array((features[:n_train], labels[:n_train]), batch_size, is_train=True) loss = nn.MSELoss(reduction='none') net = get_net() train(net, train_iter, loss, 5, 0.01)
使用以下代码作文本预处理:
import collections import re from d2l import torch as d2l def read_time_machine(): with open(d2l.download('time_machine'), 'r') as f: lines = f.readlines() return [re.sub('[^A-Za-z]+', ' ', line).strip().lower() for line in lines] def tokenize(lines, token='word'): if token == 'word': return [line.split() for line in lines] elif token == 'char': return [list(line) for line in lines] else: print('error: unknown type of token') class Vocab: def __init__(self, tokens=None, min_freq=0, reserved_tokens=None): if tokens is None: tokens = [] if reserved_tokens is None: reserved_tokens = [] counter = count_corpus(tokens) self._token_freqs = sorted(counter.items(), key=lambda x:x[1], reverse=True) self.idx_to_token = ['<unk>'] + reserved_tokens self.token_to_idx = {token: idx for idx, token in enumerate(self.idx_to_token)} for token, freq in self._token_freqs: if freq < min_freq: break if token not in self.token_to_idx: self.idx_to_token.append(token) self.token_to_idx[token] = len(self.idx_to_token) - 1 def __len__(self): return len(self.idx_to_token) def __getitem__(self, tokens): if not isinstance(tokens, (list, tuple)): return self.token_to_idx.get(tokens, self.unk) return [self.__getitem__(token) for token in tokens] def to_tokens(self, indices): if not isinstance(indices, (list, tuple)): return self.idx_to_token[indices] return [self.idx_to_token[index] for index in indices] @property def unk(self): return 0 @property def token_freq(self): return self._token_freqs def count_corpus(tokens): if len(tokens) == 0 or isinstance(tokens[0], list): tokens = [token for line in tokens for token in line] return collections.Counter(tokens) def load_corpus_time_machine(max_tokens=-1): lines = read_time_machine() tokens = tokenize(lines, 'char') vocab = Vocab(tokens) # 因为时光机器数据集中的每个文本行不一定是一个句子或一个段落, # 所以将所有文本行展平到一个列表中 corpus = [vocab[token] for line in tokens for token in line] if max_tokens > 0: corpus = corpus[:max_tokens] return corpus, vocab if __name__ == "__main__": d2l.DATA_HUB['time_machine'] = (d2l.DATA_URL + 'timemachine.txt', '090b5e7e70c295757f55df93cb0a180b9691891a') lines = read_time_machine() # print(f'# 文本总行数: {len(lines)}') # print(lines[0]) # print(lines[10]) tokens = tokenize(lines) #for i in range(11): # print(tokens[i]) vocab = Vocab(tokens) print(list(vocab.token_to_idx.items())[:10]) for i in [0, 10]: print('文本: ', tokens[i]) print('索引: ', vocab[tokens[i]])
语言模型:
假设长度为T 的文本序列中的词元依次为x1, x2, . . . , xT 。于是,xt(1 ≤ t ≤ T )可以被认为是文本序列在时间步t处的观测或标签。
在给定这样的文本序列时,语言模型(language model)的目标是估计序列的联合概率:
P (x1, x2, . . . , xT ).
从基本概率规则开始:
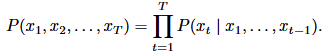
例如:
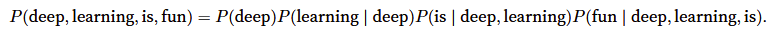
有时要计算给定前几个单词后出现某个单词的条件概率,这些概率就是语言模型的参数。一种稍微不太准确的方法是:
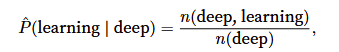
上公式中分子为deep learning单词出现的次数,分母为deep单词出现的次数。不过有时一些不常见的单词组合可能只会在数据集中出现二三次,或者数据集过小,
一种解决方案是执行某种形式的拉普拉斯平滑,在所有计数中添加一个小常量:
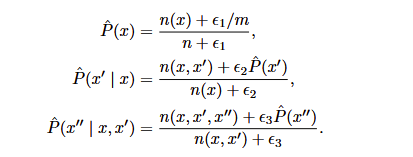
其中,ϵ1, ϵ2和ϵ3是超参数。
但是还会遇到其他问题,比如上述方法完全忽略了单词的含义,比如不能处理同义词等情况。因此一个模型如果只是简单地统计先前“看到”的单词序列频率,那么模型面对这种问题肯定是表现不佳的。
回想之前对马尔可夫模型的讨论,如果P (xt+1 | xt, . . . , x1) = P (xt+1 | xt),则序列上的分布满足一阶马尔可夫性质。这种性质推导出了许多可以应用于序列建模的近似公式:
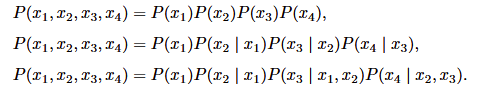
通常,涉及一个、两个和三个变量的概率公式分别被称为 一元语法(unigram)、二元语法(bigram)和三元语法(trigram)模型
自然语言统计:
查看10个最常用的单词:
d2l.DATA_HUB['time_machine'] = (d2l.DATA_URL + 'timemachine.txt', '090b5e7e70c295757f55df93cb0a180b9691891a') tokens = p2.tokenize(p2.read_time_machine()) corpus = [token for line in tokens for token in line] vocab = d2l.Vocab(corpus) print(vocab.token_freqs[:10])

查看所有单词的词频
freqs = [freq for token, freq in vocab.token_freqs] d2l.plot(freqs, xlabel='token: x', ylabel='frequency: n(x)', xscale='log', yscale='log') plt.show()
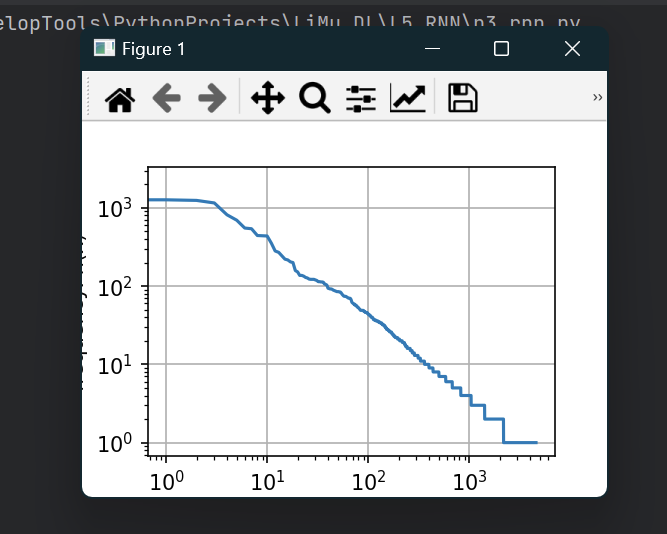
除了前几个单词,单词的词频大概呈指数关系。
再查看二元语法、三元语法的频率分布:
bigram_vocab = d2l.Vocab(bigram_tokens)
trigram_tokens = [' '.join(triple) for triple in zip(
corpus[:-2], corpus[1:-1], corpus[2:])]
trigram_vocab = d2l.Vocab(trigram_tokens)
bigram_freqs = [freq for token, freq in bigram_vocab.token_freqs]
trigram_freqs = [freq for token, freq in trigram_vocab.token_freqs]
d2l.plot([freqs, bigram_freqs, trigram_freqs], xlabel='token: x',
ylabel='frequency: n(x)', xscale='log', yscale='log',
legend=['unigram', 'bigram', 'trigram'])
plt.show()
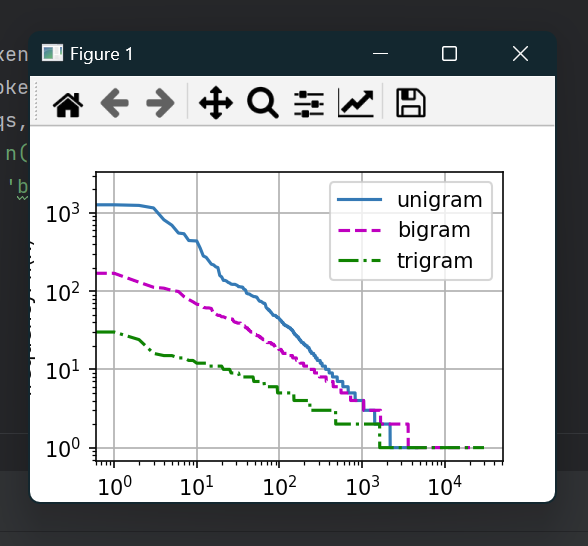
发现:
除了一元语法词,n元语法词的频率也呈指数分布。
n元组的数量没有变多,说明语言不是随机的组合,而是更具结构化。
因为之前提到的问题,拉普拉斯平滑不适合语言建模。因此使用基于深度学习的模型
循环神经网络:
带隐状态的循环神经网络:
某时刻的隐状态的计算,是根据1.前一时刻的隐状态,2.当前状态,3.偏置,计算出来的。隐状态的维度取决于num_hiddens参数设置
困惑度:
对困惑度的理解是,下一个词元的实际选择数的调和平均数,即平均面临n个等概率选择。使用困惑度度量模型的质量。
动手实现循环神经网络的代码:
import math import torch from torch import nn from torch.nn import functional as F import matplotlib.pyplot as plt from d2l import torch as d2l import p3_lnn_dataSet as p3 def get_params(vocab_size, num_hiddens, device): num_inputs = num_outputs = vocab_size def normal(shape): return torch.randn(size=shape, device=device) * 0.01 # 隐藏层参数 W_xh = normal((num_inputs, num_hiddens)) W_hh = normal((num_hiddens, num_hiddens)) b_h = torch.zeros(num_hiddens, device=device) # 输出层参数 W_hq = normal((num_hiddens, num_outputs)) b_q = torch.zeros(num_outputs, device=device) # 附加梯度 params = [W_xh, W_hh, b_h, W_hq, b_q] for param in params: param.requires_grad_(True) return params def init_rnn_state(batch_size, num_hiddens, device): return (torch.zeros((batch_size, num_hiddens), device=device), ) def rnn(inputs, state, params): # inputs的形状:(时间步数量,批量大小,词表大小) W_xh, W_hh, b_h, W_hq, b_q = params H, = state outputs = [] # X的形状:(批量大小,词表大小) for X in inputs: H = torch.tanh(torch.mm(X, W_xh) + torch.mm(H, W_hh) + b_h) Y = torch.mm(H, W_hq) + b_q outputs.append(Y) return torch.cat(outputs, dim=0), (H,) class RNNModelScratch: """从零开始实现的循环神经网络模型""" def __init__(self, vocab_size, num_hiddens, device, get_params, init_state, forward_fn): self.vocab_size, self.num_hiddens = vocab_size, num_hiddens self.params = get_params(vocab_size, num_hiddens, device) self.init_state, self.forward_fn = init_state, forward_fn def __call__(self, X, state): X = F.one_hot(X.T, self.vocab_size).type(torch.float32) return self.forward_fn(X, state, self.params) def begin_state(self, batch_size, device): return self.init_state(batch_size, self.num_hiddens, device) def predict_ch8(prefix, num_preds, net, vocab, device): """在prefix后面生成新字符""" state = net.begin_state(batch_size=1, device=device) outputs = [vocab[prefix[0]]] get_input = lambda: torch.tensor([outputs[-1]], device=device).reshape((1, 1)) for y in prefix[1:]: # 预热期 _, state = net(get_input(), state) outputs.append(vocab[y]) for _ in range(num_preds): # 预测num_preds步 y, state = net(get_input(), state) outputs.append(int(y.argmax(dim=1).reshape(1))) return ''.join([vocab.idx_to_token[i] for i in outputs]) def grad_clipping(net, theta): #@save """裁剪梯度""" if isinstance(net, nn.Module): params = [p for p in net.parameters() if p.requires_grad] else: params = net.params norm = torch.sqrt(sum(torch.sum((p.grad ** 2)) for p in params)) if norm > theta: for param in params: param.grad[:] *= theta / norm def train_epoch_ch8(net, train_iter, loss, updater, device, use_random_iter): """训练网络一个迭代周期(定义见第8章)""" state, timer = None, d2l.Timer() metric = d2l.Accumulator(2) # 训练损失之和,词元数量 for X, Y in train_iter: if state is None or use_random_iter: # 在第一次迭代或使用随机抽样时初始化state state = net.begin_state(batch_size=X.shape[0], device=device) else: if isinstance(net, nn.Module) and not isinstance(state, tuple): # state对于nn.GRU是个张量 state.detach_() else: # state对于nn.LSTM或对于我们从零开始实现的模型是个张量 for s in state: s.detach_() y = Y.T.reshape(-1) X, y = X.to(device), y.to(device) y_hat, state = net(X, state) l = loss(y_hat, y.long()).mean() if isinstance(updater, torch.optim.Optimizer): updater.zero_grad() l.backward() grad_clipping(net, 1) updater.step() else: l.backward() grad_clipping(net, 1) # 因为已经调用了mean函数 updater(batch_size=1) metric.add(l * y.numel(), y.numel()) return math.exp(metric[0] / metric[1]), metric[1] / timer.stop() def train_ch8(net, train_iter, vocab, lr, num_epochs, device, use_random_iter=False): """训练模型(定义见第8章)""" loss = nn.CrossEntropyLoss() animator = d2l.Animator(xlabel='epoch', ylabel='perplexity', legend=['train'], xlim=[10, num_epochs]) # 初始化 if isinstance(net, nn.Module): updater = torch.optim.SGD(net.parameters(), lr) else: updater = lambda batch_size: d2l.sgd(net.params, lr, batch_size) predict = lambda prefix: predict_ch8(prefix, 50, net, vocab, device) # 训练和预测 for epoch in range(num_epochs): ppl, speed = train_epoch_ch8( net, train_iter, loss, updater, device, use_random_iter) if (epoch + 1) % 10 == 0: print(predict('time traveller')) animator.add(epoch + 1, [ppl]) print(f'困惑度 {ppl:.1f}, {speed:.1f} 词元/秒 {str(device)}') print(predict('time traveller')) print(predict('traveller')) if __name__ == "__main__": d2l.DATA_HUB['time_machine'] = (d2l.DATA_URL + 'timemachine.txt', '090b5e7e70c295757f55df93cb0a180b9691891a') batch_size, num_steps = 32, 35 train_iter, vocab = p3.load_data_time_machine(batch_size, num_steps) X = torch.arange(10).reshape((2, 5)) num_hiddens = 512 net = RNNModelScratch(len(vocab), num_hiddens, d2l.try_gpu(), get_params, init_rnn_state, rnn) state = net.begin_state(X.shape[0], d2l.try_gpu()) Y, new_state = net(X.to(d2l.try_gpu()), state) num_epochs, lr = 500, 1 train_ch8(net, train_iter, vocab, lr, num_epochs, d2l.try_gpu()) plt.show()
运行结果:
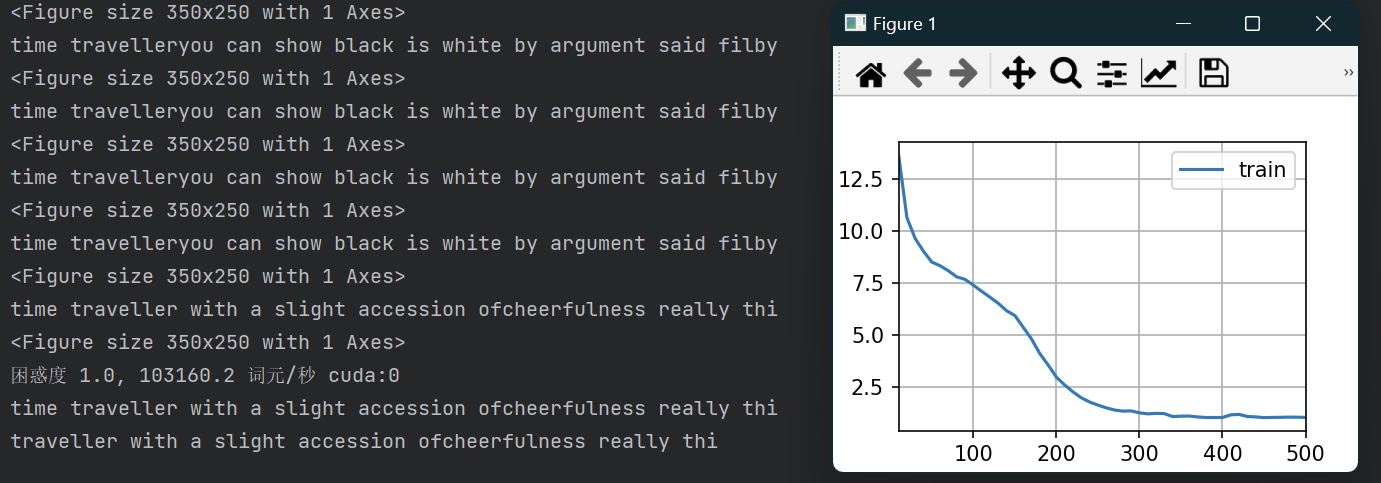




 浙公网安备 33010602011771号
浙公网安备 33010602011771号