李沐动手学深度学习13——现代卷积神经网络

将要学习的现代卷积神经网络包括：

深度卷积神经网络AlexNet、用重复块的网络VGG、网络中的网络NiN、含并行连结的网络GoogLeNet、残差网络ResNet、稠密连接网络DenseNet

一、AlexNet

AlexNet在2012年ImageNet挑战赛中大放异彩，首次证明了学习到的特征可以超越手工设计的特征。

图片3*224*24

——11*11卷积层，通道96，步幅4

——3*3最大汇聚层，步幅2

——5*5卷积层，通道256，填充2

——3*3最大汇聚层，步幅2

——3*3卷积层，通道384，填充1

——3*3卷积层，通道384，填充1

——3*3卷积层，通道256，填充1

——3*3最大汇聚层，步幅2

——全连接层4096

——全连接层4096

——全连接层1000

AlexNet与LeNet的主要差异：1.AlexNet更深，AlexNet比LeNet多3个卷积层。2.AlexNet使用ReLU而不是sigmoid作为激活函数

代码如下;

if __name__ == "__main__":
    net = nn.Sequential(
        # 这里使用一个11*11的更大窗口来捕捉对象。
        # 同时，步幅为4，以减少输出的高度和宽度。
        # 另外，输出通道的数目远大于LeNet
        nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
        nn.MaxPool2d(kernel_size=3, stride=2),
        # 减小卷积窗口，使用填充为2来使得输入与输出的高和宽一致，且增大输出通道数
        nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
        nn.MaxPool2d(kernel_size=3, stride=2),
        # 使用三个连续的卷积层和较小的卷积窗口。
        # 除了最后的卷积层，输出通道的数量进一步增加。
        # 在前两个卷积层之后，汇聚层不用于减少输入的高度和宽度
        nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
        nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
        nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
        nn.MaxPool2d(kernel_size=3, stride=2),
        nn.Flatten(),
        # 这里，全连接层的输出数量是LeNet中的好几倍。使用dropout层来减轻过拟合
        nn.Linear(6400, 4096), nn.ReLU(),
        nn.Dropout(p=0.5),
        nn.Linear(4096, 4096), nn.ReLU(),
        nn.Dropout(p=0.5),
        # 最后是输出层。由于这里使用Fashion-MNIST，所以用类别数为10,而非论文中的1000
        nn.Linear(4096, 10))

 

二、VGG

VGG提供了一个通用的模板来指导后续的研究人员设计新的网络：

一个VGG块包括一系列的卷积层加上用于空间下采样的最大汇聚层，在代码中，我们定义一个vgg_block函数用于实现VGG块：

def vgg_block(num_convs, in_channels, out_channels):
    layers = []
    for _ in range(num_convs):
        layers.append(nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
        layers.append(nn.ReLU())
        in_channels = out_channels
    layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
    return nn.Sequential(*layers)

VGG网络含5个卷积块，前两个块各有一个卷积层，后三个块个包含两个卷积层，共使用8个卷积层和3个全连接层，因此通常称之为VGG11

 

三、NiN

LeNet、AlexNet和VGG都是先通过一系列的卷积层与汇聚层来提取空间结构特征，然后通过全连接层对特征的表征进行处理。

想象在这个过程的早期使用全连接层，可能会失去表征的空间结构。

NiN提供了一种解决方案：在每个像素的通道上分别使用多层感知机，即将单个像素视为一个样本，将通道维度视为特征。

一个NiN块包括一个卷积层，两个1*1卷积层，代码如下：

def nin_block(in_channels, out_channels, kernel_size, strides, padding):
    return nn.Sequential(
        nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
        nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU())

NiN网络包括了四个NiN块，前三个NiN块后接最大汇聚层，最后一个NiN块后接平均汇聚层

 

四、GoogLeNet

GoogLeNet是含并行连结的网络。

GoogLeNet吸收了NiN中串联网络的思想，并在此基础上做了改进，其重点在于解决了什么大小的卷积核最合适的问题。其中的一个观点是，使用不同大小的卷积核组合有时是有利的。

在GoogLeNet中，基本的卷积块被称为Inception块（盗梦空间结构）

Inception块由四条并行路径组成，前三条路径使用窗口大小1*1、3*3和5*5的卷积层，从不同空间大小中提取信息。中间的两条路径在输入上先执行1*1卷积，以减少通道数。第四条路径使用3*3最大汇聚层，然后使用1*1卷积层改变通道数。四条路径使用合适的填充使输入与输出的高和宽相等，最后将每条线路的输出在通道维度上连结，构成Inception块的输出。代码如下：

class Inception(nn.Module):
    def __init__(self, in_channels, c1, c2, c3, c4, **kwargs):
        super(Inception, self).__init__(**kwargs)
        self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)

        self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1)
        self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)

        self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)
        self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)

        self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1)

    def forward(self, x):
        p1 = F.relu(self.p1_1(x))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        return torch.cat((p1, p2, p3, p4), dim=1)

GoogLeNet一共使用9个Inception块和全局平均汇聚层的堆叠来生成其估计值，第一、二个模块类似于AlexNet、LeNet和VGG块，创建一个GoogLeNet网络代码如下：

    b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                       nn.ReLU(),
                       nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

    b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1),
                       nn.ReLU(),
                       nn.Conv2d(64, 192, kernel_size=3, padding=1),
                       nn.ReLU(),
                       nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

    b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
                       Inception(256, 128, (128, 192), (32, 96), 64),
                       nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

    b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
                       Inception(512, 160, (112, 224), (24, 64), 64),
                       Inception(512, 128, (128, 256), (24, 64), 64),
                       Inception(512, 112, (144, 288), (32, 64), 64),
                       Inception(528, 256, (160, 320), (32, 128), 128),
                       nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

    b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
                       Inception(832, 384, (192, 384), (48, 128), 128),
                       nn.AdaptiveAvgPool2d((1, 1)),
                       nn.Flatten())

    net = nn.Sequential(b1, b2, b3, b4, b5, nn.Linear(1024, 10))

 

五、批量规范化

批量规范化是一种加速深层网络收敛速度的技术。

在之前使用多层感应机的案例中，第一步是标准化输入特征，使其平均值为0，方差为1，从而加快收敛速度。

在训练神经网络时，中间层的变量可能有更广的变化范围，随着时间推移，模型参数随着训练更新而变幻莫测。批量规范化的发明者非正式地假设，这些变量分布中的这种偏移可能会阻碍网络的收敛，更直观地说，如果一个层的可变值是另一层的100倍，可能会需要对学习率进行补偿调整。

而深层网络更加复杂，更容易过拟合，因此正则化更加重要。

批量规范化可以应用于单个可选层，也可以应用到所有层，其原理如下：每次训练迭代中，首先规范化输入，即减去均值并除以其标准差，其中两者均基于当前处理的小批量数据，然后，应用比例系数和比例偏移。

什么是拉伸和偏移，该步骤的意义是什么：数据被标准化后，可能会降低模型的灵活性、或损失信息，为了弥补标准化的局限性，引入两个可学习的参数：拉伸和偏移，处理标准化后的数据。

全连接层和卷积层的批量规范化实现略有不同。

对于全连接层，将批量规范化置于仿射变换和激活函数之间。

对于卷积层，将批量规范化置于卷积层与非线性激活函数之间，当卷积层有多个通道时，在各个通道上独立地计算方差和均值，每个通道上的拉伸和偏移参数同样独立。

批量规范化层代码如下：

def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
    """
    :param gamma: 拉伸参数
    :param beta: 偏移参数
    :param moving_mean: 全局均值
    :param moving_var: 全局方差
    :param eps: 防止分母为0的较小值，可取1e-5
    :param momentum: 动量参数，用于更新moving_mean和moving_var
    :return:
    """
    if not torch.is_grad_enabled():
        X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
    else:
        # 仅支持全连接或卷积层输入（维度为2或4）
        assert len(X.shape) in (2, 4)
        if len(X.shape) == 2:
            # 沿batch维度计算每个特征的均值和方差
            mean = X.mean(dim=0)
            var = ((X - mean) ** 2).mean(dim=0)
        else:
            # 卷积层的输出是4维的（位次，通道，长，宽）
            # 在通道维度上求均值,比如原数据形状为（2,3,2,2）,求均值后，为（1,3,1,1）,相当于结果只有三个数值, 但是维度不变
            mean = X.mean(dim=(0, 2, 3), keepdim=True)
            var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
        # 标准化数据
        X_hat = (X - mean) / torch.sqrt(var + eps)
        # 使用指数移动平均的方法求模型的均值和方差
        moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
        moving_var = momentum * moving_var + (1.0 - momentum) * var
    # 应用平移和拉伸
    Y = gamma * X_hat + beta
    return Y, moving_mean.data, moving_var.data


class BatchNorm(nn.Module):
    # num_features: 完全连接层的输出数量或卷积层的输出通道数
    # num_dims: 2表示完全连接层，4表示卷积层
    def __init__(self, num_features, num_dim):
        super().__init__()
        if num_dim == 2:
            shape = (1, num_features)
        else:
            shape = (1, num_features, 1, 1)
        self.gamma = nn.Parameter(torch.ones(shape))
        self.beta = nn.Parameter(torch.zeros(shape))
        self.moving_mean = torch.zeros(shape)
        self.moving_var = torch.ones(shape)

    def forward(self, X):
        if self.moving_mean.device != X.device:
            self.moving_mean = self.moving_mean.to(X.device)
            self.moving_var = self.moving_var.to(X.device)
        Y, self.moving_mean, self.moving_var = batch_norm(
            X, self.gamma, self.beta, self.moving_mean,
            self.moving_var, eps=1e-5, momentum=0.9)
        return Y

 

 六、残差网络

思想与原理：在架构方面进行学习，同时新架构包含旧架构以保证不断向目标近似，通过将新添加的层训练为恒等映射，使新模型与旧模型同样有效，使得新模型可能得出更优的解来拟合训练数据集。

实现：ResNet沿用了VGG的设计，残差块里首先有两个相同输出通道数的3*3卷积层，每个卷积层后接一个批量规范化层和ReLu激活函数。然后通过跨层数据通路，将输入直接加到最后的ReLU激活函数前。如果想改变通道数，需要二外引入一个1*1卷积层变换输入形状后再做相加运算：

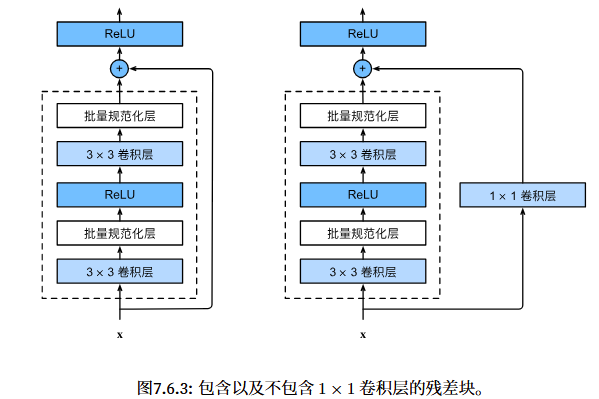
 实现代码如下：

class Residual(nn.Module):
    def __init__(self, input_channels, num_channels, use_1x1conv=False, strides=1):
        """
        :param use_1x1conv: 是否需要额外卷积层
        :param strides: 步幅
        """
        super().__init__()
        self.conv1 = nn.Conv2d(input_channels, num_channels, kernel_size=3, padding=1, stride=strides)
        self.conv2 = nn.Conv2d(num_channels, num_channels, kernel_size=3, padding=1)
        if use_1x1conv:
            self.conv3 = nn.Conv2d(input_channels, num_channels, kernel_size=1, stride=strides)
        else:
            self.conv3 = None
        self.bn1 = nn.BatchNorm2d(num_channels)
        self.bn2 = nn.BatchNorm2d(num_channels)
    
    def forward(self, X):
        Y = F.relu(self.bn1(self.conv1(X)))
        Y = self.bn2(self.conv2(Y))
        if self.conv3:
            X = self.conv3(X)
        Y += X
        return F.relu(Y)

ResNet模型：ResNet与GoogLeNet类似，前两层在输出通道数为64、步幅为2的7 × 7卷积层后，接步幅为2的3 × 3的最大汇聚层。不同之处在于ResNet每个卷积层后增加了批量规范化层。GoogLeNet在后面接了4个由Inception块组成的模块。ResNet则使用4个由残差块组成的模块，每个模块使用若干个同样输出通道数的残差块。第一个模块的通道数同输入通道数一致。由于之前已经使用了步幅为2的最大汇聚层，所以无须减小高和宽。之后的每个模块在第一个残差块里将上一个模块的通道数翻倍，并将高和宽减半。

 

七、DenseNet

稠密连接网络，某种程度上是ResNet的逻辑扩展。ResNet是将x与f(x)相加，而DenseNet是将x与f(x)连接，DenseNet的稠密块代码如下：

def conv_block(input_channels, num_channels):
    return nn.Sequential(
        nn.BatchNorm2d(input_channels), nn.ReLU(),
        nn.Conv2d(input_channels, num_channels, kernel_size=3, padding=1)
    )


class DenseBlock(nn.Module):
    def __init__(self, num_convs, input_channels, num_channels):
        super(DenseBlock, self).__init__()
        layer = []
        for i in range(num_convs):
            layer.append(conv_block(num_channels * i + input_channels, num_channels))
        self.net = nn.Sequential(*layer)

    def forward(self, X):
        for blk in self.net:
            Y = blk(X)
            X = torch.cat((X, Y), dim=1)
        return X


def transition_block(input_channels, num_channels):
    return nn.Sequential(
        nn.BatchNorm2d(input_channels), nn.ReLU(),
        nn.Conv2d(input_channels, num_channels, kernel_size=1),
        nn.AvgPool2d(kernel_size=2, stride=2))