相机标定原理介绍（一）

http://blog.csdn.net/aptx704610875/article/details/48914043标定实例

 

一.总体原理：

摄像机标定(Camera calibration)简单来说是从世界坐标系换到图像坐标系的过程，也就是求最终的投影矩阵的过程。

[1]基本的坐标系：

• 世界坐标系；
• 相机坐标系；
• 成像平面坐标系；
• 像素坐标系

[2]一般来说，标定的过程分为两个部分：

• 第一步是从世界坐标系转为相机坐标系，这一步是三维点到三维点的转换，包括R，t（相机外参，确定了相机在某个三维空间中的位置和朝向）等参数；
• 第二部是从相机坐标系转为成像平面坐标系（像素坐标系），这一步是三维点到二维点的转换，包括K（相机内参,是对相机物理特性的近似）等参数；
• 投影矩阵 ： P=K [ R | t ]    是一个3×4矩阵，混合了内参和外参而成。
  
  P=K[Rt]

 

二.基本知识介绍及

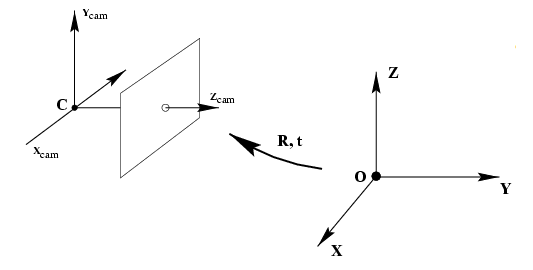
1、摄像机模型

Pinhole Camera模型如下图所示：

 

 是一个小孔成像的模型，其中：

  [1]O点表示camera centre，即相机的中心点，也是相机坐标系的中心点；

  [2]z轴表示principal axis，即相机的主轴；

  [3]q点所在的平面表示image plane，即相机的像平面，也就是图片坐标系所在的二维平面；

  [4]O1点表示principal point，即主点，主轴与像平面相交的点；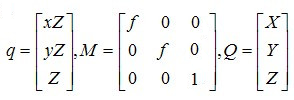

  [5]O点到O1点的距离，也就是右边图中的f,即相机的焦距；

  [6]像平面上的x和y坐标轴是与相机坐标系上的X和Y坐标轴互相平行的；

  [7]相机坐标系是以X,Y,Z（大写）三个轴组成的且原点在O点，度量值为米（m）；

  [8]像平面坐标系是以x,y（小写）两个轴组成的且原点在O1点，度量值为米（m）；

  [9]像素坐标系一般指图片相对坐标系，在这里可以认为和像平面坐标系在一个平面上，不过原点是在图片的角上，而且度量值为像素的个数（pixel）；

 

2、相机坐标系→成像平面坐标系

[1]以O点为原点建立摄像机坐标系。点Q(X,Y,Z)为摄像机坐标系空间中的一点，该点被光线投影到图像平面上的q(x,y,f)点。

图像平面与光轴z轴垂直，和投影中心距离为f （f是相机的焦距）。按照三角比例关系可以得出：

x/f = X/Z       y/f = Y/Z   ，即 x = fX/Z       y = fY/Z

以上将坐标为(X,Y,Z)的Q点映射到投影平面上坐标为(x,y)的q点的过程称作投影变换。

上述Q点到q点的变换关系用3*3的矩阵可表示为：q = MQ ，其中

  
    最终得出透视投影变换矩阵为：

（1）

M称为摄像机的内参数矩阵，单位均为物理尺寸。

(X,Y,Z)↦(fX/Z,fY/Z)

(X,Y,Z)↦(fX/Z,fY/Z)

通过上面，可以把相机坐标系转换到像图像坐标系的物理单位[即(X,Y,Z)→(x,y)]

3、成像平面坐标系→像素坐标系

通过下面，可以把像平面坐标系物理单位到像素单位[即→(u,v)]

 

以图像平面的左上角或左下角为原点建立坐标系。假设像平面坐标系原点位于图像左下角，水平向右为u轴，垂直向上为v轴，均以像素为单位。

以图像平面与光轴的交点O₁ 为原点建立坐标系，水平向右为x轴，垂直向上为y轴。原点O₁一般位于图像中心处，O₁在以像素为单位的图像坐标系中的坐标为(u_0, v₀)。

像平面坐标系和像素坐标系虽然在同一个平面上，但是原点并不是同一个。

设每个像素的物理尺寸大小为 dx * dy (mm) ( 由于单个像素点投影在图像平面上是矩形而不是正方形，因此可能dx != dy)，

图像平面上某点在成像平面坐标系中的坐标为(x, y)，在像素坐标系中的坐标为(u, v)，则二者满足如下关系：[即(x, y)→(u, v)]

u = x / dx + u₀            v = y / dy +  v₀

用齐次坐标与矩阵形式表示为：

 将等式两边都乘以点Q(X,Y,Z)坐标中的Z可得：

 将摄像机坐标系中的（1）式代入上式可得：

  则右边第一个矩阵和第二个矩阵的乘积亦为摄像机的内参数矩阵（单位为像素），相乘后可得：

（2）

 和（1）式相比，此内参数矩阵中f/dx, f/dy,  c_x/dx+u0, c_y/dy+v0  的单位均为像素。令内参数矩阵为K，则上式可写成：

（3）

三.相机内参K（与棋盘所在空间的3D几何相关）

 

在计算机视觉中，摄像机内参数矩阵

其中 f 为摄像机的焦距，单位一般是mm;dx,dy 为像元尺寸;u₀,v₀ 为图像中心。

fx = f/dx, fy = f/dy,分别称为x轴和y轴上的归一化焦距.

 

为更好的理解，举个实例：

现以NiKon D700相机为例进行求解其内参数矩阵：
就算大家身边没有这款相机也无所谓，可以在网上百度一下，很方便的就知道其一些参数——      
  焦距 f = 35mm   最高分辨率：4256×2832     传感器尺寸：36.0×23.9 mm
根据以上定义可以有：
u₀= 4256/2 = 2128   v₀= 2832/2 = 1416  dx = 36.0/4256   dy = 23.9/2832
fx = f/dx = 4137.8   fy = f/dy = 4147.3

分辨率可以从显示分辨率与图像分辨率两个方向来分类。
[1]显示分辨率（屏幕分辨率）是屏幕图像的精密度，是指显示器所能显示的像素有多少。由于屏幕上的点、线和面都是由像素组成的，

显示器可显示的像素越多，画面就越精细，同样的屏幕区域内能显示的信息也越多，所以分辨率是个非常重要的性能指标之一。

可以把整个图像想象成是一个大型的棋盘，而分辨率的表示方式就是所有经线和纬线交叉点的数目。

显示分辨率一定的情况下，显示屏越小图像越清晰，反之，显示屏大小固定时，显示分辨率越高图像越清晰。
[2]图像分辨率则是单位英寸中所包含的像素点数，其定义更趋近于分辨率本身的定义。

 四.畸变参数（与点集如何畸变的2D几何相关。）

采用理想针孔模型，由于通过针孔的光线少，摄像机曝光太慢，在实际使用中均采用透镜，可以使图像生成迅速，但代价是引入了畸变。

有两种畸变对投影图像影响较大： 径向畸变和切向畸变。

1、径向畸变
对某些透镜，光线在远离透镜中心的地方比靠近中心的地方更加弯曲，产生“筒形”或“鱼眼”现象，称为径向畸变。

一般来讲，成像仪中心的径向畸变为0，越向边缘移动，畸变越严重。不过径向畸变可以通过下面的泰勒级数展开式来校正：

x_corrected = x(1+k₁r²+k₂r⁴+k₃r⁶)

y_corrected = y(1+k₁r²+k₂r⁴+k₃r⁶)

这里（x, y）是畸变点在成像仪上的原始位置，r为该点距离成像仪中心的距离，（x_{corrected ，}y_corrected ）是校正后的新位置。

对于一般的摄像机校正，通常使用泰勒级数中的前两项k₁和k₂就够了；对畸变很大的摄像机，比如鱼眼透镜，可以使用第三径向畸变项k₃

2、切向畸变

当成像仪被粘贴在摄像机的时候，会存在一定的误差，使得图像平面和透镜不完全平行，从而产生切向畸变。也就是说，如果一个矩形被投影到成像仪上时，

可能会变成一个梯形。切向畸变可以通过如下公式来校正：

x_corrected = x + [ 2p₁y + p₂ (r² + 2x²) ]

y_corrected = y + [ 2p₂x + p₁ (r² + 2y²) ]

这里（x, y）是畸变点在成像仪上的原始位置，r为该点距离成像仪中心的距离，（x_{corrected ，}y_corrected ）是校正后的新位置。

 

 

五.摄像机的外参数

旋转向量（大小为1×3的矢量或旋转矩阵3×3）和平移向量（tx,ty,tz）。

旋转向量:旋转向量是旋转矩阵紧凑的变现形式，旋转向量为1×3的行矢量。

 r就是旋转向量，旋转向量的方向是旋转轴 ,旋转向量的模为围绕旋转轴旋转的角度。

通过上面的公式，我们就可以求解出旋转矩阵R。同样的已知旋转矩阵，我们也可以通过下面的公式求解得到旋转向量：

六.思考

 

那为什么要做相机标定呢？

【1】进行摄像机标定的目的：求出相机的内、外参数，以及畸变参数。
【2】标定相机后通常是想做两件事：一个是由于每个镜头的畸变程度各不相同，通过相机标定可以校正这种镜头畸变矫正畸变，生成矫正后的图像；另一个是根据获得的图像重构三维场景。

      摄像机标定过程，简单的可以简单的描述为通过标定板，如下图，可以得到n个对应的世界坐标三维点X_i和对应的图像坐标二维点x_i，这些三维点到二维点的转换都可以通过上面提到的相机内参K，相机外参R和t，以及畸变参数D，经过一系列的矩阵变换得到。

 

七.标定内幕过程的分析：

1.假设有N个角点和K个棋盘图像（不同位置），需要多少个视场和角点才能提供足够的约束来求解这些参数呢？

K个棋盘，可以提供2NK的约束，即2NK的方程。（乘以2是因为每个点都由x和y两个坐标值组成）

忽略每次的畸变，那么我们需要求解4个内参数和6K个外参数。（因为对于不同的视场，6个外参数是不同的）

那么有解的前提是方程的总数应该大于等于未知参数的总数即2NK>=6K+4,或者写成(N-3)K>=2。

为了方便理解，下图是一个3×3大小的棋盘,红色圈标记出了它含有的内角点：

如果我们令N=5,K=1，带入到上述不等式，是满足不等式，这就是意味着我们仅需要一个视场和带有5个内角点的棋盘就可以求解出10个参数了。其实不然，为了描述投影视场的所有目标只需要4个点，即一次性在四个方向上延展正方形的边，把它变成任意四边形。因此，无论一个平面上检测到多少个角点，我们只能得到4个有用的角点信息。如上图所示是一个3×3大小的棋盘，有4个内角点。对于每一个视场，我们仅能给出4个有用的角点信息，那么上述的公式中N就约束为4，即公式变为(4-3)K>=2，即K>=2。即要求解10个参数最少需要两个视场。考虑到噪声和数值稳定性要求，对大棋盘需求收集更多的图像。为了得到高质量结果，至少需要10幅7×8或者更大棋盘的图像（而且只在移动棋盘在不同图像中足够大以从视场图像中得到更加丰富的信息）。

2.数学是怎么应用于标定的？

OpenCV选着那些能够很好工作于平面物体的方法。OpenCV中使用的求解焦距和偏移的算法是基于张的方法，但求解畸变参数则是另外一个基于Brown的方法。

(1)首先我们假定求解标定参数时，摄像机没有畸变。对于每一个棋盘视场，我们得到一个前面描述的单应性矩阵H，大小为3×3。将H写成列向量的形式，即H=[h1 h2 h3]，每个h是3×1向量，单应性矩阵H是物理变换（旋转、平移）和相机内参数组成。我们的目的就是分解这个H，能够从中分解出这些成分。

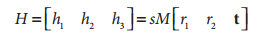
M是摄像机内参数矩阵，r1,r2是旋转矢量3×1，t是平移矢量，缩放因子s，对应项相等得到如下：

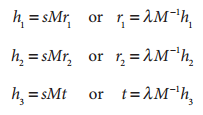          λ=1/s

我们知道R=[r1,r2,r3]，r3消失，是因为我们另Z=0。R是一个正交阵，即R的转置等于R的逆。正交阵的每个列向量是两两正交且单位化的（即模为1）,那么r1和r2是相互正交。

正交的含义有两个：两个矢量的点积为0，两个矢量的长度相等。下面我们就用这两个约束来进行求解。

我们将r1和r2带入到上述的公式得：

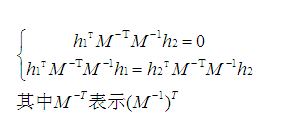
令：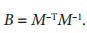

展开有：

 

其中M公式如下：

（注意：这里的c_x、Cy相当于上面的_U0、V0）

将M带入公式，可以得到矩阵B的通用形式的封闭解：

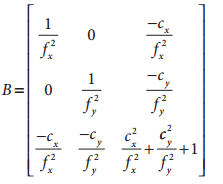
这里重新写一下两个约束：

由于B是对称真，那么B可以仅有对角线下半元素或者对角线上半元素表示，即可以有6个元素表示。我们将通用形式展开，并且提取出B成分，那么通用形式可以写成含有旋转成分和含有B成分的6个元素组成的向量的点积（注意：是点积，不是两个矩阵相乘），如下：

从上述公式，我们已知单应性矩阵H,那么它其中的每一个元素我们都是已知的，那么上述Bij是我们要求解的值，

我们可以组合两个约束为如下的形式：

每一个视场我们可以得到形如上面描述的2个公式（上述黄色部分），那么对于K的视场，我们可以得到2K个这样的公式。

我们堆积这些方程有：

b是要求解未知数矢量大小为6×1，V是2K×6的矩阵，如果K>=2，那么方程有解b=[B11,B12,B22,B13,B23,B33]T。摄像机内参数可以从B矩阵的封闭解中直接得到：

外参数（旋转和平移）可以由单应性条件计算得到：

上述公式中，λ,M,H,都是求解的得到的作为已知量，（r3=r1×r2，这是因为r1,r2,r3两两正交）。

需要小心的是，当我们使用真实的数据求解时，将计算得到的r向量放在一起（R=(r1,r2,r3)），我们并不能得到精确的旋转矩阵R，使得R为正交阵。

为了解决这个问题，我们常使用强制的方法，即对R进行奇异值分解，R=UDVT，U，V为正交阵，D为对角阵，如果R是正交阵，那么奇异值分解后的对角阵D是单位阵，那么我们将单位阵I代替对角阵D,进而重构出满足正交条件的R.

(2)在前面的工作中，我们总是先忽略透镜畸变，然后求解得到的系统。如果针孔模型是完美的，令（xp,yp）为点的位置，令(xd,yd)为畸变的位置，那么有：

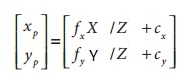
通过下面的替换，可以得到没有畸变的标定结果：

就像先前描述的那样，上述5个畸变参数：k1,k2,k3,p1,p2，需要3个角点构成的6组方程就可以求解。我们猜测一下，我们通过前面的计算已经求解出相机的内参数:fx,fy,cx,cy，棋盘平面上角点的坐标为世界坐标，其中X,Y我们可以理解为在其平面上的坐标，Z是一个尺度，因为我们知道求解单应性矩阵H，也是一个尺度，所以具体怎么控制，先不用管，我们就可以通过上述公式一求解出xp和yp，xd,yd就是成像仪上角点的真实位置，那么就可以由xp,yp和xd,yd的点对，带入到上述的公式二，求可以求解出5个畸变系数。

备注：

齐次坐标
就是将一个原本是n维的向量用一个n+1维向量来表示。
许多图形应用涉及到几何变换，主要包括平移、旋转、缩放。以矩阵表达式来计算这些变换时，平移是矩阵相加，旋转和缩放则是矩阵相乘，综合起来可以表示为x=R*X+t (注：因为习惯的原因，实际使用时一般使用变化矩阵左乘向量）(R 旋转缩放矩阵，t 为平移矩阵，X 为原向量，x 为变换后的向量)。

引入齐次坐标的目的主要是合并矩阵运算中的乘法和加法，表示为x=P*X的形式。即它提供了用矩阵运算把二维、三维甚至高维空间中的一个点集从一个坐标系变换到另一个坐标系的有效方法。和上面的计算过程是对应的。