柏林噪声

　然后我们来讨论一下一维、二维柏林噪声的原理。
1、一维柏林噪声
　　首先，在X轴向上每个整数坐标随机生成一个数（范围为-1~1），我们称这个数为Gradient，译为梯度或者斜率。然后我们对相邻两个整数之间使用梯度进行插值计算，使得相邻两点之间平滑过渡。平滑度取决于所选用的插值函数，老版的柏林噪声使用f(t)= 3 * t * t-2 * t * t * t，改进后的柏林噪声使用f(t)=t * t * t * (t * (t * 6-15)+10)。
　　如图所示：

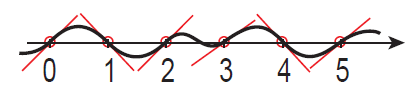
　　上图来自于KenPerlin的Simplex Noise论文，论文中提到了经典的柏林噪声定义。
2、二维柏林噪声
　　对于二维来说我们可以获取点P(x, y)最近的四个整数点ABCD，ABCD四个点的坐标分别为A(i, j)、B(i+1, j)、C(i, j+1)、D(i+1, j+1)，随后获取ABCD四点的二维梯度值G(A)、G(B)、G(C)、G(D)，并且算出ABCD到P点的向量AP、BP、CP以及DP。如下图所示：

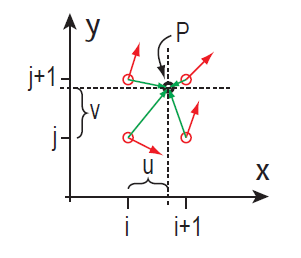
　　红色箭头表示该点处的梯度值，绿色箭头表示该点到P点的向量。
　　接着，将G(A)与AP进行点乘，计算出A点对于P点的梯度贡献值，然后分别算出其余三个点对P点的梯度贡献值，最后将(u, v)代入插值函数中算出P点的最终噪声值。
　　以上类推到三维的柏林噪声，则需要算出八个顶点的梯度贡献值，然后进行插值计算。
　　还有一个问题没有解决，就是怎样随机生成梯度值。当然你可以通过使用一个伪随机函数生成一维到三维的梯度值（二维和三维就是梯度向量了），例如，对于一维可以使用下面的公式：
　　Fract(Sin(n)753.5453123f);
　　另外一种，也是柏林使用的，是预先生成256个伪随机的梯度值（以及二维和三维的梯度向量）保存在G1[256]、G2[256][2]]以及G3[256][3]中，然后对于一维柏林噪声来说，我们可以直接去取G1[]数组中的梯度值使用，对于二维或者三维的怎么办？柏林预先又生成了一个排列P[256]，将0~255的下标随机存放在P数组中，然后通过下面公式来取到随机的梯度值：
　　G2[P[x] + y] ——二维
　　G3[P[P[x] + y] +z] ——三维
　　以上就完成了随机取梯度值的算法。
　　当然，这里还要提一下在Improved Noise论文中柏林对于三维柏林噪声的改进。在论文中柏林的第一个改进就是插值函数的改进，也就是我们上面提到过的f(t)=ttt(t(t6-15)+10)，它使得插值出来的噪声值更平滑了，特别是在三维中。

引用：
https://gameinstitute.qq.com/community/detail/106827