计算几何学习笔记(一):二维计算几何
平面几何基本知识
这部分是小学 / 初中 / 高中知识。
平面直角坐标系:在同一个平面上互相垂直且有公共原点 \(O\) 的两条数轴 \(x, y\) 构成平面直角坐标系。
对于平面内任意一点 \(A\),过点 \(A\) 分别向 \(x\) 轴、\(y\) 轴作垂线,垂足在 \(x\) 轴、\(y\) 轴上的对应点 \(a, b\) 分别叫做点 \(A\) 的横坐标、纵坐标,有序数对 \((a, b)\) 叫做点 \(A\) 的直角坐标。
平面极坐标系:在平面上选一定点 \(O\),称为极点;
自极点引出一条射线 \(Ox\),称为极轴;
选择一个单位长度(在数学问题中通常为 \(1\)),一个角度单位(通常为弧度)及其正方向(通常为逆时针方向);
就建立了极坐标系。
设 \(A\) 为平面上一点。
-
极点 \(O\) 与 \(A\) 之间的距离 \(|OA|\) 称为极径,记为 \(\rho\);
-
以极轴为始边,\(OA\) 为终边的角 \(\angle xOA\) 称为极角,记为 \(\varphi\)。
那么有序数对 \((\rho,\varphi)\) 即为 \(A\) 的极坐标。
点积:不用矩阵表示。已知两个向量 \(\boldsymbol a, \boldsymbol b\),它们的夹角为 \(\theta\),那么它们的点积 \(\boldsymbol a \cdot \boldsymbol b = |\boldsymbol a||\boldsymbol b| \cos \theta\)。
叉积:不用矩阵表示。已知两个向量 \(\boldsymbol a, \boldsymbol b\),它们的夹角为 \(\theta\),那么它们的叉积 \(\boldsymbol a \times \boldsymbol b = |\boldsymbol a||\boldsymbol b| \sin \theta\)。
点与直线基础问题
接下来的知识和高中数学有所不同,信息学更喜欢用向量来计算。
判断向量夹角关系
根据 \(\cos\) 的性质,可以判断两个向量 \(\boldsymbol a\) 和 \(\boldsymbol b\) 的夹角关系:
-
\(\boldsymbol a \cdot \boldsymbol b = 0\),两向量垂直;
-
\(\boldsymbol a \cdot \boldsymbol b < 0\),夹角小于 \(90^{\circ}\);
-
\(\boldsymbol a \cdot \boldsymbol b > 0\),夹角大于 \(90^{\circ}\)。
判断向量位置关系
根据 \(\sin\) 的性质,可以判断两个向量 \(\boldsymbol a\) 和 \(\boldsymbol b\) 的位置关系:
-
\(\boldsymbol a \times \boldsymbol b = 0\),两向量共线;
-
\(\boldsymbol a \times \boldsymbol b < 0\),\(\boldsymbol b\) 在 \(\boldsymbol a\) 的顺时针方向;
-
\(\boldsymbol a \times \boldsymbol b > 0\),\(\boldsymbol b\) 在 \(\boldsymbol a\) 的逆时针方向。
向量旋转
假设我们要将 \(\boldsymbol v = (a, b)\) 逆时针旋转 \(\theta\) 度。根据向量的三角表示的运算,可以得到旋转后的向量 \(\boldsymbol v' = (a \cos \theta - b \sin \theta, b \cos \theta + a \sin \theta)\)。
判断线段是否相交
首先特判一些特殊情况。如果两线段平行,自然不能相交。这种情况通过判断线段所在直线的斜率是否相等即可。
对于其他情况,我们先介绍以下这种判断方法。
快速排斥实验:规定「一条线段的区域」为以这条线段为对角线的,各边均与某一坐标轴平行的矩形所占的区域,那么可以发现,如果两条线段没有公共区域,则这两条线段一定不相交。
注意到如果两条线段有公共区域,它们也有可能不相交,因此还有另一种判断直线是否相交的办法。
跨立实验:如果对于两线段 \(AB, CD\),\(CD\) 线段的两个端点分布在 \(AB\) 线段所在直线的两侧,且 \(AB\) 线段的两个端点分布在 \(CD\) 线段所在直线的两侧,我们就称即两线段相交。
具体的,我们从 \(A\) 的向 \(C\) 和 \(D\) 的各连一条线段,再将其看成向量。如果 \(\overrightarrow{AC} \times \overrightarrow{AB}\) 与 \(\overrightarrow{AD} \times \overrightarrow{AB}\) 异号,那么就可以说明 \(C\) 和 \(D\) 在 \(AB\) 两侧。
注意到当两条线段共线但不相交时也可以通过跨立实验,但是这样就不能通过快速排斥实验。因此如果两条线段既通过了快速排斥实验,又通过了跨立实验,那么这两条直线就相交了。
求线段交点
设 \(AB, CD\) 交于点 \(E\),那么 \(\overrightarrow{OE} = \overrightarrow{OA} + \displaystyle\frac{\overrightarrow{AC} \times \overrightarrow{CD}}{\overrightarrow{CD} \times \overrightarrow{AB}} \times \overrightarrow{AB}\),通过等面积法可以得证。
注意:如果两线段不交,这个式子也会返回它们所在直线的交点,此时需要通过上一小节的知识特判。
还有一点,如果 \(\overrightarrow{AB}\) 和 \(\overrightarrow{CD}\) 共线,那么分母会变成 \(0\),此时也需要特判。
点击查看代码
Point Intersection(Line a, Line b){
Vector x = a.t - a.s, y = b.t - b.s, z = a.s - b.s;
return a.s + x * (Cross(y, z) / Cross(x, y));
}
判断点是否在直线左侧
点到线段的距离
假设我们要求点 \(C\) 到线段 \(AB\) 的距离。首先,如果 \(\triangle ABC\) 是钝角三角形且 \(C\) 为锐角顶点,那么 \(C\) 到线段 \(AB\) 的距离就是 \(\min(AC, BC)\),需要特判。
接下来,依然使用等面积法,根据叉积的几何含义,可以得到 \(d = \displaystyle\frac{|\overrightarrow{AC} \times \overrightarrow{BC}|}{|\overrightarrow{AB}|}\)。
点到直线的垂足
设过 \(C\) 往 \(AB\) 作垂线垂足为 \(H\)。根据点积的几何含义,可以得到 \(\overrightarrow{AH} = \displaystyle\frac{|\overrightarrow{AC} \cdot \overrightarrow{AB}|}{|AB|^2} \overrightarrow{AB}\)。
多边形基础问题
多边形周长
直接计算即可。
多边形面积
设多边形顶点按顺时针排列为:\(\boldsymbol{a_1} = (x_1, y_1), \boldsymbol{a_2} = (x_2, y_2), \dots, \boldsymbol{a_n} = (x_n, y_n)\),那么这个多边形的面积 \(S = \displaystyle\frac 12 \left(\boldsymbol{a_n} \times \boldsymbol{a_1} + \sum_{i = 1}^{n - 1} \boldsymbol{a_i} \times \boldsymbol{a_{i + 1}} \right)\)。
证明:
点击查看代码
double area(){
n = p.size();
double res = 0;;
for(int i = 0; i < n; i++)
res += (Cross(p[i], p[(i + 1) % n]));
res /= 2;
return res;
}
判断点在多边形内
一个可以感性理解的方法。我们考虑以该点为端点引出一条射线,如果这条射线与多边形有奇数个交点,则该点在多边形内部,否则该点在多边形外部。根据若尔当曲线定理,这条射线每次与多边形的一条边相交,就切换一次与多边形的内外关系,所以统计交点数的奇偶就可以了。
点击查看代码
判断点在凸多边形内
此时的多边形变成了凸的,此时我们就有了更简单的方法。
一个非常简单的思路为,我们直接花费 \(\mathcal O(n)\) 的时间复杂度,枚举凸包上的每条边,用叉积判断这个点是否在该边的左侧。
还有一种方法是,钦定一个顶点,二分出它可能在以这个顶点为顶点,多边形上的边为底边的哪个三角形内,看它是否在那条边左侧即可。不过值得注意的是,它可能不在任何一个三角形中,需要特判。
点击查看代码
bool inco(Point A, vector <Point> &a){
int l = 0, r = a.size() - 1;
while(l < r){
int mid=(l + r + 1) >> 1;
if(sgn(Cross(a[mid] - a[0], A - a[0])) >= 0)
l = mid;
else
r = mid - 1;
}
if(l == (int)a.size() - 1){
if(sgn(Cross(A - a[0], A - a[l])) == 0 && sgn(a[0].x - A.x) <= 0 && sgn(A.x - a[l].x) <= 0 && sgn(a[0].y - A.y) <= 0 && sgn(A.y - a[l].y) <= 0)
return 1;
return 0;
} else if(Cross(a[l + 1] - a[l], A - a[l]) >= 0)
return 1;
else
return 0;
}
经典例题
洛谷 P4468 [SCOI2007] 折纸
洛谷 P4529 [SCOI2003] 切割多边形
距离
欧几里得距离
曼哈顿距离
切比雪夫距离
三角剖分
自适应辛普森法
自适应辛普森法是一种精度比较高的拟合积分的方法。
一般我们求积分都是通过矩形去拟合,如图所示:
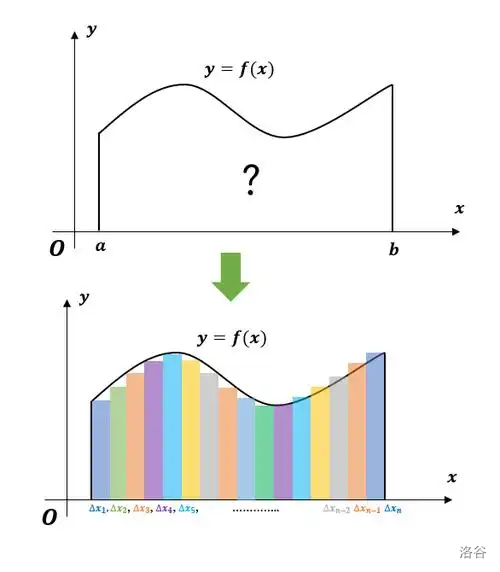
但是经过大量的实验(?),我们发现如果在计算机上使用这种方法去求积分,精度比较低,因此我们发扬人类智慧,用二次函数去拟合原函数。
首先,我们根据多项式的积分,可以得到 \(\displaystyle\int ax^2 + bx + c \mathrm dx = \frac a3 x^3 + \frac b2 x^2 + cx + C\),我们将其设为 \(g(x)\),表示该二次函数下的面积。
和用矩形去拟合函数一样,我们将 \([l, r]\) 分成若干个小区间,每个小区间用二次函数拟合原函数 \(f(x)\) 在这一区间下的面积,再求和,可以得到 \(\displaystyle\int_l^r g(x) \mathrm dx = \int_l^r \frac a3 x^3 + \int_l^r \frac b2 x^2 + \int_l^r cx = \frac{a (r^3 - l^3)}{3} + \frac{b (r^2 - l^2)}{2} + c(r - l)\)。
不过我们发现这个式子似乎和 \(g(x)\) 没有太大关系,因此我们胡乱化简,看看能不能在分子处凑出 \(g(x)\) 的形式,结果还真化简成功了:\(\displaystyle\frac{a (r^3 - l^3)}{3} + \frac{b (r^2 - l^2)}{2} + c(r - l) = \frac{(r - l) \left[a l^2 + bl + c + a r^2 + br + c + 4 \left(\frac{a l^2 + 2alr + a r^2}{4} + \frac{bl + br}{2} + c\right) \right]}{6} = \frac{(r - l) \left[g(l) + g(r) + 4 g \left(\frac{l + r}{2} \right) \right]}{6}\)。
由于我们是用 \(g(x)\) 来拟合 \(f(x)\),因此 \(g(x) \approx f(x)\),因此 \(\displaystyle\frac{(r - l) \left[g(l) + g(r) + 4 g \left(\frac{l + r}{2} \right) \right]}{6} \approx \frac{(r - l) \left[f(l) + f(r) + 4 f \left(\frac{l + r}{2} \right) \right]}{6}\),也就是 \(f(x)\) 在 \([l, r]\) 这一段的近似积分啦。
但是这样精度还是不够,因此我们不断将 \([l, r]\) 拆分成 \([l, mid]\) 和 \([mid + 1, r]\),将两边分别求积分,再加起来就可以了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const double eps = 1e-6;
double a, b, c, d, L, R;
double f(double x) {
return (c * x + d) / (a * x + b);
}
double simpson(double l, double r) {
return (f(r) + f(l) + 4 * f((l + r) / 2)) * (r - l) / 6;
}
double getans(double l, double r) {
double mid = (l + r) / 2;
if(fabs(r - l) <= eps)
return simpson(l, r);
else
return getans(l, mid) + getans(mid, r);
}
int main(){
scanf("%lf%lf%lf%lf%lf%lf", &a, &b, &c, &d, &L, &R);
printf("%.6lf", getans(L, R));
return 0;
}
我觉得这道题目是难在判断收敛性上,而不是代码上。
无穷界积分的审敛法
无穷间断点的审敛法
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const double eps = 1e-8;
double a, L, R;
double f(double x) {
return pow(x, a / x - x);
}
double simpson(double l, double r) {
return (f(r) + f(l) + 4 * f((l + r) / 2)) * (r - l) / 6;
}
double getans(double l, double r, double ans) {
double mid = (l + r) / 2, lans = simpson(l, mid), rans = simpson(mid, r);
if(fabs(lans + rans - ans) <= eps)
return ans;
else
return getans(l, mid, lans) + getans(mid, r, rans);
}
int main(){
scanf("%lf", &a);
L = eps, R = 20;
if(a < 0)
printf("orz");
else
printf("%.5lf", getans(L, R, simpson(L, R)));
return 0;
}
凸包
我觉得这应该算是计算几何中最重要的一个知识点了,不光对于计算几何很重要,对于 DP 也非常重要。
定义
满足能围住平面上一些点的最小凸多边形。
凸多边形就是内角都小于 \(180^{\circ}\)。
\(\text{Andrew}\) 算法
感觉和用单调栈维护决策单调性差不多
首先把所有点以横坐标为第一关键字,纵坐标为第二关键字排序。显然,此时纵坐标最大和最小的点都应该出现在凸包上。
我们只考虑如何求出上凸壳,下凸壳同理。由于上凸壳中每个线段的斜率是单调递减的,于是我们用一个栈来维护凸壳上的点,每次新加入一个点 \(P\),如果 \(P\) 与栈顶点连线的斜率大于栈顶点与次栈顶点联线的斜率,那么我们就将栈顶弹出,直到满足条件或者栈内只有一个点。
洛谷 P2742 [USACO5.1] 圈奶牛Fencing the Cows /【模板】二维凸包
点击查看代码
int n, sta[N], top;
void Convex_hull(){
sort(p + 1, p + n + 1);
for(int i = 1; i <= n; i++){
while(top >= 2 && sgn(Cross(p[sta[top]] - p[sta[top - 1]], p[i] - p[sta[top]])) <= 0)
top--;
sta[++top] = i;
}
int tmp = top;
for(int i = n - 1; i >= 1; i--){
while(top > tmp && sgn(Cross(p[sta[top]] - p[sta[top - 1]], p[i] - p[sta[top]])) <= 0)
top--;
sta[++top] = i;
}
if(n > 1)
top--;
}
\(\text{Graham}\) 扫描法
另外一种求凸包的方法,不需要求两次。
我们先按照所有点的纵坐标排序,那么纵坐标最小的那个点 \(P\) 一定在凸包上。
我们考虑在凸包上逆时针走,那么我们一定是不断地在左拐,也就是说,对于凸包上任意 \(3\) 个连续的点 \(P_1, P_2, P_3\),都有 \(\overrightarrow{P_1 P_2} \times \overrightarrow{P_2 P_3} \geq 0\)。因此我们可以仿照 \(\text{Andrew}\) 算法的流程,拿一个栈来维护当前凸包上的点,然后按照当前点与 \(P\) 的极角大小从小到大尝试将每一个点加入凸包。如果新加入的点让凸包右拐了,那么我们就将栈顶弹出,直到满足条件或者栈内只有一个点。
洛谷 P2742 [USACO5.1] 圈奶牛Fencing the Cows /【模板】二维凸包
点击查看代码
int n, sta[N], top;
void Convex_hull(){
for(int i = 2; i <= n; i++)
if(sgn(p[i].y - p[1].y) < 0 || (sgn(p[i].y - p[1].y) == 0 && sgn(p[i].x - p[1].x) < 0))
swap(p[1], p[i]);
for(int i = 2; i <= n; i++)
p[i].ang = atan2(p[i].y - p[1].y, p[i].x - p[1].x);
sort(p + 2, p + n + 1, cmp);
sta[++top] = 1;
for(int i = 2; i <= n; i++){
while(top >= 2 && sgn(Cross(p[sta[top]] - p[sta[top - 1]], p[i] - p[sta[top]])) < 0)
top--;
sta[++top] = i;
}
}
闵可夫斯基和
闵可夫斯基和在信息学中主要用来合并两个凸包。
对于点集 \(A\) 和 \(B\),定义它们的闵可夫斯基和 \(A + B = \{(X_A + X_B, Y_A + Y_B) | (X_A, Y_A) \in A, (X_B, Y_B) \in B\}\),相当于 \(\boldsymbol x + \boldsymbol y\)。
现在告诉你点集 \(A\) 的和点集 \(B\),需要求出点集 \(A + B\) 的凸包。
首先,新凸包上的点一定是原来的两个凸包上的点加出来的,因为原来不在凸包上的点在新图中也会被包进去,因此我们只用考虑 \(A\) 和 \(B\) 凸包上的点。
在这里,闵可夫斯基和有一个重要的性质,那就是如果点集 \(A\) 和点集 \(B\) 是凸集,那么 \(A + B\) 也是凸集。此时我们需要证明对于两个点 \(e, f \in A + B\),\(e, f\) 之间的线段上的每个点都在 \(A + B\) 内。
于是我们设 \(e = a + c, f = b + d\),\(a, b \in A\),\(c, d \in B\)。根据平面向量的知识,我们知道 \(e, f\) 之间线段上的点可以表示成 \(te + (1 - t)f\),\(t \in [0, 1]\),推下式子,可以得到 \(te + (1 - t)f = t(a + c) + (1 - t)(b + d) = ta + (1 - t)b + [tc + (1 - t)d]\),此时我们发现 \(ta + (1 - t)b\) 在 \(A\) 中,而 \(tc + (1 - t)d\) 在 \(B\) 中,因此 \(te + (1 - t)f\) 一定在 \(A + B\) 中,证明成立。
现在我们已经知道了 \(A + B\) 可以形成一个新的凸包,但是这个凸包的边和点我们还不知道,因此求不出周长与面积这些信息,因此我们还要确定这个凸包的点和边的信息。这里,闵可夫斯基和还有一个重要的性质,那就是如果点集 \(A\) 和点集 \(B\) 是凸集,那么 \(A + B\) 的边集是由凸集 \(A, B\) 的边集按极角排序后连接的结果。
现在我们来证明这个性质。首先我们旋转坐标轴使得凸集 \(A\) 或 \(B\) 中的一条边 \(XY\) 平行于 \(x\) 轴,假设是 \(A\)。再假设凸集 \(A\) 中所有边和凸集 \(B\) 中所有边的斜率都不一样,这样 \(B\) 中就只会有一个最低点 \(U\)。
考虑到闵可夫斯基和相当于向量加法,因此 \(A + B\) 中最低且最靠左的点 \(P\) 一定是由当前 \(A\) 中最低且最靠左的点加上 \(B\) 中最低且最靠左的点得到的,因此 \(\overrightarrow{OP} = \overrightarrow{OX} + \overrightarrow{OU}\)。同理,\(A + B\) 中最低且最靠右的点 \(Q\) 满足 \(\overrightarrow{OQ} = \overrightarrow{OY} + \overrightarrow{OU}\)。
此时 \(A + B\) 中最低的边就是 \(\overrightarrow{PQ} = \overrightarrow{OQ} - \overrightarrow{OP} = \overrightarrow{OY} + \overrightarrow{OU} - \overrightarrow{OX} - \overrightarrow{OU} = \overrightarrow{XY}\),此时我们发现 \(A + B\) 中的每一条边都是由 \(A\) 和 \(B\) 中每一条边平移而来,而我们不断旋转坐标系,相当于是将凸集 \(A, B\) 的边集按极角排序,这就证明了这个性质。
于是我们将 \(A\) 集合中的每条边 \(i\) 和 \(B\) 集合中的每条边 \(j\) 都用向量表示出来,再按照归并排序的思路将两个集合中的边 按极角合并起来。这里有一个小技巧,那就是我们不需要真正的求出极角,而只需要判断 \(\boldsymbol i \times \boldsymbol j\) 的符号即可。如果 \(\boldsymbol i \times \boldsymbol j \geq 0\),那么 \(\boldsymbol i\) 就在 \(\boldsymbol j\) 的顺时针方向,此时 \(\boldsymbol i\) 的极角就比 \(\boldsymbol j\) 小,否则 \(\boldsymbol j\) 的极角就更小。
最后,我们再沿着每条边,求出每个点的坐标。注意此时点的坐标是无序的,还需要再做一遍求凸包的算法才能得到这个凸包。
点击查看代码
vector <Point> Minkowski(vector <Point> &a, vector <Point> &b){
int n = a.size(), m = b.size();
vector <Point> c, tmp1, tmp2;
c.resize(n + m + 1);
c[0] = a[0] + b[0];
tmp1.resize(n + 1);
tmp2.resize(m + 1);
for(int i = 1; i < n; i++)
tmp1[i] = a[i] - a[i - 1];
tmp1[n] = a[0] - a[n - 1];
for(int i = 1; i < m; i++)
tmp2[i] = b[i] - b[i - 1];
tmp2[m] = b[0] - b[m - 1];
int i = 1, j = 1, k = 0;
while(i <= n && j <= m){
if(sgn(Cross(tmp1[i], tmp2[j])) >= 0)
c[++k] = tmp1[i++];
else
c[++k] = tmp2[j++];
}
while(i <= n)
c[++k] = tmp1[i++];
while(j <= m)
c[++k] = tmp2[j++];
for(int i = 1; i <= k; i++)
c[i] = c[i] + c[i - 1];
return c;
}
动态凸包
动态加点
点击查看代码
动态删点
点击查看代码
凸包在 DP 优化中的作用
经典例题
洛谷 P3829 [SHOI2012] 信用卡凸包
点击查看代码
洛谷 P4557 [JSOI2018] 战争
点击查看代码
旋转卡壳
这是一种求解凸包信息时常用的算法,通过名字就可以看出,它相当于是那两个尺子将凸包卡住,再不断的旋转来解决问题。
求凸包直径
洛谷 P1452 【模板】旋转卡壳 | [USACO03FALL] Beauty Contest G
首先,我们通过任意一种求凸包的算法将凸包求出。
接着,我们逆时针枚举每条边,找到离这条直线最远的点 \(x\),然后取这条直线两个端点中离 \(x\) 更远的那个点来更新答案。注意到我们逆时针枚举每条边时,\(x\) 也会逆时针旋转,因此可以直接双指针。
具体的,如果我们求出了距离第 \(i\) 条直线最远的点 \(j\),我们要求出距离第 \(i + 1\) 条直线最远的点,此时我们就判断一下 \(j\) 与第 \(i\) 条直线形成的三角形和 \(j + 1\) 与第 \(i\) 条直线形成的三角形大小,如果后者大就继续比较即可。
注意,我们需要在栈顶再次加入 \(1\) 号节点,使得可以计算 \(1\) 到 \(n\) 这条边。
点击查看代码
void get_diameter(){
if(top < 4) {
ans = sqrdis(p[sta[1]], p[sta[2]]);
return;
}
for(int i = 1, j = 3; i < top; i++){
while(area(sta[i], sta[i + 1], sta[j]) <= area(sta[i], sta[i + 1], sta[j % top + 1]))
j = j % top + 1;
ans = max(ans, max(sqrdis(p[sta[i + 1]], p[sta[j]]), sqrdis(p[sta[i]], p[sta[j]])));
}
}
最小矩形覆盖
点击查看代码
半平面交
点击查看代码
int n, m, cnt, st = 1, ed = 0;
vector <Line> l, l2, q;
vector <Point> p;
void Half_Plain_Intersection(){
int n = l.size();
sort(l.begin(), l.end());
l2.push_back(l[0]);
for(int i = 1; i < n; i++)
if(sgn(ang(l[i].t - l[i].s) - ang(l[i - 1].t - l[i - 1].s)) != 0)
l2.push_back(l[i]);
n = l2.size();
q.resize(n + 10);
for(int i = 0; i < n; i++){
while(st + 1 <= ed && !lft(Intersection(q[ed], q[ed - 1]), l2[i]))
ed--;
while(st + 1 <= ed && !lft(Intersection(q[st], q[st + 1]), l2[i]))
st++;
q[++ed] = l2[i];
}
while(st + 1 <= ed && !lft(Intersection(q[ed], q[ed - 1]), q[st]))
ed--;
q[++ed] = q[st];
p.clear();
for(int i = st; i < ed; i++)
p.push_back(Intersection(q[i], q[i + 1]));
}
平面最近点对
圆相关问题
随机增量法
圆反演
参考资料
-
宋 wc 的课件;
-
计算几何 OI Wiki
-
题解 P4525 【【模板】自适应辛普森法1】 Smallbasic
-
[模板]自适应辛普森法 xcxcli
本文来自博客园,作者:Orange_new,转载请注明原文链接:https://www.cnblogs.com/JPGOJCZX/p/19044653


 浙公网安备 33010602011771号
浙公网安备 33010602011771号