线段树进阶应用学习笔记（三）：扫描线算法相关

空间基本概念

  • \(B\) 维正交范围：在一个 \(B\) 维直角坐标系下，第 \(i\) 维坐标在一个整数范围 \([li,ri]\) 间，内部的点集。

    一般 \(1\) 维正交范围简称区间，\(2\) 维正交范围简称矩形，\(3\) 维正交范围简称长方体。

  • \(\text{2B - Side}\) 的 \(B\) 维正交范围：对于 \(B\) 维正交范围，每一维都有两个限制，即有两条边（\(\text{Side}\)），这样是一个 \(\text{2B - Side}\) 的 \(B\) 维正交范围。

  • \(\text{A - Side}\) 的 \(B\) 维正交范围：对于 \(B\) 维正交范围，如果部分维只有一个限制，则是一个 \(\text{A - Side}\) 的 \(B\) 维正交范围。

    如果有一维没有限制，则这一维是平凡的，没有任何意义，可以简化到一个 \((B - 1)\) 维的问题，这也是扫描线算法的精髓所在。

矩形基本概念

朴素扫描线算法

朴素的扫描线算法和计算几何的关系比较大。

矩阵面积并

矩阵周长并

广义扫描线算法

在朴素的扫描线算法中，我们可以总结出以下思路：\(x\) 轴上一根扫描线从左往右扫，在数据结构上维护当前扫描线上的信息，或者扫过的所有面积中的信息，以此来处理询问，下面我们通过一个扫描线的经典应用来更深入理解扫描线

二维数点

洛谷 P10814 【模板】离线二维数点

扫描线技巧

区间化点技巧

考虑一个区间 \([l, r]\)，其实我们可以将其看成一个二维平面中的点 \((l, r)\)，对于 \([l, r]\) 的限制可以看成若干矩形，进而转化为一个数点的问题，可以用数据结构来维护。

UOJ637 【美团杯2021】A. 数据结构

考虑容斥。我们现在要求全局颜色数，相当于是总颜色数，减掉没有出现的颜色数。

我们考虑，对于一个数字 \(a\)，什么样的操作可以使这个序列中不存在 \(a\)。如果原序列中有 \(a\)，那么我们需要将这些 \(a\) 全部变成 \(a + 1\)。假设 \(a\) 出现的第一个位置是 \(b_a\)，最后一个位置是 \(e_a\)，那么首先一定要满足 \(l \leq b_a \leq e_a \leq r\)。但是，如果这个区间中包含了 \(a - 1\)，那么我们会把它加成 \(1\)，这是不可以的。因此，如果 \([b_a], e_a\) 中有 \(a - 1\)，那么 \(a\) 一定会造成贡献。否则假设 \(b_a\) 之前第一个 \(a - 1\) 出现的位置是 \(p_1\)，\(e_a\) 之后第一个 \(a - 1\) 出现的位置是 \(p_2\)，那么 \(l, r\) 就需要满足 \(p_1 + 1 \leq l \leq b_a\)，\(e_a \leq r \leq p_2 - 1\)。画到平面上就是这样一个矩形：

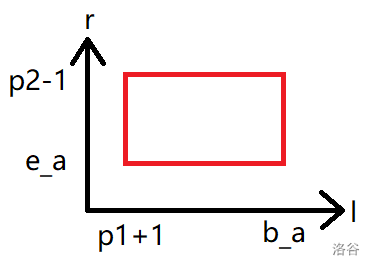
如果原序列中没有 \(a\)，那么我们需要保证 \([l, r]\) 不包含任意一个 \(a - 1\)，因此 \(l, r\) 的范围就锁定在了两个相邻的 \(a - 1\) 之间，画在平面上就是这样一些矩形：

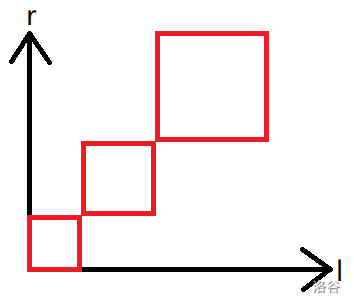
于是现在每个数字就处理好了。对于一个操作 \([l, r]\)，由于对于一个数字 \(a\)，让它不造成贡献的矩形都是不交的，因此我们只需要找到它被多少个矩形包含就可以了，这可以通过简单二维数点完成。

点击查看代码

矩阵信息反演

区间子区间问题

我们之前求解的问题要么是点被多少个矩形包含，或者是矩形包含了多少个点，就不能只讨论矩形吗？有的，兄弟有的，而且这种问题有一个看起来非常难的代表：区间子区间问题。

区间子区间问题一般为以下形式：给一个序列，每次查询区间有多少子区间满足某个条件。

我们这次换一种区间化点的方法。我们将坐标轴两维都设置成序列维，那么一个区间的子区间就可以表示成以下这个矩形：

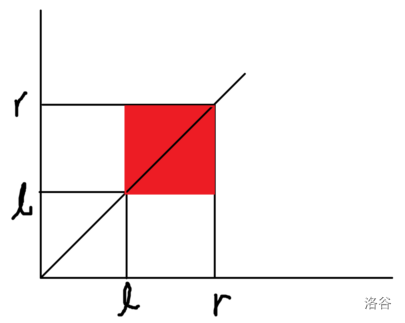
（其实子区间 \([l', r']\) 需要满足 \(r' \geq l'\)，也就是图中斜线上半部分的区域，但是 \(r' \leq l'\) 时，它产生的贡献一定为 \(0\)，因此我们可以将其补成一个完整的矩形）。

我们将这个 \(\text{4 - Side}\) 矩形差分成两个 \(\text{3 - Side}\) 矩形，再拿扫描线扫 \(x\) 这一维，相当于是固定了子区间的右端点，查找有多少个左端点满足条件。由于小于等于 \(r\) 的所有子区间右端点，我们都需要加到答案中，于是现在扫描线上的数据结构就不能光维护当前扫到的信息，而是要维护所有扫过面积的信息，因此我们需要维护历史信息。

一个最简单的例子就是给你平面上若干个矩形，并询问一个 \(\text{2 - Side}\) 矩形所包括的面积。这相当于我们需要快速将一段区间加上某个数，或者询问一段区间的历史和，这里可以查看我的另一篇博客：线段树进阶应用学习笔记（一）：特殊的线段树。

时间-序列问题

这类问题一般是带修改的，而且是一边修改一边询问。似乎扫描线处理不了这种动态的问题，此时我们就需要用到另一种扫描线的方法了。

此时我们不能再将区间分到两个维度了，因此我们将序列看成一维，时间看成一维。如果这个时候扫描时间这一维，维护目前序列的形态不方便，那么我们可以扫描序列这一维，用数据结构维护序列上这一个位置在不同时刻的状态，这样做往往比较简单。

洛谷 P7560 [JOISC 2021] フードコート (Day1)

这道题就是一道经典的时间-序列问题。我们将序列看成一维，时间看成一维，那么一次修改就相当于这样一个 \(\text{3 - Side}\) 矩形：

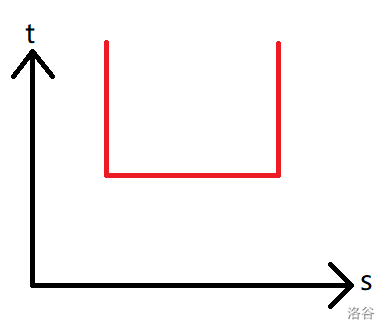
而查询相当于一条竖线，我们要依次执行与这条竖线有交的横线的操作，因此此时的平面长这个样子：

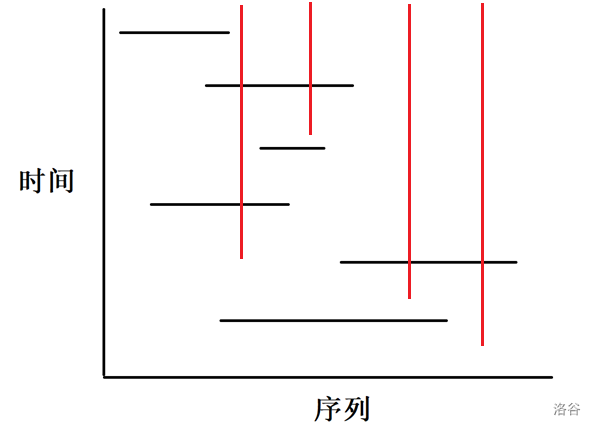
我们一般的思路是扫描时间维，也就是操作序列，维护序列维。但这是我们交换一下，我们扫描序列维

参考资料

posted @ 2025-02-13 19:20  Orange_new  阅读(66)  评论(0)    收藏  举报