线段树进阶应用学习笔记（一）：特殊的线段树

李超线段树

算法流程

洛谷 P4097 【模板】李超线段树 / [HEOI2013] Segment

有一类问题，特别是斜率优化 DP 时，平面上有若干线段，我们需要处理与直线 \(x = x_0\) 相交的线段中，交点纵坐标的最大值，或是该线段的编号，由于线段是有端点的，相当于在某个区间内插入一条直线，这很容易让人想到线段树，我们只需要在线段树的每个区间维护中点处使纵坐标达到最大值的线段编号即可。

但是这用普通线段树很难维护，毕竟两个子区间的维护的线段都可能不是大区间要维护的线段，比如：

复杂度分析

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 9, MOD1 = 39989, MOD2 = 1e9;
const double eps = 1e-9;
struct Line{
    double k, b;
} l[N];
struct Comp{
	double res;
	int id;
};
int s[N << 1], lcnt;
int cmp(double x, double y){
    if(x - y > eps)
        return 1;
    else if(y - x > eps)
        return -1;
    else
        return 0;
}
double calc(int id, int x){
    return l[id].b + x * l[id].k;
}
void modify(int id, int L, int R, int u){
    int &v = s[id], mid = (L + R) >> 1;
    int flag = cmp(calc(u, mid), calc(v, mid));
    if(flag == 1 || (!flag && u < v))
        swap(u, v);
    int flagl = cmp(calc(u, L), calc(v, L)), flagr = cmp(calc(u, R), calc(v, R));
    if(flagl == 1 || (!flagl && u < v))
        modify(id << 1, L, mid, u);
    if(flagr == 1 || (!flagr && u < v))
        modify(id << 1 | 1, mid + 1, R, u);
}
void update(int id, int L, int R, int qL, int qR, int u){
    if(L == qL && R == qR){
        modify(id, L, R, u);
        return;
    }
    int mid = (L + R) >> 1;
    if(qR <= mid)
        update(id << 1, L, mid, qL, qR, u);
    else if(qL > mid)
        update(id << 1 | 1, mid + 1, R, qL, qR, u);
    else {
        update(id << 1, L, mid, qL, mid, u);
        update(id << 1 | 1, mid + 1, R, mid + 1, qR, u);
    }
}
Comp pmax(Comp x, Comp y) {
  if(cmp(x.res, y.res) == -1)
    return y;
  else if(cmp(x.res, y.res) == 1)
    return x;
  else
    return x.id < y.id ? x : y;
}

Comp query(int id, int L, int R, int k){
	if(R < k || k < L)
		return Comp{0, 0};
	int mid = (L + R) >> 1;
	double res = calc(s[id], k);
	if(L == R)
		return Comp{res, s[id]};
	return pmax(Comp{res, s[id]}, pmax(query(id << 1, L, mid, k), query(id << 1 | 1, mid + 1, R, k)));
}
int n, lastans;
int main(){
	scanf("%d", &n);
    while(n--){
        int op, k, x0, y0, x1, y1;
        scanf("%d", &op);
        if(op == 0){
            scanf("%d", &k);
            k = (k + lastans - 1 + MOD1) % MOD1 + 1;
            printf("%d\n", lastans = query(1, 1, MOD1, k).id);
        } else {
            scanf("%d%d%d%d", &x0, &y0, &x1, &y1);
            x0 = (x0 + lastans - 1 + MOD1) % MOD1 + 1;
            x1 = (x1 + lastans - 1 + MOD1) % MOD1 + 1;
            y0 = (y0 + lastans - 1 + MOD2) % MOD2 + 1;
            y1 = (y1 + lastans - 1 + MOD2) % MOD2 + 1;
            if(x0 > x1){
                swap(x0, x1);
                swap(y0, y1);
            }
            lcnt++;
		    if(x0 == x1){
		        l[lcnt].k = 0;
		        l[lcnt].b = max(y0, y1);
		    } else {
		        l[lcnt].k = (y1 - y0) * 1.0 / (x1 - x0);
		        l[lcnt].b = y0 - l[lcnt].k * x0;
		    }
            update(1, 1, MOD1, x0, x1, lcnt);
        }
    }
	return 0;
}

zkw 线段树

吉司机线段树

按理说这不是一个全新形态的线段树，只是一个可以支持新的区间操作，维护新的区间信息的线段树。具体来说，吉司机线段树可以用来解决区间最值操作和区间历史最值查询。

区间最值问题

区间最值操作指，对于一个序列 \(A = (a_i)\)，每次操作我们给出 \((l, r, x)\)，对于所有所有 \(i \in [l, r]\)，将 \(a_i\) 变成 \(\max(a_i, x)\) 或 \(\min(a_i, x)\)。下面我们来看一道最简单的例题。

HDU5306 Gorgeous Sequence

我们发现此时无法使用 Lazy_tag 来快速更新区间答案，因为该区间中有些数要变小，有些数不会有变化，我们无法快速维护。

让我们回到最原本的暴力上来。首先，如果 \(x\) 已经大于等于 \([l, r]\) 的最大值 \(ma\) 了，那么该操作对整个区间没有影响。但是仅特判掉这种情况，感觉复杂度还是会炸。

这时，发动人类智慧，我们再记录一个区间严格次大值 \(se\)，如果 \(se < x < ma\)，那么此时该修改只会对该区间的最大值造成影响，于是我们直接将区间和 \(sum\) 减掉 \(cnt \times (x - ma)\)（\(cnt\) 为区间最大值个数），将 \(ma\) 改成 \(x\)，在该节点打上标记就退出了。

否则我们直接暴力往当前节点的两个儿子进行递归处理。

怎么感觉没有什么优化，之前单侧递归还能接受，这个这么暴力的做法怎么能过？但是，它过了，而且跑得飞快。我们现在就来证明它的复杂度。

首先，我们对线段树进行简化。如果一个节点的最大值等于它父亲节点的最大值，那么我们就将它的最大值删去。由于一个节点的最大值是从两个儿子合并上来得到的，因此一定会有一个儿子的最大值和它父亲的最大值相同。那么除掉这些相同的最大值后，整棵线段树只剩 \(n\) 个节点有最大值了。此时一个节点的最大值比它子树内任意一个最大值都大，且一个没有最大值的点，它实际的最大值为该节点不断向上跳父亲，跳到的第一个有值的节点的最大值。大致的转化如下：

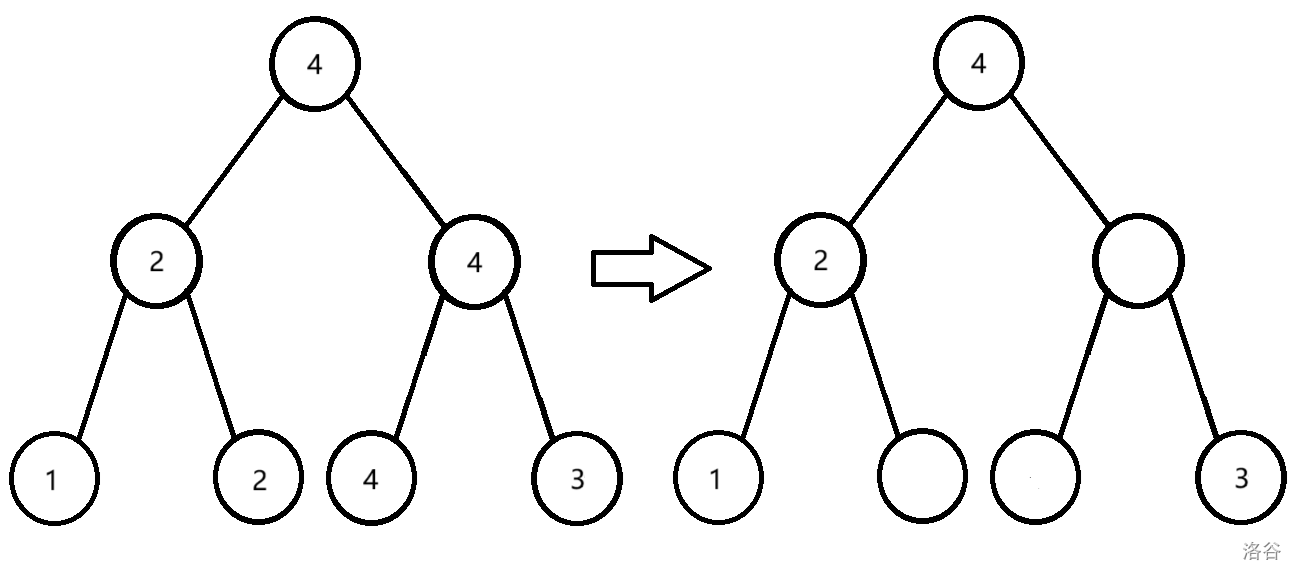
此时我们发现，我们维护的区间严格次大值，就是该区间子树内最大值的最大值，而一次暴力 DFS，相当于在该区间子树内将大于 \(x\) 的最大值全部删除，当所有最大值全部删除完以后，剩下的操作就只会对线段树根进行修改了。于是我们现在要证明的是删除最大值的复杂度。

我们现在来定义一个标记类：

一次区间取 \(\min\) 对节点打上的标记为同一类；
一个标记下传产生的新标记为同一类；
不满足前两种条件的任意两个标记不是同一个标记类。

我们定义一个标记类的权值为拥有这一类标记的节点加上线段树的根节点，在线段树上形成的虚树的大小。我们再定义势能函数 \(\Phi(x)\) 为线段树中所有标记类的权值总和。

考虑一次区间取 \(\min\) 操作，这相当于将标记打到了 \(\mathcal O(\log n)\) 个节点上，会使 \(\Phi(x)\) 至多增加 \(\mathcal O(\log n)\)，而一次标记下传操作只会使 \(\Phi(x)\) 增加 \(\mathcal O(1)\)。

我们考虑 DFS 的过程

区间历史最值

参考资料

黄 jy 的课件
国家集训队2016论文集第 \(6\) 篇吉如一

posted @ 2024-09-20 16:53 Orange_new 阅读(72) 评论(0) 收藏举报

刷新页面返回顶部

JPGOJCZX