组合数学学习笔记(四):特殊的数
前置知识
由于多项式实在是太达芬了,因此所有代码中都不放多项式模板代码部分
卡塔兰数(\(\text{Catalan}\))
斯特林数(\(\text{Stirling}\))
斯特林数作为组合数学中非常重要的一类数,一共分为第一类斯特林数与第二类斯特林数,在处理复杂的小球与盒子的关系时有重要的作用。我们先从比较简单的第二类斯特林数讲起。
第二类斯特林数
定义
记 \(\displaystyle{n \brace k}\) 表示将 \(n\) 个元素划分成 \(k\) 个非空子集的方案数,\(\displaystyle{n \brace k}\) 就叫做第二类斯特林数。
\(n\) 较小时的第二类斯特林数如下:
第二类斯特林数有一些特殊值:
-
\(\displaystyle{n \brace 0} = [n = 0]\):将非零个元素划分为 \(0\) 个集合不存在,将 \(0\) 个元素划分为 \(0\) 个集合算一种情况;
-
\(\displaystyle{n \brace 1} = \displaystyle{n \brace n} = 1\),将 \(n\) 个元素划分为 \(1\) 个集合,每个元素只能放入这一个集合中;将 \(n\) 个元素划分为 \(n\) 个集合,每个元素只能单独成一个集合;
-
\(\displaystyle{n \brace 2} = 2^{n - 1} - 1\),考虑先将 \(1\) 划分到一个集合,再考虑其它 \(n - 1\) 个数是放在有 \(1\) 的这个集合,还是没 \(1\) 的这个集合,最后减去全放在有 \(1\) 的这个集合中的 \(1\) 种情况;
-
\(\displaystyle{n \brace n - 1} = \binom n2\),考虑到此时只有 \(1\) 个集合大小为 \(2\),枚举一下是哪个集合即可。
递推公式与通项公式
递推公式
\(\displaystyle{n \brace k} = k{n - 1 \brace k} + {n - 1 \brace k - 1}\)
即考虑第 \(n\) 个元素放在哪个集合。要么在已经有的 \(k\) 个非空集合里选一个放进去,要么自己单开一个新的集合。
通项公式
\(\displaystyle{n \brace k} = \frac{1}{k!}\sum_{i = 0}^k (-1)^i \binom ki (k - i)^n = \sum_{i = 0}^k \frac{(-1)^{k - i} i^n}{i! (k - i)!}\)
证明:设将 \(n\) 个有标号物品放到 \(i\) 个有标号盒子(允许为空)的方案数为 \(G_i\);将 \(n\) 个有标号物品放到 \(i\) 个有标号盒子(不允许为空)的方案数为 \(F_i\)。
对于 \(G_i\) 的求解是简单的,考虑每个物品放入的是哪个盒子,因此 \(G_i = i^n\)。考虑钦定哪几个盒子非空,于是有 \(G_i = \displaystyle\sum_{j = 0}^i \binom ij F_j\)。
二项式反演一下,可以得到 \(F_i = \displaystyle\sum_{j = 0}^i (-1)^{i - j} \binom ij G_i\),因此 \(F_k = \displaystyle\sum_{i = 0}^k (-1)^{k - i} \binom ki i^n = \sum_{i = 0}^k \frac{k!(-1)^{k - i} i^n}{i! (k - i)!}\)。
由于 \(F_k\) 是有标号的盒子,而 \(\displaystyle{n \brace k}\) 是无标号的盒子,因此将式子再除以 \(k!\) 得到 \(\displaystyle{n \brace k} = \sum_{i = 0}^k \frac{(-1)^{k - i} i^n}{i! (k - i)!}\)。
生成函数
第二类斯特林数是一个二元函数,因此我们使用二元生成函数。
考虑到小球是有标号的,而盒子是无标号的。因此小球这一维我们使用指数生成函数,盒子这一维我们使用普通生成函数。
首先我们考虑单个盒子,我们往里面放球。由于盒子非空,因此我们能拿的球个数的数列为 \(\{0, 1, 1, 1, \dots\}\),我们可以求出这个数列的指数生成函数为 \(e^x - 1\),也就是单个盒子的生成函数。
现在我们再考虑多个盒子。根据 EGF 的卷积的含义,我们知道在盒子数量为 \(k\) 的情况下,第二类斯特林数的生成函数为 \(\displaystyle\frac{(e^x - 1)^k}{k!}\)(除以 \(k!\) 是因为盒子之间没有区别),这就是第二类斯特林数一列的生成函数。现在我们要求出 \(x^n\) 项的系数,也就是 \(n! [x^n] \displaystyle\frac{(e^x - 1)^k}{k!}\),直接多项式指数函数加多项式快速幂即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e6 + 9, MOD = 167772161;
int rev[N], in[N];
void init(){
in[1] = 1;
for(int i = 2; i < N; i++)
in[i] = (MOD - MOD / i) * in[MOD % i] % MOD;
}
int qpow(int x, int y){
int res = 1;
while(y){
if(y & 1)
res = res * x % MOD;
x = x * x % MOD;
y >>= 1;
}
return res;
}
void NTT(int *f, int n, int opt);
int tmp[N << 1];
void inv(int *f, int *g, int n);
int f2[N << 1];
void ln(int *f, int *g, int n);
int lng[N << 1];
void exp(int *f, int *g, int n);
int g[N << 1], res[N << 1];
void qpow(int *f, int n, int k);
int f[N << 1], fac[N], finv[N], n, k;
signed main(){
init();
scanf("%lld%lld", &n, &k);
fac[0] = 1;
for(int i = 1; i <= n; i++)
fac[i] = fac[i - 1] * i % MOD;
finv[n] = qpow(fac[n], MOD - 2);
for(int i = n - 1; i >= 0; i--)
finv[i] = finv[i + 1] * (i + 1) % MOD;
for(int i = 1; i <= n; i++)
f[i] = finv[i];
if(f[0] == 0 && k > n){
for(int i = 0; i <= n; i++)
printf("0 ");
return 0;
}
qpow(f, n, k);
for(int i = 0; i <= n; i++)
printf("%lld ", res[i] * finv[k] % MOD * fac[i] % MOD);
return 0;
}
此时我们再让 \(k\) 这一维成为变量,就可以写出斯特林数最终的生成函数:\(\displaystyle\sum_{j \geq 0} \frac{(e^x - 1)^j}{j!} y^j = \sum_{j \geq 0} \frac{[y(e^x - 1)]^j}{j!} = e^{y(e^x - 1)}\)。
现在我们尝试求出一行的生成函数。我们提取 \(x^n\) 项的系数,注意到我们在指数生成函数中得到的是 \(\displaystyle\frac{x^n}{n!}\) 的系数,因此还需要乘以 \(n!\)。于是:
那么现在,与 \(x^n\) 项的系数有关的只有 \(e^{ix}\) 这一项了,而我们知道 \(e^{ix}\) 的 \(x^n\) 项的系数为 \(\displaystyle\frac{i^n}{n!}\),那么原式中 \(x^n\) 项的系数就是 \(\displaystyle\sum_{j \geq 0} \frac{y^j}{j!} \sum_{i = 0}^j \binom ji i^n (-1)^{j - i} = \sum_{j \geq 0} y^j \sum_{i = 0}^j \frac{i^n}{i!} \frac{(-1)^{j - i}}{(j - i)!}\)。这就是第二类斯特林数一行的生成函数,其中对于每个 \(j\),第二类斯特林数为 \(\displaystyle\sum_{i = 0}^j \frac{i^n}{i!} \frac{(-1)^{j - i}}{(j - i)!}\),这相当于是两个数列 \(\left\{\displaystyle\frac{i^n}{i!} \right\}\) 和 \(\left\{\displaystyle\frac{(-1)^i}{i!} \right\}\) 的卷积,直接多项式科技加速即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e6 + 9, MOD = 167772161;
int rev[N];
int qpow(int x, int y){
int res = 1;
while(y){
if(y & 1)
res = res * x % MOD;
x = x * x % MOD;
y >>= 1;
}
return res;
}
void NTT(int *f, int n, int opt);
int vis[N], prime[N], mi[N], n;
void get_mi(){
mi[0] = 0;
mi[1] = 1;
int cnt = 0;
for(int i = 2; i < N; i++){
if(!vis[i]){
vis[i] = i;
prime[cnt++] = i;
mi[i] = qpow(i, n);
}
for(int j = 0; j < cnt && i * prime[j] < N; j++){
vis[i * prime[j]] = prime[j];
mi[i * prime[j]] = mi[i] * mi[prime[j]] % MOD;
if(i % prime[j] == 0)
break;
}
}
}
int f[N << 1], g[N << 1], fac[N], inv[N];
signed main(){
scanf("%lld", &n);
fac[0] = 1;
for(int i = 1; i <= n; i++)
fac[i] = fac[i - 1] * i % MOD;
inv[n] = qpow(fac[n], MOD - 2);
for(int i = n - 1; i >= 0; i--)
inv[i] = inv[i + 1] * (i + 1) % MOD;
get_mi();
for(int i = 0; i <= n; i++){
f[i] = mi[i] * inv[i] % MOD;
if(i % 2 == 0)
g[i] = inv[i];
else
g[i] = MOD - inv[i];
}
int lim = 1;
while(lim <= 2 * n)
lim <<= 1;
NTT(f, lim, 1);
NTT(g, lim, 1);
for(int i = 0; i <= lim; i++)
f[i] = f[i] * g[i] % MOD;
NTT(f, lim, -1);
for(int i = 0; i <= n; i++)
printf("%lld ", f[i]);
return 0;
}
应用
高阶差分
普通幂转下降幂
\(x^{\underline n}\) 可以写成一个 \(n\) 次的多项式 \(\displaystyle\prod_{i = 0}^{n - 1}(x - i)\),因此 \(x^n\) 一定可以由若干下降幂来表示,计算发现:
可以发现它的系数正好是第二类斯特林数,因此可以得出结论:\(x^n = \displaystyle\sum_{k = 0}^n {n \brace k}x^{\underline k} = \sum_{k = 0}^n {n \brace k} \binom xk k!\)。
证明:
考虑数学归纳法,当 \(n = 0\) 时我们已经证明了这个等式是正确的。现在假设对于 \(0\) 到 \(n - 1\),该等式都成立,现在要证明该等式对于 \(n\) 成立。
首先,我们知道 \(x^{\underline{k + 1}} = x^{\underline k}(x - k)\),于是 \(x \times x^{\underline k} = x^{\underline{k + 1}} + kx^{\underline k}\)。
那么
\(\begin{aligned}x^n &= x \times x^{n - 1} \\&= x \times \displaystyle\sum_{k = 0}^{n - 1} {n - 1 \brace k} x^{\underline k} \\&= \sum_{k = 0}^{n - 1} {n - 1 \brace k} x^{\underline{k + 1}} + \sum_{k = 0}^{n - 1} {n - 1 \brace k} kx^{\underline k} \end{aligned}\)
考虑到 \(\displaystyle{n - 1 \brace 0} 0x^{\underline 0} = {n - 1 \brace n} nx^{\underline n} = 0\),因此可以随意加减在加号右边,因此原式
\(\begin{aligned} \\&= \sum_{k = 1}^n {n - 1 \brace k - 1} x^{\underline k} + \sum_{k = 1}^n {n - 1 \brace k} kx^{\underline k} \\&= \sum_{k = 1}^n ({n - 1 \brace k - 1} + k {n - 1 \brace k}) x^{\underline k} \\&= \sum_{k = 0}^n {n \brace k}x^{\underline k}\end{aligned}\)
即,我们可以将第二类斯特林数看成,由普通幂转为下降幂时,产生的系数。
普通幂转上升幂
类似下降幂来定义上升幂为 \(x^{\overline n} = x(x + 1)(x + 2) \dots (x + n - 1) = \displaystyle\prod_{i = 0}^{n - 1}(x + i)\)。
我们将 \(-x\) 带入 \(\displaystyle\sum_{k = 0}^n {n \brace k}x^{\underline k}\) 得到 \((-1)^n x^n = \displaystyle\sum_{k = 0}^n {n \brace k} (-x)^{\underline k}\),而 \(x^{\underline n} = (-1)^n(-x)^{\overline n}\),于是可以得到 \(x^n = \displaystyle\sum_{k = 0}^n (-1)^{n - k} {n \brace k} x^{\overline k}\)。
第一类斯特林数
定义
记 \(\displaystyle{n \brack k}\) 表示将 \(n\) 个元素划分成 \(k\) 个圆排列的方案数,\(\displaystyle{n \brack k}\) 就叫做第一类斯特林数。
圆排列是指将一个排列围成一个圈,如果两个圆排列旋转之后一样,那么这两个圆排列就是相同的,比如 \([A, B, C, D] = [B, C, D, A] = [C, D, A, B] = [D, A, B, C]\)(\([x_1, x_2, \dots, x_n]\) 表示从竖直方向顺时针依次填入 \(x_1, x_2, \dots, x_n\),最后又回到竖直方向上所形成的圆排列)。
\(n\) 较小时的第一类斯特林数如下:
第一类斯特林数有一些特殊值:
-
\(\displaystyle{n \brack 0} = [n = 0]\):将非零个元素划分为 \(0\) 个圆排列不存在,将 \(0\) 个元素划分为 \(0\) 个圆排列算一种情况;
-
\(\displaystyle{n \brack n} = 1(n > 0)\):将 \(n\) 个元素划分为 \(n\) 个圆排列,每个元素只能单独成一个圆排列;
-
\(\displaystyle{n \brack 1} = (n - 1)!(n > 0)\):考虑到普通排列的数量有 \(n!\) 个,每个圆排列对应 \(n\) 个普通排列,于是圆排列的数量就变成了 \(\displaystyle\frac{n!}{n} = (n - 1)!\);
-
\(\displaystyle{n \brack n - 1} = \binom n2\),考虑到此时只有 \(1\) 个圆排列大小为 \(2\),枚举一下是哪个圆排列即可。
可以发现,在第二类斯特林数分成的 \(k\) 个集合中,第一类斯特林数还要考虑顺序,因此 \(\displaystyle{n \brack k} \geq {n \brace k}\)。
递推公式
\(\displaystyle{n \brack k} = (n - 1){n - 1 \brack k} + {n - 1 \brack k - 1}\)。
即考虑第 \(n\) 个元素是插入这 \(k\) 个圆排列中的哪个位置,也就是考虑是将那个圆排列中的哪条边断掉,将第 \(n\) 个元素插入再接上,可以发现一共有 \(n - 1\) 条边可以断掉再插入,因此一共有 \((n - 1)\displaystyle{n - 1 \brack k}\) 种选择:

\(\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Huge\Downarrow\)

由于第 \(n\) 个元素还能自成一个圆排列,因此 \(\displaystyle{n \brack k} = (n - 1){n - 1 \brack k} + {n - 1 \brack k - 1}\)。
可惜的是,第一类斯特林数没有实用的通项公式 (虽然第二类斯特林数的通项公式也不实用)。
生成函数
仿照第二类斯特林数的推导,我们还是先求一个圆排列的生成函数。我们之前求出了 \(\displaystyle{n \brack 1} = (n - 1)!\),由于一个圆排列非空,且小球有标号,于是一个圆排列的生成函数就是 \(\displaystyle\sum_{i \geq 1} (i - 1)! \frac{x^i}{i!} = \sum_{i \geq 1} \frac{x^i}{i} = -\ln (1 - x)\)。
我们再来考虑 \(k\) 个圆排列,依然利用 EGF 卷积的含义,可以得到此时第一类斯特林数的生成函数为 \(\displaystyle\frac{(-1)^k \ln^k (1 - x)}{k!}\),这就是第一类斯特林数一列的生成函数。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e6 + 9, MOD = 167772161;
int rev[N], in[N];
void init(){
in[1] = 1;
for(int i = 2; i < N; i++)
in[i] = (MOD - MOD / i) * in[MOD % i] % MOD;
}
int qpow(int x, int y){
int res = 1;
while(y){
if(y & 1)
res = res * x % MOD;
x = x * x % MOD;
y >>= 1;
}
return res;
}
void NTT(int *f, int n, int opt);
int f2[N << 1];
void ln(int *f, int *g, int n);
int lng[N << 1];
void exp(int *f, int *g, int n);
int g[N << 1], res[N << 1];
void qpow(int *f, int n, int k);
int f[N << 1], fac[N], finv[N], n, k;
signed main(){
init();
scanf("%lld%lld", &n, &k);
fac[0] = 1;
for(int i = 1; i <= n; i++)
fac[i] = fac[i - 1] * i % MOD;
for(int i = 1; i <= n; i++)
f[i] = in[i];
if(f[0] == 0 && k > n){
for(int i = 0; i <= n; i++)
printf("0 ");
return 0;
}
qpow(f, n, k);
int invk = qpow(fac[k], MOD - 2);
for(int i = 0; i <= n; i++)
printf("%lld ", res[i] * invk % MOD * fac[i] % MOD);
return 0;
}
现在我们再让 \(k\) 这一维成为变量,就可以得到第一类斯特林数的二元生成函数 \(\displaystyle\sum_{j \geq 0}\displaystyle\frac{(-1)^j \ln^j (1 - x)}{j!} y^j = \sum_{j \geq 0} \frac{[-y \ln (1 - x)]^j}{j!} = e^{-y \ln (1 - x)} = \left(e^{\ln (1 - x)} \right)^{-y} = (1 - x)^{-y}\)。
现在我们再来求第一类斯特林数一行的生成函数,也就是 \(n! [x^n] (1 - x)^{-y}\)。用二项式定理展开,可以得到 \(n! [x^n] (1 - x)^{-y} = n! [x^n] \displaystyle\sum_{i = 1}^{-y} \binom{-y}{i} (-x)^i = n! \binom{-y}{n} (-1)^n = (-1)^n (-y)^{\overline n} = y^{\overline n}\)。
不过此时直接计算直接爆炸,注意到 \(y^{\overline{2n}} = y^{\overline n} \times (y + n)^{\overline n}\),而 \((y + n)^{\overline n}\) 可以通过 \(y^{\overline n}\) 平移得来,再将两边乘在一起即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e6 + 9, MOD = 167772161;
int rev[N], fac[N], in[N];
int qpow(int x, int y){
int res = 1;
while(y){
if(y & 1)
res = res * x % MOD;
x = x * x % MOD;
y >>= 1;
}
return res;
}
void NTT(int *f, int n, int opt);
void mul(int *f, int *g, int n, int m);
int tmp1[N << 1], tmp2[N << 1];
void trans(int *f, int c, int n);
void solve(int *f, int n){
if(n == 1)
f[1] = 1;
else if(n & 1){
solve(f, n - 1);
for(int i = n; i >= 1; i--)
f[i] = (f[i - 1] + f[i] * (n - 1) % MOD) % MOD;
f[0] = f[0] * (n - 1) % MOD;
} else {
solve(f, n / 2);
trans(f, n / 2, n / 2);
mul(f, tmp2, n / 2, n / 2);
for(int i = 0; i <= 4 * n; i++)
tmp2[i] = 0;
}
}
int f[N << 1], n;
signed main(){
scanf("%lld", &n);
fac[0] = 1;
for(int i = 1; i <= n; i++)
fac[i] = fac[i - 1] * i % MOD;
in[n] = qpow(fac[n], MOD - 2);
for(int i = n - 1; i >= 0; i--)
in[i] = in[i + 1] * (i + 1) % MOD;
solve(f, n);
for(int i = 0; i <= n; i++)
printf("%lld ", f[i]);
return 0;
}
应用
上升幂转普通幂
\(x^{\overline n}\) 可以写成一个 \(n\) 次的多项式 \(\displaystyle\prod_{i = 0}^{n - 1}(x + i)\),可以发现这也是一个关于 \(x\) 的 \(n\) 次多项式,因此 \(x^{\overline n}\) 一定可以由若干普通幂来表示,计算发现:
可以发现它的系数正好是第一类斯特林数,因此可以得出结论:\(x^{\overline n} = \displaystyle\sum_{k = 0}^n {n \brack k} x^k\)。
证明:
还是考虑数学归纳法,当 \(n = 0\) 时我们已经证明了这个等式是正确的。现在假设对于 \(0\) 到 \(n - 1\),该等式都成立,现在要证明该等式对于 \(n\) 成立。
这次,我们要知道 \((x + n - 1)^k \times x^k = x^{k + 1} + (n - 1)x^k\)。
那么
\(\begin{aligned} x^{\overline n} &= (x + n - 1) x^{\overline{n - 1}} \\&= (x + n - 1) \displaystyle\sum_{k = 0}^{n - 1} {n - 1 \brack k} x^k \\&= \sum_{k = 0}^{n - 1} {n - 1 \brack k} x^{k + 1} + \sum_{k = 0}^{n - 1} (n - 1) {n - 1 \brack k} x^k\end{aligned}\)
一样的道理,\(\displaystyle{n - 1 \brack 0} (n - 1)x^0 = {n - 1 \brack n} (n - 1)x^n = 0\),因此可以随意加减在加号右边,因此原式
\(\begin{aligned} &= \displaystyle\sum_{k = 1}^n {n - 1 \brack k - 1} x^k + \sum_{k = 1}^n (n - 1) {n - 1 \brack k} x^k \\&= \sum_{k = 1}^n [(n - 1) {n - 1 \brack k} + {n - 1 \brack k - 1}] x^k \\&= \sum_{k = 0}^n {n \brack k} x^k\end{aligned}\)
即,我们可以将第一类斯特林数看成,从上升幂转普通幂时,产生的常数。
其实,通过刚才第一类斯特林数一行的生成函数的证明,我们也可以推出这个式子。
下降幂转普通幂
考虑到上升幂和下降幂奇数次方项的系数正好相反:
因为 \(x^{\overline n} = \displaystyle\sum_{k = 0}^n {n \brack k} x^k\),所以 \(x^{\underline n} = \displaystyle\sum_{k = 0}^n (-1)^{n - k} {n \brack k} x^k\)。
反转公式
现在我们已经会了各种幂之间的转化。由于转化一定会用到斯特林数,因此我们可以在第一类和第二类斯特林数之间建立一些关系。
我们将普通幂先转化成上升幂,得到 \(x^n = \displaystyle\sum_{k = 0}^n (-1)^{n - k} {n \brace k} x^{\overline k}\),再将上升幂转化回普通幂,得到 \(x^n = \displaystyle\sum_{k = 0}^n \sum_{m = 0}^k (-1)^{n - k} {n \brace k} {k \brack m} x^m\)。由于等式两边相等,那么只有 \(k = m = n\) 的时候该式才会有值,因此我们可以得到 \(\displaystyle\sum_{k = 0}^n (-1)^{n - k} {n \brace k} {k \brack m} = [m = n]\)。
同样的,我们先将普通米转化成下降幂,再将下降幂转化回普通幂,就可以得到另一个反转公式 \(\displaystyle\sum_{k = 0}^n (-1)^{n - k} {n \brack k} {k \brace m} = [m = n]\)。
这是两个非常重要的斯特林恒等式,在求解一些困难斯特林数问题时很有用。其他的斯特林恒等式就放在后面讲解了。
经典例题
CF932E Team Work
直接暴力推式子即可。
此时就可以在 \(O(k^2)\) 的时间复杂度内解决问题。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int K = 5e3 + 9, MOD = 1e9 + 7;
int s[K][K], n, k, ans;
int qpow(int a, int b){
int res = 1;
while(b > 0){
if(b & 1)
res = 1ll * res * a % MOD;
a = 1ll * a * a % MOD;
b >>= 1;
}
return res;
}
int main(){
scanf("%d%d", &n, &k);
s[0][0] = 1;
for(int i = 1; i <= k; i++)
for(int j = 1; j <= k; j++)
s[i][j] = (1ll * j * s[i - 1][j] + s[i - 1][j - 1]) % MOD;
for(int i = 0, j = 1; i <= k; i++){
ans = (ans + 1ll * s[k][i] * j % MOD * qpow(2, n - i) % MOD) % MOD;
j = 1ll * j * (n - i) % MOD;
}
printf("%d", ans);
return 0;
}
洛谷 P6620 [省选联考 2020 A 卷] 组合数问题
首先把 \(f(x)\) 写成下降幂多项式 \(\displaystyle\sum_{i = 0}^m a_i i^k = \sum_{i = 0}^m a_i \sum_{j = 0}^i {i \brace j} k^{\underline j} = \sum_{i = 0}^m \left(\sum_{j = i}^m {j \brace i} a_j \right) k^{\underline i}\)(交换求和顺序后再将 \(i\) 和 \(j\) 的意义互换),发现内部的 \(\sum_{j = i}^m {j \brace i} a_j\) 是好求的,将其设为 \(b_i\),那么问题变成了求 \(\displaystyle\sum_{k = 0}^n \sum_{i = 0}^m b_i k^{\underline i} \times x^k \times \binom nk\)。
由于 \(\displaystyle\binom nk \times k^{\underline i} = \binom nk \binom ki i! = \binom ni i! \binom{n - i}{k - i} = n^{\underline i} \binom{n - i}{k - i}\),那么原式 \(= \displaystyle\sum_{i = 0}^m b_i n^{\underline i} \sum_{k = 0}^n \binom{n - i}{k - i} x^k = \sum_{i = 0}^m b_i n^{\underline i} x^i \sum_{k = 0}^{n - i} \binom{n - i}{k} x^k\)。
可以发现里面是一个二项式定理的形式,于是原式最终 \(= \displaystyle\sum_{i = 0}^m b_i n^{\underline i} x^i (x + 1)^{n - i}\),于是用 \(O(m^2)\) 的时间复杂度解决了此题。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e3 + 9;
int s[N][N], d[N], a[N], b[N], n, x, p, m;
int qpow(int a, int b){
int res = 1;
while(b > 0){
if(b & 1)
res = res * a % p;
a = a * a % p;
b >>= 1;
}
return res;
}
signed main(){
scanf("%lld%lld%lld%lld", &n, &x, &p, &m);
s[0][0] = 1;
for(int i = 1; i < N; i++)
for(int j = 1; j < N; j++)
s[i][j] = (j * s[i - 1][j] + s[i - 1][j - 1]) % p;
for(int i = 0; i <= m; i++)
scanf("%lld", &a[i]);
for(int i = 0; i <= m; i++)
for(int j = i; j <= m; j++)
b[i] = (b[i] + s[j][i] * a[j]) % p;
d[0] = 1;
for(int i = n, j = 1; i >= (n - m + 1); i--, j++)
d[j] = d[j - 1] * i % p;
int ans = 0;
for(int i = 0; i <= m; i++)
ans = (ans + b[i] * d[i] % p * qpow(x, i) % p * qpow(x + 1, n - i) % p) % p;
printf("%lld", ans);
return 0;
}
洛谷 P4609 [FJOI2016] 建筑师
这个建筑师建造的城市让我想起了 指环王 中的:

考虑把最大值作为分界点,左边的前缀最大值构成一个 \(A - 1\) 个台阶的阶梯,后缀最大值构成了一个 \(B - 1\) 个台阶的阶梯:
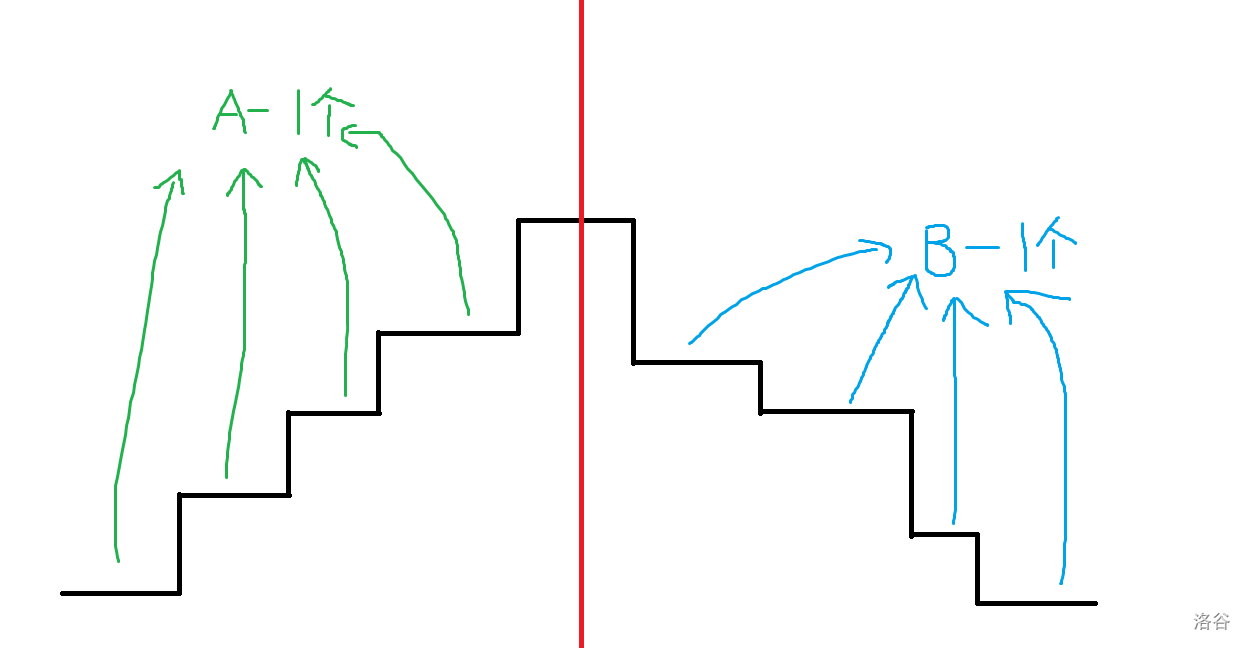
现在每个阶梯分成一个组,每个组内除了最大值必须在第一个,其它值可以随便排,考虑到高度是 \(1\) 到 \(n\) 的排列,于是无论怎么分组,每组都有最大值,将每组最大值排序后,一定可以得到一个如图的阶梯。由于要考虑顺序,因此分组的方案数是 \(\displaystyle{n - 1 \brack A + B - 2}\)。
现在考虑哪些值在左边的阶梯,哪些值在右边的阶梯,因此分左右的组合有 \(\displaystyle\binom{A + B - 2}{A - 1}\) 种,最终答案为 \(\displaystyle{n - 1 \brack A + B - 2} \times \binom{A + B - 2}{A - 1}\),\(O(nm)\) 预处理斯特林数,\(O(m^2)\) 预处理组合数就可以 \(O(T)\) 求出答案了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 5e4 + 9, M = 2e2 + 9, MOD = 1e9 + 7;
int s[N][M], b[M][M], T, n, A, B;
signed main(){
s[0][0] = 1;
for(int i = 1; i < N; i++)
for(int j = 1; j < M; j++)
s[i][j] = ((i - 1) * s[i - 1][j] + s[i - 1][j - 1]) % MOD;
for(int i = 0; i < M; i++)
b[i][0] = 1;
for(int i = 1; i < M; i++)
for(int j = 1; j < M; j++)
b[i][j] = (b[i - 1][j] + b[i - 1][j - 1]) % MOD;
scanf("%lld", &T);
while(T--){
scanf("%lld%lld%lld", &n, &A, &B);
printf("%lld\n", s[n - 1][A + B - 2] * b[A + B - 2][A - 1] % MOD);
}
return 0;
}
洛谷 P4827 [集训队互测 2011] Crash 的文明世界
此题需要一定的转化技巧,不只是单纯推式子。
我们依然运用斯特林数将通常幂转化成下降幂:\(\displaystyle\sum_{v = 1}^n \operatorname{dist} (u, v)^k = \sum_{v = 1}^n \sum_{i = 0}^k {k \brace i} \binom{\operatorname{dist} (u, v)}{i} i! = \sum_{i = 0}^k {k \brace i} i! \sum_{v = 1}^n \binom{\operatorname{dist} (u, v)}{i}\)。
此时我们发现式子已经推不动了,因此我们考虑将其转化成一个 DP 问题。我们设 \(dp_{u, i} = \displaystyle\sum_{v \in \operatorname{subtree} (u)}^n \binom{\operatorname{dist} (u, v)}{i}\),那么 \(\displaystyle\sum_{v \in \operatorname{subtree} (u)}^n \binom{\operatorname{dist} (u, v)}{i} = \sum_{v \in \operatorname{subtree} (u)}^n \binom{\operatorname{dist} (u, v) - 1}{i} + \binom{\operatorname{dist} (u, v) - 1}{i - 1}\)。此时我们注意到 \(\operatorname{dist} (u, v) - 1\) 刚好就等于 \(u\) 的某个儿子 \(s\) 到 \(s\) 子树内的点的距离,因此可以将 DP 函数再次改写成 \(dp_{u, i} = \displaystyle\sum_{v \in \operatorname{son} (u)} dp_{v, i} + dp_{u, i}\)。
此时我们就可以通过换根 DP 求出以每个点为根时的答案,乘上 \(\displaystyle{k \brace i} i!\) 就可以得到这个城市的指标值了。时间复杂度 \(O(nk)\)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 5e4 + 9, K = 1.5e2 + 9, MOD = 1e4 + 7;
struct Edge{
int v, nex;
} e[N << 1];
int head[N], ecnt;
void addEdge(int u, int v){
e[++ecnt] = Edge{v, head[u]};
head[u] = ecnt;
}
int s[K][K], dp[N][K], fac[K], n, k;
void dfs1(int u, int fa){
dp[u][0] = 1;
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(v == fa)
continue;
dfs1(v, u);
for(int j = 1; j <= k; j++)
dp[u][j] = (dp[u][j] + dp[v][j] + dp[v][j - 1]) % MOD;
dp[u][0] = (dp[u][0] + dp[v][0]) % MOD;
}
}
int tmp[K];
void dfs2(int u, int fa){
if(fa){
for(int i = 1; i <= k; i++)
tmp[i] = (dp[fa][i] - (dp[u][i] + dp[u][i - 1]) % MOD + MOD) % MOD;
tmp[0] = (dp[fa][0] - dp[u][0] + MOD) % MOD;
for(int i = 1; i <= k; i++)
dp[u][i] = (dp[u][i] + tmp[i] + tmp[i - 1]) % MOD;
dp[u][0] = (dp[u][0] + tmp[0]) % MOD;
}
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(v == fa)
continue;
dfs2(v, u);
}
}
signed main(){
scanf("%lld%lld", &n, &k);
for(int i = 1; i < n; i++){
int u, v;
scanf("%lld%lld", &u, &v);
addEdge(u, v);
addEdge(v, u);
}
s[0][0] = 1;
for(int i = 1; i <= k; i++)
for(int j = 1; j <= k; j++)
s[i][j] = (j * s[i - 1][j] + s[i - 1][j - 1]) % MOD;
fac[0] = 1;
for(int i = 1; i <= k; i++)
fac[i] = fac[i - 1] * i % MOD;
dfs1(1, 0);
dfs2(1, 0);
for(int i = 1; i <= n; i++){
int ans = 0;
for(int j = 0; j <= k; j++)
ans = (ans + dp[i][j] * s[k][j] % MOD * fac[j] % MOD) % MOD;
printf("%lld\n", ans);
}
return 0;
}
某联考题
给定 \(n, m, b, c\),求满足下列条件的 \(m\) 元组 \((x_1, x_2, x_3, \dots, x_m)\) 的个数模 \(998244353\)。
-
\(x_i \in [0, b^i - c] \cap \mathbb Z\);
-
\(\displaystyle\sum x_i \leq n\)。
\(2 \leq b < 10^8\),\(-10^8 \leq c < b\),\(1 \leq m \leq 80\),\(1 \leq n \leq b^{m + 1}\),\(n\) 用高精度表示。
斯特林数恒等式
斯特林反演
斯特林反演的式子如下:
它还有另一种形式:
证明:这里只证明第 \(1\) 个式子,另外一个式子的推导类似。
我们写出 \(f(n)\) 的指数生成函数(不知道为什么要用指数生成函数,可能是方便计算),然后大力推式子:
我们发现第二层和式就是求斯特林数一列的生成函数,等于 \(\displaystyle\frac{(e^x - 1)^k}{k!}\),现在继续推式子:
此时我们就可以得到 \(G(x) = F(\ln(1 + x))\),此时我们再将 \(F(\ln(1 + x))\) 展开:
我们发现 \(\displaystyle\frac{(-1)^k \ln^k [1 - (-x)]}{k!}\) 就是第一类斯特林数一列的生成函数,于是我们将其展开:
我们又知道 \(G(x) = \displaystyle\sum_{i \geq 0} g_i \frac{x^i}{i!}\),对比两式的系数可以得出 \(g_i = \displaystyle\sum_{k = 0}^i (-1)^{i - k} {k \brack i} f_k\),证明成立。
我们先忽略每一列互不相同的限制,先求出每一行互不相同的情况数。由于每一个格子可以填 \(c\) 种不同的数字,一次一行就有 \(c^m\) 种不同的填法,这 \(n\) 行就有 \((c^m)^{\underline n}\) 种不同的填法。也可以说是,仅考虑行不相同,这 \(m\) 列一共有 \((c^m)^{\underline n}\) 种不同的填法。
我们现在再加入列的限制。我们设 \(f(i)\) 表示这 \(m\) 列一共有 \(i\) 中不同的填法的方案数。
欧拉数(\(\text{Eulerian}\))
调和级数(\(\text{Harmonic}\))
伯努利数(\(\text{Bernoulli}\))
定义
考虑自然数的幂的和 \(S_m(n) = 0^m + 1^m + 2^m + \dots + (n - 1)^m = \displaystyle\sum_{i = 0}^{n - 1} i^m\),我们来观察 \(m\) 取特殊值时该式子的变化:
可以发现系数之间存在一些关系。首先可以发现 \(S_m(n)\) 一定是一个 \(m + 1\) 次多项式,它的 \(n^{m + 1}\) 项的系数一定是 \(\displaystyle\frac{1}{m + 1}\),\(n^m\) 项的系数一定是 \(-\displaystyle\frac 12\),\(n^{m - 1}\) 项的系数一定是 \(\displaystyle\frac{m}{12}\),\(n^{m - 2}\) 项的系数一定是 \(0\),\(n^{m - 3}\) 项的系数一定是 \(\displaystyle\frac{-m(m - 1)(m - 2)}{720}\)……。当 \(n^{m - 3}\) 项的系数出现时,我们可以猜想 \(n^{m - k}\) 项的系数应该是某个常数乘以 \(m^{\underline k}\),于是 \(S_m(n) = \displaystyle\frac{1}{m + 1}\sum_{i = 0}^m \binom{m + 1}{i} B_i n^{m + 1 - i}\),其中的 \(B_i\) 就被称作伯努利数。
伯努利数隐含一个递归关系:\(\displaystyle\sum_{j = 0}^m \binom{m + 1}{j} B_j = [m = 0]\),这会在后续用伯努利数的指数生成函数证明,此处可以先当结论记住。
伯努利数意义
刚才我们猜想 \(S_m(n) = \displaystyle\frac{1}{m + 1}\sum_{i = 0}^m \binom{m + 1}{i} B_i n^{m + 1 - i}\),现在我们来证明它。
考虑数学归纳法。
边界情况是好证的,同时我们也可以证明 \(B_0 = 1\)。
假设对于 \(0\) 到 \(m - 1\),都有 \(S_i(n) = \displaystyle\frac{1}{m + 1}\sum_{i = 0}^m \binom{m + 1}{i} B_i n^{m + 1 - i}\)。
首先,先进行一个简单的变换,那就是 \(S_{m + 1}(n) + n^{m + 1} = \displaystyle\sum_{i = 0}^{n - 1}(i + 1)^{m + 1} = \sum_{i = 0}^{n - 1}\sum_{j = 0}^{m + 1} \binom{m + 1}{j} i^j\)(用下指标一行之和展开)\(= \displaystyle\sum_{j = 0}^{m + 1} \binom{m + 1}{j} S_j(n)\),于是两边同时减去 \(S_{m + 1}(n)\),可以得到 \(n^{m + 1} = \displaystyle\sum_{j = 0}^{m} \binom{m + 1}{j} S_j(n)\)。
现在考虑一个新的求和方法:扰动法。我们先设 \(\hat{S}_m(n) = \displaystyle\frac{1}{m + 1}\sum_{i = 0}^m \binom{m + 1}{i} B_i n^{m + 1 - i}\),于是我们想证明 \(S_m(n) = \hat{S}_m(n)\),现在我们知道这对于 \(0\) 到 \(m - 1\) 成立,假设在 \(m\) 作为指数时 \(S_m(n)\) 与 \(\hat{S}_m(n)\) 有差距 \(\Delta\),现在我们要证明 \(\Delta = 0\)。
由于 \(n^{m + 1} = \displaystyle\sum_{j = 0}^{m} \binom{m + 1}{j} S_j(n)\),将最后一项提出,那么前面所有 \(S_m(n)\) 都 \(= \hat{S}_{m}(n)\),而最后一项与 \(\hat{S}_m(n)\) 与 \(S_m(n)\) 差 \(\Delta\),于是 \(\displaystyle\sum_{j = 0}^{m} \binom{m + 1}{j} S_j(n) = \sum_{j = 0}^{m} \binom{m + 1}{j} \hat{S}_j(n) + \binom{m + 1}{m} \Delta = \sum_{j = 0}^{m} \binom{m + 1}{j} \hat{S}_j(n) + (m + 1) \Delta\)。
将 \(\hat{S}_m(n)\) 展开,于是可以得到原式
考虑改变 \(k\) 的意义,变成 \(j\) 与 \(k\) 的差值,于是原式
发现其中有一个三项式系数恒等,将其变换后再调整求和顺序可以得到原式
再次改变 \(j\) 的意义为 \(j\) 与 \(k\) 的差值,于是原式
可以发现 \(\displaystyle\sum_{j = 0}^{m - k} \binom{m + 1 - k}{j} B_j\) 是伯努利数的递归关系,于是原式
现在我们就知道了 \(n^{m + 1} = n^{m + 1} + (m + 1)\Delta\),于是 \(\Delta = 0\),于是对于 \(m\),也有 \(S_m(n) = \hat{S}_m(n)\),符合数学归纳法,等式成立。
生成函数
分拆数(\(\text{Partition}\))
施罗德数(\(\text{Schroder}\))
参考资料
本文来自博客园,作者:Orange_new,转载请注明原文链接:https://www.cnblogs.com/JPGOJCZX/p/18688631


 浙公网安备 33010602011771号
浙公网安备 33010602011771号