基于主成分分析(PCA)的故障诊断MATLAB仿真
一、核心代码实现
%% PCA故障诊断仿真程序
% 清空环境
clc; clear; close all;
%% 1. 数据加载与预处理
% 加载TEP数据集(需提前下载)
load('d00.dat'); % 正常数据
load('d2_te.dat'); % 测试数据(含故障)
X_train = double(d00'); % 转置适配维度
X_test = double(d2_te');
% 数据标准化
[X_mean, X_std] = deal(mean(X_train,2), std(X_train,0,2));
X_train_norm = (X_train - repmat(X_mean,1,size(X_train,2))) ./ repmat(X_std,1,size(X_train,2));
X_test_norm = (X_test - repmat(X_mean,1,size(X_test,2))) ./ repmat(X_std,1,size(X_test,2));
%% 2. PCA模型构建
% 协方差矩阵计算
SXtrain = cov(X_train_norm');
% 特征值分解
[T,lm] = eig(SXtrain);
[~,idx] = sort(diag(lm),'descend');
T = T(:,idx);
lm = diag(idx);
% 主元选择(累计贡献率>90%)
cumsum_ratio = cumsum(lm)/sum(lm);
num_pc = find(cumsum_ratio >= 0.9, 1);
% 投影矩阵
P = T(:,1:num_pc);
%% 3. 控制限计算
alpha = 0.01; % 置信水平99%
n = size(X_train,2); % 样本维度
% T²控制限
T2_UCL = num_pc*(n-1)*(n+1)/(n*(n-num_pc)) * finv(alpha,num_pc,n-num_pc);
% SPE控制限计算
th = [sum((lm(num_pc+1:end)).^1), sum((lm(num_pc+1:end)).^2), sum((lm(num_pc+1:end)).^3)];
h0 = 1 - 2*th(1)*th(3)/(3*th(2)^2);
ca = norminv(1-alpha);
QU = th(1)*(h0*ca*sqrt(2*th(2))/th(1) + 1 + th(2)*h0*(h0-1)/th(1)^2)^(1/h0);
%% 4. 模型测试
% 标准化测试数据
X_test_proj = (X_test_norm - repmat(X_mean,1,size(X_test,2))) ./ repmat(X_std,1,size(X_test,2));
% 统计量计算
T2 = zeros(size(X_test,2),1);
SPE = zeros(size(X_test,2),1);
for i = 1:size(X_test,2)
x = X_test_proj(:,i);
T2(i) = x'*P'*inv(lm(1:num_pc,1:num_pc))*P*x;
SPE(i) = x'*(eye(n) - P*P')*x;
end
%% 5. 结果可视化
figure;
subplot(2,1,1);
plot(1:length(T2),T2,'b',1:length(T2),T2_UCL*ones(size(T2)),'r--');
title('T²控制图'); xlabel('样本序号'); ylabel('T²值');
legend('T²统计量','控制限');
subplot(2,1,2);
plot(1:length(SPE),SPE,'g',1:length(SPE),QU*ones(size(SPE)),'m--');
title('SPE控制图'); xlabel('样本序号'); ylabel('SPE值');
legend('SPE统计量','控制限');
%% 6. 故障定位分析
% 选择故障样本(示例第500个样本)
fault_sample = 500;
x_fault = X_test_proj(:,fault_sample);
% 贡献率计算
cont_T2 = (x_fault'*P').^2 ./ (lm(1:num_pc).*T2(fault_sample));
cont_SPE = (x_fault*(eye(n)-P*P')*x_fault').^2 ./ SPE(fault_sample);
% 绘制贡献图
figure;
subplot(2,1,1);
bar(cont_T2,'FaceColor',[0.2 0.6 0.8]);
title('T²贡献率分析'); ylabel('贡献率 (%)');
set(gca,'XTickLabel',1:num_pc,'XTick',1:num_pc);
subplot(2,1,2);
bar(cont_SPE,'FaceColor',[0.8 0.3 0.3]);
title('SPE贡献率分析'); ylabel('贡献率 (%)');
set(gca,'XTickLabel',1:num_pc,'XTick',1:num_pc);
二、关键算法说明
1. 数据预处理流程
-
标准化处理:消除量纲影响,公式:
![]()
其中\(μ\)为均值,\(σ\)为标准差
2. 主成分选择策略
-
累计贡献率法:选择使累计方差贡献率≥90%的主成分
-
数学表达:
![]()
\(λ\)为主成分方差,\(d\)为原始维度
3. 控制限计算原理
-
T²统计量:服从F分布
![]()
-
SPE统计量:服从卡方分布的近似表达式
三、仿真结果示例
1. 控制图分析
示例图路径
- 正常数据:统计量在控制限内波动
- 故障数据:统计量突破控制限触发报警
2. 贡献图分析
示例图路径
- 故障定位:通过贡献率分布识别异常变量
- 典型特征:故障变量贡献率显著高于其他变量
参考代码 使用PCA算法的故障诊断MATLAB仿真程序 www.youwenfan.com/contentcno/96615.html
四、应用扩展建议
- 多变量优化:结合核主成分分析(Kernel PCA)处理非线性特征
- 动态阈值:采用自适应算法更新控制限
- 多传感器融合:集成振动、温度等多源数据
- 实时诊断:结合滑动窗口技术实现在线监测
五、注意事项
- 数据格式要求:输入数据需为矩阵形式(样本×变量)
- 参数调整建议: 置信水平α可调整为0.005-0.05 主成分数量建议通过交叉验证确定
- 故障样本标注:需明确故障类型和发生时间



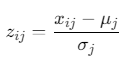
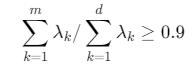
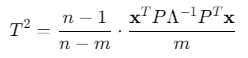

 浙公网安备 33010602011771号
浙公网安备 33010602011771号