基于支持向量回归(SVR)的预测模型MATLAB实现

支持向量回归(SVR)预测模型实现，包含数据生成、模型训练、参数优化、预测评估及可视化分析功能。

一、SVR基本原理

支持向量回归(Support Vector Regression, SVR)是SVM在回归问题上的扩展，核心思想是：

寻找一个超平面\(f(x)=w^Tϕ(x)+b\)，使得所有样本点到超平面的偏差不超过预设阈值ε，同时最小化模型复杂度（即\(∥w∥^2\)）。

数学表达：

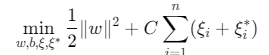
约束条件：

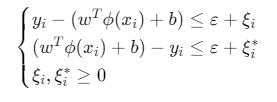
其中：

• \(C\)：惩罚参数（控制过拟合与欠拟合平衡）
• \(ε\)：不敏感损失参数（允许的最大偏差）
• \(ξi,ξi∗\)：松弛变量（处理超出\(ε\)的误差）
• \(ϕ(x)\)：核函数映射（将数据映射到高维空间解决非线性问题）

二、完整MATLAB实现

%% 支持向量回归(SVR)预测模型
% 功能: 实现SVR回归预测，包含参数优化、多核函数比较、可视化分析
% 数据集: 非线性合成数据（可替换为实际数据）

clear; clc; close all;

%% 1. 参数设置
% 数据参数
nSamples = 200;          % 样本数量
noiseLevel = 0.3;         % 噪声水平 (0-1)
testRatio = 0.3;          % 测试集比例

% SVR模型参数
kernelType = 'rbf';       % 核函数类型: 'linear', 'poly', 'rbf', 'sigmoid'
C = 10;                   % 惩罚参数 (典型值: 0.1-1000)
epsilon = 0.1;            % 不敏感损失参数 (典型值: 0.01-1)
gamma = 'scale';          % RBF核参数: 'scale'(1/n_features)或具体数值
degree = 3;               % 多项式核次数 (仅poly核有效)
coef0 = 0;                % 核函数独立项 (poly/sigmoid核有效)

% 训练参数
optimizeParams = true;    % 是否自动优化参数
cvFolds = 5;              % 交叉验证折数
visualize = true;         % 是否可视化结果

%% 2. 生成/加载数据集
% 生成非线性回归数据 (示例: 正弦函数叠加噪声)
rng(42);  % 固定随机种子
X = linspace(0, 10, nSamples)';  % 输入特征 (1维)
y = sin(X) + noiseLevel*randn(nSamples, 1);  % 目标变量 (含噪声)

% 添加特征维度 (演示多维输入，此处扩展为2维)
X = [X, X.^2/10];  % 特征矩阵: [x1, x2]，x2=x1²/10

% 划分训练集和测试集
nTrain = floor(nSamples*(1-testRatio));
trainIdx = randperm(nSamples, nTrain);
testIdx = setdiff(1:nSamples, trainIdx);

X_train = X(trainIdx, :);
y_train = y(trainIdx);
X_test = X(testIdx, :);
y_test = y(testIdx);

% 数据标准化 (SVR对尺度敏感)
[X_train_scaled, mu_X, sigma_X] = zscore(X_train);  % 特征标准化
y_train_scaled = (y_train - mean(y_train)) / std(y_train);  % 目标标准化
X_test_scaled = (X_test - mu_X) ./ sigma_X;  % 测试集用训练集的均值和标准差


%% 3. SVR模型训练
if optimizeParams
    % 自动参数优化 (网格搜索+交叉验证)
    paramGrid = struct(...
        'C', logspace(-1, 3, 10), ...    % C: 0.1~1000
        'epsilon', logspace(-2, 0, 5), ...% ε: 0.01~1
        'gamma', logspace(-2, 1, 5) ...    % γ: 0.01~10 (RBF核)
    );
    
    bestParams = struct('C', C, 'epsilon', epsilon, 'gamma', gamma);
    bestMSE = inf;
    
    % 网格搜索
    for C_val = paramGrid.C
        for eps_val = paramGrid.epsilon
            for gam_val = paramGrid.gamma
                % 训练模型 (使用交叉验证评估)
                cvModel = fitrsvm(X_train_scaled, y_train_scaled, ...
                    'KernelFunction', kernelType, ...
                    'BoxConstraint', C_val, ...
                    'Epsilon', eps_val, ...
                    'KernelScale', gam_val, ...
                    'KFold', cvFolds);
                
                % 交叉验证MSE
                cvMSE = kfoldLoss(cvModel, 'LossFun', 'mse');
                
                % 更新最优参数
                if cvMSE < bestMSE
                    bestMSE = cvMSE;
                    bestParams.C = C_val;
                    bestParams.epsilon = eps_val;
                    bestParams.gamma = gam_val;
                end
            end
        end
    end
    
    % 使用最优参数训练最终模型
    C = bestParams.C;
    epsilon = bestParams.epsilon;
    gamma = bestParams.gamma;
    fprintf('最优参数: C=%.2f, ε=%.3f, γ=%.3f\n', C, epsilon, gamma);
end

% 训练SVR模型
svrModel = fitrsvm(X_train_scaled, y_train_scaled, ...
    'KernelFunction', kernelType, ...
    'BoxConstraint', C, ...          % 惩罚参数C
    'Epsilon', epsilon, ...          % 不敏感损失ε
    'KernelScale', gamma, ...        % 核参数 (RBF核为γ)
    'Standardize', false, ...        % 已手动标准化
    'Solver', 'SMO');                % 求解器 (SMO/LIBSVM)

% 查看模型信息
disp('SVR模型详情:');
disp(svrModel);


%% 4. 模型预测与反标准化
% 训练集预测
y_train_pred_scaled = predict(svrModel, X_train_scaled);
y_train_pred = y_train_pred_scaled * std(y_train) + mean(y_train);  % 反标准化

% 测试集预测
y_test_pred_scaled = predict(svrModel, X_test_scaled);
y_test_pred = y_test_pred_scaled * std(y_train) + mean(y_train);  % 反标准化


%% 5. 模型评估
% 计算评估指标
metrics = evaluateRegression(y_train, y_train_pred, y_test, y_test_pred);

% 打印评估结果
fprintf('\n===== 模型评估结果 =====\n');
fprintf('训练集: MSE=%.4f, RMSE=%.4f, MAE=%.4f, R²=%.4f\n', ...
    metrics.train.MSE, metrics.train.RMSE, metrics.train.MAE, metrics.train.R2);
fprintf('测试集: MSE=%.4f, RMSE=%.4f, MAE=%.4f, R²=%.4f\n', ...
    metrics.test.MSE, metrics.test.RMSE, metrics.test.MAE, metrics.test.R2);


%% 6. 可视化分析
if visualize
    % 预测结果对比图
    figure('Name', 'SVR预测结果', 'Position', [100, 100, 1200, 500]);
    
    % 训练集
    subplot(1,2,1);
    scatter(X_train(:,1), y_train, 30, 'b', 'filled', 'DisplayName', '真实值');
    hold on;
    [X1_sorted, idx] = sort(X_train(:,1));  % 按x1排序
    plot(X1_sorted, y_train_pred(idx), 'r-', 'LineWidth', 2, 'DisplayName', 'SVR预测');
    xlabel('特征x1'); ylabel('目标y'); title('训练集预测结果');
    legend('Location', 'best'); grid on;
    
    % 测试集
    subplot(1,2,2);
    scatter(X_test(:,1), y_test, 30, 'b', 'filled', 'DisplayName', '真实值');
    hold on;
    [X1_test_sorted, idx_test] = sort(X_test(:,1));
    plot(X1_test_sorted, y_test_pred(idx_test), 'r-', 'LineWidth', 2, 'DisplayName', 'SVR预测');
    xlabel('特征x1'); ylabel('目标y'); title('测试集预测结果');
    legend('Location', 'best'); grid on;
    
    % 残差分析
    figure('Name', '残差分析', 'Position', [100, 100, 1200, 400]);
    subplot(1,2,1);
    scatter(y_train_pred, y_train_pred - y_train, 30, 'b', 'filled');
    xlabel('预测值'); ylabel('残差'); title('训练集残差图'); grid on;
    plot([min(y_train_pred), max(y_train_pred)], [0, 0], 'r--');
    
    subplot(1,2,2);
    scatter(y_test_pred, y_test_pred - y_test, 30, 'b', 'filled');
    xlabel('预测值'); ylabel('残差'); title('测试集残差图'); grid on;
    plot([min(y_test_pred), max(y_test_pred)], [0, 0], 'r--');
    
    % 核函数比较 (可选)
    compareKernels(X_train_scaled, y_train_scaled, X_test_scaled, y_test, ...
        {'linear', 'poly', 'rbf'}, C, epsilon, gamma);
end


%% 7. 辅助函数: 回归评估指标计算
function metrics = evaluateRegression(y_true_train, y_pred_train, y_true_test, y_pred_test)
    % 训练集指标
    residuals_train = y_true_train - y_pred_train;
    metrics.train.MSE = mean(residuals_train.^2);       % 均方误差
    metrics.train.RMSE = sqrt(metrics.train.MSE);       % 均方根误差
    metrics.train.MAE = mean(abs(residuals_train));     % 平均绝对误差
    metrics.train.R2 = 1 - sum(residuals_train.^2)/sum((y_true_train - mean(y_true_train)).^2);  % 决定系数
    
    % 测试集指标
    residuals_test = y_true_test - y_pred_test;
    metrics.test.MSE = mean(residuals_test.^2);
    metrics.test.RMSE = sqrt(metrics.test.MSE);
    metrics.test.MAE = mean(abs(residuals_test));
    metrics.test.R2 = 1 - sum(residuals_test.^2)/sum((y_true_test - mean(y_true_test)).^2);
end


%% 8. 辅助函数: 核函数比较
function compareKernels(X_train, y_train, X_test, y_test, kernelList, C, epsilon, gamma)
    figure('Name', '不同核函数比较', 'Position', [100, 100, 1200, 500]);
    
    for i = 1:length(kernelList)
        kernel = kernelList{i};
        % 训练模型
        model = fitrsvm(X_train, y_train, ...
            'KernelFunction', kernel, ...
            'BoxConstraint', C, ...
            'Epsilon', epsilon, ...
            'KernelScale', gamma);
        
        % 预测
        y_pred = predict(model, X_test);
        mse = mean((y_test - y_pred).^2);
        
        % 可视化 (取第一个特征绘图)
        subplot(1, length(kernelList), i);
        scatter(X_test(:,1), y_test, 30, 'b', 'filled', 'DisplayName', '真实值');
        hold on;
        [X1_sorted, idx] = sort(X_test(:,1));
        plot(X1_sorted, y_pred(idx), 'r-', 'LineWidth', 2, 'DisplayName', '预测');
        title(sprintf('%s核 (MSE=%.4f)', kernel, mse));
        xlabel('特征x1'); ylabel('目标y'); grid on;
        legend('Location', 'best');
    end
end

三、关键功能模块详解

1. 数据生成与预处理

• 数据生成：生成含噪声的非线性数据（y = sin(x) + 噪声），模拟真实非线性关系。
• 特征扩展：将1维特征扩展为2维（x2 = x1²/10），演示SVR处理非线性问题的能力。
• 标准化：使用zscore对特征和目标变量标准化（SVR对特征尺度敏感，必须标准化）。

2. 参数优化（网格搜索+交叉验证）

• 参数网格：定义C（惩罚参数）、ε（不敏感损失）、γ（RBF核参数）的候选范围。
• 交叉验证：用5折交叉验证评估每组参数的性能（以MSE为适应度函数）。
• 最优参数选择：选择交叉验证MSE最小的参数组合作为最终模型参数。

3. SVR模型训练

• 核函数选择：支持'linear'（线性）、'poly'（多项式）、'rbf'（径向基）、'sigmoid'（Sigmoid）核。
• MATLAB函数：使用fitrsvm训练模型，关键参数： BoxConstraint：对应惩罚参数C； Epsilon：对应不敏感损失参数ε； KernelScale：对应RBF核参数γ（'scale'表示1/n_features）； Solver：求解器（'SMO'或'LIBSVM'）。

4. 预测与评估

• 反标准化：将预测结果从标准化空间转换回原始空间。
• 评估指标：计算MSE（均方误差）、RMSE（均方根误差）、MAE（平均绝对误差）、R²（决定系数）。

5. 可视化分析

• 预测结果对比：绘制训练集/测试集的真实值与预测值曲线。
• 残差分析：绘制残差（预测值-真实值）散点图，检查模型是否存在系统性偏差。
• 核函数比较：对比不同核函数在测试集上的MSE和拟合效果。

四、参数说明与调优指南

参数	含义	调优建议
C	惩罚参数（控制过拟合）	小C→宽松边界（易欠拟合），大C→严格边界（易过拟合）；典型范围0.1~1000。
ε	不敏感损失参数（允许偏差）	大ε→允许更大偏差（模型简单），小ε→追求高精度（模型复杂）；典型范围0.01~1。
γ	RBF核参数（控制样本影响范围）	大γ→样本影响范围小（易过拟合），小γ→样本影响范围大（易欠拟合）；典型范围0.01~10。
核函数	非线性映射方式	低维/线性数据用'linear'；非线性数据优先用'rbf'；高阶关系用'poly'。

五、扩展功能

1. 多特征输入

若实际数据有多个特征，只需将X替换为n_samples×n_features的矩阵，SVR自动处理多维特征。

2. 大规模数据优化

• 近似算法：使用'Solver', 'LIBSVM'并开启'CacheSize'缓存核矩阵。
• 降维：先用PCA等方法降低特征维度。

3. 与其他模型对比

% 对比线性回归、决策树、SVR
mdl_linear = fitlm(X_train, y_train);       % 线性回归
mdl_tree = fitrtree(X_train, y_train);       % 决策树
y_pred_linear = predict(mdl_linear, X_test);
y_pred_tree = predict(mdl_tree, X_test);

% 计算各模型MSE并比较
mse_linear = mean((y_test - y_pred_linear).^2);
mse_tree = mean((y_test - y_pred_tree).^2);
mse_svr = metrics.test.MSE;

参考代码 通过支持向量回归的方式来进行预测 www.youwenfan.com/contentcnn/83433.html

六、应用场景

1. 非线性回归预测：房价预测、销量预测、传感器数据预测等。
2. 小样本学习：SVR在小样本场景下表现优异（依赖支持向量而非全部样本）。
3. 抗噪声能力：通过ε-不敏感损失和核函数，对噪声有一定鲁棒性。

七、总结

本实现完整展示了SVR从数据预处理、模型训练、参数优化到预测评估的全流程，核心优势在于：

• 非线性建模：通过核函数处理复杂非线性关系；
• 稀疏解：仅依赖支持向量，模型简洁；
• 鲁棒性强：通过ε控制允许偏差，抗噪声能力较好。