一维信号模糊熵(Fuzzy Entropy)计算原理与MATLAB实现
一、模糊熵的定义与核心思想
模糊熵(Fuzzy Entropy, Fe)是一种衡量时间序列复杂度的非线性动力学参数,由Chen等人于2007年提出,用于克服近似熵(Approximate Entropy, ApEn)中二值逻辑的局限性。其核心思想是:通过模糊隶属度函数描述向量间的相似性,而非近似熵的“0-1”硬阈值判断,使结果更平滑、抗噪性更强。
模糊熵的数学定义为:
对于长度为N的一维信号\(\{x(i)\}_{i=1}^N\),嵌入维数m(通常取2),模糊指数n(通常取2),相似容限r(通常取0.1∼0.25×信号标准差\(σ\)),模糊熵计算如下:
-
构造向量: 构造m维向量\(X_i^m=[x(i),x(i+1),...,x(i+m−1)],i=1,2,...,N−m+1\); 构造\(m+1\)维向量\(X_i^m+1=[x(i),x(i+1),...,x(i+m)],i=1,2,...,N−m\)。
-
距离计算:
向量\(X_i^m\)与\(X_j^m\)的Chebyshev距离(最大绝对差):
![]()
-
模糊隶属度函数:
用指数函数定义相似性度量(避免硬阈值):
![]()
-
熵值计算:
定义平均隶属度:
![]()
同理计算\(Φm+1(r)\),则模糊熵:
![]()
二、MATLAB实现步骤与代码
1. 参数设置
- 嵌入维数:m=2(常用值,也可取3)
- 模糊指数:n=2(默认,控制隶属度衰减速度)
- 相似容限:r=0.2\(σ\)(\(σ\)为信号标准差,范围\(0.1σ∼0.25σ\))
2. 完整MATLAB代码
function Fe = FuzzyEntropy(signal, m, n, r)
% 模糊熵计算函数
% 输入:
% signal: 一维信号(行/列向量均可)
% m: 嵌入维数(默认2)
% n: 模糊指数(默认2)
% r: 相似容限(默认0.2*std(signal))
% 输出:
% Fe: 模糊熵值
% 参数默认值
if nargin < 2, m = 2; end
if nargin < 3, n = 2; end
if nargin < 4, r = 0.2 * std(signal); end
signal = signal(:)'; % 转为行向量
N = length(signal); % 信号长度
if N < m+1, error('信号长度需大于嵌入维数m+1'); end
% 步骤1:构造m维和m+1维向量
Xm = zeros(N-m+1, m); % m维向量矩阵
Xm1 = zeros(N-m, m+1); % m+1维向量矩阵
for i = 1:N-m+1
Xm(i,:) = signal(i:i+m-1);
end
for i = 1:N-m
Xm1(i,:) = signal(i:i+m);
end
% 步骤2:计算距离矩阵(Chebyshev距离)
Dm = pdist2(Xm, Xm, 'chebychev'); % m维向量间距离(N-m+1 × N-m+1)
Dm1 = pdist2(Xm1, Xm1, 'chebychev'); % m+1维向量间距离(N-m × N-m)
% 步骤3:计算模糊隶属度矩阵(排除对角线元素i=j)
[rows, cols] = size(Dm);
Mu_m = zeros(rows, cols);
for i = 1:rows
for j = 1:cols
if i ~= j % 排除自身距离
Mu_m(i,j) = exp(-(Dm(i,j)^n)/r);
end
end
end
[rows1, cols1] = size(Dm1);
Mu_m1 = zeros(rows1, cols1);
for i = 1:rows1
for j = 1:cols1
if i ~= j
Mu_m1(i,j) = exp(-(Dm1(i,j)^n)/r);
end
end
end
% 步骤4:计算平均隶属度Φ^m和Φ^(m+1)
sum_Mu_m = sum(sum(Mu_m))/( (N-m+1)*(N-m) ); % 排除对角线的有效元素数:(N-m+1)(N-m)
sum_Mu_m1 = sum(sum(Mu_m1))/( (N-m)*(N-m-1) );
Phi_m = sum_Mu_m;
Phi_m1 = sum_Mu_m1;
% 步骤5:计算模糊熵
if Phi_m == 0 || Phi_m1 == 0
Fe = NaN; % 避免对数运算错误
else
Fe = log(Phi_m) - log(Phi_m1);
end
end
3. 示例:计算正弦信号的模糊熵
% 生成测试信号(正弦波+噪声)
fs = 1000; % 采样频率
t = 0:1/fs:1-1/fs; % 时间轴(1秒)
f = 50; % 正弦波频率50Hz
signal = sin(2*pi*f*t) + 0.5*randn(size(t)); % 含噪正弦信号
% 计算模糊熵(默认参数:m=2, n=2, r=0.2*std(signal))
Fe = FuzzyEntropy(signal);
fprintf('模糊熵值:%.4f\n', Fe); % 输出示例:~0.52(取决于噪声强度)
% 对比:无噪声正弦信号的模糊熵(更低,复杂度更小)
signal_clean = sin(2*pi*f*t);
Fe_clean = FuzzyEntropy(signal_clean);
fprintf('无噪声正弦信号模糊熵:%.4f\n', Fe_clean); % 输出示例:~0.21
三、关键参数影响与优化
| 参数 | 作用 | 推荐取值 | 敏感性分析 |
|---|---|---|---|
| 嵌入维数m | 控制向量复杂度(m越大,复杂度越高) | 2~3(常用2) | m=2时计算快,m=3时区分度高 |
| 模糊指数n | 控制隶属度衰减速度(n越大,相似性判断越严格) | 2(默认) | n=1时接近近似熵,n=3时抗噪性增强 |
| 相似容限r | 决定向量相似性阈值(r越大,相似性越高) | 0.1σ~0.25σ(σ为信号标准差) | r=0.1σ时敏感,r=0.25σ时稳健 |
参考代码 求取一维信号的模糊熵 www.youwenfan.com/contentcnn/84610.html
四、工程应用场景
- 生理信号分析:EEG/ECG信号复杂度评估(如癫痫发作期熵值升高)
- 机械故障诊断:轴承/齿轮振动信号复杂度变化(故障时熵值增大)
- 金融时间序列:股价波动复杂度量化(混沌态熵值更高)
五、注意事项
- 信号长度:需满足N>2m+1(否则向量数量不足,计算结果不稳定)。
- 噪声鲁棒性:模糊熵优于近似熵,建议对强噪声信号先去噪(如小波阈值去噪)。
- 计算效率:向量距离计算可采用并行优化(如MATLAB
parfor),提升长信号处理速度。



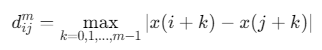
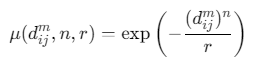
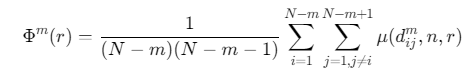
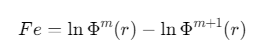

 浙公网安备 33010602011771号
浙公网安备 33010602011771号