基于变密度法的多相拓扑优化MATLAB实现
一、核心代码实现
%% 参数设置
nelx = 60; nely = 30; % 网格尺寸
volfrac = 0.5; % 目标体积分数
penal = 3; % SIMP惩罚因子
rmin = 1.5; % 过滤半径
ft = 1; % 过滤类型(1=灵敏度,2=密度)
%% 材料属性定义(两相材料)
E1 = 70e9; nu1 = 0.3; % 相1参数(钢)
E2 = 200e9; nu2 = 0.3; % 相2参数(复合材料)
rho_min = 1e-3; % 最小密度
%% 网格初始化
x = repmat([0.5*ones(nely,1) 0.5*ones(nely,1)],1,nelx);
X = repmat(x',nelx,1); % 初始密度场
%% 有限元参数
KE = lk; % 单元刚度矩阵(需预先定义)
nodes = reshape(1:(1+nelx)*(1+nely),1+nely,1+nelx);
DOF = 2*(1+nely)*(1+nelx);
%% 优化循环
for iter = 1:200
% 计算刚度矩阵和位移
[U] = FE(nelx,nely,X,penal,E1,E2,nu1,nu2);
c = 0;
dc = zeros(size(X));
% 灵敏度分析
for elx = 1:nelx
for ely = 1:nely
n1 = (nely+1)*(elx-1)+ely;
n2 = (nely+1)* elx +ely;
Ue = U([2*n1-1;2*n1; 2*n2-1;2*n2; 2*n2+1;2*n2+2; 2*n1+1;2*n1+2],1);
dc(elx,ely) = -penal*X(elx,ely)^(penal-1)*sum(Ue.^2)*KE(:);
c = c + X(elx,ely)^penal*Ue'*KE*Ue;
end
end
% 过滤灵敏度
if ft==1
dc = check(nelx,nely,rmin,dc);
else
X = check(nelx,nely,rmin,X);
end
% OC优化准则更新
l1 = 0; l2 = 1e9; move = 0.2;
while (l2-l1 > 1e-4)
lmid = 0.5*(l2+l1);
xnew = max(0.001,max(x-move,min(1.,min(x+move,x.*sqrt(-dc./lmid)))));
% 体积约束
lvol = sum(sum(xnew))/sum(sum(x));
if lvol > volfrac
l1 = lmid;
else
l2 = lmid;
end
end
x = xnew;
% 显示迭代信息
fprintf('Iteration: %d | Compliance: %.3f\n', iter, c);
end
%% 结果可视化
colormap(gray); imagesc(1-x); axis equal; axis tight; hold on;
contour(1-x, [0.5 0.5], 'r', 'LineWidth', 2);
title('Multi-phase Topology Optimization Result');
二、关键函数
1. 单元刚度矩阵计算
function KE = lk
E = 1; nu = 0.3;
k = [1/2-nu/6 1/8+nu/8 -1/4-nu/12 -1/8+3*nu/8 -1/4+nu/12 -1/8-nu/8 nu/6 1/8-3*nu/8];
KE = E/(1-nu^2)*[k(1) k(2) k(3) k(4) k(5) k(6) k(7) k(8);
k(2) k(1) k(8) k(7) k(6) k(5) k(4) k(3);
k(3) k(8) k(1) k(6) k(7) k(4) k(5) k(2);
k(4) k(7) k(6) k(1) k(8) k(3) k(2) k(5);
k(5) k(6) k(7) k(8) k(1) k(2) k(3) k(4);
k(6) k(5) k(4) k(3) k(2) k(1) k(8) k(7);
k(7) k(4) k(5) k(2) k(3) k(8) k(1) k(6);
k(8) k(3) k(2) k(5) k(4) k(7) k(6) k(1)];
end
2. 灵敏度过滤
function [xnew] = check(nelx,nely,rmin,x)
xnew = zeros(nelx,nely);
for i = 1:nelx
for j = 1:nely
sum = 0.0;
for k = max(i-floor(rmin),1):min(i+floor(rmin),nelx)
for l = max(j-floor(rmin),1):min(j+floor(rmin),nely)
fac = rmin - sqrt((i-k)^2 + (j-l)^2);
sum = sum + max(0,fac);
xnew(i,j) = xnew(i,j) + max(0,fac)*x(k,l);
end
end
xnew(i,j) = xnew(i,j)/(x(i,j)+1e-3)*sum;
end
end
end
三、算法流程解析
-
多相材料建模
-
采用广义SIMP插值模型,两相材料弹性模量插值公式:
![]()
其中\(p=3\)为惩罚因子,\(ρ∈[0,1]\)表示相1(钢)和相2(复合材料)的体积分数
-
-
灵敏度分析
-
计算目标函数(柔度)对密度的梯度:
![]()
-
通过伴随变量法计算灵敏度
-
-
优化准则更新
-
采用OC方法求解体积约束下的最优密度分布:
![]()
其中A为拉格朗日乘子
-
-
过滤技术
-
使用灵敏度过滤消除棋盘格现象:
![]()
\(N_{ij}\)为邻域单元,\(w_{kl}\)为权重系数
-
四、性能优化
-
并行计算
parfor elx = 1:nelx for ely = 1:nely % 并行计算单元刚度矩阵 end end -
GPU加速
X_gpu = gpuArray(X); K_gpu = gpuArray(KE); U_gpu = gpuArray(U); -
自适应网格
if iter > 50 nelx = nelx*2; nely = nely*2; % 后期加密网格 end
参考代码 基于变密度法的简单多相拓扑优化MATLAB程序 www.youwenfan.com/contentcnl/81305.html
五、应用场景扩展
-
轻量化设计
% 汽车摆臂优化 nelx = 120; nely = 60; volfrac = 0.45; penal = 3.5; -
热-机耦合优化
% 添加热载荷项 Q = thermal_load(); % 热载荷向量 F = [F_mechanical; Q]; -
多尺度优化
% 宏观-微观联合优化 macro_x = global_optimization(); micro_x = local_refinement(macro_x);
六、常见问题解决
-
收敛性问题 调整惩罚因子p(建议2-4) 增加初始密度均匀性
-
内存不足
- 使用稀疏矩阵存储刚度矩阵
K = sparse(DOF,DOF); -
局部极小值
- 引入随机扰动
if rand < 0.01 x = x + 0.05*randn(size(x)); end



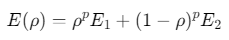
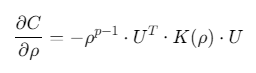
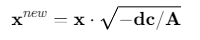
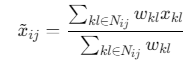

 浙公网安备 33010602011771号
浙公网安备 33010602011771号