二维变换

二维变换

为了在图像中指定一个位置，我们需要一种规范来实现。这种规范通过坐标系来设定。HALCON中使用了不同的坐标系。在此，我们解释二维中使用的坐标系。

像素是离散的，为了定位它们，我们有一个仅使用整数值的坐标系，即像素坐标系。为了获得超出像素网格的更高精度，我们需要浮点坐标，例如(3.6, 4.1) 。这就产生了亚像素精确坐标系。在HALCON中，有三种不同的亚像素坐标系实现方式：

  • 像素居中坐标，HALCON标准亚像素坐标系

  • 边缘居中坐标

  • 极坐标

其中前两种仅在坐标原点上有所不同，如下图所示。校准使得将图像坐标距离映射到实际世界距离成为可能。有关这些校准坐标的更多信息，请参考《解决方案指南III - C - 3D视觉》。

HALCON标准坐标系

像素精度坐标系

像素坐标系将图像视为由离散元素（像素）组成的网格。在HALCON中，我们将原点(0, 0)置于左上角像素的中间。现在，我们像在矩阵中一样指定像素坐标，确定其行和列。

请注意，对于大小为高度×宽度 = m×n像素的图像，这意味着行坐标值范围是从0到m - 1，列坐标值范围是从0到n - 1，如下图所示。

亚像素精度坐标系：像素中心

该坐标系的原点位于左上角图像像素的中心，坐标轴分别沿行(r)和列(c)方向。这样的设定包含了像素坐标系。图像的左上角坐标为(-0.5, -0.5) ，对于大小为高度×宽度 = m×n像素的图像，右下角坐标为(m - 0.5, n - 0.5)（=(m - 1 + 0.5, n - 1 + 0.5) ，记住坐标值从0开始）。这也意味着像素(k, l)覆盖的矩形区域为(k - 0.5, l - 0.5)、(k + 0.5, l - 0.5)、(k - 0.5, l + 0.5)、(k + 0.5, l + 0.5) 。这种设定被称为标准坐标系，也叫图像坐标系。

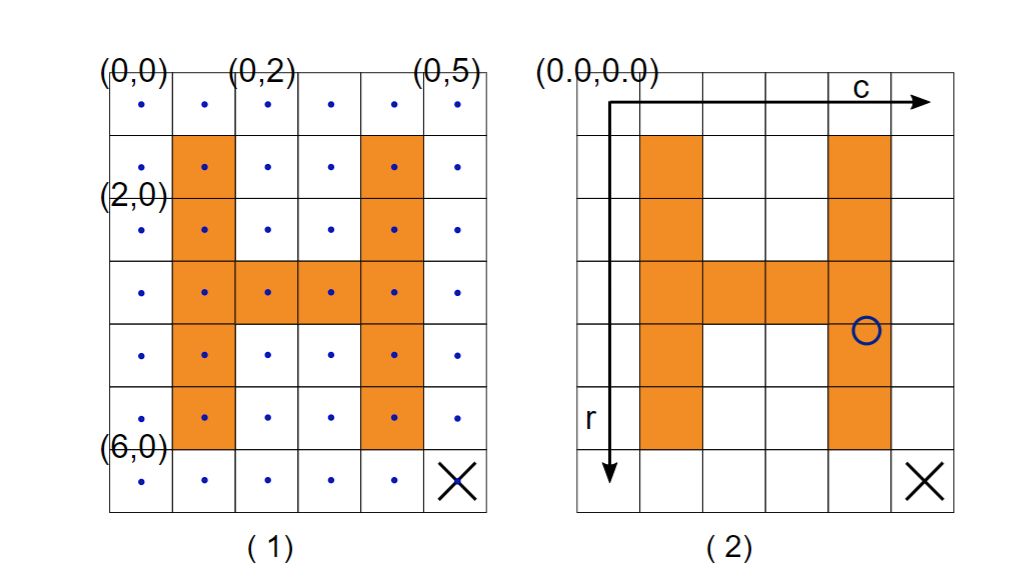
image-20250514170753505

上图为HALCON 标准像素和亚像素笛卡尔坐标系示意图。叉号表示图像右下角的像素。其中心坐标为 (6, 5)（在像素坐标系 (1) 中），(6.0, 5.0)（在标准亚像素坐标系 (2) 中）。圆心坐标为 (3.6, 4.1)。

HALCON非标准笛卡尔坐标系

如果我们将图像绕其原点旋转π/2（即90度），我们希望两幅图像边缘相接但不重叠。此外，对图像进行缩放时，不希望出现负的图像坐标。为此，原点(0,0)必须设置在图像的一个角上。这就引出了以下坐标系。

亚像素精度坐标系：边缘中心

在这个坐标系中，我们将原点设置在图像的左上角。因此，左上角像素的中心坐标为(0.5, 0.5) ，对于大小为高度×宽度 = m×n像素的图像，右下角坐标为(m, n) 。像素(k, l)覆盖的矩形区域为(k, l)、(k, l + 1)、(k + 1, l)、(k + 1, l + 1) 。

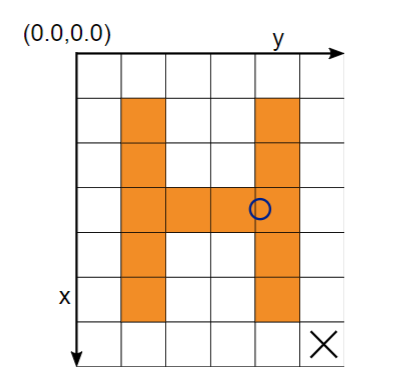
image-20250514171801185

展示HALCON非标准亚像素笛卡尔坐标系，叉号表示图像右下角像素，其中心坐标为(6.5, 5.5)，圆心坐标为(3.6, 4.1)

对于这个坐标系，旋转定义为数学上的正方向，即逆时针方向。π/2（90度）的旋转将第一轴（x轴）映射到第二轴（y轴）。相应地，轴的分配为行：x坐标，列：y坐标。

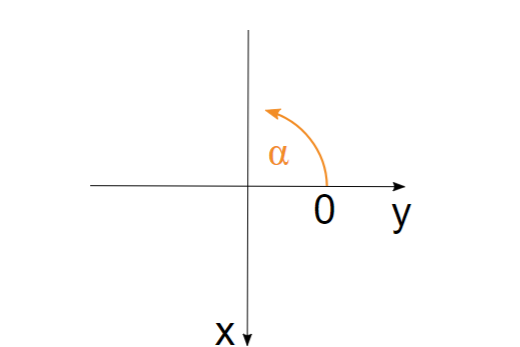
image-20250514172115291

使用边缘中心坐标系对旋转（α）进行可视化。

期望输入参数处于任意笛卡尔坐标系的算子

算子 AffineTransPoint2d 将由 homMat2D 给出的变换应用于点坐标。这意味着，AffineTransPoint2d 在两种笛卡尔坐标系中都能起作用，只要确保点和变换处于相同的坐标系中即可。

算子 AngleLl 和 AngleLx 可以接受以像素中心坐标形式输入的点，但返回的角度遵循数学上正方向（即逆时针方向）的旋转约定，并且以水平轴为 0，就如同在边缘中心坐标系中那样。

期望输入参数处于不同坐标系的算子

在 HALCON 中，也存在这样的情况：一个算子期望其输入处于不同的坐标系。一方面，对象期望处于其常用的坐标系，即标准坐标系。另一方面，对于变换矩阵 homMat2D，算子期望输入的是边缘中心坐标系下的坐标，因为在上述变换方面边缘中心坐标系具有优势。该算子将对象的坐标从 HALCON 的标准坐标系（原点位于左上角像素的中心）转换为边缘中心坐标系（原点位于左上角像素的左上角）。在用 homMat2D 进行变换之后，结果会被转换回标准坐标系。

在 HALCON 中，某些操作符要求输入参数来自不同的坐标系系统。具体来说：

  • 对象参数（如区域、轮廓等）默认使用 标准坐标系（Standard Coordinate System），原点位于左上角像素的中心，即 (0.5, 0.5)。

  • 变换矩阵 homMat2D 则需基于 边缘中心坐标系（Edge-centered Coordinate System）定义，原点位于左上角像素的左上角，即 (0, 0)。

内部处理流程

  1. 输入转换：操作符自动将对象的坐标从标准坐标系转换为边缘中心坐标系。

    • 例如，若对象的某个点坐标为 (x, y)，转换时会执行 x_edge = x - 0.5 和 y_edge = y - 0.5。

  2. 应用变换：在边缘中心坐标系下，使用 homMat2D 对对象进行仿射变换。

  3. 输出转换：将变换后的坐标从边缘中心坐标系转回标准坐标系。

    • 反向转换公式为 x_std = x_transformed + 0.5 和 y_std = y_transformed + 0.5。

典型操作符示例

  • AffineTransRegion（区域仿射变换）

    • 输入区域基于标准坐标系，变换矩阵基于边缘中心坐标系，输出区域仍为标准坐标系。

  • AffineTransContourXld（轮廓仿射变换）

    • 确保轮廓变换时几何精度不受像素插值影响。

技术意义

  • 边缘中心坐标系的优势：

    • 避免因像素中心对齐导致的亚像素误差，使平移、旋转等变换更精确。

    • 简化连续变换的矩阵合成（如 hom_mat2d_compose）。

  • 开发注意事项：

    • 若手动定义 homMat2D，需确保其参数在边缘中心坐标系下计算。

    • 使用 area_center 或 get_contour_xld 获取对象坐标时，结果默认在标准坐标系中。

坐标系转换公式总结

操作方向 转换公式
标准 → 边缘中心 x_edge = x_std - 0.5
  y_edge = y_std - 0.5
边缘中心 → 标准 x_std = x_edge + 0.5
  y_std = y_edge + 0.5

常见问题

Q：为何不统一使用单一坐标系？ A：标准坐标系符合直觉（像素中心为坐标点），而边缘中心坐标系更适合几何变换（避免半个像素偏移导致的累积误差）。两者分工明确，确保算法鲁棒性。

Q：如何验证变换矩阵的正确性？ A：可通过 hom_mat2d_identity 生成单位矩阵，手动平移 (0.5, 0.5) 后观察对象是否精确移动一个像素。

支持的操作符列表

  • AffineTransContourXld

  • AffineTransImage

  • AffineTransImageSize

  • AffineTransPixel

  • AffineTransPolygonXld

  • AffineTransRegion

  • ProjectiveTransContourXld

  • ProjectiveTransImage

  • ProjectiveTransImageSize

  • ProjectiveTransPixel

  • ProjectiveTransRegion

矩阵坐标系转换示例

若需将像素中心坐标系的变换矩阵转换为边缘中心坐标系：

 HomMat2dTranslate(HomMat2D, 0.5, 0.5, HomMat2DTmp)  
 HomMat2dTranslateLocal(HomMat2DTmp, -0.5, -0.5, HomMat2DAdapted)  

注意，上述以projective_开头的算子使用的是投影变换矩阵。这些变换矩阵，例如，可以从 3D 相机位姿中获取。这样做时，所使用的矩阵是 3D 坐标系中 xy 平面的投影。相应地，轴的分配为行：y 坐标，列：x 坐标，因此坐标需要进行转换。

基于形状的匹配和基于相关性的匹配

基于形状匹配（如FindGenericShapeModel ）的结果以边缘居中坐标系给出。返回的匹配结果已经过变换。相应的单应变换矩阵可使用 GetGenericShapeModelResult 检索。

基于相关性匹配（如FindNccModel和FindNccModels ）的结果同样在边缘居中坐标系中计算，不过变换参数会单独返回。利用这些结果，可以创建一个变换矩阵homMat2D，该矩阵可直接应用于如AffineTransContourXld 以及上述“适用于不同坐标系参数的算子”段落中列出的其他算子。

为显示基于相关性匹配找到的结果，我们强烈建议使用dev_display_ncc_matching_results 过程。

在以下图像中，我们给出一个示例，展示在正确和错误的坐标系中使用变换矩阵时，显示的匹配结果可能是什么样的。对于后者（如图(3)所示），变换矩阵也是在像素居中坐标系中给出的，因此AffineTransContourXld 显示的匹配结果会有0.5像素的偏差。注意，这种影响仅在涉及旋转时可见。

image-20250514203305966

回形针的原始图像(1)，输入坐标正确时匹配的一部分(2)，以及输入坐标错误时的匹配情况。

非笛卡尔坐标系

亚像素精确坐标系：极坐标

在极坐标系中，点通过距离和角度来定义。该距离称为径向坐标，是相对于固定点（极点）给出的。角坐标是相对于已定义的轴（极轴）给出的。在HALCON中，极点由(Row, Column)指定，极轴为水平轴。角坐标以弧度表示。

通过PolarTransImageExt进行变换后，输出图像中的左上角像素始终对应于输入图像中由radiusStart和angleStart指定的点。类似地，输出图像中的右下角像素对应于输入图像中由radiusEnd和angleEnd指定的点。在通常模式下（angleStart < angleEnd 且 radiusStart < radiusEnd ），极坐标变换按数学正方向（逆时针方向）进行。此外，半径较小的点位于输出图像的上部。通过适当地交换这些参数的值（例如，angleStart > angleEnd 或 radiusStart > radiusEnd ），可以实现输出图像的任何所需方向。

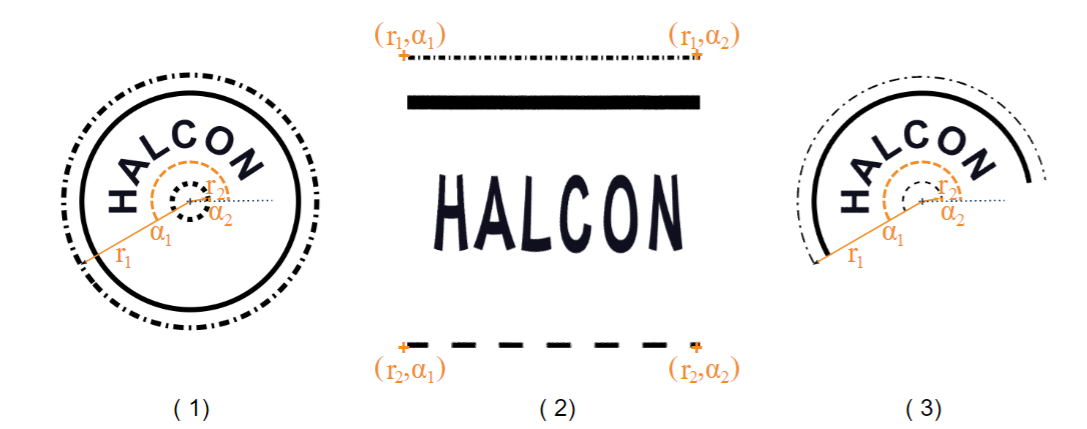
image-20250514203931153

例如，我们展示一个由其极点(行, 列)(+)、极轴(...)、两个角坐标angleStart(α1)、angleEnd(α2)以及两个径向坐标radiusStart(r1)、radiusEnd(r2)定义的环形弧。(1) 原始图像以及定义环形弧的参数。(2) 环形弧，在一个图中显示，其中极坐标形成通过PolarTransImageExt获得的等距网格。(3) 在原始图像表示中的环形弧。笛卡尔坐标通过对图像(2)应用PolarTransImageInv获得。原点位于左上角像素的中心。

极坐标操作符

  • PolarTransImageExt

  • PolarTransImageInv

  • PolarTransRegion

  • PolarTransRegionInv

  • PolarTransContourXld

  • PolarTransContourXldInv

  • PolarTransImage（旧版）

图像、区域与模型的坐标系继承

类型 坐标系继承规则
图像（含裁剪域） 继承原始图像的坐标系（原点与坐标值不变）。
区域（Region） 同上。
模型 可能具有局部坐标系（如 CreateGenericShapeModel 创建的模型以ROI重心为原点）。

标定坐标系

  • 目的：将像素坐标转换为真实世界坐标（需相机标定）。

  • 应用场景：三维视觉（3D Vision）、测量等。

  • 参考文档：

    • 《Solution Guide III-C - 3D Vision》（标定与三维重建方法）。

    • 《Solution Guide II-B - Matching》（模型局部坐标系详解）。

技术注释

  • 边缘中心坐标系的优势：消除像素对齐误差，确保几何变换（如连续旋转）的数学一致性。

  • 开发建议：

    • 使用 set_system('coord_system', 'edge') 临时切换坐标系。

    • 处理标定坐标时，优先使用 image_points_to_world_plane 等接口转换坐标。

算子列表

  1. AffineTransPixel：对像素坐标应用任意二维仿射变换。

  2. AffineTransPoint2d：对点应用任意二维仿射变换。

  3. DeserializeHomMat2d：反序列化一个序列化的齐次二维变换矩阵。

  4. HomMat2dCompose：将两个齐次二维变换矩阵相乘。

  5. HomMat2dDeterminant：计算齐次二维变换矩阵的行列式。

  6. HomMat2dIdentity：生成表示恒等二维变换的齐次变换矩阵。

  7. HomMat2dInvert：求齐次二维变换矩阵的逆。

  8. HomMat2dReflect：向齐次二维变换矩阵添加反射变换。

  9. HomMat2dReflectLocal：向齐次二维变换矩阵添加局部反射变换。

  10. HomMat2dRotate：向齐次二维变换矩阵添加旋转变换。

  11. HomMat2dRotateLocal：向齐次二维变换矩阵添加局部旋转变换。

  12. HomMat2dScale：向齐次二维变换矩阵添加缩放变换。

  13. HomMat2dScaleLocal：向齐次二维变换矩阵添加局部缩放变换。

  14. HomMat2dSlant：向齐次二维变换矩阵添加倾斜变换。

  15. HomMat2dSlantLocal：向齐次二维变换矩阵添加局部倾斜变换。

  16. HomMat2dToAffinePar：从齐次二维变换矩阵计算仿射变换参数。

  17. HomMat2dTranslate：向齐次二维变换矩阵添加平移变换。

  18. HomMat2dTranslateLocal：向齐次二维变换矩阵添加局部平移变换。

  19. HomMat2dTranspose：转置齐次二维变换矩阵。

  20. HomMat3dProject：将仿射三维变换矩阵投影为二维投影变换矩阵。

  21. HomVectorToProjHomMat2d：使用给定的点对应关系计算齐次变换矩阵。

  22. PointLineToHomMat2d：根据点到线的对应关系近似仿射变换。

  23. ProjectiveTransPixel：使用齐次投影变换矩阵投影像素坐标。

  24. ProjectiveTransPoint2d：使用投影变换矩阵投影齐次二维点。

  25. SerializeHomMat2d：序列化齐次二维变换矩阵。

  26. VectorAngleToRigid：根据点和角度计算刚性仿射变换。

  27. VectorFieldToHomMat2d：根据位移矢量场近似仿射映射。

  28. VectorToAniso：根据点对应关系近似各向异性相似变换。

  29. VectorToHomMat2d：根据点对应关系近似仿射变换。

  30. VectorToProjHomMat2d：使用给定的点对应关系计算投影变换矩阵。

  31. VectorToProjHomMat2dDistortion：使用给定的图像点对应关系计算投影变换矩阵和径向畸变系数。

  32. VectorToRigid：根据点对应关系近似刚性仿射变换。

  33. VectorToSimilarity：根据点对应关系近似相似变换。

posted @ 2025-05-15 16:06  明理  阅读(240)  评论(0)    收藏  举报