连杆结构上的欧拉-牛顿法迭代动力学算法

以下每个量都是在各自坐标系内观察得到的值，同时小括号表示取某个方向上的分量作为一个新的向量。

外推

从基座开始，对每个连杆使用牛顿-欧拉方差，逐个计算连杆的速度和加速度。

\(w_{i+1}=Rw_i+\dot{\theta}_{i+1}(z)\)

\(\dot{w}_{i+1}=R\dot{w}_i+Rw_i \times \dot{\theta_i}(z) + \ddot{\theta}_{i+1}(z)\)

\(\dot{v}_{i+1}=R(\dot{w_i} \times P_{i+1} + w_i \times (w_i \times P_{i+1}) + \dot{v}_i)\)

\(\dot{v}_{C_{i+1}}=\dot{w_{i+1}} \times P_{C_{i+1}} + w_{i+1} \times (w_{i+1} + P_{C_{i+1}}) + \dot{v}_{i+1}\)

\(F_{i+1}=m_{i+1}\dot{v}_{C_{i+1}}\)

\(N_{i+1}=I_{C_{i+1}}\dot{w}_{i+1}+w_{i+1} \times I_{C_{i+1}} w_{i+1}\)

内推

从连杆n开始，利用外推过程中得到的惯性力，计算各个连杆上的力和力矩、关节驱动力

\(f_i = Rf_{i+1} + F_i\)

\(n_i = N_i + Rn_{i+1} + P_{C_i} \times F_i + P_{i+1} \times Rf_{i+1}\)

\(\tau_{i} = n_i^{T_i}(z)\)

初值

通常来说，底座是不动的，所以

\(w_0 = 0\), \(\dot{w}_0 = 0\)

\(v_0 = 0\)

而重力也是不能忽略的，那就令\(\dot{v}_0 = g\)即可，等效于机器人正在以1g的加速度在做向上加速运动。一般而言，写成向量是\(\dot{v}_0=g(y)\)。

末端执行器上可能有存在力和力矩，有

\(f_{n+1} = f_{final}\), \(n_{i+1} = n_{final}\)

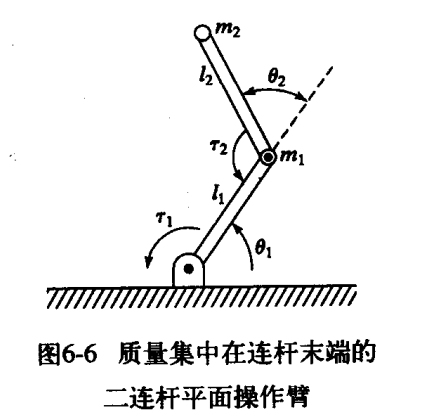
栗子-二连杆