数据结构期末复习(1)树
目录
求叶子结点的个数
二叉树的存储
二叉树的遍历
1、广度优先遍历(层次遍历)vs 深度优先遍历
2、先序 vs 中序 vs 后序遍历(属于深度优先遍历)
2.1 由中序+先序/后序推出二叉树
2.2 由二叉树推出先序/中序/后序遍历的顺序
3、二叉树的递归遍历 vs 非递归遍历 ?
https://blog.csdn.net/qq_23009153/article/details/78269520
将树转换为二叉树
特殊的二叉树类型:
哈夫曼树/最优二叉树
满二叉树vs完全二叉树
二叉排序树/二叉搜索树/二叉查找树
线索二叉树
最小生成树
求叶子结点的个数
一定要记住的两条公式:
①N=n0+n1+n2+...
②N=0*n0+1*n1+2*n2+...+1
(其中,N为结点数总数;n0为度为0的结点数,即叶子结点;n1位度为1的结点数,以此类推...)
eg.

【补充】
度:节点所拥有的子树的数目称为该节点的度
二叉树的遍历
带权无向图G(顶点分别为V1,V2,V3,V4,V5,V6)的邻接矩阵是A

要求: (1)画出图G
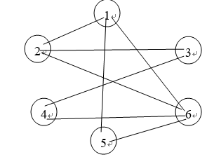
注意:无向图的邻接矩阵是对称的,因此如果要根据邻接矩阵画图,可以直接只看上三角或下三角(不然很浪费时间)
(2)分别写出从V1出发的深度优先遍历序列和广度优先遍历序列。
深度:1,2,3,4,6,5
广度:1,2,5,6,3,4
解释:
(1)求深度
设从结点v1出发,一直沿着所连的路走下去即可:v1→v2→v3→v4→v6→v5
*假设图中v2除了与v1相连外,不再与图中其他结点相连怎么办?
A:直接从v2返回到v1,再从v1开始对其他结点的遍历(v2只要能遍历到就可以了)
(2)求广度
求广度遍历的次序,实质上是看一个结点与哪些结点相连。
设从结点v1出发 → 相当于先访问了v1,
v1与v2、v5、v6相连 → 于是在访问v1后,会先遍历到v2、v5、v6
然后看v2、v5、v6分别与哪些结点直接相连:
v2:与v1,v3,v6相连,其中v3还没有被访问过 → 遍历v3
v5:与v1,v6相连,都被访问过了
v6:与v1,v4,v5相连,其中v4还没有被访问过 → 遍历v4
最终的广度优先遍历次序:v1 v2 v5 v6 v3 v4
哈夫曼树 / 最优二叉树
【哈夫曼树的构造】——权值从小到大排序,两两组合权值最小值,直到组成一棵二叉树
https://blog.csdn.net/yushupan/article/details/82735773
【求哈夫曼树的带权路径】——权值W = 各叶子结点权值*距离根节点的距离 之和(需要计算的权值点不包括中途生成的权值之和,即所有的父节点)
https://www.jianshu.com/p/35cf51516fe5
哈夫曼树的结点数关系:
由于哈夫曼树中没有度为1的结点。 只有度为0和度为2的结点。(树中的度:表示有几个孩子)
则一棵有n个叶子结点的哈夫曼树共有2n-1个结点。
eg.以数据集{4,5,6,7,10,12,18}为叶结点权值所构造的哈夫曼树,其带权路径长度为(165 )。
A:

带权路径长度:(4+5)*4+(6+7)*3+10*3+12*2+18*2=165
(再次强调——带权路径长度:只算叶子结点!)
哈夫曼编码
描述的是到达哈夫曼树中的一个元素所需要走的路径。其中,0表示向树的左儿子方向移动,1表示向树的右儿子方向移动。
eg.

哈夫曼树如下图所示:
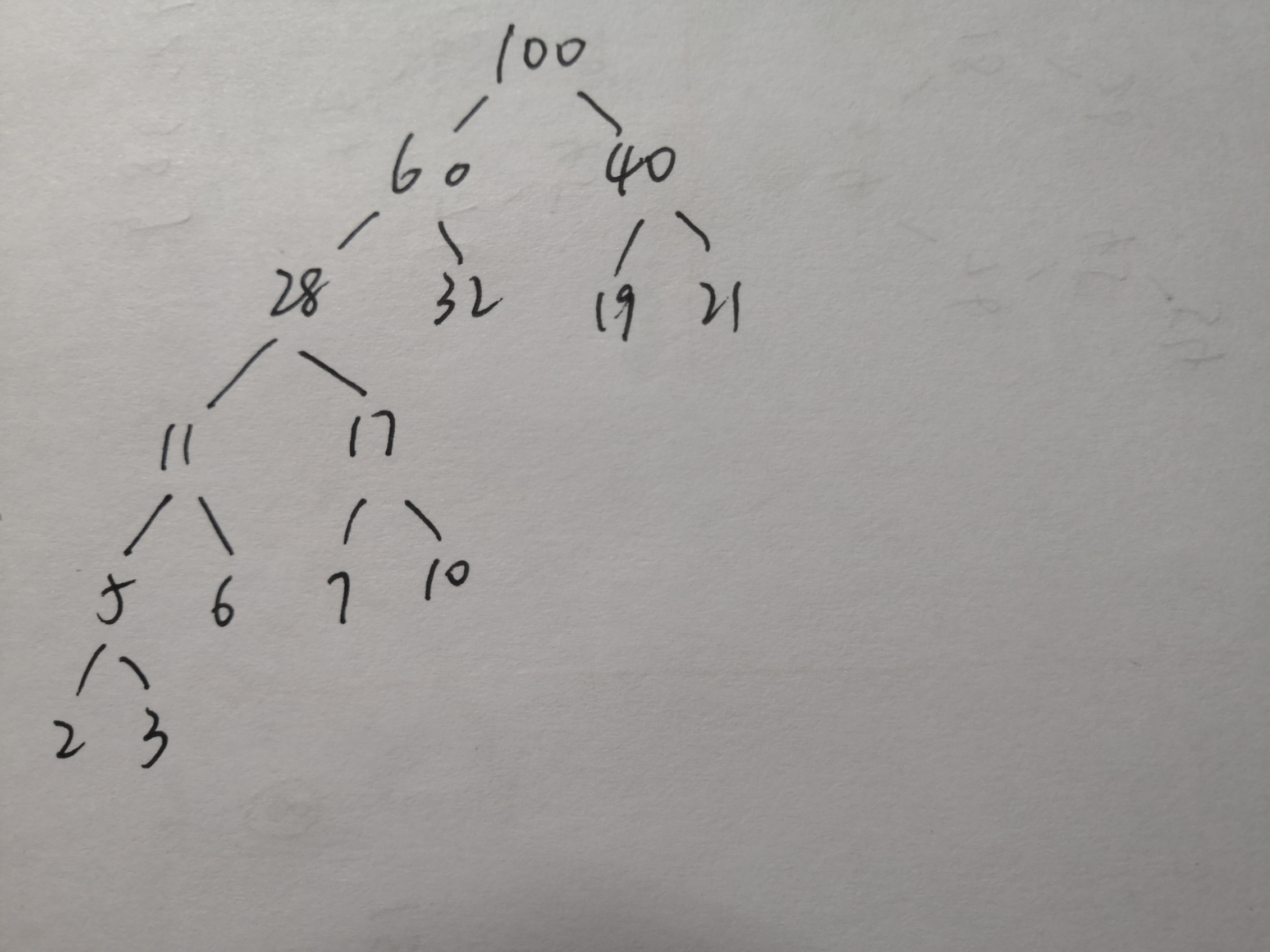
各个电文对应的频文就是哈夫曼树中需要找的结点
A:17
分析过程:
从100开始左行到60→0
从60开始左行到28→0
从28开始右行到17→1
所以A的哈夫曼编码为:001
其余频文同理。
eg.

(下面这个解释我也不太确定对不对,感觉如此?)
↑特别注意:
哈夫曼树中得到的结点权值之和不能和其他的结点(即不是权值之和的结点)再次组合成权值之和
具体到本题来说:本题中5和10得到15,而本来权值中也有15,这怎么办呢?
5和10得到的15属于权值之和,这个权值之和应该与另一个权值之和组合
而原来权值中就有的15要与12组合

二叉树的存储结构
(1)顺序存储
(2)链表存储
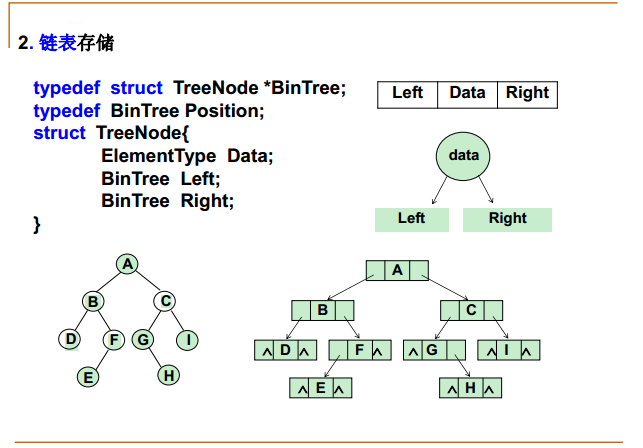
一棵有n个结点的二叉树,除了根结点之外,其余每个结点均有一个出自其双亲的指针域的指向该结点的指针,
因此,共有n-1个指针域非空。
指针域的总数目为2n,所以恰好有n+1个空指针域。
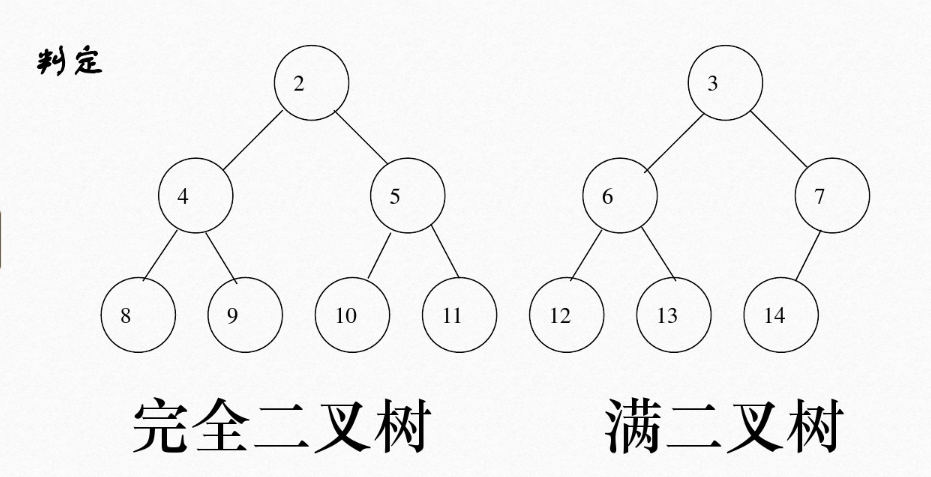
满二叉树&完全二叉树
满二叉树是特殊的二叉树
二叉树的遍历
前序遍历
中序遍历
后序遍历
(补充mooc图)
//仅提供前序和后续遍历的序列是不能反推出二叉树的
(未完待续)
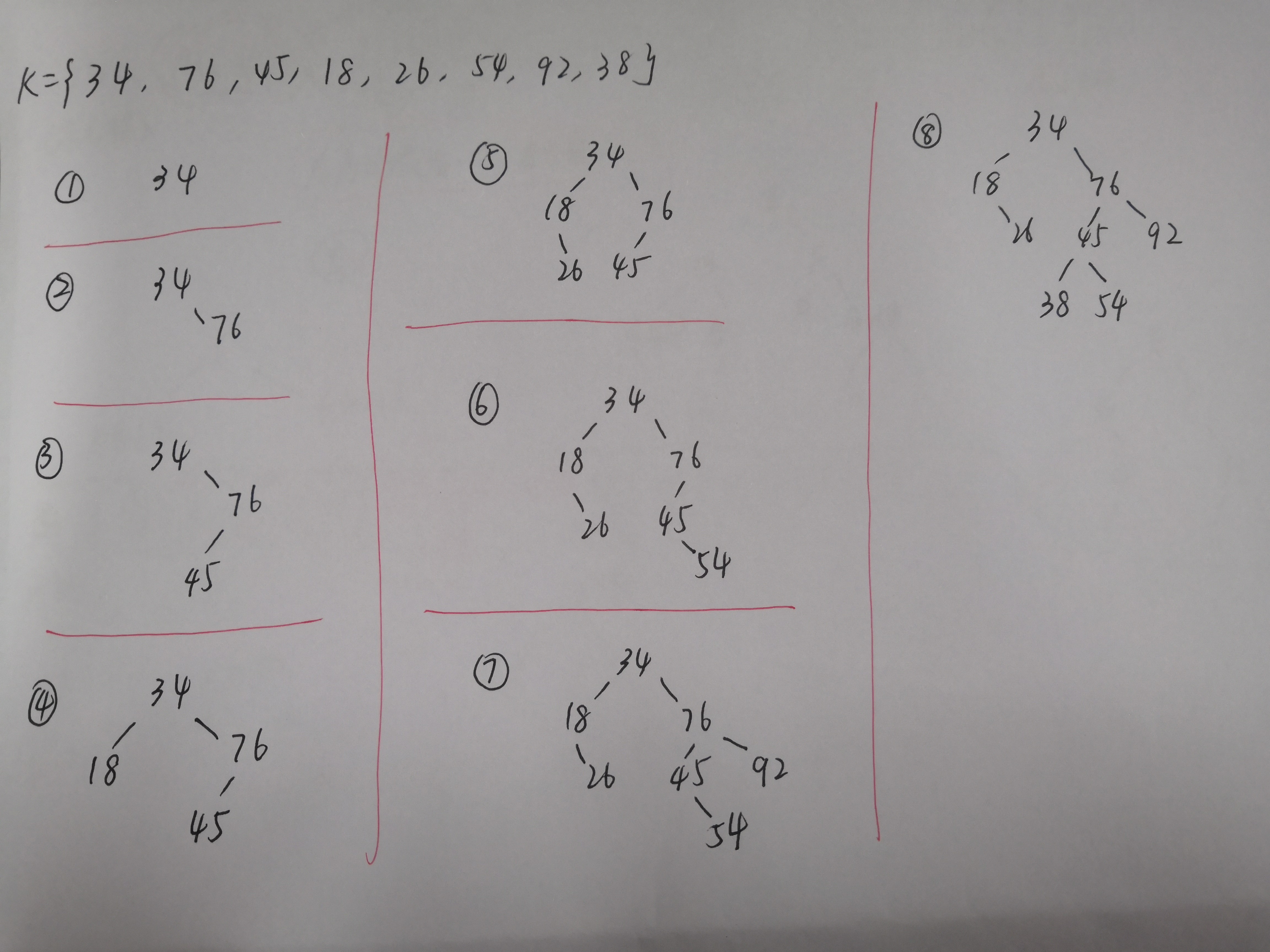
二叉排序树

二叉排序树的构建步骤:
将关键字集合中的第一个作为整个二叉排序树的根节点
取第2个关键字,如果它比根节点大,则作为根节点的右孩子;如果比根节点小,就作为根节点的左孩子;
……(后序步骤同上)
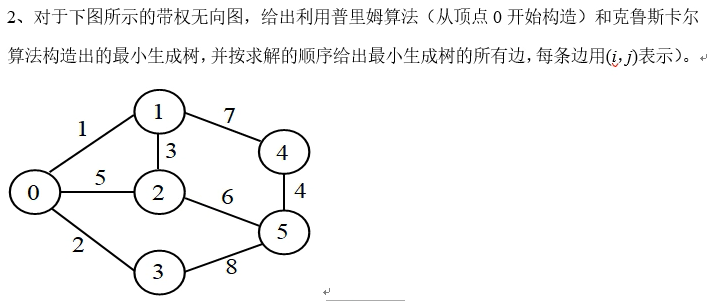
(图的)最小生成树
相关知识点:Prim算法、Kruskal算法
此部分请看↓
https://www.cnblogs.com/HelenBlog/p/13111671.html
留一道例题:
将树转化为二叉树
(1)加线。在所有兄弟结点之间加一条连线。
(2)去线。树中的每个结点,只保留它与第一个孩子结点的连线,删除它与其它孩子结点之间的连线。
(3)层次调整。以树的根节点为轴心,将整棵树顺时针旋转一定角度,使之结构层次分明。
(注意:第一个孩子是结点的左孩子,兄弟转换过来的孩子是结点的右孩子)
(注意:如果有结点只有一个孩子结点,则在转化为二叉树时,这个孩子结点将变为此节点的左孩子结点)

将森林转化为二叉树
(1)把每棵树转换为二叉树。
(2)第一棵二叉树不动,从第二棵二叉树开始,依次把后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子,用线连接起来。

eg.
把下列森林转换为二叉树(写出过程)
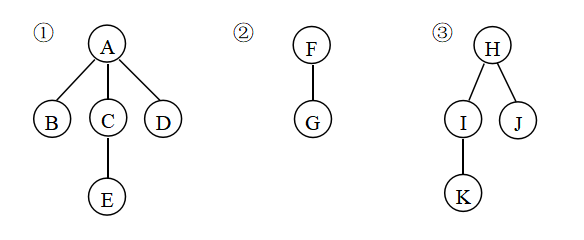
A:
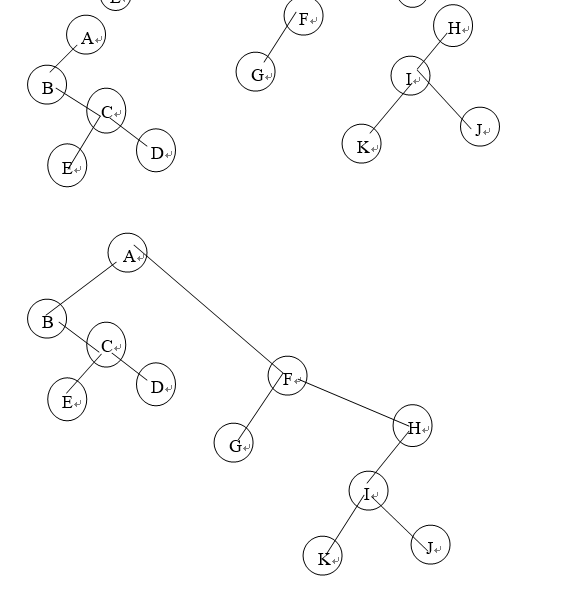
二叉树转换为森林(感觉这个考的较少)
假如一棵二叉树的根节点有右孩子,则这棵二叉树能够转换为森林,否则将转换为一棵树。
(1)从根节点开始,若右孩子存在,则把与右孩子结点的连线删除。再查看分离后的二叉树,若其根节点的右孩子存在,则连线删除…。直到所有这些根节点与右孩子的连线都删除为止。
(2)将每棵分离后的二叉树转换为树。
(见图:将同时有左右孩子的结点的右孩子结点的连线删去,再直接将孩子结点们(兄弟)相连,就可以将森林转化为树)

最小生成树
一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。(n个结点,n-1条边)
具体请看期末复习笔记(2)图:https://www.cnblogs.com/HelenBlog/p/13111671.html
(涉及Prim算法和Kruskal算法)
二叉排序树(二叉查找树、二叉搜索树)BST
二叉查找树:
根节点的值大于其左子树中任意一个节点的值,小于其右节点中任意一节点的值,这一规则适用于二叉查找树中的每一个节点。
(或者是一棵空树)
参考:https://blog.csdn.net/rodman177/article/details/89771156
二叉搜索树作为一种经典的数据结构,它既有链表的快速插入与删除操作的特点,又有数组快速查找的优势
二叉搜索树能够高效地进行如下操作:
1.插入一个数值
2.查询是否包含某个数值
3.删除某个数值
不论哪一种操作,所花的时间都和树的高度成正比。因此,如果共有n个元素,那么平均每次操作需要O(logn)的时间。
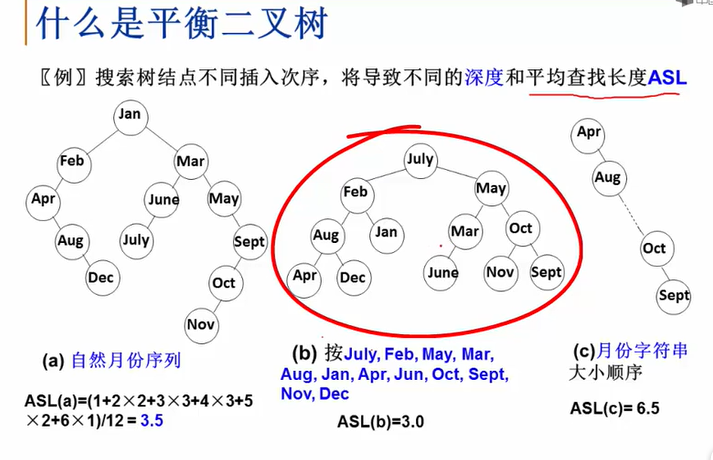
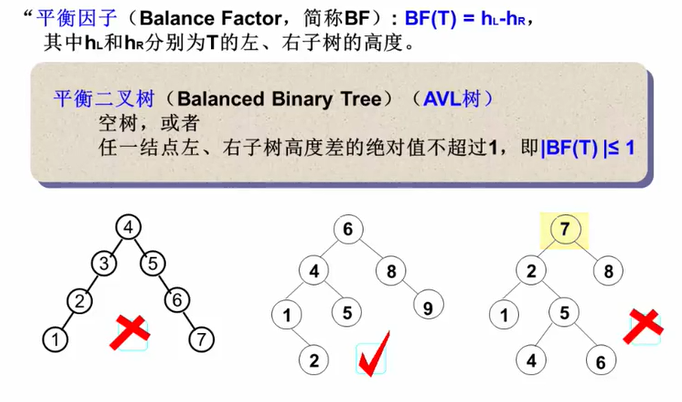
平衡二叉树(AVL树)
平衡二叉树也是一种搜索树。
(即左子树比根节点小,右子树比根节点大)
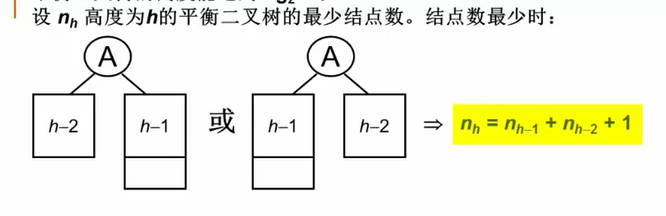
(总结点数=左儿子结点数+右儿子结点数+1)
将二叉树调整为平衡二叉树:
https://www.bilibili.com/video/BV1JW411i731?p=44


 浙公网安备 33010602011771号
浙公网安备 33010602011771号