数据结构期末复习(2)图
邻接矩阵&邻接表 表示图
邻接矩阵表示:
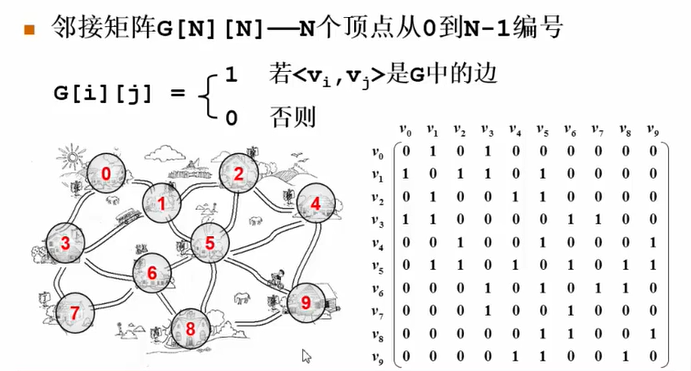
一般用邻接矩阵表示稠密图,因为表示稀疏图会造成空间和时间上的浪费
邻接矩阵存储空间为n2,所以存储空间只和顶点个数有关
若想在邻接矩阵中表示权重,则可以将矩阵中的1改为权重的值即可
邻接图表示:
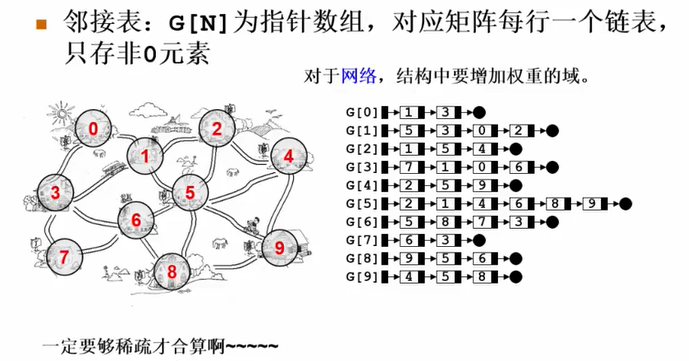
一般用邻接表表示稀疏图
邻接表存储空间为n+e
拓扑排序
举个栗子:先修课与后修课

AOV&AOE
AOE网络:一般用来安排项目的工序
【软考知识点】PERT图(计算题)
找出事件发生的顺序。
正推:所有时间的最早开始时刻
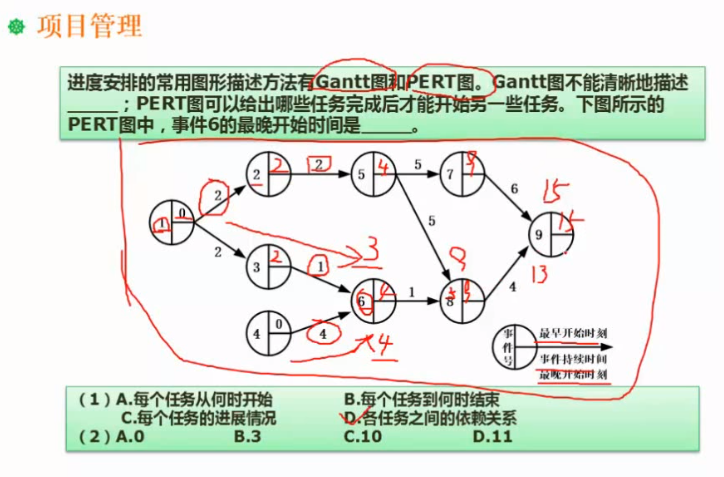
事件2的最早开始时刻=事件1的最早开始时刻+事件1持续时间=0+2=2
事件3的最早开始时刻=事件1的最早开始时刻+事件1持续时间=0+2=2
事件6的最早开始时刻=Max(事件3的最早开始时刻+事件3持续时间,事件4的最早开始时刻+事件4持续时间)=事件4的最早开始时刻+事件4持续时间=0+4=4
【要注意像事件6这种:有多个事件进行完毕,才能进行的下一个的事件的 最早开始时间】
(图中其余事件的求法同理)
逆推:所有时间的最晚开始时刻
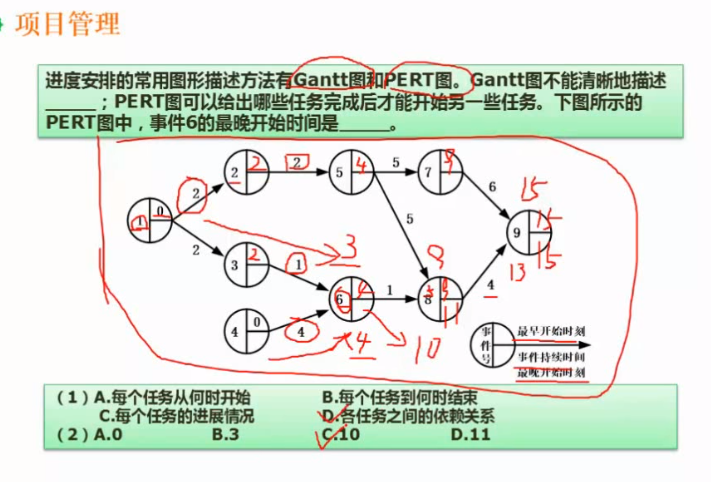
已知最后一个事件(事件9)的最早开始时间=最晚开始时间=15
所以开始逆推
事件8的最晚开始时间=事件9的最晚开始时间-事件8持续时间=15-4=11
→事件6的最晚开始时间=事件8的最晚开始时间-事件6持续时间=11-1=10
→故选C
图的最小生成树
最小生成树:
现在假设有一个很实际的问题:我们要在n个城市中建立一个通信网络,则连通这n个城市需要布置n-1一条通信线路,这个时候我们需要考虑如何在成本最低的情况下建立这个通信网?
于是我们就可以引入连通图来解决我们遇到的问题,n个城市就是图上的n个顶点,然后,边表示两个城市的通信线路,每条边上的权重就是我们搭建这条线路所需要的成本,所以现在我们有n个顶点的连通网可以建立不同的生成树,每一颗生成树都可以作为一个通信网,当我们构造这个连通网所花的成本最小时,搭建该连通网的生成树,就称为最小生成树。
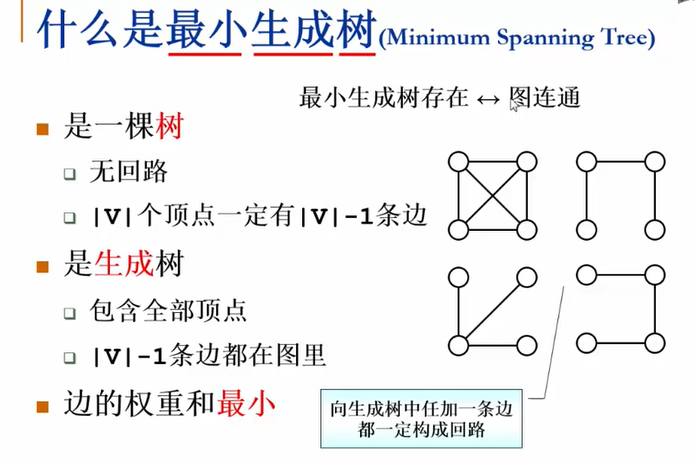
求最小生成树的算法,本质上都是贪心算法。(每一步都要最好——求最小生成树时,求权重最小)
(1)Prim算法——让一棵小树长大
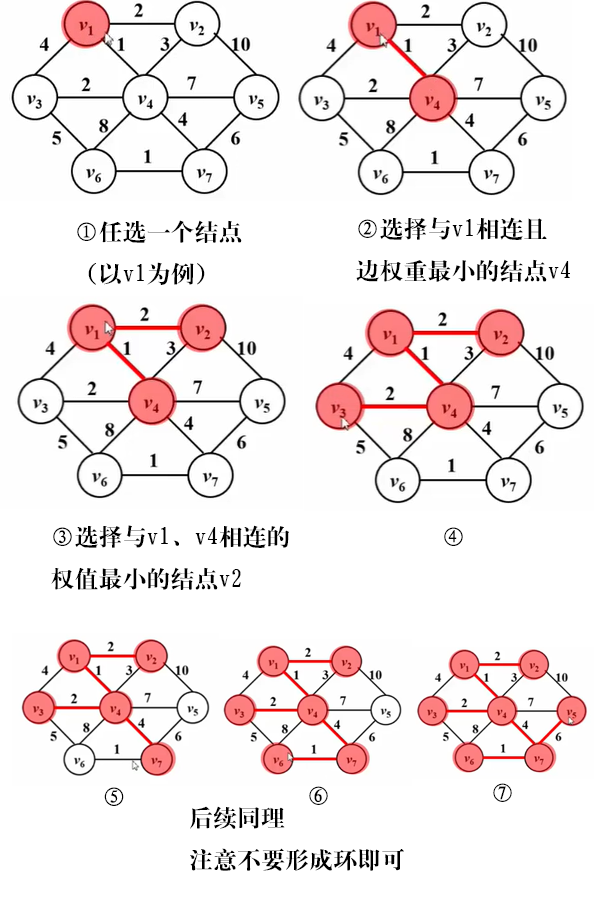
Prim算法有一点像Dijkstra算法
时间复杂度O(n²),因此Prim算法适合边稠密(点少)图。
(2)Kruskal算法——让许多小树合并
特点:相比Prim算法,是更直接了当的贪心(每次都直接选取最小权值边)
适用于:图比较稀疏(边少,可能差不多和结点数是同一数量级的)
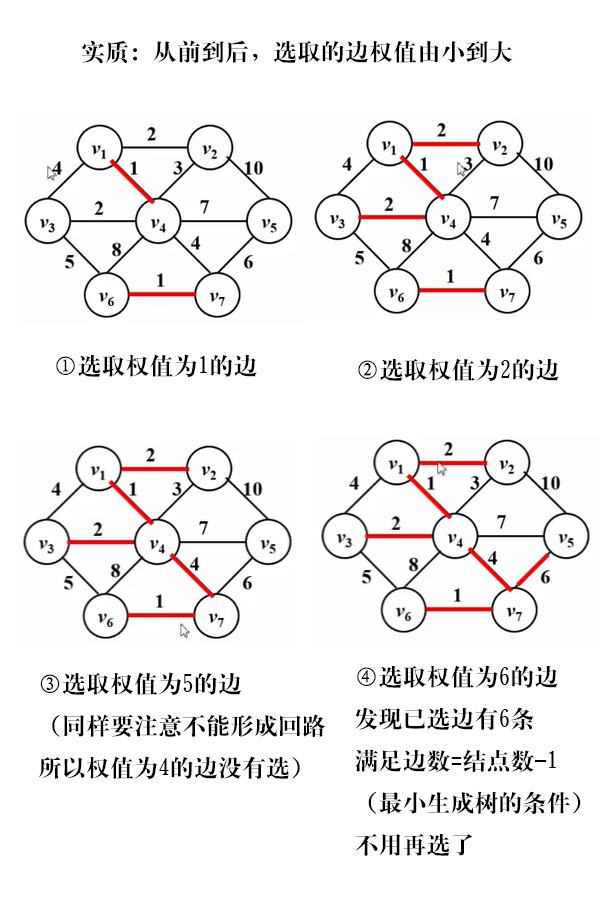
时间复杂度O(ElogE),因此Kruskal算法适合边稀疏图。
图的遍历
无向图的遍历
eg.
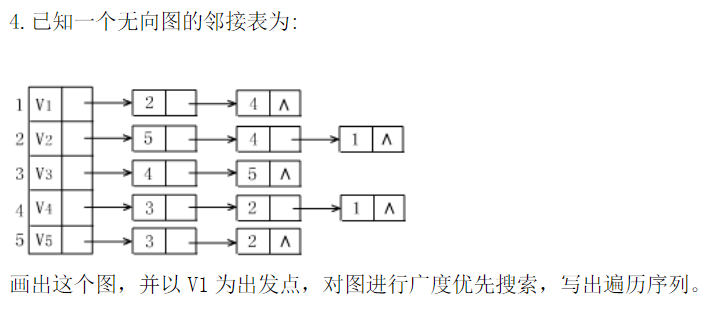
如何画邻接表的无向图?
参考:https://blog.csdn.net/dyw_666666/article/details/85232145
eg.
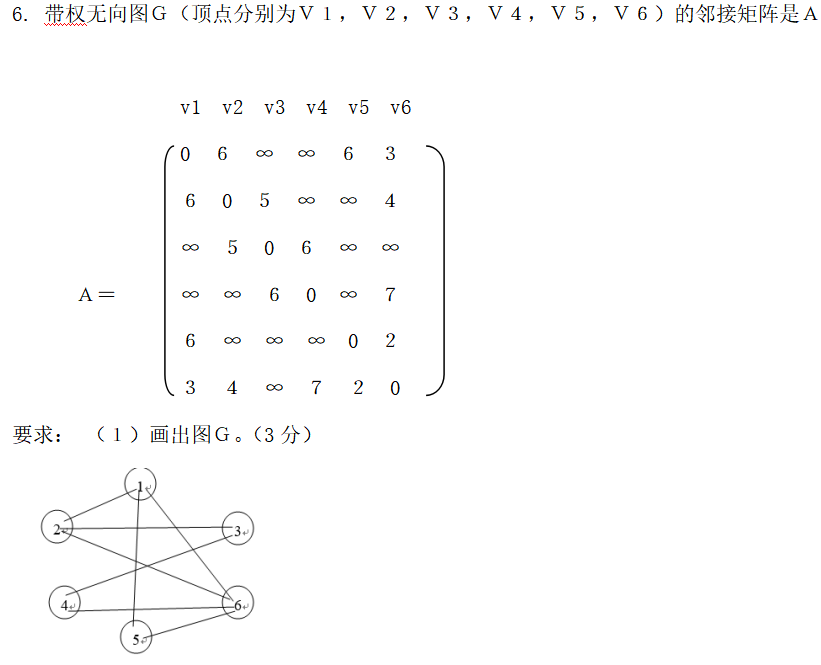
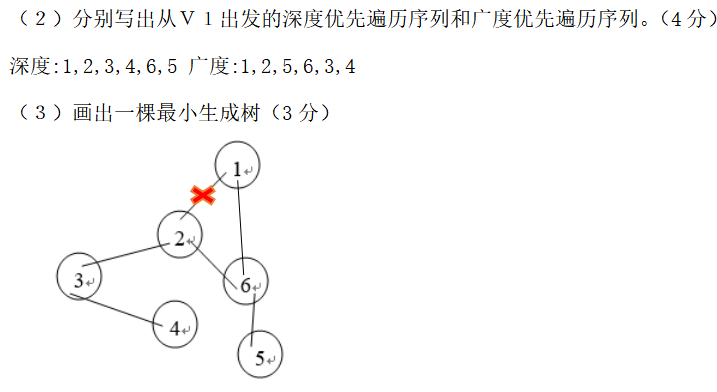
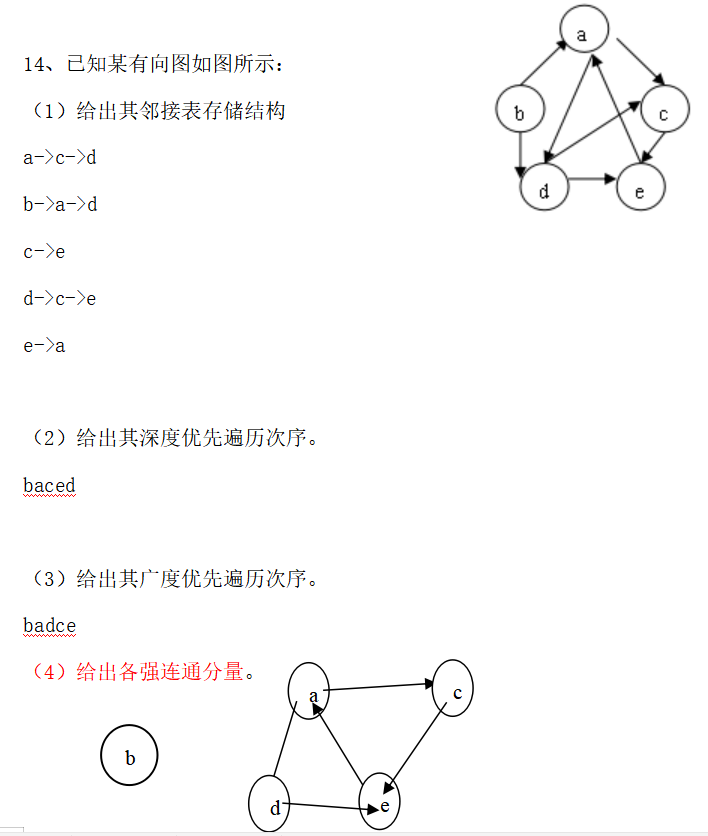
有向图的遍历


 浙公网安备 33010602011771号
浙公网安备 33010602011771号