【实战】客户流失数据分析
出自《Python数据分析基础》第7章 描述性统计与建模
使用统计图和摘要统计量对数据集进行探索和摘要分析,以及如何使用多元线性回归和逻辑斯蒂回归进行回归和分类分析。
一、环境
和链接博客第一章相同。
https://www.cnblogs.com/HarryMiau/p/19012307
二、数据集
客户流失数据集:https://github.com/albayraktaroglu/Datasets/blob/master/churn.csv
包含3333条观测文件,其中观测的是电信公司现有的和曾经的客户。
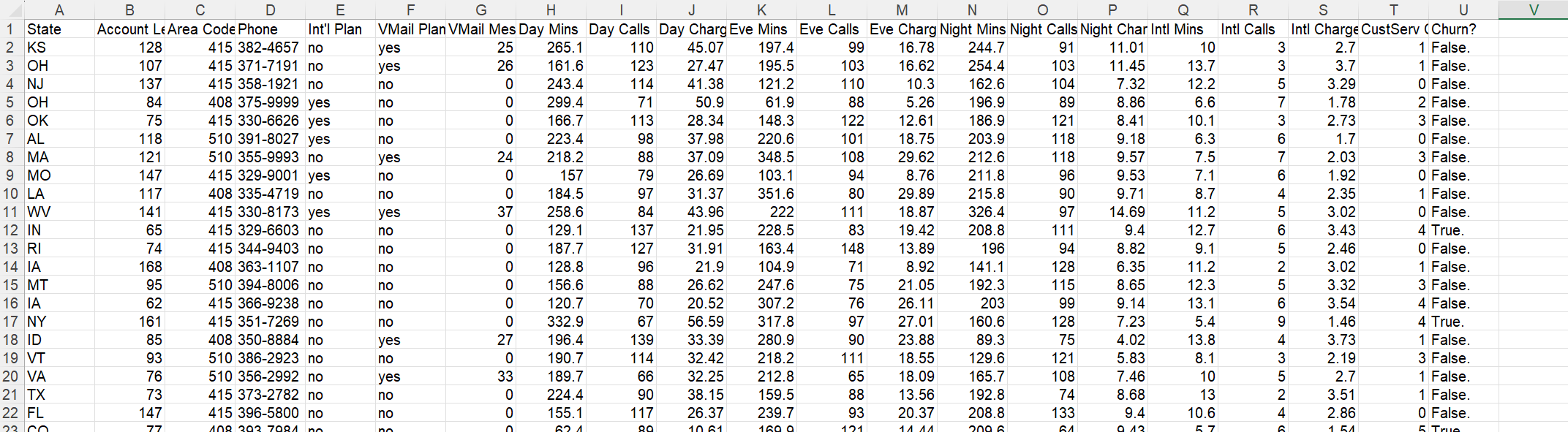
三、初步处理
导入库
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.formula.api import ols, glm
将数据集读入到pandas数据框中
# 1. 读取客户流失数据集
# 从CSV文件加载数据,使用第一行作为列名,逗号作为分隔符
churn_data = pd.read_csv(
'churn.csv', # 数据文件路径
sep=',', # 字段分隔符
header=0 # 用第1行作为列名
)
# 2. 标准化列名(清洗特殊字符,统一格式)
# 处理步骤:替换空格为下划线 → 移除单引号 → 去除首尾问号 → 转为小写
cleaned_columns = []
for original_column in churn_data.columns:
# 替换空格为下划线(避免列名中有空格)
col = original_column.replace(' ', '_')
# 移除单引号(处理包含英文单引号的列名)
col = col.replace("'", "")
# 去除列名首尾的问号(处理类似"churn?"的列名)
col = col.strip('?')
# 转为全小写(统一命名风格,避免大小写混淆)
col = col.lower()
cleaned_columns.append(col)
# 将清洗后的列名应用到数据集
churn_data.columns = cleaned_columns
# 3. 创建数值型流失标识列(方便后续建模)
# 将字符串类型的流失标识('True.'/'False.')转换为0/1数值
# 1表示流失,0表示未流失
churn_data['churn01'] = np.where(
churn_data['churn'] == 'True.', # 判断条件:如果churn列值为'True.'
1.0, # 满足条件时赋值1.0(流失)
0.0 # 不满足条件时赋值0.0(未流失)
)
# 4. 查看数据前5行,确认处理结果
print(churn_data.head())
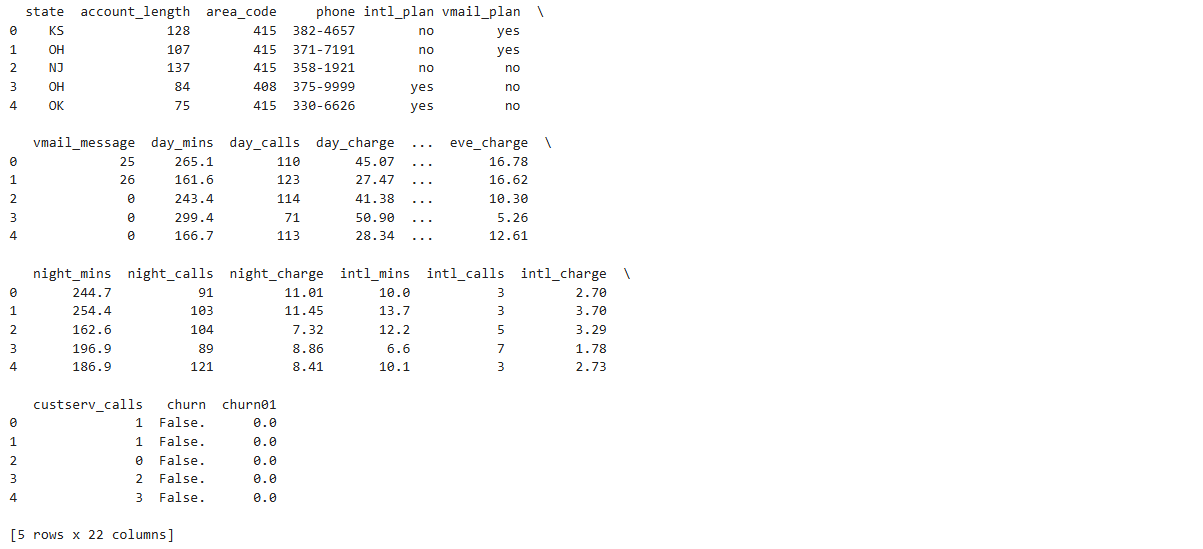
描述性统计量
按照 churn 这一列中的值将数据分成两组:已流失的客户和未流失的客户。
然后为每个分组中的一些特定的列计算 3 个统计量:总数、均值和标准差。
# 按流失状态(churn)分组,对指定列计算统计量
# 1. 按churn列分组
churn_groups = churn_data.groupby(['churn'])
# 2. 选择需要分析的列
columns_to_analyze = [
'day_charge', # 白天通话费用
'eve_charge', # 晚间通话费用
'night_charge', # 夜间通话费用
'intl_charge', # 国际通话费用
'account_length', # 账户时长
'custserv_calls' # 客服呼叫次数
]
grouped_columns = churn_groups[columns_to_analyze]
# 3. 计算指定的统计量
statistics_to_calculate = [
'count', # 样本数量
'mean', # 平均值
'std' # 标准差
]
churn_stats = grouped_columns.agg(statistics_to_calculate)
# 打印结果
print(churn_stats)
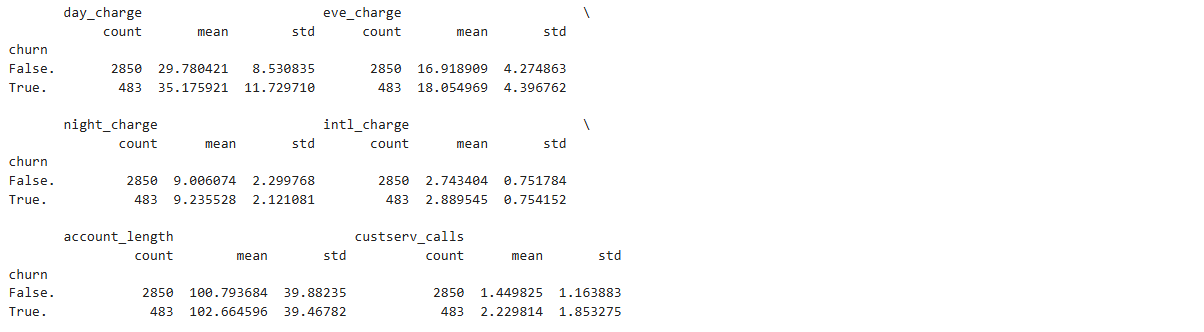
为不同的变量计算不同的统计量
# 定义需要聚合的列及其对应的聚合函数
aggregation_config = {
# 通话费用相关列:计算平均值和标准差
'day_charge': ['mean', 'std'],
'eve_charge': ['mean', 'std'],
'night_charge': ['mean', 'std'],
'intl_charge': ['mean', 'std'],
# 账户长度相关:计算数量、最小值和最大值
'account_length': ['count', 'min', 'max'],
# 客服呼叫相关:计算数量、最小值和最大值
'custserv_calls': ['count', 'min', 'max']
}
# 按churn分组并应用聚合配置
churn_aggregated = churn_data.groupby(['churn']).agg(aggregation_config)
# 打印结果
print(churn_aggregated)

按照新变量 total_charges 中的值使用等宽分箱法将数据分成 5 组,然后为每个分组计算 5 个统计量
# 创建总费用列
churn_data['total_charges'] = (
churn_data['day_charge'] +
churn_data['eve_charge'] +
churn_data['night_charge'] +
churn_data['intl_charge']
)
# 将总费用分为5组
factor_cut = pd.cut(churn_data['total_charges'], 5, precision=2)
# 定义统计量计算函数
def get_stats(group):
return {
'min': group.min(),
'max': group.max(),
'count': group.count(),
'mean': group.mean(),
'std': group.std()
}
# 按总费用分组并计算客服呼叫的统计量,添加observed=True消除警告
grouped = churn_data['custserv_calls'].groupby(factor_cut, observed=True)
# 应用统计函数并格式化输出
result = grouped.apply(get_stats).unstack()
print(result)

用 5 个统计量对客户服务通话数据进行摘要分析
# 将账户长度按照分位数进行分组(四分位数)
factor_qcut = pd.qcut(
x=churn_data['account_length'],
q=[0.0, 0.25, 0.5, 0.75, 1.0],
labels=['Q1 (0-25%)', 'Q2 (25-50%)', 'Q3 (50-75%)', 'Q4 (75-100%)'] # 增加标签提高可读性
)
# 按分位数分组,计算客服呼叫的统计量
# 添加observed=True避免FutureWarning
grouped = churn_data['custserv_calls'].groupby(factor_qcut, observed=True)
# 应用统计函数并格式化输出
stats_result = grouped.apply(get_stats).unstack()
# 打印结果
print(stats_result)

通过分位数对 account_length 进行划分,可以保证每个分组中包含数目大致相同的观测。
前一段代码中通过等宽分箱法得到的每个分组中包含的观测数目是不一样的。
qcut函数使用一个整数或一个分位数数组来设定分位数的数量,所以可以使用整数 4 来代替 [0., 0.25, 0.5, 0.75, 1.] 设定 4 等分,或使用 10 来设定 10 等分。
二值指标变量
# 为国际套餐和语音邮件套餐创建二值虚拟变量
# 使用drop_first=True避免多重共线性
intl_dummies = pd.get_dummies(
data=churn_data['intl_plan'],
prefix='intl_plan',
drop_first=True, # 移除第一个类别以避免虚拟变量陷阱
dtype=int # 明确指定为整数类型,更符合二值变量特性
)
vmail_dummies = pd.get_dummies(
data=churn_data['vmail_plan'],
prefix='vmail_plan',
drop_first=True,
dtype=int
)
# 将虚拟变量与churn列合并
churn_with_dummies = (
churn_data[['churn']]
.join([intl_dummies, vmail_dummies])
)
# 打印前5行查看结果
print(churn_with_dummies.head())

将一列按照四分位数进行划分,为每个四分位数创建二值指标变量
# 将总费用按四分位数分组并创建虚拟变量
# 定义四分位组名称
qcut_names = ['1st_quartile', '2nd_quartile', '3rd_quartile', '4th_quartile']
# 按四分位数划分总费用并添加标签
total_charges_quartiles = pd.qcut(
x=churn_data['total_charges'], # 明确指定数据列
q=4, # 分为4个四分位
labels=qcut_names, # 应用自定义标签
duplicates='drop' # 处理可能的重复区间问题
)
# 为分组结果创建二值虚拟变量
charge_dummies = pd.get_dummies(
data=total_charges_quartiles,
prefix='total_charges', # 虚拟变量前缀
dtype=int # 确保输出为整数类型(0/1)
)
# 将虚拟变量合并到原始数据框
churn_with_dummies = churn_data.join(charge_dummies)
# 查看合并后的数据前5行
print(churn_with_dummies.head())
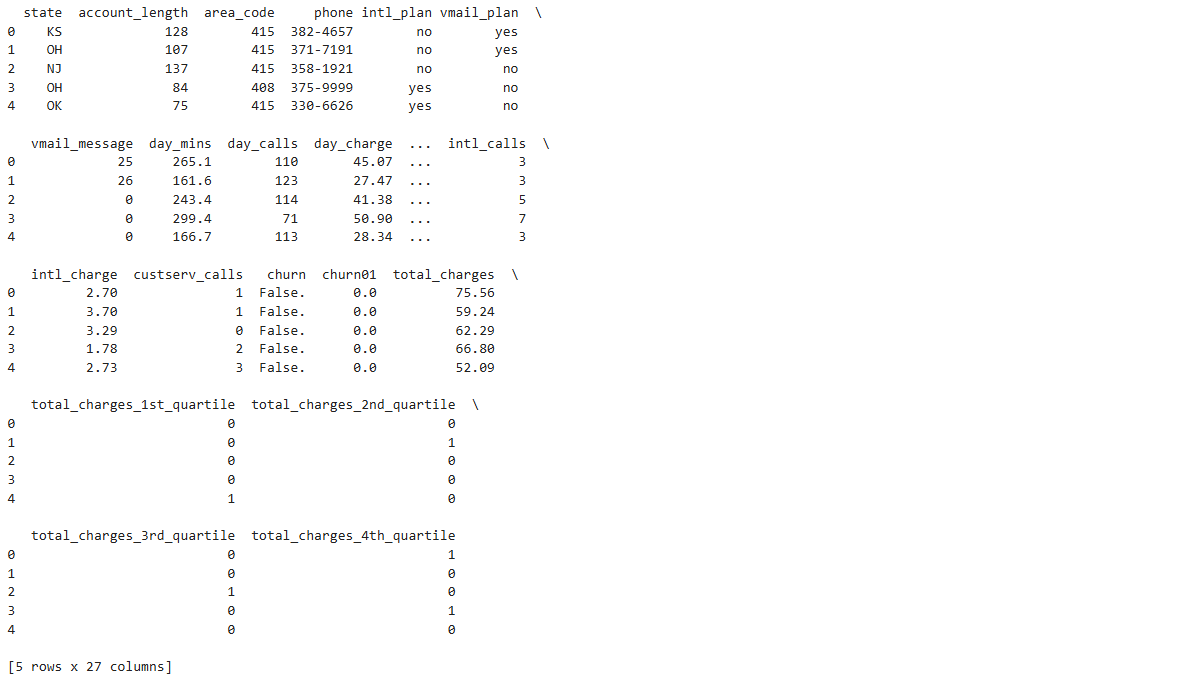
创建透视表
# 创建不同维度的透视表,分析总费用与客户流失、客服呼叫的关系
# 1. 按流失状态和客服呼叫次数分组的总费用透视表
pivot1 = churn_data.pivot_table(
values=['total_charges'],
index=['churn', 'custserv_calls']
)
print("按流失状态和客服呼叫次数分组的总费用统计:")
print(pivot1)
print("\n" + "-"*80 + "\n")
# 2. 按流失状态分组、客服呼叫次数为列的总费用透视表
pivot2 = churn_data.pivot_table(
values=['total_charges'],
index=['churn'],
columns=['custserv_calls']
)
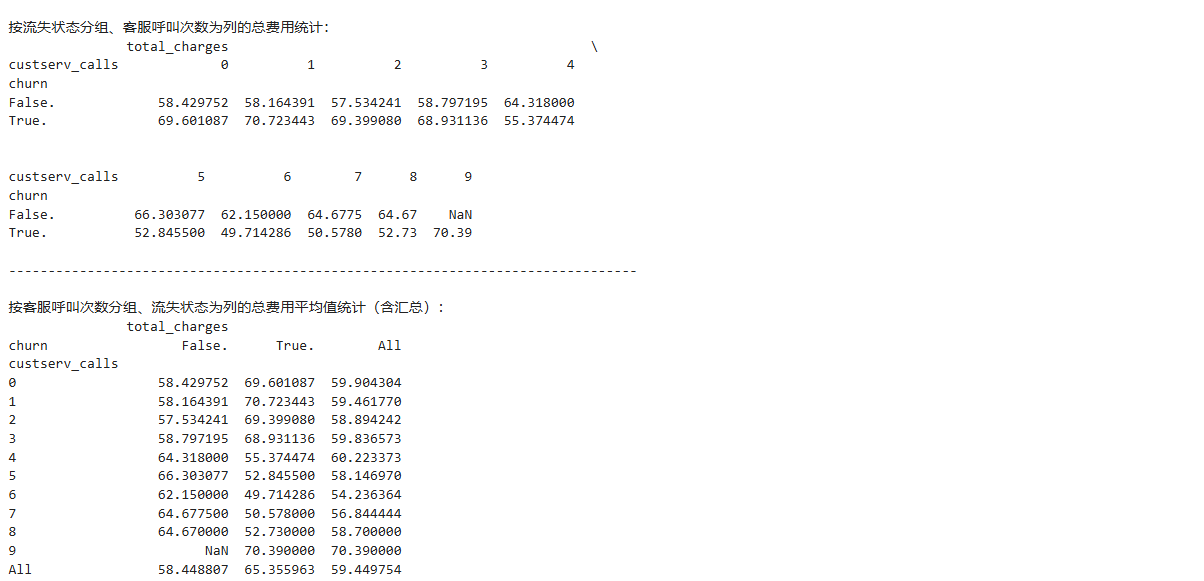
print("按流失状态分组、客服呼叫次数为列的总费用统计:")
print(pivot2)
print("\n" + "-"*80 + "\n")
# 3. 按客服呼叫次数分组、流失状态为列的总费用平均值透视表(含汇总)
pivot3 = churn_data.pivot_table(
values=['total_charges'],
index=['custserv_calls'],
columns=['churn'],
aggfunc='mean',
fill_value=pd.NA, # 使用pd.NA替代'NaN',更符合pandas的缺失值处理
margins=True
).infer_objects(copy=False) # 添加类型推断,消除警告
print("按客服呼叫次数分组、流失状态为列的总费用平均值统计(含汇总):")
print(pivot3)

四、逻辑斯蒂回归(Logistic Regression)
在这个数据集中,因变量是一个二值变量,表示客户是否已经流失并不再是公司客户。
线性回归不适合这种情况,因为它可能会生成小于 0 或大于 1 的预测结果,这在概率上是没有意义的。
因为因变量是一个二值变量,所以需要将预测值限制在 0 和 1 之间。
逻辑斯蒂回归可以满足这个要求。
# 定义因变量和自变量
dependent_variable = churn_data['churn01'] # 二分类目标变量(0/1)
# 选择用于建模的特征变量
independent_variables = churn_data[
['account_length', # 账户长度
'custserv_calls', # 客服呼叫次数
'total_charges' # 总费用
]
]
# 添加常数项(逻辑回归需要显式加入截距项)
independent_variables_with_constant = sm.add_constant(
independent_variables,
prepend=True # 常数项放在最前面
)
# 构建并拟合逻辑斯蒂回归模型
logit_model = sm.Logit(
dependent_variable,
independent_variables_with_constant
).fit()
# 输出模型详细摘要(包含系数、显著性等)
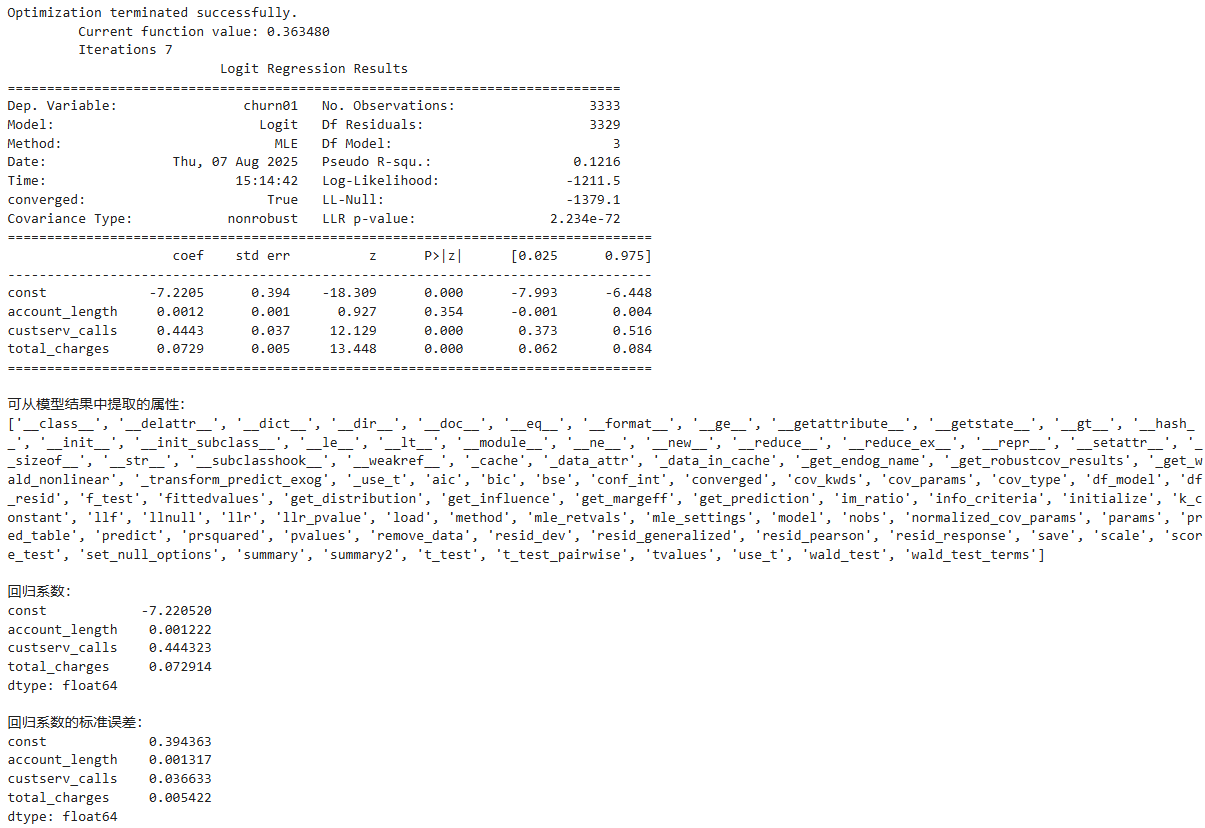
print(logit_model.summary())
# 展示模型结果可提取的属性
print("\n可从模型结果中提取的属性:")
print(dir(logit_model))
# 输出系数值
print("\n回归系数:")
print(logit_model.params)
# 输出系数的标准误差
print("\n回归系数的标准误差:")
print(logit_model.bse)
五、系数解释
对逻辑斯蒂回归系数的解释不像线性回归那么直观,因为逻辑斯蒂函数的反函数是条曲线,这说明自变量一个单位的变化所造成的因变量的变化不是一个常数。
因为逻辑斯蒂函数的反函数是一条曲线,所以必须选择使用哪个函数值来评价自变量对成功概率的影响。
和线性回归一样,截距系数的意义是当所有自变量为 0 时成功的概率。
有些时候 0 是没有意义的,所以另外一种方式是当自变量都取均值时,看看函数的值有何意义:
from math import exp
def inverse_logit(model_value):
"""计算逻辑斯蒂函数(Sigmoid函数),将线性结果转换为概率"""
return 1.0 / (1.0 + exp(-model_value))
# 计算所有自变量取均值时的线性预测值
# 使用iloc按位置访问参数,避免FutureWarning
at_means = (
logit_model.params.iloc[0] # 截距项(按位置访问第一个参数)
+ logit_model.params.iloc[1] * churn_data['account_length'].mean()
+ logit_model.params.iloc[2] * churn_data['custserv_calls'].mean()
+ logit_model.params.iloc[3] * churn_data['total_charges'].mean()
)
# 转换为概率并打印(保留两位小数)
print(f"所有自变量取均值时的流失概率:{inverse_logit(at_means):.2f}")

要计算某个自变量一个单位的变化造成的因变量的变化,可以通过计算当某个自变量从均值发生一个单位的变化时,成功概率发生了多大的变化。
例如,下面来计算一下当客户服务通话次数在均值的基础上发生一个单位的变化时,对客户流失概率造成的影响:
# 提取模型参数(使用iloc按位置访问,避免警告)
intercept = logit_model.params.iloc[0] # 截距项
coef_account_length = logit_model.params.iloc[1] # 账户长度系数
coef_custserv_calls = logit_model.params.iloc[2] # 客服呼叫系数
coef_total_charges = logit_model.params.iloc[3] # 总费用系数
# 计算各特征的均值
mean_account_length = churn_data['account_length'].mean()
mean_custserv_calls = churn_data['custserv_calls'].mean()
mean_total_charges = churn_data['total_charges'].mean()
# 计算客服呼叫次数为均值时的线性预测值
linear_pred_mean = (
intercept
+ coef_account_length * mean_account_length
+ coef_custserv_calls * mean_custserv_calls
+ coef_total_charges * mean_total_charges
)
# 计算客服呼叫次数减少1时的线性预测值
linear_pred_mean_minus_1 = (
intercept
+ coef_account_length * mean_account_length
+ coef_custserv_calls * (mean_custserv_calls - 1.0) # 客服呼叫次数减1
+ coef_total_charges * mean_total_charges
)
# 计算并打印客服呼叫次数变化1单位时的流失概率差异
prob_diff = inverse_logit(linear_pred_mean) - inverse_logit(linear_pred_mean_minus_1)
print(f"客服呼叫次数变化1单位时的流失概率差异:{prob_diff:.2f}")

第一段代码与计算 at_means 的代码相同。
第二段代码也与其基本相同,区别在于将客户服务通话次数的均值减去了 1。
最后一行代码打印出了两个逻辑斯蒂函数反函数值的差,其中一个是所有自变量为均值时的反函数值,另一个是两个自变量为均值,客户服务通话次数为均值减 1 时的反函数值。
在这个示例中,cust_serv_mean 的值与 at_means 相同,都是 -2.068。
cust_serv_mean_minus_one 的值是 -2.512。-2.068 的反函数值减去 -2.512 的反函数值的结果是 0.0372,
所以在均值附近减少一次客户服务通话就对应着客户流失概率提高 3.7 个百分点。
六、预测
仅出于方便和演示的目的,才使用这些已经用于拟合模型的数据。
除了这个示例之外,你应该使用未用于拟合模型的数据来评价模型,并用新的观测数据进行预测。
# 在churn数据集中
# 使用前10个观测创建10个“新”观测
new_observations = churn_data.loc[churn_data.index.isin(range(10)), independent_variables.columns]
new_observations_with_constant = sm.add_constant(new_observations, prepend=True)
# 基于新观测的账户特性
# 预测客户流失可能性
y_predicted = logit_model.predict(new_observations_with_constant)
# 将预测结果保留两位小数并打印到屏幕上
y_predicted_rounded = [round(score, 2) for score in y_predicted]
print(y_predicted_rounded)

参考资料
[1] [美]克林顿 W. 布朗利 (Clinton W. Brownley). Python数据分析基础[M]. 陈光欣,译. 北京:人民邮电出版社,2017:192-208.
[2] 【实战】葡萄酒质量数据分析


 浙公网安备 33010602011771号
浙公网安备 33010602011771号